水声语音通信在国防建设、海洋资源开发、科考、搜救等领域中有着很广泛的应用。采用模拟单边带调制技术的水声通信设备如美国 AN/WQC-2A 水声通信机[1]受海洋水声环境的影响很大,特别是水声信号幅度易受水声信道幅度衰落特性影响,使得单边带调制语音通信质量难以保证[1-2]。
数字语音通信系统可利用相干调制、语言编码、信道匹配与均衡技术提高性能[3]。英国拉夫堡大学采用数字脉冲位置调制技术(Digital Pulse Position Modulation,DPPM)实现语音通信[4]。殷敬伟等[5]设计了时域差分正交频分复用技术(Orthogonal Frequency Division Multiplexing,OFDM)水下语音通信系统。周跃海等[6]基于时反结合时频差分 OFDM 语音通信体制设计了水声语音通信系统。但在浅海水声信道条件下,数字语音通信方法易受到载频误差、多普勒频移、相位噪声、同步丢失等影响导致性能严重下降,在高误码率情况下甚至导致语音完全损失。
调频水声语音通信系统在调频调制过程中由于非线性调制造成了信号频谱结构中具有新的边频分量且在有效调制带宽两侧成对称分布[7];同时,在解调过程中由于频率捕获效应的存在,可利用强信号对弱信号的抑制作用[8]来提高抗干扰能力。但是,浅海水声信道具有的复杂多径效应及噪声将严重影响调频水声语音获得的语音音质,特别是在较为明显的多径干扰下会出现解调语音含混、语义难辨等问题。
非线性解调[7]和正交解调[9]是 2 种常用的调频解调方法:非线性解调直接使用非线性模拟电路对调制信号进行实时解调,无需进行数字处理。正交解调法则是一种不涉及希尔伯特变换和反正切运算的数字化解调方法,实现简单方便[9]。这 2 种调频解调方法在水声语音通信中均得到一定的应用,曾堃[10]采用了非线性解调方法设计了调频水声语音实时通信系统,卜文强[11]采用了正交解调法设计了水声语音通信系统。但目前未见不同的浅海水声信道特性(多径、信噪比)对 2 种方法获得的语音质量的影响比较。本文对采用非线性解调和正交解调的调频水声语音通信系统进行浅海信道条件下的性能评估和量化比较。
传统水声通信系统可采用语音信噪比、误比特率等指标进行接收语音的性能评估,但考虑到水声调频语音通信系统目的在于获得语义可懂的接收语音,因此语音通信质量是更为重要的一个性能指标。语音质量评价方法可分为主观评价和客观评价。主观语音评价方法可以得到较准确的结果,但是评估过程费时费力,容易受测试条件限制和测试人员主观因素影响,不适用于水声实时通信系统。PESQ 是一种采用改进型认知模型技术和听觉模型技术的语音质量客观评价算法[12]。由于充分考虑端到端的网络时延,它对通信延时、环境噪声等有较好的鲁棒性[13],所以本文采用 PESQ 算法对采用非线性解调和正交解调的水声调频语音通信系统进行性能评估和量化比较。
1 调频水声通信方法 1.1 调制调频调制[14]信号的一般表达式为:
| $ {S_m}\left( t \right) = A{\rm{cos}}\left[ {{\omega _c}t + \varphi \left( t \right)} \right]\text{。} $ | (1) |
式中:A 为载波的振幅;
调频调制是指瞬时频率偏移随着调制信号m(t)成比例变化,即:
| $ \frac{{{\rm{d}}\varphi \left( t \right)}}{{{\rm{d}}t}} = {K_f}m\left( t \right)\text{,} $ | (2) |
式中Kf 为调制灵敏度,rad/(s·V)。这时相位偏移为:
| $ \varphi \left( t \right) = {K_f}\int {^m\left( \tau \right){\rm{d}}\tau } \text{,} $ | (3) |
代入式(1),可得调频信号为:
| $ {S_{FM}}\left( t \right) = A{\rm{cos}}\left[ {{\omega _c}t + {K_f}\int {^m\left( t \right){\rm{d}}\tau } } \right]\text{。} $ | (4) |
设调制信号为单一频率的正弦波,即:
| $ m\left( t \right) = {A_m}{\rm{cos}}\left( {{\omega _m}t} \right)\text{。} $ | (5) |
当它对载波进行调频调制时,由式(4)可得出调频信号:
| $ \begin{array}{l} {S_{FM}}\left( t \right) = A{\rm{cos}}\left[ {{\omega _c}t + {K_f}{A_m}\mathop \smallint \nolimits^ cos\left( {{\omega _m}\tau } \right){\rm{d}}\tau } \right]=\\[5pt] \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; A{\rm{cos}}\left[ {{\omega _c}t + {m_f}{\rm{sin}}\left( {{\omega _m}t} \right)} \right]\text{。} \end{array} $ | (6) |
式中mf 为调频指数。
| $ {m_f} = \frac{{{K_f}{A_m}}}{{{\omega _m}}}\text{。} $ | (7) |
由式(7)可得,对于单音频波调制指数mf 反比于调制角频率ωm。
1.2 非线性解调非线性解调是直接用非线性模拟解调电路对接收到的调制信号进行解调。非线性解调器通常由限幅器、带通滤波器、包络检波电路和抽样判决器组成[11]。非线性解调流程图如图 1 所示。

|
图 1 非线性解调流程图[10] Fig. 1 The process of nonlinear demodulation method |
考虑到水声信道的幅度衰落对调频水声语音通信系统造成的影响,通常需要对接收信号进行限幅和放大的处理后再进行解调,以抑制幅度衰落带来的干扰[11]。
1.3 正交解调假设调频接收端信号的表达式为[12]:
| $ S\left( t \right) = {A_c}\left( t \right){\rm{cos}}\left[ {{\omega _c}t + {K_f}\mathop \smallint \limits_{-\infty }^t m\left( \tau \right){\rm{d}}\tau } \right]\text{。} $ | (8) |
其中,Ac(t)表示受到信道噪声、多径等其他干扰影响后随时间变化的调频信号幅度,m(t)为调制信号。将式(8)与本地产生的正交载波信号相乘,可得到以下结果:
| $ \begin{split} \\[-12pt] {S_1}\left( t \right) =& S\left( t \right) \times \cos \left( {{\omega _c}t} \right)=\\ & {A_c}\left( t \right) \times \frac{1}{2}\left\{ {\cos \left[ {2{\omega _c}t + {K_f}\mathop \smallint \limits_{-\infty }^t m\left( \tau \right){\rm{d}}\tau } \right]} \right. + \\ & \left. {\cos \left[ {{K_f}\mathop \smallint \limits_{-\infty }^t m\left( \tau \right){\rm{d}}\tau } \right]} \right\}\text{,} \end{split} $ | (9) |
| $ \begin{split} \\[-12pt] {S_2}\left( t \right) =& S\left( t \right) \times \sin \left( {{\omega _c}t} \right) = \\ & {A_c}\left( t \right) \times \frac{1}{2}\left\{ {\sin \left[ {2{\omega _c}t + {K_f}\mathop \smallint \limits_{-\infty }^t m\left( \tau \right){\rm{d}}\tau } \right]} \right.-\\ & \left. {\sin \left[ {{K_f}\mathop \smallint \limits_{-\infty }^t m\left( \tau \right){\rm{d}}+ \tau } \right]} \right\}\text{。} \end{split} $ | (10) |
对S1(t),S2(t)分别进行低通滤波处理后,得到:
| $ I\left( t \right) = {A_c}\left( t \right)\cos \left[ {{K_f}\mathop \smallint \limits_{-\infty }^t m\left( \tau \right){\rm{d}}\tau } \right]\text{,} $ | (11) |
| $ Q\left( t \right) =-{A_c}\left( t \right)\sin \left[ {{K_f}\mathop \smallint \limits_{-\infty }^t m\left( \tau \right){\rm{d}}\tau } \right]\text{,} $ | (12) |
由式(11)和式(12)可得:
| $ \begin{split} \\[-12pt] I'\left( t \right)& Q\left( t \right)-I\left( t \right)Q'\left( t \right) = \Bigg\{ {{{\sin }^2}} \Bigg[ {{K_f}\int_{-\infty }^t {m\left( \tau \right){\rm{d}}\tau } }\Bigg ] + \\ & {{{\cos }^2}\Bigg[ {{K_f}\int_{-\infty }^t {m\left( \tau \right){\rm{d}}\tau } } \Bigg]} \Bigg\} \times A_c^2\left( t \right) \times {K_f} \times m\left( t \right)\text{。} \end{split} $ | (13) |
观察式(11)~式(13),可以推出解调信号m(t)的表达式为:
| $ m\left( t \right) = \frac{{I'\left( t \right)Q\left( t \right)-I\left( t \right)Q'\left( t \right)}}{{\left[ {{I^2}\left( t \right) + {Q^2}\left( t \right)} \right] \times {K_f}}}\text{。} $ | (14) |
从正交解调法可看出,水声信道引入的幅度衰落可通过正交及低通滤波处理进行抑制。正交解调原理框图如图 2 所示。
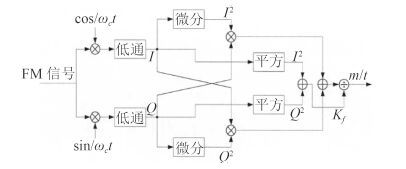
|
图 2 正交解调原理框图 Fig. 2 The process of orthogonal demodulation method |
为了对上述 2 种调频水声语音通信系统的性能进行评估,在厦门五缘湾海域进行了海试实验。原始语音采样率 4 ksps,语音内容为男声“厦门大学正在进行语音测试”,调频调制参数如表 1 所示。在接收端,非线性解调器由前置放大、带通滤波、限幅器、包络检波电路和抽样判决器组成;正交解调器对前置放大、带通滤波后的接收信号进行模数转换后在 PC 中离线处理,模数转换采样率为 192 ksps。在实验中,2 种解调器的接收信号经过相同的前置放大、带通滤波电路,以方便评估解调方法性能。
|
|
表 1 调频系统的参数设置 Tab.1 The parameters of FM system |
在实验海域不同收发距离、接收深度的 3 种信道中对 2 种调频水声语音通信系统进行性能测试和比较评估。信道 1 收发距离为 100 m,发射深度 2 m,接收深度 2 m,信道 2 收发距离 1 km,发射深度 2 m,接收深度 6 m,信道 3 收发距离 1 km,发射深度 2 m,接收深度 1 m。
图 3 为实验海域声速梯度曲线图,图 4(a)~图 4(c)分别为实验水声信道 1,2,3 的信道响应图。从图 4 可看到,实验水域浅海水声信道存在明显的多径,其中信道 1 存在 2 条可分辨的相邻多径,信道 2 有多条相近的多径形成复杂的混叠多径结构,信道 3 则有一个较为明显的主径。
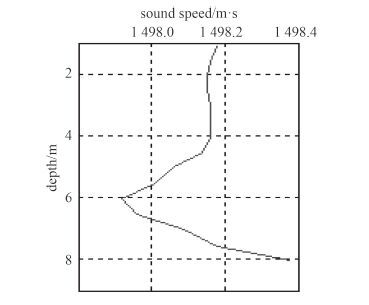
|
图 3 声速梯度 Fig. 3 Sound speed gradient |

|
图 4 实验水声信道特性图 Fig. 4 Response of experimental underwater acoustic channels |
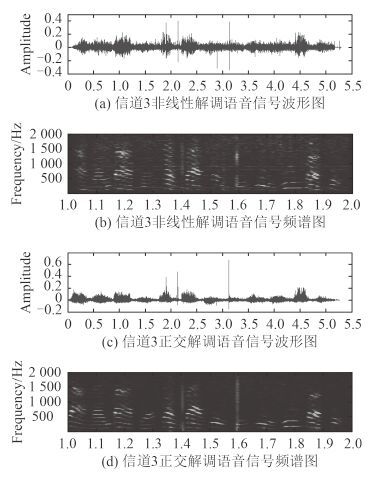
调频水声语音通信的原始语音信号波形图和频谱图如图 5 所示,解调结果如图 6、图 7 和图 8 所示。其中,图 6(a)~图 6(b)和图 6(c)~图 6(d)分别为信道 1 的调频水声语音通信系统的非线性解调法和正交解调法解调输出信号波形图、频谱图;图 7(a)~图 7(b)和图 7(c)~图 7(d)分别为信道 2 的调频水声语音通信系统的非线性解调法和正交解调法解调输出信号波形图、频谱图;图 8(a)~图 8(b)和图 8(c)~图 8(d)分别为信道 3 的调频水声语音通信系统的非线性解调法和正交解调法解调输出信号波形图、频谱图。由于浅海信道存在明显的多径效应,从语音波形图和频谱图可看出,解调后的语音信号存在着明显的噪声干扰和频散现象,这在一定程度上影响了调频水声语音通信系统的解调语音质量,降低了语音通信性能。其中,由于信道 2 具有较为复杂的混叠多径结构,其获得的解调语音频散现象尤为明显。同时对比 2 种解调方法得到的语音信号的波形频谱图,可以发现正交解调法在解调过程中对底噪的抑制优于非线性解调法。

|
图 5 原始语音信号波形频谱图 Fig. 5 The waveform and specetrogram of original speech |
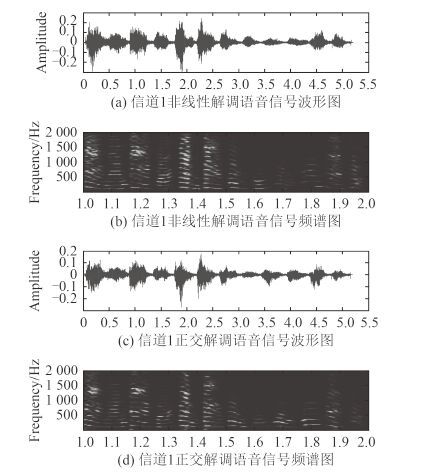
|
图 6 语音波形频谱图(信道 1) Fig. 6 The waveform and spectrogram of speech from channel 1 |
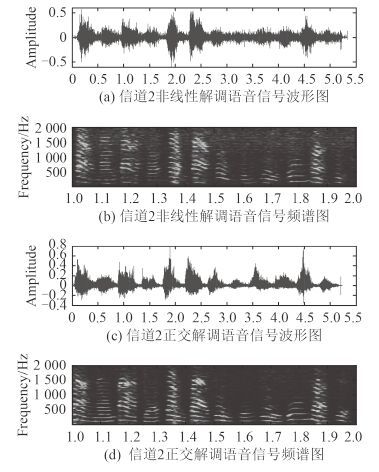
|
图 7 语音波形频谱图(信道 2) Fig. 7 The waveform and spectrogram of speech from channel 2 |
|
图 8 语音波形频谱图(信道 3) Fig. 8 The waveform and spectrogram of speech from channel 3 |
PESQ 语音质量客观评价方法的满分为 4.50,得分越高说明语音质量越好。通过 PESQ 语音质量客观评价方法对 2 种不同调频水声语音通信系统的解调语音信号评估结果如表 2 所示。从表 2 可看出,信道 1 和信道 2 的接收信噪比较高,信道 3 的接收信噪比最低,在信噪比较高的信道 1 和信道 2 中,非线性解调法的解调语音质量优于正交解调法的解调语音质量;而在信噪比较低的信道 3 中,正交解调法的解调语音质量优于非线性解调法的解调语音质量。实验结果反映出正交解调法对较低的接收信噪比具有较好的鲁棒性。
|
|
表 2 解调语音信号 PESQ 评估结果 Tab.2 PESQ evaluation results of the demodulated speech signal |
结合信道特性图和解调信号频谱图可以发现:对于多径影响程度不同的信道,非线性解调法获得的解调语音质量较为稳定,如在具有较为复杂的混叠多径结构信道 2 中,正交解调法获得的解调语音质量出现明显下降。实验结果反映出非线性解调法对信道的多径干扰具有较好的鲁棒性。
3 结语本文对水声语音通信系统的非线性解调法的和正交解调法进行性能评估和量化比较,浅海信道条件下的语音通信实验结果表明,从语音音质 PESQ 量化评估的角度,非线性解调法受信道严重多径的影响较小,正交解调法则在较低接收信噪比下具有较好的语音解调性能。由于实验海区、实验次数尚不具有广泛性,本文获取的性能评估比较结果仅为初步结论,旨在为类似条件下的水声通信系统设计提供一定的参考。
| [1] | DANIEL B. KILFOYLE, ARTHUR B. Baggeroer. The state of art in underwater acoustic telemetry, IEEE J. Oceanic. Eng, 25(1):4-27, 2000, 25:4-27. |
| [2] | PROAKIS J G, SOZER E M, RICE J A. "Communications magazing", IEEE, 2011, 39(11). |
| [3] | 郭中源, 陈岩, 贾宁, 等. 水下数字语音通信系统的设计和实现[J]. 声学学报, 2008, 33 (5):409–418. |
| [4] | SARI H, WOODWARD B. Underwater acoustic voice communications using digital pulse position modulation. proc. Oceans'98. |
| [5] | 殷敬伟, 王驰, 白夜, 等. 基于正交频分复用的水下语音通信应用研究[J]. 兵工学报, 2013, 34 (5):593–596. |
| [6] | 周跃海, 江伟华, 陈磊, 等. 采用时反和时频差分OFDM的水声语音通信方法[J]. 应用声学, 2015 (4):283–290. |
| [7] | 曾晓珊. 基于模式调频的水声通信方法[D].广州:华南理工大学, 2012. http://cn.bing.com/academic/profile?id=a12a8bd224b13ad34cdbbc17fa72a045&encoded=0&v=paper_preview&mkt=zh-cn |
| [8] | 王洪亮. 频率捕获效应在民航通信导航系统中的应用[J]. 黑龙江科技信息, 2012 (35). |
| [9] | 祝林啸, 吴嗣亮. 一种调频信号数字正交解调方法[J]. 电讯技术, 2005 (4). |
| [10] | 曾堃. 多径信道下的调频水声语音通信技术研究[D]. 厦门:厦门大学. 2015. |
| [11] | 卜文强. 基于TMS320C67X的水声语音通信系统研究与实现[D]. 厦门:厦门大学. 2014 |
| [12] | 黄绍. 基于PESQ估测模型的水声语音通信系统研究[D]. 厦门:厦门大学, 2013. |
| [13] | QIAO Z, SUN L, IFEACHOR E. Case study of PESQ performance in live wireless mobile VoIP environment[C]//. Personal, Indoor and Mobile Radio Communications, 2008. PIMRC 2008. IEEE 19th International Symposium on. IEEE, 2008:1-6. |
| [14] | 樊昌信. 通信原理教程[M]. 北京: 电子工业出版社, 2007. |
 2017, Vol. 39
2017, Vol. 39
