近年来,舰船用液压起重机的稳定控制问题,已成为舰船科学中的最主要研究问题,其应用于船舶结构工程、船舶水力工程、船舶设计工程与电子工程等众多领域中[1]。其中,在其应用于船舶机械中自动控制系统时,首先需要调节不同多个控制变量,如变压器档位灯、发电机端的电压控制和并联电路时的电流控制,变量调节完成后,为了保证控制过程的稳定性和可靠性,还需采用多目标优化算法,寻求船舶稳定控制的最优解。
但是,在一些机械设备的工作环境中,船舶的风浪给机械设备的控制过程带来较大问题。控制过程的多目标优化问题,是目前实现波浪补偿消摆控制的关键问题。由于其多目标优化求解过程较为繁琐,且解集往往存在不连续且分布不均匀等问题,因此难度远高于单目标优化[2]。在优化的过程中,考虑到控制解集的真实性,为实现解集尽可能的接近真实解,专家学者已将研究目标转移到快速且高效的多目标优化算法上[3-4]。
根据实际需求可知,控制器输出端必须满足不同海域风量条件下的目标动态最优,也就是所需解决波浪补偿消摆控制多目标优化问题[5]。考虑到船舶机械工程实际应用与需要,由于控制器输出端的各供电量互不相同,导致求解容易出现分布不均匀的情况,加大了多目标优化的难度[6]。在传统的船舶起重机设备中,一般采用机械的数学规划法,将多目标优化问题转化为单目标优化问题,然后采用加权的方式对其求解,但这种方法只对选取的单目标有积极作用[7],对其他目标的优化求解性能极其不理想;而且,若所需优化多目标的分布并不均匀,则传统方法无法对其实施求解过程,不能有效地求出并确定优化解集,得到的优化结果不均匀,且与真实解集之间偏差过大,不符合当今船舶机械工程实践中工程质量的要求,达不到多目标优化效率及质量[8-10]。
因此,针对传统方法存在的以上问题,为了实现快速高效地控制舰船液压起重机波浪补偿消摆,使控制优化解集更加接近真实解,本文提出一种小区域分区进化算法,来解决舰船液压起重机波浪补偿消摆控制问题。在控制算法中引入排挤因子,利用控制数据中的相互约束作用,形成小的控制单元,以此来维持控制过程的快速性,保证控制精度。实验表明,这种方法能够有效解决舰船液压起重机波浪补偿消摆控制问题,保证了船舶机械自动控制的准确性。
1 舰船液压起重机波浪补偿消摆控制的目标函 数设计在舰船液压起重机的动态控制系统中,不同控制站点之间并非毫无联系,当水流发生不同程度的颠波时,会对控制过程造成一定影响,时间与颠簸程度之间的非线性致使产生的影响也是非线性的,海洋颠簸环境对控制过程产生的影响,会随着控制系统的运行过程不断加大,由于两者之间的这种紧密的关系,使得运作流程都会受到影响。如今,现有的舰船液压起重机的动态控制系统,不能精准的表达出摆动与风浪强度之间的关系,所以舰船液压起重机的动态控制系统的多目标优化效率普遍偏低。利用不同设备之间的非线性关系,对舰船液压起重机各个部分之间的相互作用组建方程,对其进行表述,用这个方法来确保控制系统运行的稳定,提高其精准度。
现假设在此舰船液压起重机稳定控制系统中的相关设备的个数为n 个,在任意时间点或任意的时间段内,波浪对船舶稳定性的影响,是从一侧冲击发起,另一侧冲击结束,这一过程水的流量并不发生变化,把设备之间相互影响的关系组建成一个非线性方程。设第i 个站点的水流经量用Qi 表示,其它设备冲击此设备的水流量用ri 表示,冲击舰船液压起重机的水流量用qij 表示,用pij 表示不同的设备之间压力。根据舰船液压起重机两侧的水流量相等,且不发生变化,则不同设备的水流量与系统管道之间的影响关系如式(1)表示:
| $ \sum {{r_i}{\beta _i}} = \sum\limits_{i = 1}^n {{Q_i}} \text{,} $ | (1) |
对液压起重机与风浪强度之间的关系进行分析研究,可对其组建非线性方程:
| $ {r_i}-\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{p_{ij}}} } {\mathop{\rm sgn}} ({q_{ij}}-{q_{ji}})|{q_{ij}}-{q_{ji}}| = {Q_i}\text{,} $ | (2) |
如式(1)所示,将影响函数G(i,j)表述成非线性方程,完成相互之间影响的准确表述。
根据上述过程,完成了设备与风浪之间相互作用的表述,可得到模型的限制范围,对系统的控制进一步优化,式(3)为其优化目标函数:
| $ \left\{ {\begin{array}{*{20}{l}} {P = \alpha \sum\limits_{i = 1}^n {{p_i}{u_i}\beta } }\text{,}\\ {{u_i}-{Q_i}-\sum {{s_{ij}}{\mathop{\rm sgn}} ({p_i}-{p_j})|{p_i}-{p_j}{|^{1/\alpha }} = 0} }\text{,}\\[3pt] {\min \sum {{C_{ij}}({p_i}-{p_j}){Q_i} = 0} }\text{,}\\[3pt] {{r_i}-\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{p_{ij}}{\mathop{\rm sgn}} ({q_{ij}}-{q_{ji}})|{q_{ij}}-{q_{ji}}| = {Q_i}} } }\text{。} \end{array}} \right. $ | (3) |
式中,β 为两个相反的状态,当β = 0 时表示站点关闭,当β = 1 表示风浪冲击模式开启。α 是换算系数。
2 小区域分区进化算法在舰船液压起重机波浪 补偿消摆控制中的应用小区域分区进化方法不同于传统算法对多目标问题的求解过程,其通过一些分区来实现集合的完美分布,进而优化求解多目标,以下是此实现此过程的具体步骤。
2.1 小区域分区进化方法的提出小区域分区进化方法的核心是在一个固定特有的相同自然环境里衍生而来的,成员为了能够长久的活下来,他们就通过激烈竞争以得到生存所必要的东西,小区域分区进化方法使用先进拥挤方法,令其他的个体成员的必要条件都演变成自己的生存环境,利用该方法增强自己生存能力。该方法的首要任务就是假设各个个体i,在某个目的函数条件下的适应度用d 来描述,而且代表第i 个个体的小区域分区进化的个数,相关值也代表个体i 的集合程度。值的具体计算公式为:
| $ {m_i} = \sum\limits_{j \in Pop} {sh[d(i,j)]} \text{,} $ | (4) |
式中,Pop 为整个群体;d(i,j)为第i 个个体与第j 个个体所形成的距离,同样可以描述为彼此的相近度。除此之外,sh[d] 函数的表示成:
| $ sh[d] = \left\{ {\begin{array}{*{20}{c}} 0 \text{,}& {d > \sigma }\text{;}\\ {1-d/\sigma } \text{,}& {d < \sigma }\text{。} \end{array}} \right. $ | (5) |
式中,σ 为小区域分区进化的面积,其公式表示为:
| $ \sigma = (1/(\alpha \sqrt {2\pi } )){e^{-{f_i}^2/2{\alpha ^2}}}\text{。} $ | (6) |
式中:为解集分布度函数的标准方差,它的值与变化速度是反比例关系,依据值的大小来掌握彼此之间的影响程度。也就是将数字变小,它对适应程度的影响较大,进一步就确保个体的密度值能够体现解集实际的分布均匀状况。若将其变成比较大的数值,则其值就会立即改变适应度,导致解集彼此之间的关联不大,不会出现缓慢过度的情况,所以说,这个值直接决定着解集的分散均匀性与紧密程度,因此可以利用小区域分区进化方法产生个体环境,同时采用恰当的值,就能确保其非均匀性。
2.2 算法在舰船液压起重机波浪补偿消摆控制中的应用为了解决舰船液压起重机波浪补偿消摆控制多目标优化难题,解集不均匀、不是整体的问题,在整体分布比较好的情况下,小区域分区进化方法可以很好的解决这个问题。传统方法缺点就是不能将其当作完整的个体,造成分布性较差。小区域分区进化方法就是确保解集的分布程度好,将其变成尽可能多的小区域,进而达到解集的分散效果。
利用构造集的调配手段来建立舰船液压起重机波浪补偿消摆控制中小区域网格,采用回溯方法调配个体。舰船液压起重机波浪补偿消摆控制中,小区域集合的产生的具体步骤如下:
在M 中抽取一个控制单元,单个个体保证不唯一特性,假设M =M-{i},随后设定最开始的一个空集合C,初始化成为C =ϕ;
在舰船液压起重机波浪补偿消摆整体中控制中,在集合M 里随机选取一个控制单元个体j,也就是对比当前舰船液压起重机消摆状态j 与原来的状态i,若i >j,则取后一个体j,把它添加到新的需要控制的单元C 里,此公式表示为:
| $ C = (1/(\alpha \sqrt {2\pi } )){e^{-{f_i}^2/2{\alpha ^2}}}\text{。} $ | (7) |
把上述的新集合C 融入到舰船液压起重机波浪补偿消摆控制集合M 中,也就是M =M-C,之后找一个液压起重机控制状态k,并假定k >i 把结果添加到集合N 里,表示为:
| $ N = N \cup \{ i\} \text{。} $ | (8) |
根据以上的方法连续迭代进行步骤 2 到步骤 4 的操作,并对其判断,若舰船液压起重机波浪补偿消摆控制集合M 是空的,那么就不再执行操作。
对网格集合迭代算法后,依旧使用进化算法优化目标函数解集,算法为:
| $ h({f_i},M) = \left\{ {\begin{array}{*{20}{c}} {1-{{\left( {\frac{{{f_i}}}{{Mg}}} \right)}^\alpha }} \text{,}& {{f_i} \leqslant Mg}\text{;}\\ 0 \text{,}& {{\text{其他。}}} \end{array}} \right. $ | (9) |
其中:M 为连续迭代后的网格集合,g 为小区域参数,最终的优化解集表示为:
| $ \mathop \cap \limits_{i \in M} ({f_i}(\bar x) = {f_i}({\bar x^*}))\text{,} $ | (10) |
| $ F = \{ X \in {N^n}|\begin{array}{*{20}{c}} {{g_i}(X) \geqslant 0,i = 1,2,...,k;}\\ {{h_j}(X) = 0,j = 1,2,...,l } \end{array}\} \text{。} $ | (11) |
通过采用小区域进化方法得到规则的分布规律,利用拥挤方法解决问题,确保了其系统多目标优化解集非均匀性,最后得到了完美而又真实的控制情况。
3 实验结果分析为保证舰船液压起重机波浪补偿消摆控制多目标优化解集的控制稳定性,提出小区域分区进化算法进行非均匀求解。与传统方法作对比,通过设计仿真实验得出结果,实验采用传感器模拟环境。

|
图 1 船舶起重机海上风浪模拟控制区 Fig. 1 simulation control area of ship crane at sea |
利用 Visual C++6.0 软件进行编程,设置实验参数为:网格最大格数:200;进化最大次数:200;网格进化步长:len 为多目标函数的数量;重叠率:0.7;同时,引入目标函数为:
| $\begin{aligned} & {f_1}(x) = 1-\exp (-3{x_1}){\sin ^5}(4\pi {x_1})\text{;}\\ & {f_2}(x) = g({x_2})(1-{\left( {\frac{{{f_1}(x)}}{{g({x_2})}}} \right)^3})\text{。} \end{aligned}$ | (12) |
约束条件函数为:g(x2)= 1 + 10x2;同时,满足x1∈[0,1],x2∈[0,1],则此目标函数为不均匀解集。将函数实际与优化得到的解集进行比较,并采用本文方法和传统方法分别对此目标函数进行优化,用真实的解集与优化的结果进行接近程度比较,记录下比较结果,用S 表示,得到优化准确度S 的计算公式为:
| $ S = |\frac{{|F(x)-F(\bar x)|}}{{F(x)F(\bar x)-2(F(x)-F(\bar x))}}| \times 100\% \text{。} $ | (13) |
其中,
|
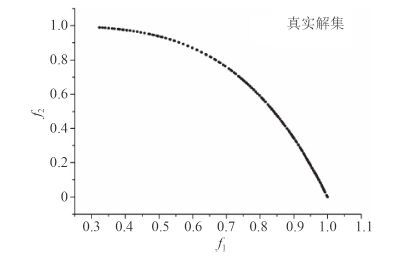
图 2 真实解集 Fig. 2 Real solution set |
|
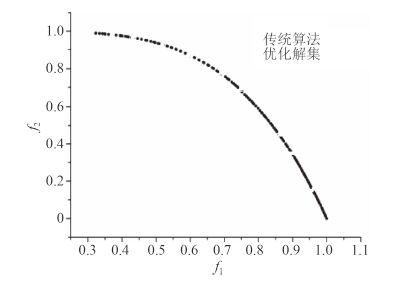
图 3 传统的控制算法的解集 Fig. 3 Solution sets of the traditional control algorithm |
|
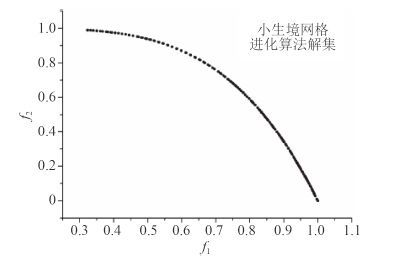
图 4 本文方法的解集 Fig. 4 Solution set of the method in this paper |
提出的算法,通过个体间的进化,保证解的不均匀性,使得得到的解集更能逼近真实解,准确度优于传统方法。
|
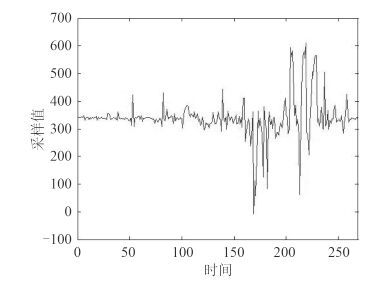
图 5 遗传算法得到控制信号 Fig. 5 Genetic algorithm to get the control signal |
|
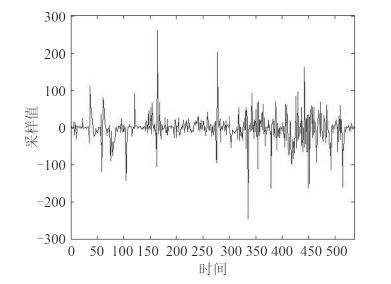
图 6 PID 算法得到的控制信号 Fig. 6 Control signal obtained by PID algorithm |
|
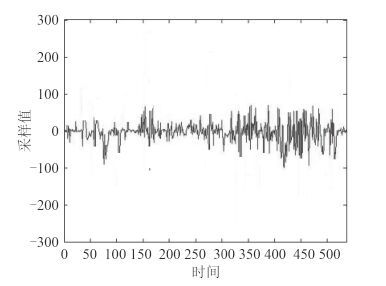
图 7 本文方法得到的控制信号 Fig. 7 Control signal obtained by this method |
为了突出本文提出方法的优点,相关实验设备是在同一船舶稳定系统环境下完成实验的。在周期性正弦命令下,翻滚角和鳍控制角形成颠簸环境模拟。比较遗传算法、PID 算法控制器本与文算法控制器的结果可以看出,对于船舶横摇稳定控制信号采集的过程中,本文方法得到的多目标优化解,在船舶颠簸状态控制命令下,通过优化小区域控制解中横摇角、鳍控制角的控制幅度。得到的数值模拟的结果最优。由于其他方法在船舶颠簸的不确定性的影响,导致机械设备稳定控制的性能发生明显退化,此外,这些控制方法在大波浪侵袭下,还存在潜在的倾覆问题。
4 结 语提出一种小区域分区进化算法,来解决舰船液压起重机波浪补偿消摆控制问题。在控制算法中引入排挤因子,利用控制数据中的相互约束作用形成小的控制单元,以此来维持控制过程的快速性,保证控制精度。实验表明,这种方法能够有效解决舰船液压起重机波浪补偿消摆控制问题,保证了船舶机械自动控制的准确性。
| [1] |
姚亮, 肖人源. 基于模型的回转式液压起重机消摆控制仿真研究[J]. 自动化应用, 2016, 23 (1):14–16.
YAO Liang, XIAO Renyuan. Rotary type hydraulic crane anti swing control model based on Simulation[J]. Automation applications, 2016, 23 (1):14–16. |
| [2] |
王孝霖, 顾含, 许历, 等. 波浪补偿起重机液压系统设计与分析[J]. 船舶标准化工程师, 2015, 30 (4):63–66.
WANG Xiao-lin, GU Han, XU Li, et al. Design and analysis of hydraulic system of wave compensation crane[J]. Ship Standardization Engineer, 2015, 30 (4):63–66. |
| [3] |
张葆华, 叶勇, 江一帆. 动力定位工程船波浪补偿控制原理的研究[J]. 船舶工程, 2015 (S1):174–177.
ZHANG Bao-hua, YE Yong, JIANG Yi-fan. The research of the technology of heave compensation in ship[J]. SHIP ENGINEERING, 2015 (S1):174–177. |
| [4] |
宣强, 朱镇. 浅淡国内首台深水波浪补偿克令吊的补偿技术系统[J]. 企业技术开发月刊, 2016, 35 (9):34–43.
XUAN Qiang, ZHU Zhen. On the first domestic deepwater wave compensation crane's compensation system[J]. Enterprise technology development monthly, 2016, 35 (9):34–43. |
| [5] |
周明健, 王幼民, ZHOUMingjian, 等. 力伺服波浪补偿吊机的液压系统研究[J]. 机床与液压, 2016, 44 (8):92–95.
ZHOU Ming-jian, WANG You-min, ZHOU Ming-jian, et al. Design of hydraulic system for force-servo wave compensation crane[J]. Machine Tool & Hydraulics, 2016, 44 (8):92–95. |
| [6] |
叶勇, 魏辽国, 江一帆. 船用波浪补偿技术的研究[J]. 船舶标准化工程师, 2015, 48 (3):6–10.
YE Yong, WEI Liao-guo, JIANG Yi-fan. Research of technology of heave compensation on ship[J]. Ship Standardization Engineer, 2015, 48 (3):6–10. |
| [7] |
艾葳, 金良安, 迟卫, 等. 舰船多层衰波媒质的振动传递矩阵模型[J]. 科学技术与工程, 2015, 15 (33):30–34.
AI Wei, JIN Liang-an, CHI wei, et al. AI vibration transfer matrix model of warship multilayered wave-attenuation media[J]. Science Technology and Engineering, 2015, 15 (33):30–34. |
| [8] |
韩新宇, 唐龙利, 简阳, 等. 舰船嵌入式软件测试用例自动驱动研究[J]. 计算机测量与控制, 2015, 23 (8):2892–2895.
HAN Xin-yu, TANG Long-li, JIAN Yang, et al. Testcase auto—drive technology for embedded software of warship[J]. Computer Measurement & Control, 2015, 23 (8):2892–2895. |
| [9] |
王梦璇. 基于小波包分解的舰船辐射噪声特征提取方法研究[J]. 电子设计工程, 2014, 22 (4):81–83.
WANG Meng-xuan. Research of ship-radiated noise feature extraction method based on wavelet packet decomposition[J]. Electronic Design Engineering, 2014, 22 (4):81–83. |
| [10] |
於建伟, 李奇. 基于关联特征提取的舰船噪声混迭谱分解[J]. 科技通报, 2015, 24 (4):154–156.
YU Jian-wei, LI Qi. Ship noise mixing spectral decomposition based on correlation feature extraction[J]. Bulletin of Science and Technology, 2015, 24 (4):154–156. |
 2017, Vol. 39
2017, Vol. 39
