为保证船舶良好的操纵性与机动性,在大型潜艇、船舶上均设置有泵阀移水系统。作为船舶辅助设备的重要组成部分,泵阀移水系统水利过渡过程中的水锤安全对于船舶的整体功能具有重要的意义和影响。在船舶泵阀移水管路系统中,由于水泵、阀门的启闭,使流速发生突然变化,从而引起对管道的压力冲击,在水体惯性和可压缩性、管壁弹性以及系统阻力作用下,管道内水的压力和密度不断交替变化,直至稳定,这一水力过渡过程状态为水锤现象[1-3]。由于船舶移水系统泵和阀门启闭频繁、流速大、管路长、水力条件复杂,系统在实际使用中存在着比较严重的水锤问题。水锤压力可达到正常运行值的数倍甚至更高,对设备和系统的稳定构成了严重的威胁。
本文针对船舶泵阀移水管路系统水锤的特点,利用 Flowmaster 软件建立系统仿真模型,分析水锤冲击的特性,并提出该系统水锤抑制的措施。
1 水锤基本理论水锤现象的起因主要是由于阀瓣位置快速变化、泵的开启和停止等。水锤的压力在扰动处的压力变化最大,其值可由 Joukowsky 方程得到:
| $ \Delta p = \rho a\Delta v\text{。} $ | (1) |
式中:∆p 为压力变化值,N/m2;ρ 为流体密度,kg/m3;a 为压力波传播速度,m/s;∆v 为流体速度变化,m/s。
船舶泵阀移水系统主要是通过关闭阀门来控制移水量。阀门关闭时,流体流动受阻,产生强烈的压力波动,在阀门处压力变化最为剧烈。压力波在管路中往复传播,且在管路摩擦的作用下逐渐减缓,此处的压力变化为最大压力变化。估算压力波传播速度可采用公式计算的方法,计算任意流体通过不同材料管道的波速。波速可由下式计算:
| $ a = \sqrt {\frac{1}{{\rho (\frac{1}{k} + \frac{{{\rm d}\varPhi }}{{tE}})}}} \text{。} $ | (2) |
式中:k 为流体体积模量,N/m2;d 为管道内径,m;t 为管道厚度,m;E 为管道材料杨氏模量,N/m2;Φ 为管道抑制因子。
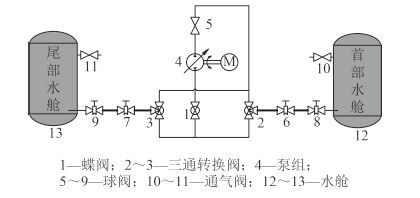
2 船舶泵阀移水管路水锤数值模拟 2.1 系统模型以某船舶泵阀移水系统为例。系统原理图如图 1 所示。泵进出口为Φ110 × 5 铜管。件号 5 为泵出口球阀,件号 6 和件号 7 为管路中间球阀,件号 8 和件号 9 为管路末端球阀,件号 12 为首部水舱,件号 13 为尾部水舱。
|
图 1 船舶泵阀移水管路系统示意图 Fig. 1 Schematic diagram of marine moving water system by pump and valves |
Flowmaster 是全球著名的流体系统仿真分析平台,以其高效的计算效率,精确的求解能力、便捷快速的建模方式被用户所采用。Flowmaster 擅长对流体管路系统进行整体分析,Flowmaster 同时是面向工程的完备流体系统仿真软件包,对于各种复杂的流体管网系统,都可以利用 Flowmaster 快速有效地建立系统模型,并进行完备的分析。
|
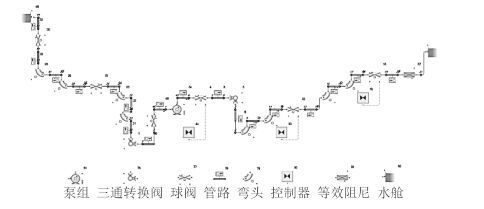
图 2 船舶泵阀移水系统模型 Fig. 2 The model of marine moving water system by pump and valves |
泵组主要参数设置如下:额定流量 50 m3/h;额定扬程 30 m;额定转速 1 450 r/min;额定功率 7.5 kW。
管路采用弹性管,主要参数设置如下:直径 100 mm;波速 1 200 m/s;绝对粗糙度 0.025 mm。
水舱采用敞口水箱,主要参数:损失系数 0.02;表面压力 0 MPa;容积 60 m3。
2.4 仿真计算运行模拟器前,输入各元件控制参量,将模拟器类型设置为“不可压缩瞬态”模式。根据弹性管道的网格尺寸,按如下公式确定仿真步长。
| $ S = L/(a\Delta t)\text{。} $ | (3) |
式中:L 为管道长度,m;a 为压力波传播速度,m/s;S 为网格数。在模拟弹性管道时,S 必须在大于 3 的整数的 ± 0.2 范围内。因此,选择时间步长 ∆t 为 0.02 s。
3 仿真结果分析系统工况动态仿真模拟船舶泵阀移水系统尾部水舱向首部水舱移水工况的全过程。仿真步长 0.02 s,仿真时间 45 s。
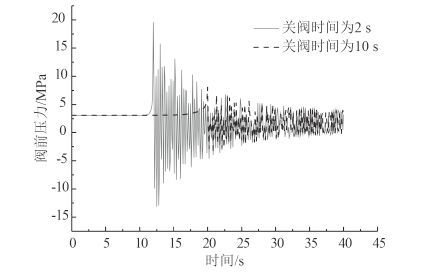
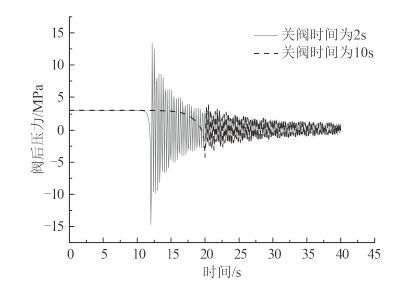
3.1 不同关阀时间的系统水锤特性仿真分析图 3 和图 4 分别为关闭泵出口阀(件号 5)前后节点的压力仿真情况。阀门在第 10 s 开始线性关闭,关闭时间分别为 2 s 和 10 s。如图 3 所示,正常工作时,泵出口阀(件号 5)阀门上游压力为 3.09 bar,当泵出口阀(件号 5)关闭时间为 2 s 时,阀门上游水锤峰值压力为 19.61 bar,当泵出口阀(件号 5)关闭时间为 10 s 时,阀门上游水锤峰值压力为 8.06 bar;如图 4 所示,正常工作时,泵出口阀(件号 5)阀门上游压力为 3.09 bar,当泵出口阀(件号 5)关闭时间为 2 s 时,阀门下游水锤峰值压力为 14.55 bar,当泵出口阀(件号 5)关闭时间为 10 s 时,阀门下游水锤峰值压力为 4.35 bar。
|
图 3 不同关阀时间阀前压力曲线 Fig. 3 Curve of pressure at upriver node of valve when the closing valve time is adjustable |
|
图 4 不同关阀时间阀后压力曲线 Fig. 4 Curve of pressure at downriver node of valve when the closing valve time is adjustable |
由不同关阀时间的系统水锤特性仿真可知:
1) 正常工作时,泵组(件号 4)工作在额定工作点;
2) 阀门突然关闭时,船舶泵阀移水系统存在明显的水锤现象,系统管路冲击压力可能会达到正常工作压力的数倍;
3) 水锤发生过程中,阀门上游节点的水锤冲击大于下游节点;
4) 延长阀门关闭的时间,能显著降低系统中水锤的冲击压力,且水锤压力波的衰减时间明显加快,是比较有效的抑制水锤的方式。
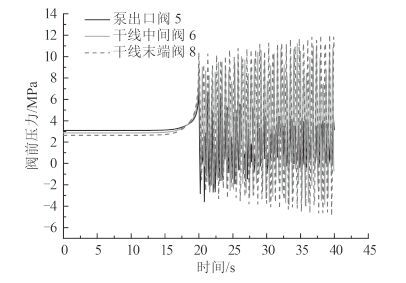
3.2 不同关阀位置的系统水锤特性仿真分析如图 1 所示船舶泵阀移水系统泵组出口系统管路有 3 个阀门,泵出口阀门(件号 5)、干线中间阀门(件号 6)和干线末端阀门(件号 8)分别进行控制。阀门在第 10 s 开始线性关闭,关闭时间均为 10 s。关闭不同位置阀门的系统水锤仿真结果如图 5 和图 6 所示。
|
图 5 不同关阀位置阀前压力曲线 Fig. 5 Curve of pressure at upriver node of valve when the place of valve is adjustable |
|
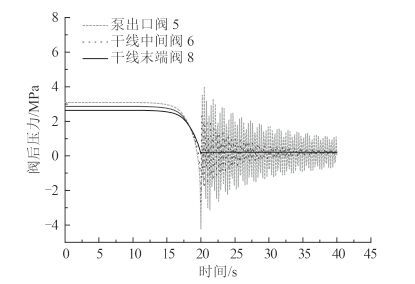
图 6 不同关阀位置阀后压力曲线 Fig. 6 Curve of pressure at downriver node of valve when the place of valve is adjustable |
如图 5 所示,当系统关闭的阀门为泵出口阀(件号 5)时,阀门上游水锤峰值压力为 8.06 bar,当系统关闭的阀门为干线中间阀门(件号 6)时,阀门上游水锤峰值压力为 11.21 bar,当系统关闭的阀门为干线末端阀门(件号 8)时,阀门上游水锤峰值压力为 12.13 bar;如图 6 所示,当系统关闭的阀门为泵出口阀(件号 5)时,阀门下游水锤峰值压力为 4.35 bar,当系统关闭的阀门为干线中间阀门(件号 6)时,阀门下游水锤峰值压力为 2.86 bar,当系统关闭的阀门为干线末端阀门(件号 8)时,阀门下游水锤峰值压力为 2.64 bar。
由不同关阀位置的系统水锤仿真可知:
1) 阀门离泵组越远,关闭阀门时系统中水锤冲击越大,由于间接水锤的作用,水锤压力波的衰减时间越长;
2) 阀门离泵组越远,对阀后水锤冲击的抑制效果越好;
3) 考虑到阀门上游节点的水锤冲击大于下游节点,因此系统水锤主要考虑阀前压力的影响。关闭系统阀门时,尽量操作系统中离泵组最近的阀是比较有效的抑制水锤的方式。
3.3 不同关阀曲线的系统水锤特性仿真分析根据上述分析可知,关闭系统阀门时,尽量操作系统中离泵组最近的阀。为进一步研究水锤抑制效果,对泵出口阀(件号 5)的关闭曲线进行优化,由线性控制改为两阶段控制,首先快关至 30°,然后慢关至全关至 0°。为与线性关闭方案对比,选取的两阶段关闭方案为 2.5 s/7.5 s。阀门在第 10 s 开始线性关闭,12.5 s 时快速关闭至 30°,20 s 时全关至 0°。不同关阀曲线的系统水锤仿真结果如图 7 和图 8 所示。

|
图 7 不同关阀曲线阀前压力曲线 Fig. 7 Curve of pressure at upriver node of valve when the closing curve is adjustable |

|
图 8 不同关阀曲线阀后压力曲线 Fig. 8 Curve of pressure at downriver node of valve when the closing curve is adjustable |
如图 7 所示,当泵出口阀(件号 5)关闭曲线为 10 s 线性关闭时,阀门上游水锤峰值压力为 8.06 bar,当泵出口阀(件号 5)关闭曲线为 10 s 两阶段关闭时,阀门上游水锤峰值压力为 5.40 bar;如图 8 所示,当泵出口阀(件号 5)关闭曲线为 10 s 线性关闭时,阀门上游水锤峰值压力为 4.35 bar,当泵出口阀(件号 5)关闭曲线为 10 s 两阶段关闭时,阀门上游水锤峰值压力为 3.09 bar。
由不同关阀曲线的系统水锤仿真可知:相同的关阀时间,相比线性关闭阀门,采用两阶段关闭阀门,阀前和阀后的水锤冲击压力都有明显减小。因此船舶泵阀移水管路系统中采用两阶段阀能有效地抑制水锤。
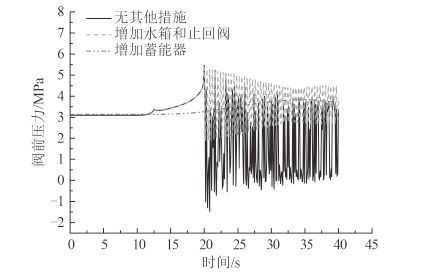
3.4 系统水锤其他抑制措施在系统管路中增加水锤抑制装置也能有效的对水锤进行抑制,考虑到船舶系统的安装空间及使用条件,采用以下 2 种措施:一是在阀前端增加水箱和止回阀[4];二是在阀前端增加蓄能器[5]。不同抑制措施的系统水锤仿真结果如图 9 和图 10 所示。
|
图 9 不同关阀曲线阀前压力曲线 Fig. 9 Curve of pressure at upriver node of valve by other methods of water hammer suppression |
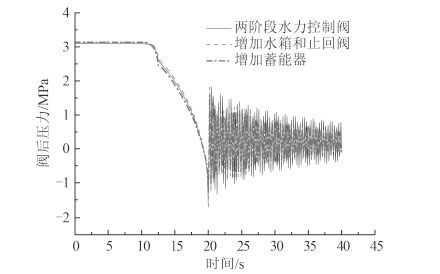
|
图 10 不同关阀曲线阀后压力曲线 Fig. 10 Curve of pressure at downriver node of valve by other methods of water hammer suppression |
如图 9 所示,当只对泵出口阀(件号 5)采用 2.5 s 30°/7.5 s 0°两阶段关闭时,阀门上游水锤峰值压力为 5.40 bar;当泵出口阀(件号 5)前增加水箱和止回阀后,阀门上游水锤峰值压力为 5.35 bar,压力峰值有一定降低,但是增加水箱和止回阀后对系统负压补偿效果非常明显,水锤压力峰谷压力为 1.87 bar,管路无负压,且水锤压力波的衰减时间明显减小;当泵出口阀(件号 5)前增加蓄能器后,阀门上游水锤峰值压力为 3.84 bar,且水锤压力波变化非常平稳。
如图 10 所示,3 条曲线在峰值和变化趋势上都比较一致。因此在阀前端增加水箱和止回阀和在阀前端增加蓄能器,对阀下游压力波动有所改善,但改善效果不明显。
4 结 语水锤问题是船舶泵阀移水管路系统中有关稳定可靠性和低噪声运行的重要问题,本文通过 Flowmaster 瞬态分析功能,建立了船舶泵阀移水系统系统,对移水系统仿真运行模拟,得到水锤压力变化曲线。计算99结果表明,在船舶泵阀移水中,阀门的关闭时间对水锤形成有较大影响,在系统流量控制精度要求范围内,尽量延长阀门的关闭时间,采取两阶段关闭的控制策略,以抑制系统水锤。另一方面,控制阀离泵组出口距离越近,抑制系统水锤效果越好。在内部空间允许的条件下,控制阀门前端采取增加水箱和止回阀、蓄能器等措施,可以有效地抑制系统水锤。
| [1] |
杨丽. 长距离大型区域压力流输水系统水锤防护计算研究[D]. 西安: 长安大学, 2009.
YANG Li. The reaserch on the protection of water hammer in large-scale regional, pressure flow and long distance water supply system[D]. Xi’an: Chang’an University, 2009. http://cn.bing.com/academic/profile?id=a1c1666eec530a7e04507c844b73bf39&encoded=0&v=paper_preview&mkt=zh-cn |
| [2] |
陈卓, 王中. 输水管路水力计算对水锤防护措施的影响[J]. 西藏大学学报, 2012, 27 (2):116–123.
CHEN Zhuo, WANG Zhong. The reaserch on hydraulic calculation of water hammer[J]. Journal of Tibet University, 2012, 27 (2):116–123. |
| [3] |
龙侠义. 输配水管线水锤数值模拟与防护措施研究[D]. 重庆:重庆大学, 2013.
LONG Xia-yi. Numerical simulation and protection measures of water hammer in transmission and distribution pipeline [D]. Chongqing: Chongqing University, 2013. |
| [4] |
刘波. 无负压加压泵站在跨海输水管线中的水锤防护性能研究[D]. 杭州:浙江大学, 2013.
LIU Bo. Study on water hammer protection performance of non-negative pressure pumping station in cross sea-water pipeline [D]. Hangzhou: Zhejiang University, 2013. http://cn.bing.com/academic/profile?id=4cd42b0ce25308663c19e6642e9c7106&encoded=0&v=paper_preview&mkt=zh-cn |
| [5] |
李良庚, 雷冬梅. 泵站水锤及防护[J]. 机电设备, 2015 (1):37–40.
LI Liang-geng, LEI Dong-mei. Prevention of water hammer in pump station[J]. Mechanical and Electrical Equipment, 2015 (1):37–40. |
 2017, Vol. 39
2017, Vol. 39
