2. 海装广州局,广东 广州 510310
2. Guangzhou Bureau of Navy Equipment Department, Guangzhou 510310, China
射流泵是一种利用高速流体带动周围流体,并起一定混合作用的设备,由于结构简单、无运动部件、密封性好、可靠性高等优点,在核工程、制冷、石油开采、清洗、材料切割等领域得到了广泛应用[1-3]。由于射流泵中冷热流体并存且压力变化较大,当局部压力低于液体当地饱和压力时,会引发空化现象。对于特定领域,如材料切割、高压清洗、岩石破碎和油井疏通等,需要利用和加强射流泵的空化气蚀现象。而在舰船系统中,射流泵中发生的空化现象会产生明显的噪声和振动、降低系统效率、造成气蚀、进而影响整个系统安全[4]。射流泵中的空化现象已经成为制约其优化设计的瓶颈,国内外研究者针对射流泵中的流场、压力场及空化规律展开了大量研究。
Pianthong 等[5]采用 CFD 方法研究了应用于喷射制冷系统中的射流泵流场,发现三维模拟结果与轴对称模拟结果相差不大,随后研究了喉嘴距、喉管长度和有效面积等因素对性能的影响,为射流泵的设计和优化提供参考。Fan 等[6]采用 CFD 对超音速射流泵内流动进行模拟,对比了不同湍流模型模拟结果,发现各种k-ε 模型的预测结果非常接近,雷诺应力模型尽管能稍微提高模拟精度,但计算量较大。随后对射流泵设计参数进行了相应优化,能显著降低真空度,并将射流泵效率从 29% 提高到 33%,能耗降低了 20%。Bartosiewicz 等[7]对比了 6 种常见的湍流模型对超音速气体射流泵的模拟精度,发现 SSTk-ω 精度最高,并发现在不同工况下 CFD 都能较准确地预测射流泵中流动情况,但同时作者提出在其他工况下,射流泵的 CFD 模拟精度如何还需进一步验证研究。梁爱国等[8]采用k-ε 模型对射流泵内部流场进行了模拟分析,得到了面积比为 3.0~8.0 时射流泵最优喉管长度的相应关联式。龙新平等[9]采用 Realizablek-ε 模型和空化模型模拟了面积比为 8.16 的射流泵内不同空化阶段的两相流动,发现数值模拟能准确预测气泡的初生、流动、破碎聚并及溃灭消逝过程,研究了不同出口压力对气蚀的影响。蔡标华[1]对射流泵内初始空化进行了实验研究,射流泵中存在空气空化和蒸汽空化 2 种空化形式,而压力降低和相对速度的增加都会引起蒸汽空化,并研究了工作压力、流量比和面积比等因素对初生空化的影响。肖龙洲等[10]采用 Realizablek-ε 湍流模型对环形射流泵内的空化流动进行模拟,指出由于速度剪切形成的漩涡中心、回流区中心位置以及喉管入口壁面处脱流等位置容易发生空化,并研究了不同吸入室角度对射流泵空化性能的影响。从上述文献综述可看出,尽管目前已经开展了大量的射流泵实验、理论和数值模拟研究,但射流泵空化研究还处于探索阶段,射流泵中压力分布情况,特别是最低压力点随不同工况下出现的规律还有待深入研究。
本文采用商业 CFD 软件 Ansys Fluent 15.0 对射流泵内单相三维流动进行数值模拟,分析射流泵内压力场,针对最容易出现空化现象的静压极小值点出现位置的变化规律进行研究,并提出了相应的优化方案,为工程设计提供参考。
1 计算模型本文首先对文献[1]中射流泵进行三维模拟以验证数值模拟的准确性,采用商业软件 Ansys Fluent 对该装置进行数值模拟。其结构和网格如图 1 所示,全部采用六面体网格,网格量约为 61 万,喷嘴直径为 12.1 mm,喉嘴距也为 12.1 mm,在喷嘴出口处有 3 mm 长圆柱过渡段,喉管直径 40 mm,喉管长度为 280 mm,扩散管长度为 225 mm,射流泵出口直径为 65 mm,射流泵面积比为 10.93。由于射流泵内流动涉及高雷诺数、强剪切等问题,所以首先需要对湍流模型进行考察选择,确定合适的湍流模型。工作流体在喷嘴出口处流速为 20 m/s,工作流体和被抽流体入口边界条件均设置为速度入口,出口设为压力出口,出口压力设为大气压。

|
图 1 射流泵结构示意图(a)及网格示意图(b) Fig. 1 The configuration and meshes of the jet pump |
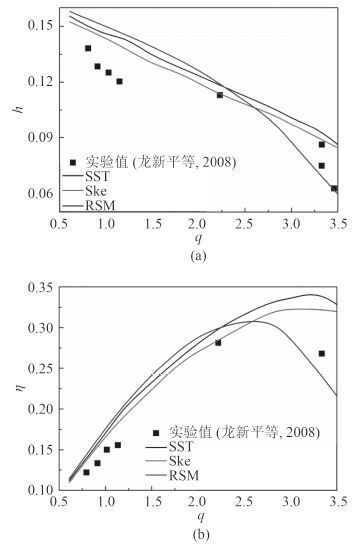
从前面文献综述可以看出射流泵内流动具有雷诺数高、剪切强等特点,要准确预测射流泵内流场就必须对湍流模型进行选择。本文对比了文献中射流泵模拟常用的雷诺应力模型(Reynolds Stress Model,RSM)、标准k-ε 模型(Ske)和 SSTk-ω(SST)模型的影响,其模拟结果如图 2 所示。其中h 为压力比,η 为射流泵效率,定义如下:
|
图 2 不同模型预测的射流泵特性曲线(a)及效率曲线(b) Fig. 2 q-h(a)andq-η(b)curves predicted by different turbulence models |
| $ \begin{array}{l} h = \displaystyle\frac{{\left( {\frac{{{p_c}}}{{\rho g}} + \displaystyle\frac{{{\nu _c}}}{{2g}} + {z_c}} \right)- \left( {\frac{{{p_s}}}{{\rho g}} + \displaystyle\frac{{{\nu _s}}}{{2g}} + {z_s}} \right)}}{{\left( {\frac{{{p_o}}}{{\rho g}} + \displaystyle\frac{{{\nu _o}}}{{2g}} + {z_o}} \right)- \left( {\frac{{{p_s}}}{{\rho g}} + \displaystyle\frac{{{\nu _s}}}{{2g}} + {z_s}} \right)}},\\[10pt] \eta = \displaystyle\frac{{qh}}{{1- h}}, \end{array} $ |
式中
从图 2 中可看出,CFD 可以较准确地预测射流泵压力比和效率随流量比的变化趋势,说明采用 CFD 研究射流泵内流动情况合理可靠。需要注意的是 CFD 预测的压力比在大部分流量比范围内都略大于实验测量值,这可能是模拟结构与实际实验结构存在偏差造成的。图 2 还显示尽管不同湍流模型预测的结果有所不同,但相差并不大,都能与实验值相符。尽管雷诺应力模型计算量比其他模型(标准k-ε 模型和 SSTk-ω 模型)偏大,但在射流泵效率预测精度方面有优势。由于雷诺应力模型并非基于各相同性湍流假设,对于射流泵这类在流场内存在强剪切的流动在本构方程方面更具优势,所以本文后续将采用雷诺时均模型对射流泵展开模拟研究。
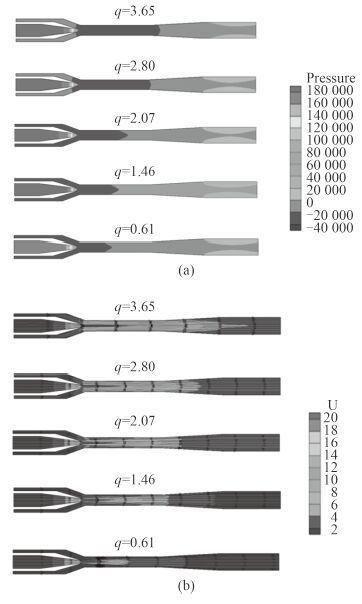
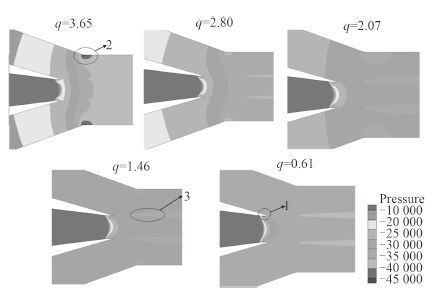
3 流场分析图 3 给出了流量比从 0.61~3.65 时射流泵内速度和压力分布云图。从图中可看出在不同流量比下,总体来说喉部区域静压较低,在这个区域中较容易产生空化气泡。喉部由于高速流体突然脱离边壁,容易造成局部的回流低压。于是进一步放大观察喉部的压力分布(见图 4),可以明显看出局部静压最低点出现在如图所示 1 和 2 区域,紧贴壁面的流体突然脱离边壁,产生局部的低压区。在流量比较低时,被抽流体速度较低,位置 2 处压力变化并不剧烈,压力最低点出现在 1 区域,随着流量比增大,被抽流体速度逐渐升高,由于流体脱离造成的回流越来越明显,位置 2 处压力越来越低,压力最低点逐渐转移到该处。在位置 3 处由于工作流体和被抽流体之间在流量比较低时存在较为明显的速度差,所以会形成较强的剪切流,此时剪切形成的漩涡也会形成一个局部低压区,但相比于 1 和 2 处,压力依然相对较高。从以上分析可以看出压力最低点,也就是最容易发生空化的位置一般出现在位置 1 和 2 处,要避免在该位置发生空化,继 而抑制气蚀和噪声,主要需对这两位置结构进行优化。
|
图 3 不同流量比时射流泵内压力(a)及速度(b)分布云图 Fig. 3 The velocity and pressure contours at various flow ratios |
|
图 4 喉管局部压力分布云图 Fig. 4 Local pressure distributions at the throat region |
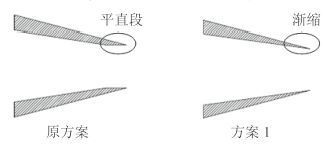
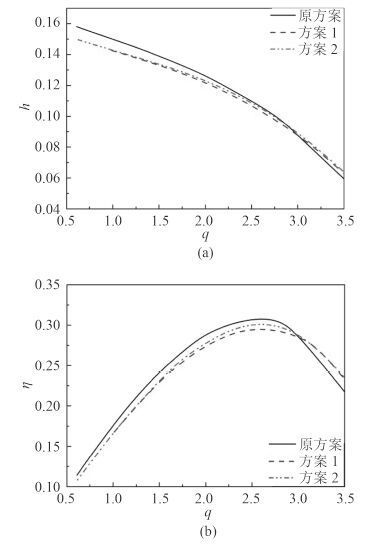
针对位置 1 和 2 处压力较低,容易发生空化的问题,本节对这两处结构进行优化。从上面分析可以看出静压过低主要是由流体脱离壁面造成的,所以首先我们对位置 1 处进行结构优化,新方案中喷嘴采用渐缩结构而不采用平直段(如图 5 方案 1 所示)。图 6 给出了修改后的射流泵特性曲线及效率曲线,可以看出 2 种方案在特性曲线和效率方面相差不大。在低流量比时,原方案效率稍高,在高流量比时,方案 1 效率较高,但总的来说相差并不大,由此可见将喷嘴出 口平直过渡段改为渐缩结构并不会显著影响射流泵效率。
|
图 5 方案 1 喷嘴修改示意图 Fig. 5 Optimization adopted in plan 1 |
|
图 6 优化方案与原方案特性曲线(a)及效率曲线(b)对比 Fig. 6 Comparison of theq-h(a)andq-η(b)curves between the original and optimization plans |
图 7 给出了方案 1 与原方案射流泵最低静压随流量比的变化关系,从图中可以看出在较低流量比时,采用方案 1 渐缩喷嘴结构,射流泵中的最低静压相比于原方案明显升高,能有效抑制该处的空化。在高流量比时 2 种方案最低静压相差不大,甚至原方案最低静压要相对高一点。结合图 4 和图 9 可看出,采用渐缩喷嘴结构,在喷嘴出口处不会存在由流体脱离壁面而形成的低压区,所以在低流量比时最小静压值要明显升高。而在高流量比时,最低静压点出现在喉部连接处(图 4 中的位置 2),所以改变喷嘴结构并不能改善喉管衔接处的最低静压。

|
图 7 优化方案与原方案最低静压对比 Fig. 7 Comparison of the minimum static pressure between the original and optimization plans |
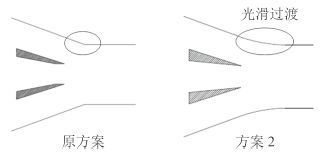
为避免被抽流体突然脱离壁面,可在图 4 所示 2 处位置采用光滑曲面过度,方案 2 即在方案 1 的基础上对在喉部位置外壁面进行光顺化处理,示意图如图 8 所示。图 6 给出了方案 2 的射流泵特性曲线及效率曲线,可以看出方案 2 射流泵的特性曲线和效率曲线与方案 1 十分接近,同时也与原方案类似。也就是说对喉管部进行光滑过渡处理并不会对泵特性和效率产生明显影响。
|
图 8 方案 2 结构示意图 Fig. 8 Optimization adopted in plan 2 |
图 7 同时给出了方案 2 中静压最低值随流量比的变化情况,可以看出方案 2 在本文模拟的所有流量比中均比原始方案静压最低值高,即方案 2 结构能有效减小或抑制空化现象的发生。在低流量比时,静压最低值与方案 1 接近。原始方案中静压最低点位置随着流量比的增加逐渐从喷嘴出口处(位置 1)转移到喉管边壁(位置 2),由于方案 2 对喉管边壁进行了光顺化处理,能有效抑制流体突然脱离壁面引起的边界层分离现象,从而不容易形成局部低压区,进一步抑制空化现象的发生。
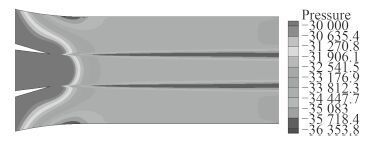
查看方案 2 喉部压力分布(见图 9),可以看出方案 2 中低压区集中在喉部(图 4 中位置 2)以及工作流体与被引流体接触发生强剪切处(图 4 中位置 3),所以要进一步升高最低静压,需要对图 4 中位置 2 处喉部结构进行进一步优化,或者如文献所述,采用两级射流泵以抑制空化现象发生[11]。
|
图 9 方案 2 局部压力分布云图 Fig. 9 The local pressure contour for the plan 2 |
本文对射流泵内三维流动情况进行了单相流数值模拟,重点考察了射流泵内静压最低点出现位置,主要结论如下:
1)不同湍流模型均能较为准确预测射流泵的特性曲线和效率曲线,相对来说雷诺应力模型与实验结果更接近;
2)随着流量比增大,静压最低点位置由喷嘴出口平直过渡段逐渐转移到喉部衔接处;
3)喷嘴出口取消平直段,采用渐缩结构及对喉部衔接处进行光顺化处理能在不影响射流泵效率的前提下显著提高最低静压值,抑制空化。
| [1] | 蔡标华. 射流泵初生空化及其试验研究[D]. 武汉: 武汉大学, 2005. |
| [2] |
乌骏, 袁丹青, 王冠军, 等. 射流泵的发展现状与展望[J]. 排灌机械 , 2007, 25 (2):65–68.
WU Jun, YUAN Dan-qing, WANG Guan-jun, et al. Current situation and prospect of jet pumps[J]. Current situation and prospect of jet pumps , 2007, 25 (2) :65–68. |
| [3] | WINOTO S H, LI H, SHAH D A. Efficiency of jet pumps[J]. Journal of Hydroulic Engineering , 1997, 126 (2) :150–156. |
| [4] |
龙新平, 何培杰. 射流泵气蚀问题研究综述[J]. 水泵技术 , 2003, 4 :33–38.
LONG Xin-ping, HE Pei-jie. A review on the investigation of cavitation phenomenon within jet pumps[J]. A review on the investigation of cavitation phenomenon within jet pumps , 2003, 4 :33–38. |
| [5] | PIANTHONG K, W. S., BEHNIA M, SRIVEERAKUL T, APHORNRATANA S. Investigation and improvement of ejector refrigeration system using computational fluid dynamics technique[J]. Energy Conversion & Management, 2007, 48: 2556-2564. |
| [6] | FAN J, J. E. THOMPSON H M, TOROPOVE V V, KAPUR N, COPLEY D, MINCHER A. Computational fluid dynamic analysis and design optimization of jet pumps[J]. Computers & Fluids , 2011, 46 :212–217. |
| [7] | BARTOSIEWICZ Y, Z. A., ZDESEVAUX P, YVES MERCADIER. Numerical and experimental investigations on supersonic ejectors[J]. International journal of heat and fluid flow , 2005, 26 :56–70. DOI: 10.1016/j.ijheatfluidflow.2004.07.003 |
| [8] |
梁爱国, 刘景植, 龙新平, 等. 射流泵内流动的数值模拟及喉管优化[J]. 水泵技术 , 2003, 1 :3–6.
LIANG Ai-guo, LIU Jing-zhi, LONG Xin-ping, et al. Numerical simulation of the flow inside the jet pump and optimization of the throat[J]. Numerical simulation of the flow inside the jet pump and optimization of the throat , 2003, 1 :3–6. |
| [9] |
龙新平, 程茜, 韩宁, 等. 射流泵空化流动的数值模拟[J]. 排灌机械工程学报 , 2010, 28 (1):7–11.
LONG Xin-ping, CHENG Qian, HAN Ning, et al. Numerical simulation on cavitating flow within jet pump[J]. Journal of Drainage and Irrigation Machinery Engineering , 2010, 28 (1) :7–11. |
| [10] |
肖龙洲, 龙新平. 吸入室角度对环形射流泵空化性能的影响[J]. 浙江大学学报(工学版) , 2015, 49 (1):123–129.
XIAO Long-zhou, LONG Xin-ping. Influence of inclined angle on cavitation performance of annular jet pump[J]. Journal of Zhejiang University (Engineering Science) , 2015, 49 (1) :123–129. |
| [11] |
顾磊, 张景松, 杨春敏. 气蚀工况液体射流泵的实验研究[J]. 流体机械 , 2006, 34 :7–9.
GU Lei, ZHANG Jing-song, YANG Chun-min. Experiment on the liquid jet pump in cavitation[J]. Fluid Machinery , 2006, 34 :7–9. |
 2017, Vol. 39
2017, Vol. 39
