2. 中船重工集团公司 渤船集团,辽宁 葫芦岛 125000
2. Bohai Ship Campany of CSIC, Huludao 125000, China
随着我国经济发展,能源安全以及海洋战略的发展提出更高需求。在陆上核电复苏和规模建设的同时,船用核动力装置技术也在不断前进,其可以适用于船舶动力、岛屿供电、海水淡化、海洋资源开发等。海上浮动核电站、核动力商船等动力装置的发展越来越受到各国的重视,包括国际原子能机构、英国、俄罗斯在内发达国家都开展了海上浮动平台的研制。而我国多家核能开发单位,包括中广核、中核、中船重工等都正在全力推进海上浮动平台的研发与建设。
核动力系统是核动力船舶的心脏和主动脉,其承担了核动力船舶的动力以及正常电力的供应,该系统的运行安全可靠影响到核动力船舶或浮动平台远洋工作、项目完成甚至船舶与船员的生存,是核动力船舶安全的重心。与陆上核电站的运行状态不同,船用核动力系统既要满足船舶动力、供电等负荷变化的需求,还需要适应海洋环境的带来腐蚀、摇摆的影响,另外还要考虑空间要求、运行性能、可靠性和可维护性等多项性能指标,所以核动力系统的设计与运行有着显著的特点。
1)复杂的运行环境与有限的布置空间
由于船用核动力装置内部空间有限,所以在动力系统设备布置以及系统设计方面,只可能考虑系统必备的系统配置,很多辅助的安全措施都是复用,甚至一些监督手段都未曾采用。与核电站相比,我国现运行的核动力装置虽然配备有独立的专设安全措施,但是最终冷源依旧需要外部动力提供。而另一方面,船用核动力装置受海洋环境的影响,由于倾斜,摇摆会对大量的重要信号带来较大的误差,而这些信号往往都会导致触发系统的安全预警或保护。
2) 核动力系统冗余配置与运行组合多变
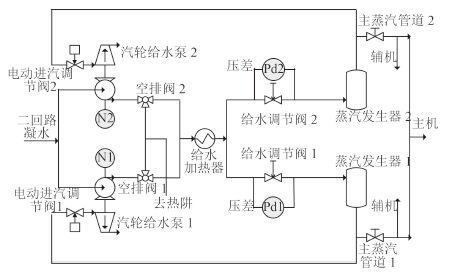
鉴于核动力系统运行的特殊要求,一方面要保证装置的安全运行,另一方面又受到设计空间的约束,所以在系统设计时,往往都是提高各个动力设备的运行负载能力,同时,采用左右两舷设备互为备用的设计思路。以图 1 的动力装置给水系统为例。
|
图 1 核动力装置给水系统 Fig. 1 Feedwater system of NPP |
图 1 为核动力装置的给水系统原理图,其中 2 个汽轮给水泵都同时具备 100% 给两舷供水的能力,所以在实际运行中,2 台泵并车运行,如果有 1 台泵发生故障,可以依靠另 1 台泵实现两舷供水。与此相比,大亚湾核电站,每个汽轮机组配有 2 台汽轮给水泵, 1 台电动给水泵备用,各有满足 50% 的负荷的供水能力,实际运行时,2 台汽轮给水泵运行,当发生故障时,投入备用的电动给水泵。由于系统冗余配置的设计方案,而且动力装置运行工况多变,各种工况运行设备的组合也不尽相同,在高低运行工况下,投 入运行的设备数量大不相同,系统运行的特征也不一样。
3)核动力系统负荷多变,瞬态响应要求高
由于装置任务与工作的不同,与核电站长期额定功率运行不同,核动力装置运行负荷多变,而且其瞬态响应要求高,其动态运行条件与核电站具备 10% 阶越或者 5%/min 的线性功率变化要求的苛刻程度有天壤之别。快速的瞬态变化会导致动态参数变化剧烈,极可能导致越限报警,触发误保护动作信号。如蒸汽发生器水位,在大幅度升功率或者降功率过程中,由于蒸汽压力的波动,易产生“假水位”信号。
4)核动力系统信息构成的复杂性
鉴于上文所描述的核动力装置运行环境、工况、系统配置的差异,最终必然导致核动力系统信息构成的复杂性与多元化。核动力系统运行中相关的信息类型可以分成以下几种:
① 运行环境相关的信息:船舶的运行姿态(摇摆、倾斜、速度),海水压力,温度;
② 运行设备的配置状态:投入运行设备的状态,如泵的高低速,投入与切除信号;
③ 长期运行的特征参数:设备老化、管路腐蚀、金属疲劳、滑油磨粒;
④ 定值运行的过程参数:如稳压器压力、水位,蒸汽发生器水位,冷凝器水位等信号;
⑤ 随负荷变化的过程参数:蒸汽流量、给水流量、泵转速、阀位开度等
所以,对于核动力系统的运行评估必须与船舶实际运行的状态紧密相连,考虑单工作状态的诊断与评估都无法真正适用于装置的运行。
2 核动力装置配置、运行特点引出的几大难题上文详细论述了核动力装置设计、配置、运行的特点,这些特点对动力装置系统设计与运行安全性的评估带来了一下几大难题。
1)冗余系统配置带来的风险隐藏
复杂系统的故障可能相互独立, 也可能相关, 即故障间存在相依性。单纯的可靠性分析中若仅考虑独立故障, 将低估系统故障概率。核动力装置由于存在大量冗余设计, 因部件的独立随机故障而引起系统失效的概率很小, 但受到相关故障的影响, 系统在使用中的实际可靠性就低得多。现运行装备曾发生过,由于保护系统采用的三取二的设计原则,保护输出的一路输出板卡长期故障而没有发现,直到另一路供电电源发生故障触发应急停堆事故才被发现。冗余系统配置系统可以提高系统运行的安全性,但是如何评估系统运行的安全性是当前装置设计的一大难题。以上文 2 台泵 100% 备用给水为例,亦可以设计为 4 台各 50% 的配置方案,但是孰优孰劣,需要有一套科学的评价体系。
2)运行中状态参数的不确定性
由于核动力装置运行环境复杂,工况多变且测点信息有限,所以在现在的系统设计中,基本都是采用的定阈值报警,而系统的 FMEA 也仅仅是定性分析,对于运行中故障现象没有量化的指标与方法,无法将测点的信息与故障描述内容结合起来,如水位过高的原因是调节阀卡阀,但是如果量化卡阀这个指标以及其发生概率,这个是现在系统运行评估中缺乏的重要一环。
3)动态过程的运行评估技术
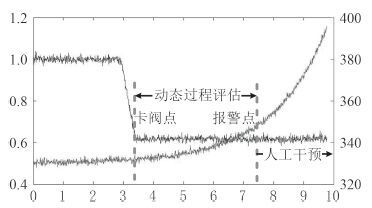
核动力装置负荷变化过程多,动态过程响应快,所以由此带来了动态过程特性相对较差,控制难度大的问题。而系统设计时,是以单阈值限值对运行过程的故障实施报警。如图 2 所示,在大负荷降功率过程时,如果发生给水调节阀发卡阀,则极易导致蒸汽发生器满水,使二回路辅助系统压力上升烫伤人员。从发生卡阀到满水过程历时近 3 min,而等到水位信号达到报警值之前,有近 2 min的时间没有被关注,应该提出一种适合于分析此类动态过程状态迁移的评估技术。
|
图 2 水位与阀位动作示意图 Fig. 2 Operation characters of water level affected with the valve |
综上,当前核动力系统运行评估的主要核心是需要针对系统的复杂性和信息的不确定性开发技术层面上切实有效的评估技术。而作为量化处理不确定信息以及信息间传递相关性的强大工具,概率图模型(probabilistic graphical models)一直是不确定推理和智能计算的重点研究领域。对概率图模型的研究不仅包括模型结构和依赖关系的表述,还包括利用这些模型进行的推断和产生信度的过程。上文论述中已经清楚论述了核动力系统的 3 个数学特征:不确定性;复杂的系统结构;存在时变的状态转移。而针对核动力系统设计、稳态运行以及动态过程中运行状态评估的问题,都可以采用贝叶斯网络或者连续时间贝叶斯网络的数学结构进行表述,并基于网络节点间的概率分布对装置运行可信度进行分析计算,以此寻找系统设计的薄弱环节,评估运行状态,分析运行风险,为操作员人为干预提供足够的操作时间。
3 国内外研究现状及分析对于从事与核相关设计的工作,核安全是一个永恒的话题,而核动力系统作为海洋中的孤岛电站,其保障条件比不上核电站,而保证核动力正常运行的要求却比核电站运行苛刻。所以,需要加强其运行不确定性问题的评估研究。
国际上现已成熟的核动力系统故障分析都是人们在运行核电厂的实践中逐步积累发展起来的, 通过半个多世纪的发展, 国际上建立了一套完整而详尽的安全分析体系。这套系统被国际社会认可, 并在国际原子能机构的监督下实施。核电厂核动力系统的运行故障分析及对策研究是进行核动力系统安全分析的重要组成部分, 核动力系统故障分析经历了 2 个阶段, 70 年代中期以前确定论安全分析方法为基础进行研究, 它是以纵深防御概念[1] 为基础, 以确保反应性控制、堆芯冷却和放射性包容 3 项基本安全功能为目标, 针对一套确定的设计基准工况, 采用一套保守的假设和分析方法, 确保任何故障下堆芯的安全。1975 年美国原子能委员会基于概率风险评价(PRA)的 WASH1400“反应堆安全研究”报告发表, 这项运用故障树(FTA)方法[2] 和事件树(ETA)方法的研究报告的结果在 1979 年三里岛核事故中得到验证, 概率安全评价由此得到了广泛的认可, 以 PRA 为基础运用 FTA 法和 ETA 法进行故障分析也得到广泛运用。现在的核安全设计准则以及概率风险评估[3] 都是以假设基准事故前提下对核安全发生概率的分析,对于核动力系统,除了核安全还有对应的装置安全,而且对实际运行状态的评估要以数据驱动分析,而不是假设基准事故,这个是当前问题与 PRA 之间本质的区别。
在国内,陈玲等[4]首先提出了船用核动力系统技术状态综合评估模型研究,并针对部分失效情况下的动力装置技术状态实施评估[5], 张永发等[6]提出了核动力装置的安全目标。刘永阔等[7-8]结合神经网络对核动力装置故障实施诊断,而谢春丽等提出了信息融合的方法[9]。在国际上,KunMo 等[10]提出了动态神经网络模型对核动力装置瞬态实施故障诊断的方法,Jinkyun 等[11]较早提出了核动力装置诊断系统框架的概念,而 Tae-Ho Woo 等[12]提出了基于层次分析法(AHP)的核动力装置运行安全评估研究。近几年来,基于多层流方法的核动力系统故障诊断受到越来越多的重视,杨明等[13]将多层流的方法与核动力装置相结合,提出了基于多层流的核动力装置故障诊断的方法,而詹静采用了基于多层流模型对核动力装置的可靠性进行了研究[14]。纵观当前核动力系统评估的技术发展,大量的研究还仅仅出于理论研究,没有结合核动力装置运行的实际状态以及系统组成出发,层次分析法需要大量人为定义的中间层次,而多层流方法只能考虑按照能量流,物质流的方向进行建模,其他的智能算法如神经网络不能显式表征系统信息间的逻辑关系。另外,当前的诊断方法都无法评估动态过程的运行特征。
基于对核动力系统运行不确定性的现状,本文提出了结合贝叶斯网络的核动力系统运行不确定性评估的方法。贝叶斯网络的搭建是基于运行故障的因果关系,它既能显式表现系统的关系,还可以考虑系统配置,运行方式的不同,其比单一的多层流建模方法更为科学。另外,对于网络拓扑结构的优化与推理有一套完善的计算方法,可以有效对复杂系统建模进行优化计算。此外,基于贝叶斯网络可以对系统动态过程实施量化评估,这是其他方法所无法胜任的。
自从 1986 年 Pearl 提出概率图网络[15-16] 的概念后,贝叶斯网络目前己应用于很多领域,如美国国家科学研究会研制的核电站状态评估系统,美国通用电气公司的 Auxiliary Turbine Diagnosis 工业故障诊断系统;美国航空航天局和 Rockwell 公司联合研制的航天故障诊断系统等;微软的主打产品 Windows2000 和 Office 系列等很多产品在很多方面融入了贝叶斯网络等[17]。
而结合概率图网络对工程应用中不确定性问题的诊断与评估已经成为了一个研究热点。Jun Su-ha 提出了基于层次分析法与贝叶斯网络结合的安全特征分类的方法[18], 文献[19-20]以空间站为背景提出了搭建用于诊断的贝叶网络。而 Hussian 采用贝叶斯网络对过程控制故障诊断的不确定性进行了研究[21]。Xie S 采用贝叶斯网络对卫星动力系统进行了故障诊断[22]。贝叶斯网络除了对它应用的研究,还有大量的对网络计算,学习方法的研究,如文献[23-26]。对于网络拓扑结构以及复杂系统的概率计算对解决实际的工程问题有着很好的帮助作用。
4 基于贝叶斯网络的状态评估研究方案及可行性分析 4.1 核动力系统静态设计状态的失效评估方案由于核动力装置动力系统的结构复杂,在对系统进行状态评估时,必须先确定系统故障传播的架构,根据核动力系统的配置以及设计目标设计系统设计状态下的贝叶斯网络,然后分析各个边缘节点的失效概率,实现对系统静态设计失效评估。
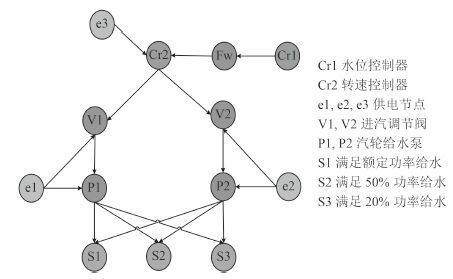
以图 1 所示的给水系统为例,按照系统的运行控制方式设计单舷上水的贝叶斯网络,如图 3 所示。
|
图 3 给水系统静态设计状态贝叶斯网络结构 Fig. 3 Bayesian network of the feedwater system static state |
图 3 为给水系统设计状态下基于故障传播的贝叶斯网络结构,从图 3 可见,当 e3 供电节点出现故障,对给水系统带来的影响比单台泵故障带来的风险要大,而现在采用以物质流、能量流的多层流建模方式对动力系统的故障诊断有一定缺陷,装置的故障发生原因是多方面的,在实际运行中就曾发生过由于控制电源丧失,导致控制器误动作,最终阀门全开,蒸汽泄漏的事故。所以,对于静态以故障传播方式建立的贝叶斯网络,主要研究由于供电、控制、或者冗余设计带来的系统运行失效概率,而设计阶段的网络架构先验概率都是非此即彼的两值分布,静态设计的评估主要是计算边缘节点的失效概率,由此指导工程的维修与更换。对于运行过程的评估是结合 FMEA 或者 FTA 实施的。
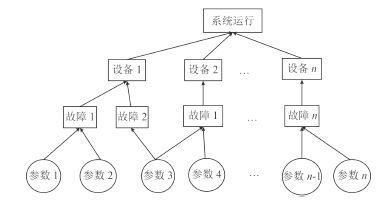
4.2 结合 FMEA 的核动力系统运行状态评估方法当前面对的第 2 类问题就是评估核动力系统在长期运行中,由于设备疲劳、老化、管道腐蚀而带来的系统运行风险,其仅仅考虑外部电气设备或者弱电控制设备的故障概率(相比工艺系统,电子电气设备更容易出现问题)带来的系统风险,而在实际的运行中,泵、阀的状态评估必须以泵阀实际运行的状态信息进行量化评价,而系统的运行评估是结合 FMEA 搭建的贝叶斯网络。运行状态评估是核动力系统评估最核心的内容,对实际装置的运行与诊断有着很好的辅助作用。其具体技术线路如图 4 所示。
|
图 4 系统运行时评估结构图 Fig. 4 Evaluation structure diagram during system operation |
在装置的实际运行中,任何评估计算的落脚点都是系统运行中的各个参数,所以,对系统运行状态的评估关键之处有 3 点,一是系统的结构,这个是由系统设计或者运行规范确定的,二是各种故障的量化分析,即是用于计算贝叶斯网络的边缘概率,三是各种故障对上层设备的条件概率。如给水泵的冷却水丧失会带来给水泵定子温度升高,但是不一定会导致给水泵功能丧失。先验概率是贝叶斯网络计算推理的基础,也是难点之一。
4.3 基于 DBN 模型的动态过程运行评估核动力装置复杂系统的评估技术分三大部分,静态网络,稳态运行网络以及动态时间网络。由于核动力装置负荷变化大,现在尚没有任何对于负荷变化过程评估诊断方法的应用。所以针对此问题,可以利 用动态贝叶斯网络(DBNs)对系统动态过程进行评估。
DBNs 是以概率论和影响图为基础,把传统的静态贝叶斯网络模型和随时间变化的隐马尔可夫模型相结合的动态模型。既去除了静态贝叶斯不能随时间变化的缺陷,又去除了隐马尔可夫模型只能通过观察序列推测已有状态、不能添加新状态的缺陷,同时又保持了 2 个模型的优点。
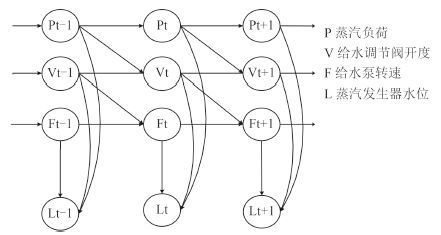
以上文描述的给水系统动态过程为例,图 5 为给水过程的网络时序图,该模型首先是以蒸汽负荷、给水调节阀开度、给水泵转速作为导致水位信号变化的事件组,同时在时序上有基于蒸汽负荷-给水调节,给水压力-汽轮机转速两组事件,系统状态 转移的过程为蒸汽负荷-给水调节阀-给水泵转速-水位。
|
图 5 给水过程动态贝叶斯网络时序图 Fig. 5 Bayesian network sequence diagram of feedwater system dynamic process |
在实际应用中,可以根据连续运行的数据计算网络节点间的条件概率如P =P(Vt|Pt-1),以此作为全网络计算的基础,当发生蒸汽负荷下降而给水调节阀阀位卡阀时,给水调节阀评估的失效概率上升,由此计算最终导致水位上升的概率加大。
上述仅仅是通过给水过程为例简单描述了 DBNs 网络对核动力装置复杂系统的评估方法,但是 DBNs 的构造以及计算有一套完整的理论与计算方法,各个节点边缘概率分布以及节点间的条件概率分布都需要经过计算验证,对核动力系统状态评估的最后一项研究目标就是将 DBNs 理论与核动力装置运行紧密连接,用以评估核动力装置运行状态,对运行中可能发生的故障进行提前预警,给操作员有足够的操作时间进行干预,毕竟现在采用的阈值越线报警都是后验型方法,当发生报警时,系统的故障已经发生。
5 结语如上文所述,从信息交互角度,可将核动力装置的健康管理功能分成 7 个层次,分别为传感器层、信号处理层、状态监控层、诊断层、健康评估层、决策支持层以及人机交互层,当前核动力系统的设计中,缺乏的就是最难以量化的评估层,以及由此影响的决策支持层的研究。
本文所提出的不确定条件下核动力系统运行状态评估是一个全新的领域,它已经超越了单纯的故障诊断的内容,本文提出结合贝叶斯网络评估装置运行不确定性问题的解决方案,提出了解决核动力系统评估三大问题的方案:静态设计状态的评估、稳态运行状态的评估以及动态过程的状态评估。采用贝叶斯网络结构,其原因是它是处理复杂系统不确定性问题的有效手段,同时又能显式表征系统各节点间的逻辑关系,其处理方法与结果更具有说服力。在后续的研究中,将会结合具体对象对核动力系统的三大问题进行进一步的研究。
| [1] | 虞镇国. 核电站安全性的探讨[J]. 能源工程 , 1990 :21. |
| [2] | 王乃彦. 核电站安全性分析[J]. 院士论坛 , 2008, 24 (6):14. |
| [3] | 陈济东. 大亚湾核电站PSA主报告[R]. 深圳: 广东核电集团, 2001. |
| [4] | 陈玲, 蔡琦, 蔡章生. 船用核动力系统技术状态综合评估模型研究[J]. 船海工程[J] , 2006, 35 (2):22–24. |
| [5] | 陈玲, 蔡琦, 蔡章生. 基于部分失效的潜艇核动力系统技术状态评估[J]. 系统工程理论与实践 , 2006, 26 (9):141–144. |
| [6] | 张永发, 童节娟, 蔡琪, 周羽. 船舶核动力装置安全目标的初步研宄[J]. 核科学与工程 , 2011, 31 (1):55–56. |
| [7] | 刘永阔. 核动力装置故障诊断智能技术的研究. 哈尔滨工程大学博士学位论文[D], 2006. |
| [8] | 刘永阔, 夏虹, 谢春丽. 智能故障诊断技术在核动力装置中的应用研究. 哈尔滨工程大学学报[J]. 2007, 28(2), 241-246. |
| [9] | XIE Chun-li, XIA Hong, LIU Yong-kuo. Data Fusion Method Application to Fault Diagnosis of Nuclear Power Plant[J]. Journal of marine science andapplcation , 2005, l (4) :30–33. |
| [10] | KUN MO, SEUNGJUN LEE, POONG HYUNSEONG. A dynamic neural network aggregation model for transient diagnosis in nuclear Power Plants[J]. Progress in Nuclear Energy , 2007, 30 (3) :1–11. |
| [11] | JINKYUN PARK, WONDEA JUNG. A study on the systematic framework to develop effective diagnosis procedures of nuclear Power Plants[J]. Reliability Engineering and System Safety , 2004, 84 :319–335. DOI: 10.1016/j.ress.2003.12.004 |
| [12] | TAE-HO WOO, UN-CHUL LEE. Safeguard assessment in nuclear power plant operartions using analytic hierarchy process(AHP)and production function[J]. Multi Science Publishing , 2011, 29 (3) :337–356. |
| [13] | YANG. M. Application of a semiotic analysis method based on multilevel flow models for real-time diagnosis system of PWR plant[C]//. 2004 Annual Meeting of the Atomic Nuclear Society of Japan, 2004: 368. |
| [14] | 詹静. 基于多层流模型的可靠性分析方法在核动力装置中的应用[D]. 哈尔滨: 哈尔滨工程大学. 2007. |
| [15] | PEARL J. Fusion, propagation and structuring in belief Networks[J]. Artificial Intelligence , 1986, 29 :241–288. DOI: 10.1016/0004-3702(86)90072-X |
| [16] | JENSEN F V. Propagation in DAGs. Introduciton to Bayesian networks[M]. London: UCL press, Manuscript in Progress, 2001. |
| [17] | 张晓丹. 汽车发动机故障诊断中不确定性问题的贝叶斯网络解法[D]. 吉利: 东北大学, 2005. |
| [18] | JUN SU HA, POONG YYUN SEONG. A method for risk-informed safety significance categorization using the analytic hierarchy process and Bayesian belief networks[J]. Reliability Engineering and System Safety , 2004, 83 :1–15. DOI: 10.1016/j.ress.2003.08.002 |
| [19] | M. ROEMER, E. NWADIOGHU, G. BLOOR. Development of diagnostic and prognostic technologies for aerospace health management applications[C]//. In IEEE Aerospace Conference Proceedings, 2001, 6: 193-202. |
| [20] | PRZYTULA K W, THOMPSON D. Construction of Bayesian networks for diagnostics[C]//. Aerospace Conference Proceedings. IEEE, 2000, 5: 193-200. |
| [21] | HUSSAIN S, HOSSEIN A, GABBAR H A. Tuning of fault semantic network using Bayesian theory for probabilistic fault diagnosis in process industry[C]//. International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering (QR2MSE), 2013: 1677-1682. |
| [22] | XIE S, PENG X, ZHONG X, et al. Fault diagnosis of the satellite power system based on the Bayesian network[C]//. Computer Science & Education (ICCSE), 8th International Conference on. IEEE, 2013: 1004-1008. |
| [23] | SCUTARI M, BROGINI A. Bayesian network structure learning with permutation tests[J]. Communications in Statistics-Theory and Methods , 2012, 41 (16-17) :3233–3243. DOI: 10.1080/03610926.2011.593284 |
| [24] | HECKERMAN D, GEIGER D, CHICKERING D M. Learning Bayesian networks: The combination of knowledge and statistical data[J]. Machine Learning , 1995, 20 (3) :197–243. |
| [25] | PENA J M, LOZANO J A, LARRANAGA P. An improved Bayesian structural EM algorithm for learning Bayesian networks for clustering[J]. Pattern Recognition Letters , 2000, 21 (8) :779–786. DOI: 10.1016/S0167-8655(00)00038-6 |
| [26] | KJRASULFF U B, MADSEN A L. Bayesian Networks and Influence Diagrams: A Guide to Construction and Analysis: A Guide to Construction and Analysis[M]. Springer, 2012. |
| [27] | 石东昱. 适合分布计算环境不确定性处理的概率图模型若干问题研究[D]. 上海: 上海大学, 2006. |
| [28] | MILONE D H, GALLI J R, CANGIANO C A, et al. Automatic recognition of ingressive sounds of cattle based on hidden Markov models[J]. Computers and Electronics in Agriculture , 2012, 87 :51–55. DOI: 10.1016/j.compag.2012.05.004 |
| [29] | ALKHATEEB J H, PAUPLIN 0, REN J, et al. Performance of hidden Markov model and dynamic Bayesian network classifiers on handwritten Arabic word recognition[J]. Knowledge-Based Systems , 2011, 24 (5) :680–688. DOI: 10.1016/j.knosys.2011.02.008 |
| [30] | DOIJ E, CHEN C, PECHT M. A Bayesian Hidden Markov Model-based approach for anomaly detection in electronic systems[C]//. In: Proceedings of the 34th IEEE Aerospace Conference, Big Sky MT, USA: 2013, 1-10. |
| [31] | TORABIAN ESFAHANI M, VAHIDI B. A new stochastic model of electric arc furnace based on hidden Markov model: A study of its effects on the power system[J]. IEEE Transactions on Power Delivery , 2012, 27 (4) :1893–1901. DOI: 10.1109/TPWRD.2012.2206408 |
| [32] | GEORGOULAS G, MUSTAFA M O, TSOUMAS I P, et al. Principal Component Analysis of the start-up transient and Hidden Markov Modeling for broken rotor bar fault diagnosis in asynchronous machines[J]. Expert Systems with Applications , 2013, 40 (17) :7024–7033. DOI: 10.1016/j.eswa.2013.06.006 |
 2017, Vol. 39
2017, Vol. 39
