在风浪流环境力作用下,为了保证海洋平台的安全作业,需要装备适当的定位系统来保证其运动在允许的安全范围内。一般来说,常用的定位方式主要有锚泊定位、动力定位和锚泊辅助动力定位等,其中,锚泊定位发展时间较早,是一种较为传统的定位方式,通常用于浅水中海洋平台的定位[1 -3]。
在锚泊系统设计中,海洋平台的安全性是第一位的,所设计的锚泊定位系统首先要满足平台的定位需求,保证其安全作业;其次,要考虑锚泊系统本身的安全性,如锚链的破断强度要足够大,足以承受工作海域给定海况下的可能出现的最大张力,保证不出现锚链断裂的情况[4]。
常规锚泊系统的锚链多沿着平台的各个方向对称布置,分散固定在海底锚点处,从而整个系统可以为平台提供回复力和力矩,用以抵抗各种作用在平台上的环境力,控制平台的位置和首向变化[5]。本文研究的平台其工作地点位于南海岛礁附近,特点是水深极浅,地势复杂,锚泊的布置方式和受力情况也变得非常复杂。受限于岛礁附件有限的空间,以及工作需要靠近岛礁的需求,在经济、安全的前提下,本文使用非对称方式布置锚链[6 -8]。为增加锚链与海底摩擦力,提高平台在偏离平衡位置后的回复力,在锚链上起始段布置了许多重块[9]。
针对该复杂岛礁环境所设计的非对称锚链定位精度和安全问题是本文分析的重要问题。极浅水中系泊系统所采用的锚链上配置有许多重块,其对锚泊系统安全问题的影响也是值得研究与分析的要点。
1 平台运动响应理论 1.1 坐标系随船坐标系oxyz固定在平台上,随平台摇荡,平台处于平衡位置,oxy 平面与静水面重合,oz 轴垂直向上,与平台中心轴重合。
大地坐标系OXYZ,当平台在平衡位置时候,与随船坐标系重合,但其不随平台摇荡,始终处于平衡位置。
1.2 平台时域运动方程在随船坐标系中,平台时域运动方程[10]为:
| $ \begin{array}{l} \left( {M + m} \right){\ddot x}\left( t \right) + \int_{ - \infty }^t {{K}\left( {t - \tau } \right)} {{\dot x}}\left( t \right){\rm{d}}\tau + C{x}\left( t \right) = \\ {F^{F - K}} + {\rm{ }}{F^D} + {\rm{ }}{F^w} + {\rm{ }}{F^C} + {\rm{ }}{F^{sn}}\left( t \right) + {\rm{ }}{F^m}\left( t \right)。 \end{array} $ | (1) |
式中:
将FF-K 和FD 合称为一阶波浪力Fw ,Fw 可根据 Cummins[11]提出的时域与频域波浪力的卷积关系计算:
| $ \left\{ {\begin{array}{*{20}{l}} {{F_{wi}}\left( t \right) = \int_0^t {h_i^1\left( {t - \tau } \right)} {\rm{d}}\tau },\\ {h_i^1\left( t \right) = \frac{1}{\pi }\int_0^\infty {H_i^1\left( \omega \right){e^{i\omega t}}{\rm{d}}\omega } }。 \end{array}} \right. $ | (2) |
式中
二阶波浪力Fsn 采用 Newman 近似计算,根据间接时域法,即采用频域格林函数法计算浮体的附加质量、阻尼和波浪作用力,通过快速傅里叶变换,将频域水动力系数变为时域水动力系数[12]。
通过傅里叶变换,求得延迟函数:
| $ {K_{ij}}\left( t \right) = \frac{2}{\pi }\int_0^\infty {{ \lambda _{ij}}} \left( \omega \right)\cos \left( {\omega t} \right){\rm{d}}\omega, $ | (3) |
式中 λ 为频域中浮体的阻尼阵。
时域中浮体附加质量为:
| $ {m_{ij}} = {\mu _{ij}}({\omega _0}) + \frac{1}{{{\omega _0}}}\int_0^\infty {{K_{ij}}(t)\sin ({\omega _0}t){\rm{d}}t}。 $ | (4) |
式中:μ 为频域中浮体附加质量阵;ω0 为任意值。
风力和流力计算根据 OCIMF 提供的资料进行计算,风力计算经验公式为:
| $ {F^w} = 0.611v_k^2{c_h}{c_s}A, $ | (5) |
流力计算公式为:
| $ {F^c} = 0.5\rho {C_D}{u^2}A $ | (6) |
式中:vk 为风速;ch 为风压高度系数;cs 为形状系数;A 为迎风面积;CD 为流力系数;u 为流速;A 为迎流面积。
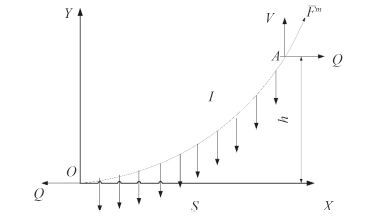
锚链系泊力Fm 可采用悬链线方程计算,锚链视为完全挠性,不能传递弯矩,如图 1 所示。图 1中,A 为上部平台导出点,OA 为锚索悬垂部分,O 端与海底相切处,l 为曲线OA 长度,S 为OA 水平投影,h 为水深,w 为锚索单位长度的重量。OA 线上各点都受到拉力,但A 点的拉力Fm 最大。Q 为海底锚的水平拉力。V 为Fm 的垂直分力,它与锚索重平衡。
|
图 1 锚索的悬垂线 Fig. 1 Catenary of anchor cable |
极浅水中,锚索长度不足 400 m,可以使用单一成分的锚索,因此只考虑全锚链形式。悬链线方程为:
| $\begin{aligned} \frac{{l - s}}{h} = \mathop {\left( {2q + 1} \right)}\nolimits^{\frac{1}{2}} - q\mathop {\cosh }\nolimits^{ - 1} \left( {\frac{{q + 1}}{q}} \right) =\\ \quad\mathop {\left( {2t - 1} \right)}\nolimits^{\frac{1}{2}} - \left( {t - 1} \right)\mathop {\cosh }\nolimits^{ - 1} \left( {\frac{t}{{t - 1}}} \right)。 \end{aligned}$ | (7) |
式中:
半潜平台水动力计算采用势流软件计算,锚泊系统设计与分析采用 SESAM 和 Orcaflex 软件,风力、流力的估计值采用水池模型实验的结果。
2.1 平台附加质量和阻尼系数半潜平台主要参数如表 1 所示。
|
|
表 1 半潜平台主要参数 Tab.1 Main parameter of semi-submersible platform |
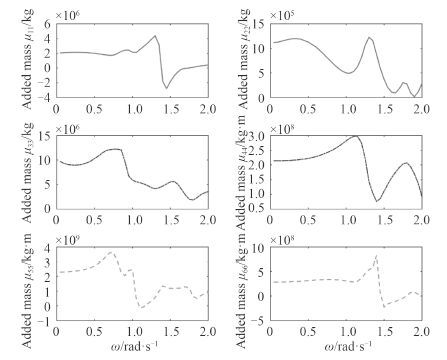
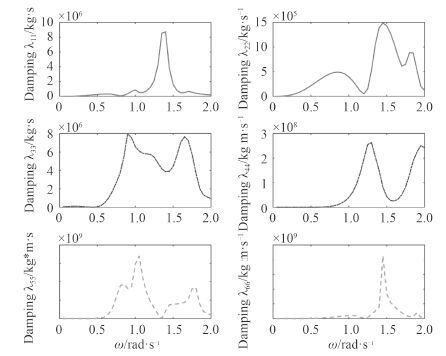
图 2 和图 3 为平台附加质量系数和势流阻尼系数。由图 2 和图 3 可知,对于水平面三自由度运动模态,附加质量系数在 1.4 rad/s 附近,出现峰值,过了该峰值后,随波浪频率的升高而急剧减小;在 1.4~1.5 rad/s 之间的波频区,出现势流阻尼的最大峰值。
|
图 2 附加质量系数 Fig. 2 Added mass coefficient |
|
图 3 势流阻尼系数 Fig. 3 Damping coefficient |
而对于垂直面三自由度运动模态,在 0.6~1.2 rad/s 区间,附加质量出现最大峰值,过了峰值点后,其值随着波浪频率的升高而减小。附加质量在波频响应下较大,阻尼在较高频的波浪响应下较大。根据三维势流理论,附加质量和阻尼系数增大会导致平台所受水压力增大,对其运动响应会产生较大的影响。
2.2 设计工况和环境载荷表 2 列出了平台在海上工作的海洋环境条件。由于平台位于南海岛礁,深水波浪传递至平台位置时,波浪方向逐渐垂直于海岸线[13],因此本文主要考虑平台在 90 ℃首向进行作业。模拟波浪谱采用北海联合海浪计划(JONSWAP)谱。
|
|
表 2 环境工况参数 Tab.2 Environment parameters |
悬链式锚链具有良好的对海底的抗磨损性,对锚的抓力有较好的作用,因此在极浅水时可以使用全锚链系统,而不必使用合成索和钢丝绳[14]。
锚链采用铸铁锚链,铸铁环直径为 66 mm,每节铸铁锚链长度为 27.5 m,重约 2 766 kg,最大破断力3 300 kN。根据 API RP 2SK 规范[15],对于完好的系泊系统,使用准静态分析计算时,锚链最大张力的安全因子取 2.0;使用动力分析时,锚链安全因子取 1.67[16]。
浅水锚泊系统锚链拖底段较长,平台飘曳范围增大[17],因此为了增大稳性,设计在每根锚链靠近导缆孔一侧加部分配重块。距导缆孔 10 m处开始布配重块,相邻配重块间距 5 m,每个配重块重 5 t,每根锚链固定 10 个配重,配重同时具有增加锚链与海底之间摩擦力的作用。
在锚泊定位系统中,通过调整锚链预张力的大小,可以调整结构物的定位精度。本文选取的预张力为 23 t。
2.4 极浅水锚泊系统布置与深水作业的半潜平台相比,浅水布置锚泊较为简单。而且因为半潜平台正向和侧向面积差别不大,作用在各个方向上的环境力相当,可以采用辐射状布置锚链。
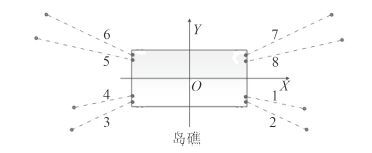
考虑岛礁附近海底地形特点,以及半潜平台靠近岛礁的工作特点,靠岛屿一侧缺少足够的空间布置锚链,因此靠岸侧锚链相应缩短长度。所以本次的锚泊系统采用的是 8 点分散式悬链线系统,且靠岸一侧锚链长度较短[18],如图 4 所示。每点连接 1 根锚链,共 8 根。
|
图 4 锚链分布 Fig. 4 Mooring chain distribution |
1)工作海况
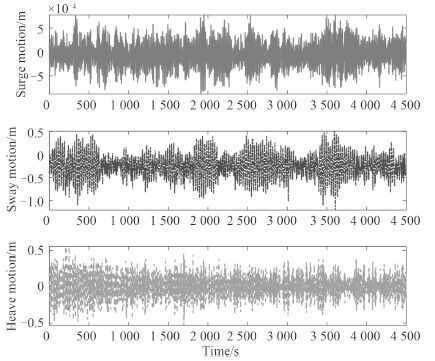
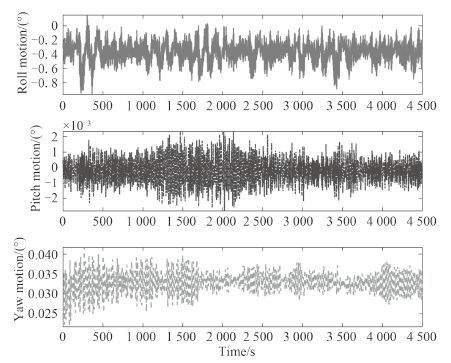
工作海况下,平台的纵荡、横荡、垂荡运动时历如图 6 所示,横摇、纵摇、首摇运动时历如图 7 所示。表 3 列出了平台在工况海况下六自由度运动的统计结果。
|
图 5 工作海况纵荡,横荡,垂荡运动时历 Fig. 5 Operation condition surge, sway, heave time history |
|
图 6 工作海况横摇,纵摇,首摇运动时历 Fig. 6 Operation condition roll, pitch, yaw time history |
|
|
表 3 工作海况六自由度运动统计结果 Tab.3 Operation condition 6-DOF statistical result |
由图 5 和图 6 的结果可知,在所给环境力条件下,平台能较好地进行定位,最大横荡偏移位置为 1.2 m,最大横摇角度为 0.96° 左右。平台垂荡数值也较小,最大垂荡位移为 0.55 m,不会发生触底风险。
该种锚链布置方式能提供相对很大的首摇恢复力矩,在这种较小的环境力作用下,平台不会产生很大首摇角。
平台最大横荡位移为 1.2 m,最大横摇角度 0.96°,其标准差分别为 0.26 m,0.14°。因此在给定的环境条件下,该平台的定位性能优秀。较小的标准差也反映了该锚泊系统的稳定性。
2)生存海况
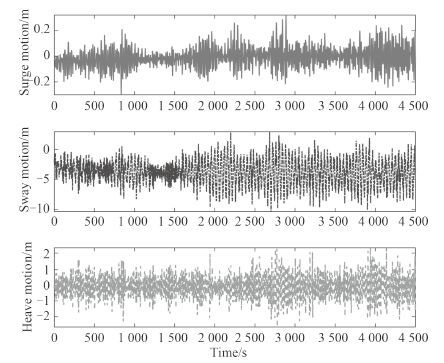
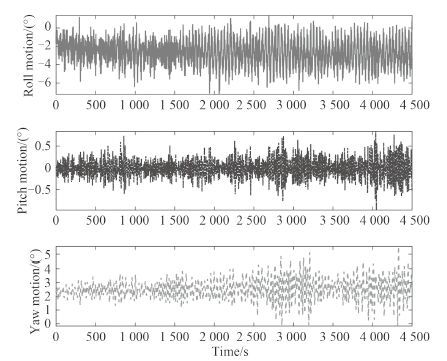
生存海况下平台的六自由度运动统计值如表 4 所示,纵荡、横荡、垂荡运动时历如图 8 所示,横摇、纵摇、首摇运动时历如图 9 所示。
|
|
表 4 生存海况六自由度运动统计结果 Tab.4 Survival condition 6-DOF statistical result |
|
图 7 生存海况纵荡,横荡,垂荡运动时历 Fig. 7 Survival condition surge, sway, heave time history |
|
图 8 生存海况横摇,纵摇,首摇运动时历 Fig. 8 Survival condition roll, pitch, yaw time history |
从六自由度运动时历运动图可以发现,该平台横漂较大。这是由于该平台采用的八根锚链定位,在生存海况下为了锚链安全,预张力相对较小;而且,生存海况风速达到了 36 m/s,平台受到很大的风力。因此,在上述综合作用下,平台产生较大的横漂。
平台的首摇运动较大,原因是平台上层建筑的不对称,导致平台受到的风力实际上在首摇方向上有一个力矩。
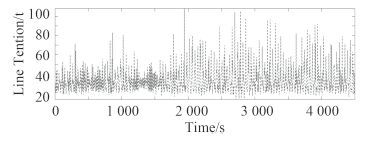
3.2 导缆孔处锚链张力时历分析锚链较大的张力发生在生存工况中。图 9~图 10 和表 5 分别给出了生存海况下受力最大的2根锚链张力时历与统计结果。
|
图 9 生存海况6号锚链张力 Fig. 9 Force of line 6 in survival condition |
|
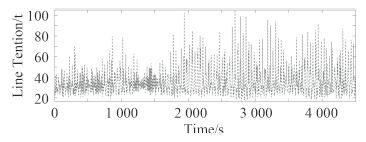
图 10 生存海况7号锚链张力 Fig. 10 Force of line 7 in survival condition |
|
|
表 5 生存海况 1~8 号锚链张力 Tab.5 Survival condition line 1~8 force |
生存海况中锚链受到的最大张力为 108 t,小于锚链破断强度 330 t,安全系数为 3.05,远大于设计安全系数 1.67,不会有锚链破断的情况出现,其中 6 号和 7 号锚链受力标准差较大,说明张力值变化频率与幅值较大,需要注意防止其疲劳断裂。
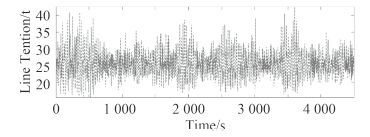
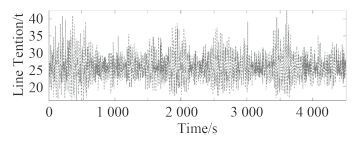
图 11~图 12 和表 6 为工作海况下受力最大的2根锚链张力和统计结果。相对于生存海况,工作海况下锚链拉力较小,最大值为 43 t,远远小于破断张力,不会有锚链破断的情况出现,其中 6 号和 7 号锚链受力标准差相对生存海况也较小,疲劳断裂的风险较低。
|
图 11 工作海况6号锚链张力 Fig. 11 Operation condition line 6 force |
|
图 12 工作海况7号锚链张力 Fig. 12 Operation condition line 7 force |
|
|
表 6 工作海况 1~8 号锚链张力 Tab.6 Operation condition line 1-6 force |
由于锚链上间隔布置了配重,因此锚点受到的抓力并不大。
表 7 给出了生存工况下锚点抓力统计结果,这也是锚点抓力最大的工况。
|
|
表 7 1~8 号锚点处抓力 Tab.7 Line 1-8 anchor force |
可以发现,锚点抓力分为明显不同的 2 组,即迎风浪一侧 4 根和背风浪一侧 4 根这 2 组。迎风浪一侧的 5~8 号锚点受到较大的拉力,所以锚点抓力较大。其中最大的力为 90 t,属于比较小的量级,这跟锚链特点有关,拖底段较长,以及锚链上间隔布置的 5 t 重块,都阻碍了锚链导缆孔处的拉力传递到锚点处,因此不会发生走锚的危险[19]。
4 结语对极浅水下平台的锚泊定位进行了系泊系统设计和时域模拟分析。在工作海况下,平台整体运动响应较小,定位精度较高,不会发生触底现象,且系泊系统各部分受力均满足相关要求。在生存海况下,平台整体运动响应虽然较大,但满足平台生存海况下运动允许的范围,锚泊系统满足生存海况下的破断要求。根据不同工况下的时域模拟结果,可以证明该套锚链用于极浅水下平台的定位是安全可行的。
本文较好地解决了近岛礁浅水环境下浮式平台的系泊问题,可为平台的水池模型试验和极浅水下平台系泊系统的设计提供参考。
对于岛礁周围复杂海域的开发,由于复杂地形问题,经常会遇到类似的不规则锚泊设计问题。其可以在保证结构物定位精度的前提下,减少经济成本,对此进行研究有很大的工程意义。
极浅水中锚泊定位,系统优化空间受到限制,可以在锚链上配重增加锚链与海底的摩擦力,提高平台定位稳定性,减少起锚的风险。
| [1] |
吴德烽, 杨国豪. 船舶动力定位关键技术研究综述[J]. 舰船科学技术 , 2014, 36 (7):1–6.
WU De-feng, YANG Guo-hao. Review on key techniques for ship dynamic positioning system[J]. Ship Science and Technology , 2014, 36 (7) :1–6. |
| [2] |
王世圣, 等. 3 000米深水半潜式钻井平台运动性能研究[J]. 中国海上油气 , 2007, 19 (4):277–280, 284.
WANG Shi-sheng, et al. Review on key techniques for ship dynamic positioning system[J]. Study on motion performance of 3000 metersdeep-water semi-submersible drilling platform , 2007, 19 (4) :277–280, 284. |
| [3] |
刘海霞. 深海半潜式钻井平台的重量控制探述[J]. 中国海洋平台 , 2011 (06).
LIU Hai-xia. Weight Control of Deepwater Semi-submersible Drilling Unit[J]. Weight control of deepwater semi-submersible drilling unit , 2011 (06) . |
| [4] |
张峰, 王磊, 李勇跃. 锚泊辅助动力定位系统单缆失效影响研究[J]. 海洋工程 , 2012 (03):P29–34.
ZHANG Feng, WANG Lei, LI Yong-yue. Research on the impact of one line failure for a mooring assisted dynamic positioning system[J]. Research on the impact of one line failure for a mooring assisted dynamic positioning system , 2012 (03) :P29–34. |
| [5] | JOHANNING L, SMITH G. H, WOLFRAM J. Measurements of static and dynamic mooring line damping and their importance for floating WEC devices[J]. Ocean Engineering , 2007, 34 (14-15) :1918–1934. DOI: 10.1016/j.oceaneng.2007.04.002 |
| [6] | 李璐. Truss Spar和半潜式平台的水动力及运动性能对比研究 [D]. 大连: 大连理工大学, 2010. |
| [7] | |
| [8] |
苏一华, 杨建民, 肖龙飞. 深海单柱式平台及其系泊系统的截断水深模型试验[J]. 上海交通大学学报 , 2007, 41 (9):1454–1459.
SU Yi-hua, YANG Jian-min, XIAO Long-fei. The Experiment of a Deepwater Spar and Its Mooring System at Truncated Water Depth[J]. Journal of Shanghai Jiaotong University , 2007, 41 (9) :1454–1459. |
| [9] | 亓俊良, 龚玉林, 杨贵强. 系泊锚链配重链替代配重块工程实践[C]//. 2012年度海洋工程学术会议2012: 厦门. |
| [10] | 刘应中, 缪国平. 船舶在波浪中的运动理论[M]. 上海: 交通大学出版社, 1987. |
| [11] | CUMMINS W E. The impulse response function and ship motions[J]. Schiffstechnic , 1962 (9) :101–109. |
| [12] | 童波, 杨建民, 李欣. 深水半潜平台悬链线式系泊系统藕合动力分析[J]. 中国海洋平台. |
| [13] |
吴宋仁.
海岸动力学[M]. 北京: 人民交通出版社, 2004.
Wu Songren. Coastal Hydrodynamics[M]. Beijing: China Communications Press, 2004. |
| [14] | 潘斌. 移动式平台设计[M]. 上海: 上海交通大学出版社. 1995. |
| [15] | 浮式结构定位系统的设计与分析规范[S]. |
| [16] | 童波. 半潜式平台系泊系统型式及其动力特性研究[D]. 上海:上海交通大学,2009. |
| [17] | Nuno Fonseca Ricardo Pascoal, T. M. R. D., Design of a mooring system with synthetic ropes for the FLOW wave energy converter. 2009. |
| [18] |
马鉴恩, 李凤来. 锚泊列阵的设计与研究[J]. 海洋工程 , 1996 (1):56–62.
MA Jian-en Li Feng-lai. The Design and Research On Multipoint Mooring System[J]. The design and research on multipoint mooring system , 1996 (1) :56–62. |
| [19] | 唐尧. 船舶走锚运动方式的研究[D]. 大连: 大连海事大学, 2012. |
 2017, Vol. 39
2017, Vol. 39
