2. 核动力舰船蒸汽动力系统国防科技实验室,湖北 武汉 430064
2. National Lab of Science and Technology on Steam Power for NS, Wuhan 430064, China
船舶碰撞是船舶与其他物体之间发生接触造成结构破坏损伤事故的一种现象。主要包括与静止物体发生碰撞,如桥梁、礁石、码头、岸边、海洋工程类结构、停泊或抛锚的船舶;与运动物体发生碰撞,如漂浮的冰山、航行的船舶、运动的海洋结构物等。船舶碰撞往往具有惯性大、速度较低等特点。船舶碰撞是一种严重的事故,往往会引起很严重的后果,如船舶毁坏或沉没、人员伤亡、环境污染、被撞结构物损坏等。
目前,船舶碰撞相关的研究可以根据其研究方法分为 2 类:一类是基于一定的理论基础和实践经验,在试验数据的基础上,推导计算碰撞破坏宏观量的经验公式[1-2]。经验公式计算比较简便,通过初步的计算便可以对船舶碰撞特性进行大致的分析,适用于工程上的初步设计阶段;另一类是通过一系列小尺度缩比试验,结合有限元仿真计算,研究不同结构形式下船体的耐撞性能[3-4],这是现在主流的研究方法。但由于碰撞试验多为破坏试验,试验代价较高。随着计算机技术的快速发展,有限元仿真分析方法逐渐成为船舶碰撞破坏问题的主要研究手段。
对于碰撞过程中结构的破坏,选择合适的失效准则是保证数值仿真准确性的关键因素。近年来,学者在进行仿真计算时,多假定当等效塑性应变达到某一临界值时该结构发生断裂。该临界值多通过静态单轴拉伸试验来获得。为了考虑实际情况下结构的受力状态,一些学者通过特定的板壳结构准静态破坏试验来测量极限塑性应变。McDermott[5]通过纵向加筋壳板的静压试验,建议取 0.1 作为被撞船外壳板的断裂应变值。Su zuki 等[6]在讨论舷侧结构的碰撞强度时,取临界失效应变为 0.25。Paik[7]通过研究指出结构中每个构件的临界断裂应变值可能是不相同的,并在双壳油轮结构防碰撞设计中假定取 0.1 作为其平均值。
在碰撞过程中材料多处于动态加载状态,用单一的失效应变来判定材料破坏的准确性还没有得到有效验证。目前工程上对于金属材料的延性失效破坏,尚没有形成统一的准则。比较常用的极限塑性失效准则(GL)[8]、RTCL(Rice-Tracey and Cockcroft-Latham)失效准则[9]、PES 失效准则[10]和 JC(Johnson-Cook)失效准则等[11]。
本文以典型船体双层壳结构碰撞破坏为研究对象,结合已有文献试验数据,在尖刀型撞头低速碰撞下,对比仿真和试验的双层壳结构的塑性变形,对有限元模型设置、本构模型和网格尺寸等因素进行对比验证。分别采用 GL,RTCL 和 JC 失效准则,对双层壳结构在圆锥形撞头下的破坏进行仿真,对比分析不同准则的适用性,旨在为后续相关研究提供一定的参考。
1 模型验证碰撞冲击破坏中存在很多非线性因素,如结构的大变形、材料的非线性力学特性、接触的非线性等。在进行船舶碰撞研究时,这些因素将直接影响分析结果的准确性。因此,为保证后续分析有效性,本节结合文献[12]中所提供试验数据对有限元模型及参数设置进行验证。
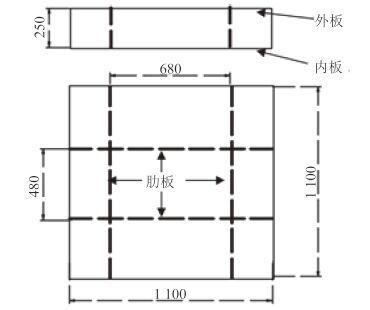
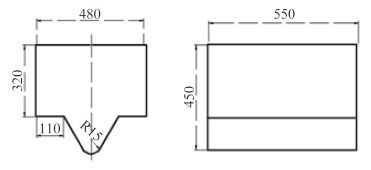
1.1 几何模型双层壳结构内外板之间连接板的形式有很多种,其中比较典型为矩形板。由于船体板架结构尺寸一般较大,在进行仿真研究时,过大的模型会使得网格量很大,不便于进行一些细观因素的讨论。因此本文选择典型小尺度的双壳矩形板架结构为研究对象,其结构尺寸如图 1 所示,外板尺寸为 1 100 mm × 1 100 mm × 2.6 mm,内板尺寸为 1 100 mm × 1 100 mm × 2.4 mm,肋板尺寸为 1 100 mm × 250 mm × 3.2 mm。模型在 ABAQUS/Explicit 模块中建立,采用三维壳单元建模。撞头的形状为尖刀形,如图 2 所示。撞头定义为解析刚体,在保证计算精度的情况下能够节省一定的计算资源,撞头初速度为 6.22 m/s,质量为 400 kg。计算时,对双层壳底板两侧边线全约束,对撞头约束除垂向平动外所有自由度。
|
图 1 双层壳结构尺寸 Fig. 1 Structure size of the double shell |
|
图 2 尖刀型撞头尺寸 Fig. 2 Size of the knife edge indenter |
撞头和双层壳的外板、肋板和内板之间均定义接触,接触类型为 Automatic Surface to Surface。为避免撞头与外板的初始厚度产生接触干涉,撞头的初始位置位于中心,略高于双层壳结构。
1.2 材料参数船体结构多采用低碳钢材料,如 Q235,Q345 等。在弹性阶段,杨氏模量为 206 GPa,泊松比为 0.3,密度为 7 850 kg/m3。在塑性阶段,采用 JC 本构描述其材料力学特性,其表达式为:
| $ \sigma = (A + B{\varepsilon ^n})(1 + C\ln {\dot \varepsilon ^ * })(1- {T^ * }^m)。 $ | (1) |
式中:ε 为等效塑性应变;
|
|
表 1 JC 本构模型参数 Tab.1 Parameters of JC constitutive model |
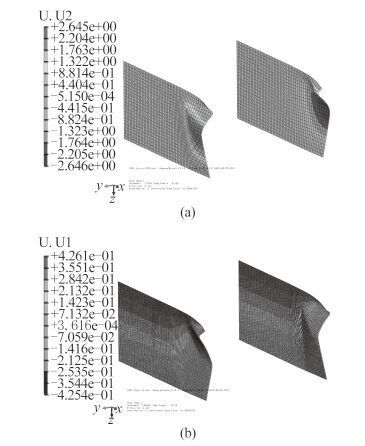
分别对双层壳结构进行 3 种不同的网格划分,最小网格尺寸分别为 10 mm,5 mm 和 3 mm。将仿真计算结果与试验结果进行比较,验证有限元模型设置、本构模型参数的准确性。从图 3和图 4 可看到,双层壳结构的外板变形情况,外板中心部位受到撞击发生了较大的塑性变形,往两边塑性位移逐渐减小,在肋板位置处,塑性变形被阻止,横向肋板是为第二大吸能结构。图 5 为仿真中横向肋板的变形形式,可以看到,在承受垂向冲击的情况下,横向加筋受压,其结构的变形可以分为即向冲击中心偏移和远离中心方向偏移 2 种。对比图 3~图 5 仿真结果与文献[12]中试验结构变形形式发现,两者十分吻合。

|
图 3 双层壳结构变形图 Fig. 3 Deformation of the double shell |

|
图 4 外板撞击变形图 Fig. 4 Deformation of the outer plate |
|
图 5 仿真横向肋板变形图 Fig. 5 Deformation of stringers on simulation |
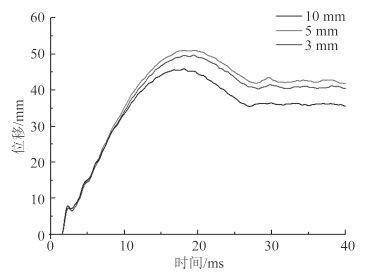
图 6 为 3 种不同网格尺寸下,撞击中心点的位移曲线。可以看到,变形位移在撞头速度为 0 时达到最大,随后结构吸收的弹性能释放,给予撞头反向速度的能量,外板中心的位移有所下降,随着撞头的脱离,最终达到稳定。由表 2 中仿真计算值与试验测量值的对比可知,仿真值与试验值十分吻合。
|
图 6 撞击中心垂向位移曲线 Fig. 6 Vertical displacement curves in impact center |
|
|
表 2 仿真与试验外板最大位移值对比 Tab.2 Comparison of the maximum displacement of the outer plate between simulation and experiment |
1)GL 失效准则。采用单一的等效临界失效应变预测损伤起始,但与常应变准则不同的是临界值的确定方法不一致,GL 根据材料沿厚度方向的应变值来判断单元是否失效。
沿厚度方向的临界失效应变值的经验公式为:
| $ {\varepsilon _f}({l_e}) = {\varepsilon _g} + {\varepsilon _e} \cdot \frac{t}{{{l_e}}}。 $ | (2) |
式中:εg 为平均应变;εe 为局部塑性颈缩应变;t 为板厚;le 为单个单元的长度。参考文献[8]给出了平均应变εg 和颈缩应变εe 的值分别为 0.056 和 0.54。
2)RTCL 准则。以细观损伤力学为基础,通过研究材料内部球形孔洞的生长规律,给出 Rice-Tracey 韧性失效准则失效判据表达式为:
| $ \begin{array}{l} D = \int_0^{{{\bar \varepsilon }_f}} {\frac{{{\sigma _1}}}{{{\sigma _m}}}{\rm d}\bar \varepsilon } {\rm{- 0}}{\rm{.33}} < \eta < 0.33,\\[3pt] D = \int_0^{{{\bar \varepsilon }_f}} {\frac{1}{C}\exp (1.5\eta ){\rm d}\bar \varepsilon } {\rm{ }}\eta > 0.33。 \end{array} $ | (3) |
式中:
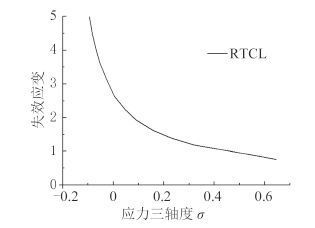
临界断裂应变随应力三轴度的变化曲线如图 7所示。
|
图 7 RTCL 失效准则失效应变与应力三轴度曲线 Fig. 7 Strain-stress triaxiality curves of RTCL failure criteria |
3)JC 失效准则。综合考虑应变硬化、应变率效应及温度软化效应,其具体形式为:
| $ {\varepsilon _f} = ({D_1} + {D_2}\exp {D_3}{\sigma ^ * })(1 + {D_4}\ln {\dot \varepsilon ^ * })(1 + {D_5}{T^ * })。 $ | (4) |
式中D1,D2,D3,D4,D5 为材料参数,参考文献[13],其取值如表 3 所示。其他物理量参照 JC 本构方程。
|
|
表 3 JC 失效模型参数 Tab.3 The parameters of JC failure criteria |
在对模型准确性进行验证时,双层壳结构模型只发生了较大的塑性变形,并没有破裂。为了研究不同失效准则的适用性,需要改变条件,使结构发生破坏。在保证双层壳结构形式不变的情况下,有增大撞头的撞击速度和改变撞头的形状 2 种途径。若增大撞头的撞击速度,材料的应变率效应增加,材料本构数据将会有一定的偏差,影响结构耐撞性,不便于进行失效准则适用性分析。而采用尖刀型撞头,外板受力面积较大,双层底结构整体变形较大,一般只有结构相互连接处发生破裂,这种区域常常是有限元分析中的应力集中点,其真实的受力状态可能与实际不符,也不便于进行材料失效准则分析。而圆柱形与球形撞头因为与结构作用面积大,在相同撞头质量与速度情况下,单位面积吸收的能量较低,不容易产生局部破坏。因此,本节采用圆锥形撞头撞击双层壳结构的模型来讨论失效模型的适用性。撞头锥度与尖刀形撞头一致,质量为 400 kg。双层壳结构尺寸不变,分别划分 15 mm,10 mm 和 5 mm 网格,讨论 3 种失效准则的网格敏感性。
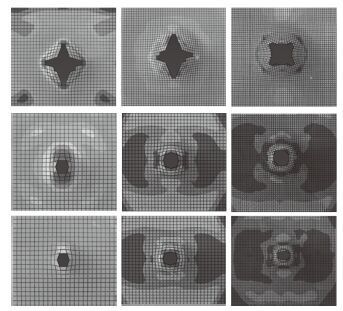
2.3 结果对比图 8 为 3 种失效模型不同网格尺寸下外板的破坏云图。从上到下依次为 GL,RTCL,JC 失效准则的计算结果,从左到右分别为 15 mm,10 mm 和 5 mm 三种不同网格的计算结果。可以看到,在 GL 失效准则下,网格尺寸越大,仿真的裂口尺寸也越大,裂口的边缘越不光滑,但破坏的形式还是比较对称的;RTCL 准则下,10 mm 和 5 mm 网格尺寸下,破裂的尺寸基本相当,而 15 mm 时网格尺寸偏小,只有 2 个单元发生了达到失效条件被删除,破口形状较为对称;JC 准则下,不同网格尺寸下,开口的大小基本相同,网格尺寸越小,开口处的失效单元数越多。
|
图 8 外板撞击破坏图 Fig. 8 Fracture plots of the outer plate |
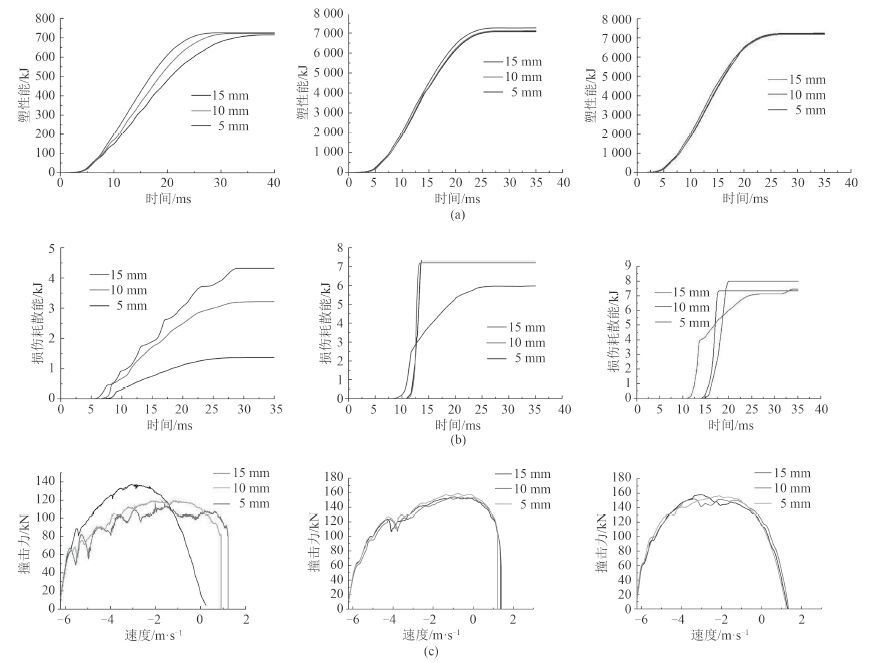
图9分别为 GL,RTCL 和 JC 失效准则下不同网格尺寸时,双层壳结构的变形所吸收的塑性能、损伤耗散能以及撞头冲击力的变化曲线。
|
图 9-1 塑性能、损伤能、撞击力-速度曲线 Fig. 9-1 Curves of plastic dissipation energy damage dissipation energy and force- velocity |
1)对于 GL 失效准则。
① 不同网格尺寸下,最终的塑性吸收能一致,但随时间变化的趋势不同,网格尺寸越小,单元进入塑性越快,其塑性吸收能上升越快。
② 损伤耗散能则随着网格尺寸的增大而变大,这也与破裂缺口的尺寸规律一致。
③ 冲击力峰值随着网格尺寸的减小而增大,而最后撞头的反弹速度随网格尺寸的增大而减小,但不同 FN-V 曲线与坐标轴围成的面积基本相当。这表明整个双层壳结构塑性吸收能基本相当,其对网格尺寸敏感性不强。而局部破坏则表现出对网格的依赖性,但损伤能相比塑性能小。而撞头的接触力随着网格尺寸的精细而增大。
2)对于 RTCL 准则。
① 从结构的塑性能和损伤耗散能来看,10 mm 和5 mm 网格下,塑性能和损伤能都基本一致,而 15 mm网格尺寸下,损伤耗损能相对较小。
② 三种网格下,曲线的峰值和趋势都比较吻合。 说明 RTCL 准则,在网格尺寸小于 10 mm 时,已经具有一定的收敛性。这说明:考虑应力三轴度影响的 RTCL 失效准则对双层壳结构的破坏过程描述是较为准则的。且在 10 mm 网格尺寸下,该准则对网格尺寸的影响不是特别敏感。
3)对于 JC 失效准则。
① 塑性吸收能曲线十分吻合。
② 损伤耗散能最终的值基本相当,但上升趋势有所不同,当网格尺寸为 15 mm 时,从破坏图上来看, 损伤单元的数量较少,曲线上升趋势发生了偏折。
③ 撞头的力-速度曲线基本一致,撞击力在峰值附近有一点波动,但峰值大小基本相当。这说明 JC 失效准则对网格敏感度较小,仿真结果较为准确。
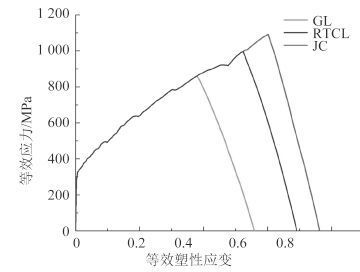
2.4 适用性分析图 10 是 3 种失效准则下,撞击中心单元的等效应力-应变曲线。3 种失效准则发生起始损伤的时间不同,GL 准则最早,RTCL 准则次之,JC 准则最晚,表明 JC 准则所描述的材料延展性更强,不容易发生失效。当损伤发生后的曲线段,3 种失效准则基本保持平行,在这一阶段单元刚度迅速下降,直到完全失效被删除。
|
图 10 中心单元的等效应力-应变曲线 Fig. 10 Equivalent stress-strain curves of the central element |
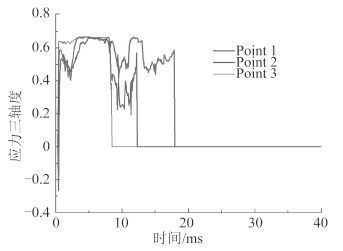
图 11 给出了撞击区域 3 个单元的应力三轴度随时间的变化曲线。撞击区域单元的应力状态比较接近,破坏点单元应力三轴度约在 0.3~0.6 之间。同时也可以看到,越靠近碰撞中心的单元,单元失效越快。
|
图 11 撞击区域 3 个单元的应力三轴度 Fig. 11 Stress triaxiality curves of three elements in the impact area |
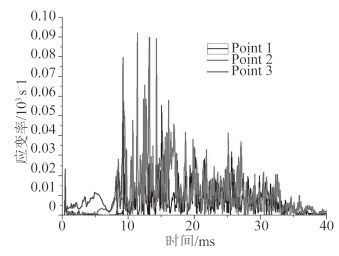
图 12 给出了撞击区域 3 个单元的应变率-时间曲线。可以看出,整个撞击过程中,单元的应变率大都在 102 量级以下,对其进行平均得到的平均应变率为 30 s-1。
|
图 12 撞击区域 3 个单元的应变率曲线 Fig. 12 Strain rate curves of three elements in the impact area |
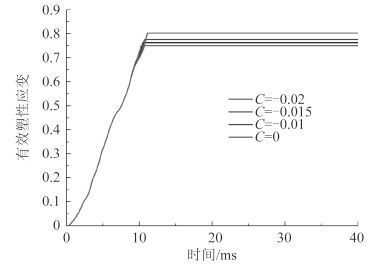
图 13 是不同应变率参数下,撞击中心单元的等效塑性应变曲线。可以看出,在较低应变率下,应变率参数的改变对结果的影响不是很大。因此没有考虑应变率影响的 GL 和 RTCL 失效准则在较细网格下也能对外板的破裂进行较为准确的模拟。
|
图 13 撞击中心单元的等效塑性应变曲线 Fig. 13 Equivalent plastic strain curves of the central element |
本文在已有文献试验数据的基础之上,对典型双层壳结构的碰撞进行了有限元模型和本构模型参数的验证。在此基础之上,采用圆锥形撞头对双层壳结构进行了撞击破坏分析,对比了 GL,RTCL 和 JC 三种失效准则在不同网格尺寸下对撞击破坏的中破口形式、损伤能量和撞击力曲线等影响。由计算结果可以得到:
1) GL 失效准则对网格尺寸较为敏感,需要较精细网格才能够模拟出外板的失效破坏。而 RTCL 失效准则和 JC 失效准则考虑了应力三轴度对断裂失效应变的影响,对网格尺寸的敏感性较小,更加适用于撞击破坏的仿真计算之中。
2)由于板撞击中心破坏区域的应力三轴度在撞击中心变化较小,不考虑应力三轴度的 GL 失效准则也能较好的模拟板的冲击破坏,但相比 RTCL 和 JC 失效准则,其对网格质量的要求更高。同时,低速撞击中,材料的应变率多在 102 量级以下,JC 失效准则中的应变率参数对结果的影响不是很大。
| [1] | HONG L. Simplified analysis and design of ships subjected to collision and grounding[D]. Norwegian University of Science and Technology,2009. |
| [2] | HARIS S, AMDAHL J. An analytical model to assess a ship side during a collision[J]. Ships and Offshore Structures , 2012, 7 (4) :431–448. DOI: 10.1080/17445302.2011.614527 |
| [3] |
温小飞, 卢金树, 崔振东. 船舶碰撞过程的数值模拟及试验研究[J]. 浙江海洋学院学报: 自然科学版 , 2011, 30 (1):71–76.
WEN Xiao-fei, LU Jing-shu, CUI Zhen-dong. Numerical simulation and experimental research of ship collision process[J]. Journal of Zhejiang Ocean University(Natural Science) , 2011, 30 (1) :71–76. |
| [4] | JEN C Y, TAI Y S. Deformation behavior of a stiffened panel subjected to underwater shock loading using the non-linear finite element method[J]. Materials & Design , 2010, 31 (1) :325–335. |
| [5] | MCDERMOTT J F, KLINE R G, JONES E L, et al. Tanker structural analysis for minor collisions[J]. Trans. SNAME , 1974, 82 :382–414. |
| [6] | SUZUKI K, OHTSUBO H, SAJIT C. Evaluation of Absorbed Energy in Collision of Ships-The Effectiveness of Minorsky’s Formula in Anti-Collision Structure[J]. J Soc Naval Architects of Japan , 1999, 186 :311–317. |
| [7] | PAIK J K, CHUNG J Y. On the collision strength of ship’s bow[A]//. Proceeding of the 7th international Offshore and Polar Engineering Conference, Honolulu. 1997: 396-402. |
| [8] | SCHARRER M, ZHANG L, EGGE E D. Final report MTK0614, collision calculations in naval design systems: report Nr. ESS, 2002.183 Version 1/2002-11-22[R]. Germanischer Lloyd, Hamburg, 2002. |
| [9] | RICE J R, TRACEY D M. On the ductile enlargement of voids in triaxial stress fields[J]. Journal of the Mechanics and Physics of Solids , 1969, 17 :201–217. DOI: 10.1016/0022-5096(69)90033-7 |
| [10] | PESCHMANN J, KULZEP A. Final report for BMBF Life-Cycle Design. Part D2A: Side collision of double skin ships[R]. Technical University of Hamburg, 2000. |
| [11] | JOHMSON G R, COOK W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures[J]. Engineering Fracture Mechanics , 1985, 21 (1) :31–48. DOI: 10.1016/0013-7944(85)90052-9 |
| [12] | VILLAVICENCIO R, KIM Y H, CHO S R, et al. Deformation process of web girders in small-scale tanker double hull structures subjected to lateral impact[J]. Marine Structures , 2013, 32 (3) :84–112. |
| [13] | 孔祥韶. 爆炸载荷及复合多层防护结构响应特性研究[D]. 武汉:武汉理工大学, 2013. |
 2017, Vol. 39
2017, Vol. 39
