随着科学技术与机械制造水平的发展,机械设备向着精细化、复杂化、智能化、高效化的方向不断发展。设备在运行过程中的状态可靠性、安全性等问题得到逐渐重视[1]。通过对往复泵振动信号的特点进行分析,发现其振动信号极其具有复杂性和不确定性,为了更精确的进行基于振动信号的故障诊断,有必要对往复式舱底泵进行故障机理的研究,分析泵体表面振动信号的本质特性,掌握振动在泵体结构中的产生机理和传递路径,建立表面振动信号与内部运动机构磨损等因素的内在联系,对设备状态监测和故障诊断方法的选取,特征参量和诊断标准的制定具有重要意义[2]。
往复泵运动机构磨损是影响其性能的主要因素,本文以双缸双作用往复泵为研究对象,对磨损故障机理进行分析,采用接触-分离 2 种状态模型建模方法[3],将磨损故障模型简化为运动副之间的运动间隙,从而建立曲柄-连杆磨损的动力学模型。在建模过程中,综合考虑了往复泵的实际工作状态、各构件之间的相互关系以及流体脉动现象。通过数值求解与 ADAMS 联合仿真,分析磨损间隙变化与动力学响应之间的相互关系,为往复泵故障检测与诊断分析提供理论依据。
1 往复泵力学模型分析某型双缸双作用往复泵结构如图 1 所示。设备由传动部件和液体输出部件 2 部分组成,其中传动部件由机体、齿轮传动装置、曲轴和曲柄机构组成;液体输出部件由活塞组件、吸排阀组件、压力罩等组成。往复泵的工作原理是容变,阀箱内有吸入阀和排出阀,工作时依靠阀门两边压差自动打开和关闭阀门,当活塞在水缸内往复运动时,工作室的容积发生变化,在工作室内外产生压差,在吸排阀的配合下吸排液体。本文通过研究建立往复泵曲柄机构振动系统分析方法和计算模型,分析部件间隙状态变化对机组振动噪声性能的影响。在建模计算过程中,忽略电机、涡轮和轴承对曲柄连杆机构振动的影响,主要分析磨损间隙和活塞的压力变化情况对泵的振动特性影响变化,并根据实际情况添加约束条件。
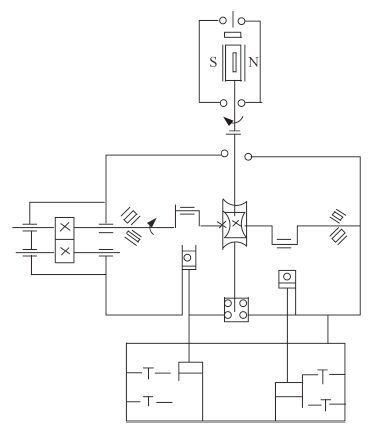
|
图 1 往复泵传动系统示意图 Fig. 1 Reciprocating bilge pump drive system |
通过接触—分离二状态模型建立往复式舱底泵的运动副磨损动力学方程,并以曲柄连杆机构运动副的磨损间隙为例进行具体的推导分析[4]。
2.1 连杆动力学方程取连杆为研究对象,对其单独进行受力分析[5],图 2 为带间隙的受力图,得到其动力学方程如下:
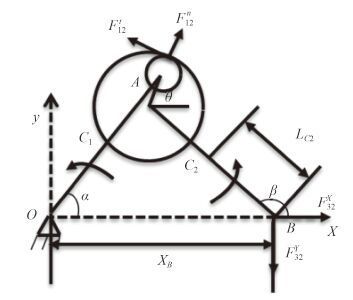
|
图 2 曲柄连杆机构受力分析 Fig. 2 Crank mechanism mechanical analysis |
| $ {m_2}{\ddot x_{{c_2}}} = F_{12}^n\cos \theta- F_{12}^t\sin \theta + F_{32}^x{,} $ | (1) |
| $ {m_2}{\ddot y_{{c_2}}} = F_{12}^n\sin \theta + F_{12}^t\cos \theta- F_{32}^y- {m_2}g{。} $ | (2) |
式中:
对B 点取矩,由动量矩守恒定理有:
| $ \begin{array}{l} {J_B}\ddot \beta = F_{12}^t[{L_2}\cos \left( {\beta- \theta } \right) + {R_A}]- F_{12}^n{L_2}\sin \left( {\beta- \theta } \right)+\\ \quad\quad\quad {m_2}g{L_{{c_2}}}\cos \beta + {m_2}{{\ddot x}_B}{L_{{c_2}}}\sin \beta \end{array} $ | (3) |
式中:JB 为杆件对B 点的转动惯量;RA 为处轴套半径轴承内圈半径。
根据构件之间的几何关系有:
| $ {x_{{c_2}}} = {x_B}- {L_{{c_2}}}\cos \beta{,} $ | (4) |
| $ {y_{{c_2}}} = {L_{{c_2}}}\sin \beta{。} $ | (5) |
对上式求微分可得:
| $ {\ddot x_{{c_2}}} = {\ddot x_B}- {\dot \beta ^2}{L_{{c_2}}}\cos \beta + \ddot \beta {L_{{c_2}}}\sin \beta {,} $ | (6) |
| $ {\ddot y_{{c_2}}} =- {\dot \beta ^2}{L_{{c_2}}}\sin \beta- \ddot \beta {L_{{c_2}}}\cos \beta {,} $ | (7) |
采用二状态接触模型进行建模,由构件的几何关系:
| $ {d_x} = {L_1}\cos \alpha- {L_2}\cos \beta- {x_B}{,} $ | (8) |
| $ {d_y} = {L_1}\sin \alpha- {L_2}\sin \beta {,} $ | (9) |
式中dx 和dy 为轴销与轴套在x 与y 方向的相对位移。
从而可以得到接触点处轴销与轴套的相对切向和法相速度:
| $ v_{12}^t = {\dot d_y}\cos \theta- {\dot d_x} + \sin \theta \left( {\dot \alpha- \dot \beta } \right){r_A}{,} $ | (10) |
| $ v_{12}^n = {\dot d_y}\sin \theta + {\dot d_x}\cos \theta {。} $ | (11) |
式中rA 为轴销半径。
用接触分离二状态方程解上述方程,令法向接触变形为σ,磨损间隙为δ,轴销与轴套的相对位移为d,所以有:
σ=d-δ
引入阶跃函数:
| $\mu \left( \sigma \right)\text{=}\left\{ \begin{matrix} 1, & \sigma \ge 0, \\ 0, & \sigma <0, \\ \end{matrix} \right.$ |
由二状态接触碰撞模型方程[6]:
| $ F_{12}^n = \left( {K{\rm{\sigma }} + {C_n}v_{12}^n} \right)\mu \left( {\rm{\sigma }} \right){,} $ | (12) |
| $ F_{12}^t =- \left( {fsign\left( {v_{12}^t} \right)} \right)F_{12}^n + {C_t}v_{12}^t)\mu \left( {\rm{\sigma }} \right){,} $ | (13) |
式中K 为轴套刚度系数;Cn 为法向阻尼系数;Ct 为切向阻尼系数;f为库伦摩擦系数。
则间隙碰撞力在X 和Y 方向的力分别为:
| $ {F_{AX}} = \mu \left( {\rm{\sigma }} \right)\left( {- F_{12}^t\sin \theta + F_{12}^n\cos \theta } \right){,} $ | (14) |
| $ {F_{AY}} = \mu \left( {\rm{\sigma }} \right)\left( {F_{12}^t\cos \theta + F_{12}^n\sin \theta } \right){。} $ | (15) |
往复式舱底泵在工作过程中,曲柄连杆机构在曲轴的带动下进行周期性的运转,活塞随之进行往复运动,所以作用在活塞上的流量也是随之周期性变化的,将会对活塞表面产生脉动压力,对机体振动也将产生显著影响。在计算往复泵流量时,由于流量相对较大,可以忽略运动副间的磨损间隙对流量变化产生的影响[7]。如图 2 所示机构模型,忽略运动副间的间隙影响进行流量计算。
活塞往复运动的位移为:
| $ {{\rm{x}}_B} = {L_1} + {L_2}- \left( {{L_1}\cos \alpha + {L_2}\cos \beta } \right){,} $ | (16) |
式中:L1 为曲柄长度;L2 为连杆长度。
由构件的几何关系有:
| $\cos \beta =\sqrt{1-{{\lambda }^{2}}{{\sin }^{2}}a}$ |
式中:
将其带入上式可得:
| $ \begin{array}{l} {x_B} = {L_1}\left( {1- \cos \alpha } \right) + {L_2}\left( {1- \sqrt {1- {\lambda ^2}{{\sin }^2}\alpha } } \right),\;\\ \alpha = \omega t{。} \end{array} $ | (17) |
式中ω 为曲柄转速。
由于 λ 的值很小可以忽略不计,
| $ {{{Q}}_1} = {{A}}{{\rm{\dot x}}_B} = A{L_1}\omega \left( {\sin \alpha + \frac{{\lambda \sin 2\alpha }}{2}} \right) \approx A{L_1}\omega \sin \alpha {。} $ | (18) |
由上面计算推导出的公式可知单缸单作用往复泵的理论流量以正弦函数脉动。双缸双作用泵是以上单缸单作用的叠加,相位差为 180°。
2.2.2 压力计算1)吸入压力计算
在图 3 中,取 1 号和 2 号缸与活塞的液体接触端处的截面为 1-1,在单位时间内通过截面 1-1 的液体总能量为:
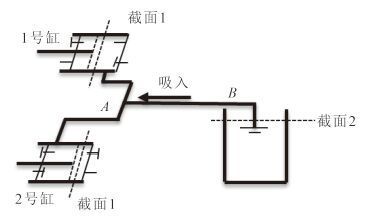
|
图 3 舱底泵工作原理图 Fig. 3 Bilge pump working principles |
| $ {E_{1- 1}} = \rho {Q_1}{Z_1} + {P_1}{Q_1}/{\text{g}} + \rho {Q_1}\mu _1^2/2{\text{g}}{。} $ | (19) |
式中:Q1 为经过截面 1-1 的流量;ρ 为液体密度;μ1 为流体速度。
取液缸的液面为截面 2-2,在单位时间内通过截面 2-2 的液体总能量为:
| $ {E_{2- 2}} = \rho {Q_1}{Z_0} + {P_a}{Q_1}/{\text{g}}{,} $ | (20) |
根据往复泵的能量平衡方程式有:
| $ {E_{1- 1}} + {E_{BA}} + {E_{A1}} = {E_{2- 2}}{。} $ | (21) |
式中:EBA 为 1 号液缸在单位时间内吸入的液体流经总管BA 段的能量损失;EA1 为 1 号液缸在单位时间内吸入的液体流经支管A1 段的能量损失。
定义单位质量的液体在BA 段、A1 段的比能分别为hBA 和hA1 ,则有:
| $ {E_{BA}} = \rho {Q_1}{h_{BA}}{,} $ | (22) |
| $ {E_{A1}} = \rho {Q_1}{h_{A1}}{。} $ | (23) |
将以上各式带入能量平衡方程有:
| $ \rho {Z_1} + {P_1}/g + \rho \mu _1^2/2g + \rho {h_{BA}} + \rho {h_{A1}} = \rho {Z_0} + {P_a}/g{,} $ | (24) |
从而可以得到:
| $ \begin{aligned} {P_1} = & {P_a} + \rho {Z_0}g-\\ & \left( {\rho {Z_1}g + {P_1} + \rho \mu _1^2/2 + \rho {h_{BA}}g + \rho {h_{A1}}g} \right){。} \end{aligned} $ | (25) |
令:
| $ {{{P}}_1}\!=\!{{{P}}_{{a}}}\!+\!{{\rho }}{{{Z}}_0}{{g}}\!-\!{{\rho g}}\left( {{{{Z}}_1} \!+\! {{{h}}_{{阻}1}} \!+\! {{{h}}_{{{惯}}1}}\!+\! {{{K}}_{{阻}1}} \!\!+\!\! {{{K}}_{{{惯}}1}}} \right)\!-\!{{{P}}_1}\!-\!{{\rho \mu }}_1^2/2{。} $ | (26) |
式中:h阻1 为吸入流道内液流的总阻力损失;h惯1 为吸入流道内液流的总惯性压头;K阻1 为吸入阀的阻力损失;K惯1 为吸入阀的惯性压头;Z1 为 1-1 截面高度;Z0 为 2-2 截面高度
将各项参数带入上式,运用 Matlab 计算,可以得到吸入压力的曲线图(见图 4)。
2)压力计算
排出过程中,舱底泵的活塞压缩缸内液体,使缸内液体压力升高,从而克服液体在排出过程中的惯性力、流动阻力和背压,以及出口阀的惯性力与阻力,使液体排出机体,并具有一定的排出速度,根据上述推导液体吸入压力的过程,可以推导出排出过程的能量平衡方程:
| $ \begin{aligned} {P_2} = &{P_c} + \rho {Z_c}g + \rho \mu _c^2/2- \rho \mu _2^2/2 + \\ &\rho g\left( {{h_{{{阻}}2}} + {h_{{{惯}}2}} + {K_{{{阻}}2}} + {K_{{{惯}}2}}} \right) \end{aligned} $ | (27) |
式中:h阻2 为排出管中的总阻力损失;h惯2 为排出管中的总惯性压头;K阻2 为排出阀的阻力损失;K惯2 为排出阀的惯性压头;P2 为排出过程中缸内压力;Pc 为排出管出口端液体压力;Zc 为排出口距液缸中心高度;μc 为排出管端液体的流速;μ2 为泵的输入压力
同上述吸入压力的计算过程,利用 Matlab 可以得到泵的排出压力曲线图。
3)缸内综合压力
3 仿真计算双缸双作用往复泵两缸始终处于吸入、排出阶段,所以缸内压力为上述吸入排出压力的矢量和。综合上述计算得到的吸入、排出压力曲线,可以得到其综合压力如图 4 所示。
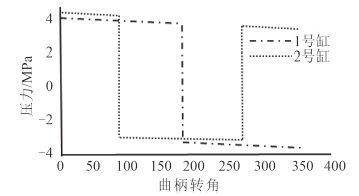
|
图 4 综合压力曲线 Fig. 4 Integrated pressure curve |
在以上理论计算推导的基础上,运用 Matlab 和 ADAMS 进行联合仿真验证[8],曲柄连杆机构计算所需要的模型参数为活塞直径 85 mm,活塞行程 104 mm,活塞长度 55 mm,连杆直径 32 mm,连杆长度 300 mm。
|
|
表 1 曲柄连杆机构基本参数 Tab.1 Crank-link Mechanism Basic Parameter |
分别对曲柄连杆机构运动副处在有间隙和无间隙状态进行仿真对比分析,根据舱底泵的实际工作情况加载作用力和边界条件,并对曲柄进行了柔性处理,并充分考虑各个部件的接触关系和受力关系。仿真结果图 5 ~图 7 所示。
|
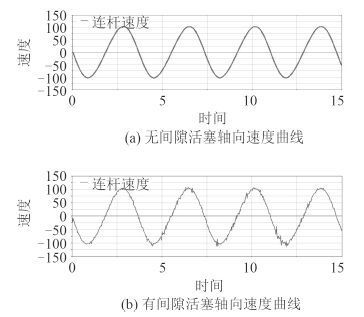
图 5 活塞轴向速度曲线 Fig. 5 Velocity curve between the piston |
|
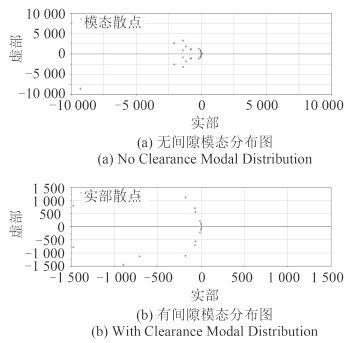
图 6 模态分布图 Fig. 6 Modal Distribution |
|
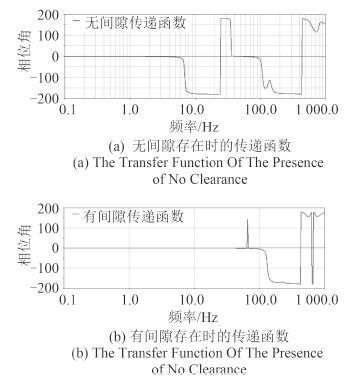
图 7 传递函数 Fig. 7 The Transfer Function |
由图 5 可看出,运动副处存在间隙时,活塞的速度曲线不再是光滑的,速度曲线在小范围内存在波动,这些波动会加剧活塞的不规则运动,加大流量和压力的脉动,从而会加剧活塞的振动,同时也会对机体振动会造成很大影响。
由图 6 可看出,在运动副处存在磨损间隙的情况时,运动机构的模态分布更为分散。从而造成在不同的工作范围内,在机构存在磨损间隙的情况下,舱底泵工作时更容易引起机体的共振,从而加剧机体振动。
由图 7 可看出,无间隙存在时,机构的传递函数更为稳定,所以更加有易于对机体振动噪声进行控制。存在间隙后,传递函数更趋于无规则性,加大了诊断难度。
4 结语本文通过对双缸双作用往复式舱底泵的研究,计算出了其工作时的流量和压力变化情况。然后利用接触—碰撞二状态模型建立了曲柄连杆机构存在磨损间隙时的动力学和运动学方程。最后结合往复泵的实际接触关系、工作情况和上面得到的压力变化,利用 Adams 进行了运动学、动力学和振动仿真,对比了运动副有无间隙情况下的运动和振动特性。得到了以下结论:
1)通过建立舱底泵的流量和压力方程,得到了舱底泵工作时的综合压力曲线,为以后的往复式泵的压力计算提供了方法。
2)建立了运动副存在间隙情况下的接触—碰撞模型,模拟了曲柄连杆机构磨损的故障情况,为以后的磨损机体研究提供了新思路。
3)结合 Matlab 和 Adams 进行联合仿真,将用 Matlab 得到的压力曲线和受力曲线导入 Adams 模型中作为工况条件,使仿真更加符合实际情况。
4)运用 Adams 自带的振动分析模块,对模型进行了振动分析,为以后的振动机理研究提供了方法,弥补了实验难的问题,同时也得到了运动副存在磨损时,会显著影响机体的振动特性。在以后的研究中,可以通过改变运动副的间隙情况和接触情况,模拟不同情况下的振动特性,然后与已经测得的数据进行对比,为设备的故障诊断提供依据。
| [1] | BAUCHAU O A, RODRIGUEZ J. Modeling of joints with clearance in flexible multi-body systems[J]. International Journal of Solids and Structures , 2002, 39 (1) :41–63. DOI: 10.1016/S0020-7683(01)00186-X |
| [2] | FLORES P, AMBRÓSIO J, CLARO J C P. Influence of the contact—impact force model on the dynamic response of multi-body systems[J]. Influence of the contact—impact force model on the dynamic response of multi-body systems , 2006, 220 (1) :21–34. |
| [3] | DONG Fu-xiang, HONG Jia-zhen. Review of impact problem for dynamics of multibody system[J]. Advances in Mechanics , 2009, 39 (3) :352–359. |
| [4] | BAI Zheng-feng, ZHAO Yang, ZHAO Zhi-gang. Dynamic characteristics of mechanisms with joint clearance[J]. Dynamic characteristics of mechanisms with joint clearance , 2011, 30 (11) :17–20, 41. |
| [5] | TIAN Hao, KOU Wei, BAI Zheng-feng. Effects analysis of clearance on kinetic characteristic of plane mechanism[J]. Machinery Design & Manufacture , 2010, 20 (2) :17–18. |
| [6] | KOSHY C S. Characterization of mechanical systems with real Joints and flexible links[D]. Wichita, KS: Wichita State University, 2006. |
| [7] | QU Xiu-quan. Dynamic simulation of planar linkage based on MATLAB/Simulink[M]. Harbin: Harbin Institute of Technology Press, 2007: 38-92. |
| [8] | LI Zeng-gang. ADAMS detailed introduction and examples[M]. 2nd ed. Beijing: National Defense Industry Press, 2014. |
 2017, Vol. 39
2017, Vol. 39
