随着经济全球化进程加快,原油需求量不断增加,作为原油运输主要载体的油船受到广泛关注。针对油船结构进行结构优化,减少船体钢材的使用,降低建造成本,对提高油船产品的竞争力具有十分重要的工程意义。
船舶结构优化设计方法主要可分为规范方法和直接计算方法 2 种[1]。基于有限元分析的优化方案逐渐成为了一种新的船舶结构优化设计模式,很多学者在这方面进行了相关的研究[2-6]。在利用直接计算法对船舶结构进行优化的过程中,为了准确地求出结构响应,通常需要大量的有限元分析计算过程。而伴随着工程结构逐渐向着复杂与庞大方向发展,有限元模型规模也变得更加庞大与精细。从而也会导致有限元分析时间变长,使整个优化过程效率降低。通过根据试验设计思想,采用具有代表性的样本数据,构造出神经网络数学模型,并将神经网络模型作为有限元分析的替代模型,来表达输入参数与结构响应之间的关系,可大幅度减少有限元分析次数提高优化效率,成为了结构优化设计的新趋势[7-9]。
本文主要针对采用 BP 神经网络来构建神经网络模型时,存在易陷入局部最小值、稳定性差的问题,利用粒子群算法对 BP 神经网络模型进行优化改进,并将基于粒子群优化的 BP 神经网络模型对油船舱段结构进行优化,并对优化后的结果进行验证分析。
1 优化方案 1.1 设计变量选取大型油船舱段结构复杂,参数变量较多,考虑到有限元分析、建模以及优化过程的效率等。并没有将所有构件都作为设计变量进行分析,其中骨材型号、骨材间距等作为已知量。采用参数试验法对变量进行灵敏度分析,从而确定优化过程中涉及到的设计变量。
1.2 约束条件以文献[10]中相关规定,确定各构件的几何约束条件,船舶所受到的等效应力、剪应力最大值约束限制如下:
| $ {\sigma _{\max }} \leqslant \left[ \sigma \right], $ | (1) |
| $ {\tau _{\max }} \leqslant \left[ \tau \right]。 $ | (2) |
σmax和τmax 通过调用 PSO-BP 神经网络拟合的剪应力板厚函数关系来确定。
1.3 目标函数以油船舱段重量最轻为优化目标,数学表达式为:
| $ F\left( X \right) = \sum\limits_{i = 1}^n {{\rho _i}{V_i}} = \sum\limits_{i = 1}^n {{\rho _i}{S_i}{t_i}} 。 $ | (3) |
式中:ρi 为不同构件的材料密度;n 为构件数量;Vi 为第i 个构件体积;Si 为第i 个构件面积;ti 为第i 个构件厚度。
2 有限元分析本文以 1 艘载重量 107 500 DWT 的阿芙拉型油船为研究对象。该船为双底、双舷侧、单甲板的船体结构,全船采用纵骨架式结构,设有一道中纵舱壁以及 5 道横舱壁。有限元分析时采取货舱中部 1/2 + 1 + 1/2 三舱段模型。按照计算工况对舱段进行有限元分析,并对其中较为危险的工况计算结果进行整理,部分计算结果如图 1 所示。

|
图 1 应力云图 Fig. 1 Stress nephogram |
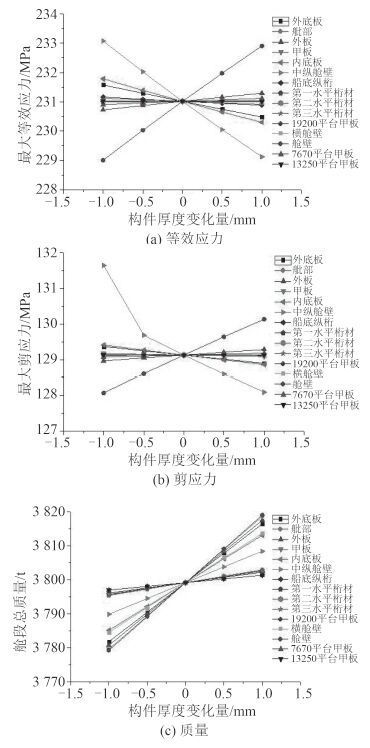
利用 Nastran 软件来计算改变舱段各个构件参数后舱段的等效应力最大值、剪应力最大值的响应结果以及改变各个构件参数后舱段质量变化。利用参数试验方法对数据进行灵敏度分析,并对计算结果进行数据分析与整理,如图 2 所示。
|
图 2 灵敏度分析结果 Fig. 2 Results of sensitivity analysis |
对图 2 结果进行分析,将变量中对等效应力最大值、剪应力最大值、质量等影响较小的因子剔除,可以看出,中纵舱壁、内壳板、内底板、外底板、外板、甲板等构件对等效应力最大值、剪应力最大值、质量等影响较为明显。从而将其作为有效设计变量。
4 PSO-BP 神经网络构建利用 Matlab 软件建立了反映等效应力最大值、剪应力最大值与设计变量映射关系的 BP 神经网络,并对网络进行了训练与检验,发现 BP 神经网络存在易陷入局部最小值,误差不稳定等问题。针对 BP 神经网络的不足与缺陷,提出一种基于粒子群算法的 BP 神经网络结构模型,来解决易陷入局部极值等问题。
4.1 结构设计将中纵舱壁、内壳板、内底板、外底板、外板、甲板等构件的厚度变量作为输入,将等效应力最大值、剪应力最大值等作为输出。构建 2 个 6-13-1 的单隐层 PSO-BP 神经网络。训练样本与测试样本等都采用利用正交试验进行有限元分析所得到的数据,数据共 150 组,其中 125 组用作训练样本,25 组作为检测样本。
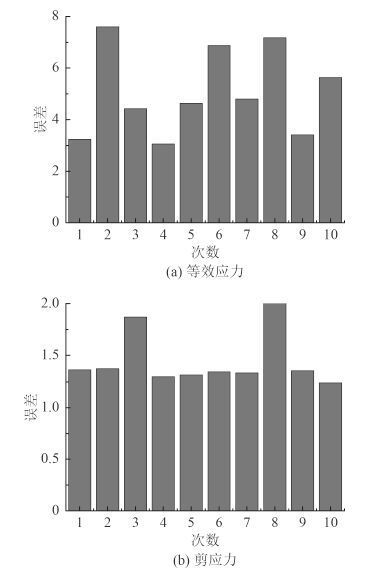
4.2 训练结果对构建的 PSO-BP 神经网络模型进行 10 次神经网络训练运算,每次迭代最大次数同样为 5 000 次,误差值为 10E-5,学习速率设置为 0.1。将每次的测试结果进行统计,误差情况见图 3。
|
图 3 测试误差 Fig. 3 Test error |
由图 3(a) 中舱段等效应力最大值与板厚的 PSO-BP 神经网络的训练结果可以看出,10 个不同的 PSO-BP 神经网络模型均完成了训练过程,且其中 5 个模型的总误差值在 5 以下,而最高的误差情况为 7.60,这 10 个模型总误差维持在 5 左右。从图 3(b) 中舱段剪应力最大值与板厚的 PSO-BP 神经网络训练结果中可以看出,10 个不同的 PSO-BP 神经网络模型总误差值维持在了 1.5 左右,误差值较小。可见本文构建的 PSO-BP 神经网络模型精度较高,全局寻优能力强,且整体稳定性十分良好。
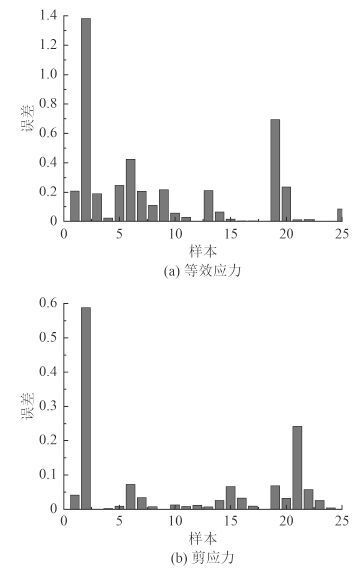
4.3 泛化能力检测对 PSO-BP 神经网络模型的泛化能力进行检测,测试误差结果如图 4 所示。
|
图 4 PSO-BP 测试样本误差 Fig. 4 PSO-BP test sample error |
从图 4 结果可看出,应力 PSO-BP 神经网络模型的大部分样本误差值都在 0.5 以下,最大为 1.4;剪应力 PSO-BP 神经网络的大部分样本误差值都在 0.3 以下,最大为 0.6,PSO-BP 神经网络的预测数据与期望数据的拟合程度较好,精度高。PSO-BP 网络的泛化能力更强,也更加稳定,能够作为有效的有限元分析过程的代理模型,参与到优化过程中。
5 优化结果及分析将中纵舱壁、内壳板、内底板、外底板、外板、甲板等构件作为优化过程中的设计变量,利用 PSO-BP 神经网络的预测的板厚与应力、剪应力的非线性函数对其进行约束,以大型油船舱段重量最轻为优化目标,进行结构优化,各设计变量厚度优化后结果如表 1所示。优化后模型质量从 3 799 t 降为 3 640 t,质量减少了 4.2% 左右。
|
|
表 1 优化前后结果/mm Tab.1 The optimized and optimized results/mm |
利用上一节优化结果对有限元模型进行参数修改,对修改后的舱段模型进行有限元分析,分析结果如图 5 所示。

|
图 5 舱段应力云图 Fig. 5 Cabin stress nephogram |
图 5 给出的有限元分析结果表明,优化后等效应力、剪应力等满足设计规范要求。
6 结语根据优化设计理论,建立了舱段结构优化模型。以舱段质量为目标函数,以相关规范要求的板厚与应力为约束条件,通过调用 PSO-BP 神经网络代替有限元分析,对舱段进行了结构优化。优化后舱段质量降低了 4.2%。并将优化后的结果进行了有限元分析,分析结果表明满足规范要求,证明了 PSO-BP 神经网络模型在船舶结构优化设计中的可行性。
| [1] |
俞铭华, 嵇春艳, 管义锋. 大型油船结构优化设计研究进展[J]. 江苏科技大学学报(自然科学版) , 2006 (2):1–6.
YU Ming-hua, JI Chun-yan, GUAN Yi-feng. Advances in Structural Optimum Design of Large Crude Oil Carriers[J]. Journal of Jiangsu University of Science and Technology(Natural Science Edition) , 2006 (2) :1–6. |
| [2] | 李仲伟, 吴有生, 崔维成. 基于有限元法的小水线面双体船结构优化[J]. 船舶力学, 2005(2): 99-108. |
| [3] | 张丽. 巴拿马型集装箱船结构优化设计研究[D]. 上海: 上海交通大学, 2008. |
| [4] |
潘彬彬, 崔维成. 基于有限元的整船结构多学科设计优化[J]. 中国造船 , 2010, 01 :47–54.
PAN Bin-bin, CUI Wei-cheng. FEM Based MDO Model for Entire Ship Structural Optimization[J]. FEM based MDO model for entire ship structural optimization , 2010, 01 :47–54. |
| [5] | KARR D G., BEIER K P, LEE K D. A framework for simulation-based design of ship structures[J]. Journal of Ship Production , 2002, 18 (1) :33–46. |
| [6] | ZANIC V, JANCIJEV T, TRINCAS G. Structural design methodology for large ships[J]. Journal of Ship and Ocean Technology , 2001, 5 (1) :14–29. |
| [7] |
程远胜, 孙莹, 闫国强. 基于神经网络与遗传算法的潜艇舱壁结构优化[J]. 中国造船 , 2008, 04 :81–87.
CHENG Yuan-sheng, SUN Ying, YAN Guo-qiang. Structural Optimization of a Submarine End Plane Transverse Bulkhead Based on Neural Networks and Genetic Algorithm[J]. Structural optimization of a submarine end plane transverse bulkhead based on neural networks and genetic algorithm , 2008, 04 :81–87. |
| [8] | UN L, WANG D Y. Optimal structural design of the midship of a VLCC based on the strategy integrating SVM and GA[J]. Optimal structural design of the midship of a VLCC based on the strategy integrating SVM and GA , 2012 (11) :59–67. |
| [9] | 邓良. 基于人工神经网络的船舶结构轻量化研究[D]. 济南: 济南大学, 2014. |
| [10] | 中国船级社. 钢制海船入级规范[S]. 北京: 人民交通出版社, 2012. |
 2017, Vol. 39
2017, Vol. 39
