船体长期处于海水环境中,其外板与海水直接接触。由于船用油漆涂料保护层的作用,长时间后板格表面实际则形成了许多大小不同的腐蚀坑。对于一些有一定使用年限的老龄船舶,整个船体包括有均匀腐蚀、非均匀腐蚀、局部腐蚀等多种腐蚀情况。板格作为船体结构的基本构件之一,其强度性能是强度校核以及船舶检修时重要的评估指标。在以往的一些研究中,对腐蚀后的板厚一般处理成均匀腐蚀即等效成相应的板厚。随着对船体钢结构腐蚀的研究发现,对于船底外板主要是坑点腐蚀比较严重。由于点腐蚀的复杂性,至今行业内都仍然没有公认、统一的评估方法。近年来,国内外学者提出了一些相应的腐蚀模型以及评估方法。韩国专家 Paik[1]利用试验与有限元结合的方法对有点腐蚀的钢板进行了极限强度分析,表明单点腐蚀对整个钢板的极限强度影响很小。Paik[2]将点蚀面积作为点蚀损伤的参考要素,并且经过数值分析得到了量化公式。Dunbar[3]采用有限元方法分析了坑点腐蚀对船舶结构中的典型板构件和加筋板构件的影响。Nakai等[4]对轴向受压的板进行了研究,认为有规则的点蚀坑对板结构的极限强度影响小于或几乎等于均匀腐蚀的情况。王燕舞等[5]对四边简支板进行轴向压缩试验与 Ansys 非线性有限元分析,得出的结论是四边简支点腐蚀板极限强度与其板面腐蚀面积无直接联系,腐蚀体积是极限强度的主要控制因素。并且拟合出了极限强度比 Rxu 与板损失体积比(Vloss /V0)的关系函数。江晓俐等[6]采用非线性有限元法对未穿透低碳钢板进行分析,研究表明点腐蚀坑深度的改变会造成板的极限承载能力有很大差异,同时认为在采用点腐蚀密集度参数 DOP 表征点腐蚀破坏程度有所不足,应考虑薄壁效应。张岩等[7]基于腐蚀体积描述点腐蚀损伤程度,通过改变板厚、蚀坑直径以及蚀坑分布,运用有限元数值软件进行模拟计算和分析,提出了基于腐蚀体积的点蚀损伤板极限剪切屈曲强度的计算公式。船舶在海洋里航行过程中会遭受静水压力,波浪弯矩以及风荷载等各种形式荷载的联合作用。因此,计算船体板结构在复杂荷载作用下的极限强度具有十分重要的工程意义。
1 非线性有限元分析 1.1 计算模型本文运用 Ansys 进行非线性分析,采用 shell181 单元模拟单侧点腐蚀损伤板,为更加真实反映出实际情况,蚀坑模拟采用节点偏置的方法。现取一船体板格长边a = 1 000 mm,短边b = 500 mm,厚度t = 12 mm;材料属性为:弹性模量E = 205.8 GPa,泊松比v = 0.3,屈服应力为σ = 235 MPa。有限元模型中蚀坑的模拟使用圆柱形且均匀分布于板面上,因考虑板格一侧在海水中会受静水压力的直接作用,本文将船底板侧向水压载荷取为 0.16 MPa 近似模拟在水中的压强。边界条件为四边简支且在到达极限强度之前,板边保持直边变形。施加 1 阶特征值屈曲模态作为板面的初始变形,其幅值w =b/200。暂不考虑焊接残余应力的影响。整个板模型中网格大小均按 10*10 划分,蚀坑部分的网格采用放射状划分。
1.2 方法验证国内外专家、学者对四边简支矩形板的理论研究比较成熟,推导出了计算光板极限强度的理论公式。其中 Faulkner 公式由于与试验数据吻合的比较好,被广泛应用。因此,采用本文的有限元方法计算不同尺寸板格的极限强度与 Faulkner 公式的理论值进行对比,验证计算方法的准确性。
Faulkner 公式:
| $ \frac{{{\sigma _u}}}{{{\sigma _y}}} = \frac{2}{\beta }- \frac{1}{{{\beta ^2}}}。 $ | (1) |
通过表 1 可发现,本文所采用的数值计算方法结果与理论公式的计算值误差控制在 5% 之内,能够很好地与公式中的计算结果相吻合,表明后续的数值计算采用该方法真实可信。
|
|
表 1 公式与数值分析结果对比 Tab.1 The comparison of the results of nummerical calculation and formula |
在现有文献中,在计算板的极限强度时主要是在单轴向或者双轴向施加压力,并未涉及到侧向压力的作用。本节通过施加不同的侧向载荷来分析其所带来的强度影响。蚀坑的相关参数仍然与前面相同,侧向载荷大小依次取 0,0.04,0.08,0.12,0.16 MPa。
根据表 2 计算结果可知,板的纵向极限强度随着侧向载荷的增加有着明显的下降。当只有单向轴向压力作用时,强度的变化最大只有 5.5%,而对于双轴向加上侧压情况时,强度变化率分别为 8.9%,9.5%,9.57%。这说明边缘载荷比对强度有重要影响。计及侧压比忽略侧压的强度值减小了 16.8%,32.4%,特别的是当双轴向都受压时,侧向载荷对强度的影响比单轴受压时更加显著。
|
|
表 2 不同侧压下的计算结果 Tab.2 The calculation results of different pressure |
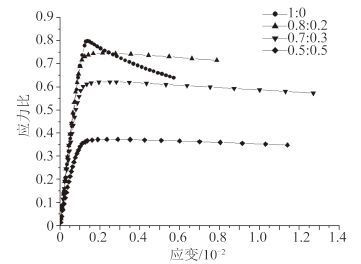
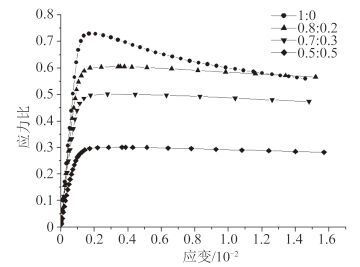
船体在航行过程中可能会遭受各种各样的海况,长短边受到的应力水平是不一样的。因此,为考察长边与短边的载荷比例对点腐蚀板材的极限强度影响。现假定腐蚀坑圆柱直径为 30 mm,腐蚀面积与原板面积比例为 5.08%(即蚀坑数目为 4*9 模型),蚀坑的腐蚀深度取为 0.5*t,分析了 4 种工况下板的极限强度。图 2 为表面未腐蚀板材在不同边缘载荷系数下的 Von Mises 应力应变曲线。图 3 为含有腐蚀缺陷的情况下薄板的 Von Mises 应力应变曲线图。
|
图 1 应力-应变曲线图 Fig. 1 The curve graph of stress-strain |
|
图 2 应力-应变曲线图 Fig. 2 The curve graph of stress-strain |
从图 4 可发现,随着边缘荷载系数比的增大,薄板的极限压缩强度是越来越小,完整板与腐蚀板强度变化的趋势是相近的。在图 3 中,对于板格有腐蚀缺陷时,在各种工况下的极限强度都有不同程度的下降,然而腐蚀对板格的后屈曲强度的影响程度很小,与完整板无异。图 2 和图 3 表明对于 2 种不同状态的薄板,横向载荷都能够“延缓”板的后极限强度变化速度。当载荷比为 1:0 时,完整板在达到极限值之后随着应变的增加 Von Mises 应力较腐蚀后变化快。无论是腐蚀前还是腐蚀后,边缘的载荷比对板的极限抗压强度影响有着不可忽略的影响。腐蚀仅对极限承载力有所影响,对板的后极限强度并无影响。
|
图 3 边缘载荷比的影响 Fig. 3 Influence of ratio of edge load |
为了研究含多蚀坑船底板在复杂荷载状态下的极限强度影响因素,本节重点讨论蚀坑的几何参数对极限强度的影响。由于在实际工作过程中,主要承受纵向压力。因此暂取长边与短边压力比为 0.3 : 0.7 的作为工作状态。船底板因长期与海水接触,在其表面所形成的蚀坑也都是形态各异。因此,蚀坑的几何参数对板强度的影响程度也是在船体结构进行强度评估时候重要的参考因素。
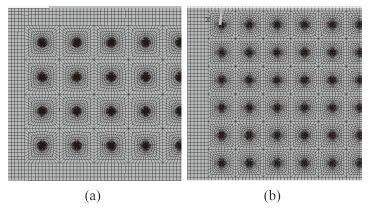
3.1 腐蚀坑数目对极限强度的影响点蚀密度(即平板表面的受蚀面积与原始面积的百分比)作为对结构腐蚀情况的重要评估参数,直观体现出了板格受腐蚀程度。为了研究蚀坑分布对板格极限强度的影响,本文选取了 4*9 和 6*11 两种腐蚀分布情况。仍然取深度为原板厚的一半,蚀坑直径为30 mm。即 DOP 分别等于 5.08%,9.33%。如图 4 所示。
|
图 4 腐蚀板 1/2 模型 Fig. 4 1/2 model of corrosion plate |
2 种腐蚀情况下的极限强度分别为 117.49 MPa,114.8 MPa,图 4(a) 中腐蚀面积比图 4(b)小了约 83%,然而强度差异甚小。因此,仅单独地将腐蚀面积用于表征板的腐蚀程度还有所欠缺。为探讨基于腐蚀面积相同的情况下,究竟是蚀坑数目还是蚀坑直径作为极限强度的控制因素,现选取了如表 3 所示几种表面受蚀情况。
|
|
表 3 不同蚀坑数目的极限强度 Tab.3 Ultimate strength of different numbers of corrosion pits |
从表 3 中计算出结果发现,在表面腐蚀面积以及腐蚀体积相同情况下,蚀坑的分布决定了极限强度的大小。而蚀坑数目的分布直接影响的是横截面的大小不同。图 5(a)模型中横截面积损失小于图 5(b)模型。表明当表面腐蚀面积相同时,采用点蚀后的横截面描述极限强度可行,这与文献[8]的研究结论一致。
3.2 蚀坑的几何参数对极限强度的影响为研究蚀坑深度以及直径对板格极限抗压强度的影响。取板格腐蚀模型为 4*9 模型,腐蚀坑圆柱直径为 26,30,36,40 mm。现分别取蚀坑深度为 0,0.25 t,0.5 t,0.75 t 四种情况,就以上几种情况运用 Ansys 分析如下:
由表 4 中数值软件计算汇总结果可知,当板面内承受双向压缩载荷且面外有恒定的侧向载荷时,随着腐蚀坑深度的增加,极限承载能力是逐渐减小。现选取直径等于 30 mm 为例,当蚀坑深度小于 0.5 t 时,平板的极限强度损失率分别为 12.6% 和 7.9%。当板剩余厚度小于 0.5 t 时,纵向极限强度损失率为 2.1%。深度从 0.25 t 变化到 0.75 t,极限强度分别减小了 9.9% ,8.5%,12.3%,13.9%。图 6 所示为蚀坑直径等于 26 mm 时极限强度随蚀坑深度的变化趋势。当腐蚀深度等于 0.25 t 时,蚀坑直径 26~40 mm 下的极限强度由 130.78 MPa 变成了 120.86 MPa,极限压缩强度损失率为 7.5%,而相应的其他厚度引起的损失率分别为 11.6% 和 12.9%。通过计算每种情况的体积损失率是 1.9%,2.5%,3.7%,4.5% 和 1.3%,2.6%,3.9%可以发现,强度的折减与腐蚀体积成正相关,与现有文献中的结论一致。同时,1/2 板厚是蚀坑深度对整个板强度的分界点,当蚀坑深度在 0~0.5 t 与在 0.5 t~1 t 之间变化时,极限强度对前者的变化更加敏感。因腐蚀直径的不同造成的极限强度差异很小。
|
|
表 4 不同几何参数的极限强度 Tab.4 Ultimate strength of different geometric parameters |
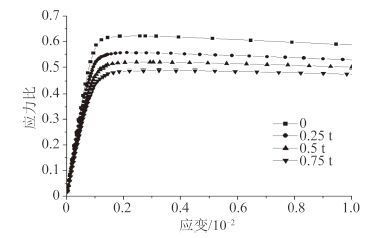
|
图 5 蚀坑深度变化的影响 Fig. 5 Influence of depth of corrosion pits |
通过对含腐蚀板进行非线性分析可得到如下结论:
1)在对船底板结构进行强度计算时,是否计及侧向载荷对整个板的极限承载能力有很大的影响,尤其当双轴受压的情况。在各种计算工况下,极限强度峰值也是有明显的差异。
2)在同等腐蚀面积下,蚀坑分布的不同能够在一定程度上影响板的极限承载能力。横截面积的损失是导致强度变化的主要因素。
3)单就蚀坑直径与深度的变化而言,深度对强度的影响更大,并且当深度在小于 1/2 板厚之间变化时,相对应的极限强度折减较大于 1/2 板厚更明显。腐蚀体积是影响极限强度的关键因素。
| [1] | PAIK J K, THAYAMBALLI A K. Ultimate strength of ageing ships[J]. Engineering for Maritime Environment , 2002, 216 (M1) :57–77. |
| [2] | PAIK J K, LEE J M, KO M J. Ultimate shear strength of plate elements with pit corrosion wastage[J]. Thin-Walled Structures , 2004, 42 :1161–1176. DOI: 10.1016/j.tws.2004.03.024 |
| [3] | NAKAI T. Effect of corrosion on static strength of hull structural members(1st report)[J]. J Soc Naval Arch Jpn , 2002, 192 :357–365. |
| [4] | DUNBAR T E, PEGG N, TAHERI F. A computational investigation of the effects of localized corrosion on plates and stiffened panels[J]. Marine Structures , 2004, 17 :385–402. DOI: 10.1016/j.marstruc.2004.08.012 |
| [5] | 王燕舞. 考虑腐蚀影响船舶结构极限强度研究[D]. 上海: 上海交通大学. 2008. |
| [6] | 江晓俐, 吴卫国, 梁志勇. 点腐蚀作用下非穿透低碳钢板的极限抗压承载能力数值分析[J]. 武汉理工大学学报(交通科学与工程版) , 2009, 33 :1167–1170. |
| [7] | 张岩, 黄一, 刘刚. 点蚀损伤船体结构板的极限剪切屈曲强度研究[J]. 船舶力学, 2013, 17(1-2): 102-110. |
| [8] | PAIK J K, WANG G, Thayamballi AK, et al. (2003b). Time-dependent risk assessment of aging ships accounting for general/pit corrosion, fatigue cracking and local denting. SNAME Trans;111. |
 2017, Vol. 39
2017, Vol. 39
