2. 高新船舶与深海开发装备协同创新中心,上海 200240;
3. 中国船级社规范与技术中心,上海 200135
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China;
3. Rules & Technology Center, China Classification Society, Shanghai 200135, China
载人深潜器可直接携带科考人员进入深海,在生物研究、地质考察、海底失物搜寻等方面发挥着重要作用。耐压球壳作为载人深潜器的关键部件直接关系到人员安全和设备使用,载人深潜器在服役期间一般根据具体的科考需求赴不同深度的海域执行任务,其每次下潜可视为一个载荷循环,近年来耐压球壳的疲劳问题引起了一些学者的重视[1-2],但相关研究并没有充分考虑焊接残余应力的影响。一般情况下,拉伸残余应力的存在能明显降低焊接结构的疲劳寿命,忽略拉伸残余应力的影响将使疲劳寿命评估结果偏于危险。耐压球壳开口结构通过焊接形式与壳体相连,开口焊趾处不可避免由于焊接材料的不均匀收缩或焊接装配时结构变形的约束作用而产生拉伸残余应力,疲劳寿命预报时其影响不可忽略。
潜器的疲劳寿命一般可分为工艺疲劳寿命和使用疲劳寿命。耐压球壳多采用高强度材料,属中厚球壳结构,且局部应力水平相对较高,有别于一般的船体薄壁构件。本文考虑焊趾处残余应力的影响,分别采用局部应力-应变法和裂纹扩展理论预报耐压球壳的工艺疲劳寿命和使用疲劳寿命,并研究焊接残余应力大小对疲劳寿命的影响。
1 焊接残余应力分布及疲劳评估位置本文研究载人深潜器设计下潜深度 7 000 m,耐压球壳采用高强度钛合金材料,共有 4 个开孔,其中人员出入孔位于球壳顶部,球壳前侧分布 1 个主观察窗和 2 个副观察窗,如图 1 所示。

|
图 1 耐压球壳最大主应变分布 Fig. 1 Max principal strain fringe of spherical shell |
潜艇和深潜器耐压球壳皆采用高强度材料,两者结构及载荷环境具有诸多相似之处,本文耐压球壳焊趾表面拉伸残余应力的大小参考潜艇残余应力的相关研究成果选取。
对于垂直于焊缝的横向残余应力问题,石德新等[3]以高强钢潜艇锥柱结合结构为研究对象,分析了焊接残余应力的大小,结果表明焊趾表面横向残余应力为拉应力,按危险的情况可取最大值约为 0.3σs,σs 为材料的屈服极限;吴雪珍[4]采用模拟分段开展了潜艇结构残余应力研究,模型较大且采用 VHD402 高强度钢厚板,与实艇的残余应力值较为接近,实测得到的凸锥处垂直于焊缝方向的残余应力基本相对焊缝中心对称分布,在焊缝附近残余拉应力达到最大值,约为 0.3σs。
耐压球壳的焊接采用多道焊形式,为研究此类结构焊接残余应力的分布形式,Ikushima 等[5]测量了77 mm 多道焊厚管结构(X 型沟槽,23 层,108 道)轴向残余应力沿壁厚方向的分布,研究表明垂直于焊缝方向的残余应力在外表面表现为拉伸应力,沿厚度方向拉伸残余应力逐渐降低并出现压缩残余应力,在约 1/2 厚度处压缩残余应力达到最大值。因此若板厚为t,则残余应力σR 沿壁厚分布形式可简化为以下线性分布形式(焊趾表面x = 0,内侧x =t)为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _R}(x) = {\sigma _R}(1- 4x/t),\left( {0 \leqslant x \leqslant t/2} \right),}\\ {{\sigma _R}(x) = {\sigma _R}(4x/t- 3),\left( {t/2 \leqslant x \leqslant t} \right)。} \end{array}{\rm{ }}} \right. $ | (1) |
参考上述残余应力分布规律的研究结论,本文计算耐压球壳工艺疲劳寿命及使用疲劳寿命时,均假定垂直于焊缝方向的残余应力沿壁厚具有线性分布的形式,在焊趾表面拉应力达到最大值 0.3σs ,沿厚度方向残余应力线性递减并在 1/2 厚度处出现最大压缩残余应力,大小为 0.3σs ,残余应力关于球壳的中面对称分布。
为确定耐压球壳疲劳评估位置,采用有限元软件计算耐压球壳在极限下潜深度(即下潜深度为 7 000 m)时的应变响应。计算模型采用精度较高的 20 节点 6 面体单元,开口焊趾和观察窗内侧等局部结构单元尺寸约为耐压球壳厚度的一半,沿球壳厚度方向分为 2 层。球壳受外部水压力作用,采用三点约束来消除刚体位移。耐压球壳最大主应变分布如图 1 所示。从图 1中可看出,在外部水压力载荷作用下,耐压球壳应变较大的位置出现在人员出入孔、主观察窗、副观察窗内侧及开口焊趾表面处,其中主、副观察窗由于距离较近,开口间相互影响使得 2 个观察窗开口焊趾表面应变分布不均,局部应变较大,球壳其余部分应变较小且分布均匀。耐压球壳最大主应变出现在人员出入孔内侧,此处较易发生疲劳破坏。由于球壳表面各开口焊趾处应变水平较高,同时焊趾处容易受拉伸焊接残余应力的影响而降低疲劳寿命,所以分别对耐压球壳人员出入孔内侧以及人员出入孔、主观察窗、副观察窗开口焊趾处应变最大位置进行疲劳寿命分析。各评估位置处的最大主应变见表 1。
|
|
表 1 耐压球壳各疲劳评估位置最大主应变 Tab.1 Max principal strain value of different fatigue calculation positions |
耐压球壳工艺疲劳寿命预报采用局部应力-应变法。局部应力-应变法的基本假设为:若结构缺口根部的局部应力-应变历史与光滑试样的应力-应变历史相同,则两者具有相同的疲劳寿命。本文采用工程上常用的 Neuber 近似法计算结构的局部应力-应变响应,结合材料循环应力-应变曲线,Neuber 近似法计算结构局部应力-应变响应可等效成求解以下方程组:
| $ \left\{ {\begin{array}{*{20}{l}} {\Delta \sigma \cdot \Delta \varepsilon = \frac{{{{\left( {{K_f}\Delta S} \right)}^2}}}{E},}\\ {\frac{{\Delta \varepsilon }}{2} = \frac{{\Delta {\varepsilon _e}}}{2} + \frac{{\Delta {\varepsilon _p}}}{2} = \frac{{\Delta \sigma }}{{2E}} + {{\left( {\frac{{\Delta \sigma }}{{2{K'}}}} \right)}^{\frac{1}{{{n'}}}}}。} \end{array}} \right. $ | (2) |
式中:∆σ 为局部应力范围;∆ε 为局部应变范围;Kf 为有效应力集中系数;∆S 为名义应力范围;E 为弹性模量;∆εe 为应变范围的弹性分量;∆εp 为应变范围的塑性分量;K1 为循环强度系数;n1 为循环应变硬化指数。
反映材料低周疲劳特性的ε-N 曲线采用 Coffin-Manson-Basquin 方程。当材料处于弹性范围时,平均应力σm 对疲劳寿命的影响不可忽略,而塑性变形起主导作用的情况下,由于平均应力的松弛效应,其影响将大大减弱,所以通常只对ε-N 曲线的弹性部分进行平均应力修正,采用的修正方法是 Morrow 根据 Goodman 公式推导出的平均应力修正公式,修正后的ε-N 曲线形式如下:
| $ \frac{{\Delta \varepsilon }}{2} = \frac{{\Delta {\varepsilon _e}}}{2} + \frac{{\Delta {\varepsilon _p}}}{2} = \frac{{\sigma _f'- {\sigma _m}}}{E}{\left( {2{N_f}} \right)^b} + \varepsilon _f'{\left( {2{N_f}} \right)^c}。 $ | (3) |
式中:σ’f 为疲劳强度系数;b 为疲劳强度指数;ε’f 为疲劳延性系数;c 为疲劳延性指数;Nf 为循环计数的疲劳寿命。结合 Coffin-Manson-Basquin 应变-寿命曲线,分别采用弹性应变幅εe 和塑性应变幅εp 为疲劳损伤参量,计算每个循环载荷引起的疲劳损伤,疲劳总损伤度和疲劳寿命根据 Miner 累积损伤准则确定。
耐压球壳工艺疲劳寿命计算时,焊接残余应力的影响通过平均应力修正来体现,即认为耐压球壳表面开口焊趾处拉伸残余应力的存在提高了平均应力水平,而没有改变焊趾处的局部应变幅。计算时为充分考虑应力集中和材料焊接缺陷等不利因素,有效应力集中系数取Kf = 2,其余参数见表 2。
|
|
表 2 钛合金材料参数 Tab.2 Material parameter of titanium alloy |
考虑载人深潜器极限下潜工况,即每次下潜至 7 000 m 再返回水面为一个载荷循环。耐压球壳的工艺疲劳寿命预报结果如表 3 所示。
|
|
表 3 耐压球壳工艺疲劳寿命预报结果(单位:次) Tab.3 Prediction results of spherical shell crack initiation fatigue life(Unit:cycle) |
耐压球壳设计下潜次数为 4 000 次,从表中可看出:各疲劳评估位置的工艺疲劳寿命均大于耐压球壳的设计寿命,具有较高的安全裕度;不考虑焊趾表面拉伸残余应力的影响时,工艺疲劳寿命最小值出现在人员出入孔内侧,为 155 005 次,这是因为每次极限下潜循环过程中,人员出入孔内侧的应变范围最大,因此最容易发生疲劳破坏;考虑焊趾表面拉伸残余应力影响后,各评估位置的工艺疲劳寿命平均降幅为 76%,此时工艺疲劳寿命最小值出现在副观察窗表面焊趾处,为 107 239 次,并且小于人员出入孔内侧的工艺疲劳寿命。
以上分析结果表明,焊趾表面拉伸残余应力的存在将降低耐压球壳的工艺疲劳寿命,忽略焊趾处拉伸残余应力的影响将导致工艺疲劳寿命预测结果偏于危险,并且实际疲劳破坏的位置可能与预测结果出现偏差,因此在耐压球壳工艺疲劳寿命预报中有必要计入焊接残余应力的影响。
2.2 耐压球壳使用疲劳寿命焊接结构不可避免存在焊接缺陷,耐压球壳开口焊趾在循环载荷作用下也同样会萌生裂纹。本文考虑焊接残余应力的影响,采用裂纹扩展理论预报含初始缺陷耐压球壳的使用疲劳寿命。根据耐压球壳整体受压的特点,使用疲劳寿命计算采用裂纹扩展单一曲线模型[6-7]。该模型能计及负应力比R 的影响,同时形式简洁,可以将不同应力比下的裂纹扩展曲线压缩到R = 0 对应的曲线附近,从而只需知道R = 0 所对应的材料参数即可对承受随机载荷的结构进行使用疲劳寿命预测,在工程使用中具有重要意义。计算公式如下:
| $ \frac{{{\rm{d}}a}}{{{\rm{d}}N}} = C\left( {\Delta {K_E}^m- \Delta {K_{th}}^m} \right), $ | (4) |
| $ \Delta {K_E} = M\Delta K, $ | (5) |
| $ M = \left\{ {\begin{array}{*{20}{l}} {{{\left( {1- R} \right)}^{- {\beta _1}},}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {R < 0} \right),}\\ {{{\left( {1- R} \right)}^{- \beta },}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {0 \leqslant R < 0.5} \right),}\\ {{{(1.05- 1.4R + 0.6{R^2})}^{- \beta },}\;\;\;\;\;\left( {0.5 \leqslant R < 1} \right)。} \end{array}} \right. $ | (6) |
式中:C 和m 为材料系数,与R = 0 时对应的 Paris 公式材料系数相同;∆KE 和 ∆Kth 为相当于应力比R = 0 时的等效应力强度因子幅和应力强度因子幅门槛值;β 和β1 为材料参数。
耐压球壳开口焊趾裂纹形式采用工程实际中最常见的半椭圆表面裂纹,本文基于有限元分析手段,采用张开位移法计算外部水压力和焊接残余应力联合作用下开口焊趾处表面裂纹的应力强度因子。根据文献[8]的建议,围绕裂纹尖端采用 20 节点奇异元,该单元稳定可靠且满足精度要求,网格划分时,裂纹尖端单元角度α = 45°,围绕裂纹尖端单元层数n = 3。
载人深潜器下潜时,耐压球壳整体受压,目前一般认为压-压循环载荷作用下裂纹扩展至某一尺寸即发生休眠。球壳开口焊趾处拉伸残余应力的存在,使得该局部区域在下潜过程中承受拉-压循环载荷,此时拉伸残余应力将降低耐压球壳的使用疲劳寿命,其影响不可忽略。偏于保守起见,本文假定深潜器每次均下潜至最大深度 7 000 m,同时暂不考虑门槛值效应。计算参数根据工程试验及相关文献[6]选取(见表 4)。
|
|
表 4 耐压球壳使用疲劳寿命计算参数 Tab.4 Parameter for calculating crack propagation life |
计算结果显示人员出入孔、主观察窗和副观察窗焊趾处的使用疲劳寿命分别为 33 589 次、80 302 次和 30 919 次,均显著高于该球壳的设计寿命,具有较高的安全裕度。每次极限下潜时,由于副观察窗焊趾处局部应力高于人员出入孔和主观察窗,所承受的交变应力幅值最大,因此相应的使用疲劳寿命最低。
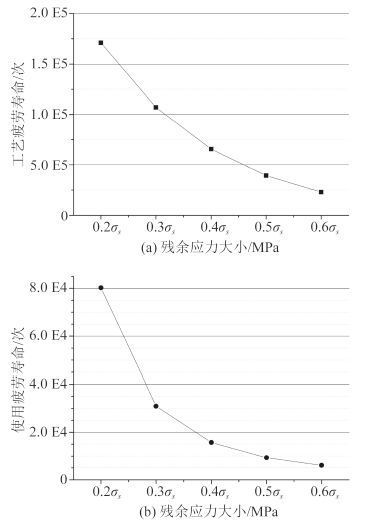
3 焊接残余应力大小的影响影响焊接残余应力的因素包括材料性能、不同类型焊接热源、焊接结构刚性、焊接结构尺寸和焊接工艺顺序等,准确地预测焊接残余应力十分困难。本文所研究耐压球壳实际焊接残余应力大小与潜艇结构可能存在差异,因此有必要计算焊趾处拉伸残余应力大小在一定范围内变化对耐压球壳疲劳寿命的影响。根据本文耐压球壳工艺疲劳寿命和使用疲劳寿命计算结果可知,该球壳副观察窗表面焊趾处最易疲劳破坏,现选取该位置计算拉伸残余应力在(0.2~0.6)σs 范围内变化对耐压球壳疲劳寿命的影响,计算结果如图 2 所示。
|
图 2 焊接残余应力大小的影响 Fig. 2 The influence of welding residual stress |
从图 2 中可看出,耐压球壳的工艺疲劳寿命和使用疲劳寿命均随焊接残余应力的提高而降低,当拉伸残余应力最大值取 0.6σs 时,球壳工艺疲劳寿命和使用疲劳寿命分别为 22 864 次和 6 058 次,仍高于设计寿命;拉伸残余应力每增加 0.1σs ,球壳工艺疲劳寿命降低约 40%,使用疲劳寿命降幅在 30%~60% 之间,因此降低拉伸焊接残余应力可以有效提高耐压球壳的疲劳寿命。
4 结语本文考虑耐压球壳开口焊趾处拉伸残余应力的影响,分别基于局部应力-应变法和能计及负应力比影响且形式简洁的单一曲线模型计算了某 7 000 m级载人深潜器耐压球壳的工艺疲劳寿命及使用疲劳寿命,并研究了焊接残余应力大小对疲劳寿命的影响,得到以下结论:
1)耐压球壳工艺疲劳寿命和使用疲劳寿命均大于球壳设计寿命,具有较高的安全裕度;
2)忽略开口焊趾处拉伸残余应力的影响将导致球壳工艺疲劳寿命预测结果偏于危险,并且实际疲劳破坏位置可能与预测结果出现偏差;
3)开口焊趾处拉伸残余应力使得整体受压的耐压球壳局部区域在下潜过程中承受拉-压循环载荷,降低耐压球壳的使用疲劳寿命,其影响不可忽略;
4)耐压球壳的工艺疲劳寿命和使用疲劳寿命均随焊接残余应力的提高而降低,降低拉伸焊接残余应力可以有效提高耐压球壳的疲劳寿命。
| [1] |
李向阳, 崔维成, 张文明. 钛合金载人球壳的疲劳寿命可靠性分析[J]. 船舶力学 , 2006, 10 (2):82–86.
LI Xiang-yang, CUI Wei-cheng, ZHANG Wen-ming. Fatigue life reliability analysis of Titanium manned spherical shell[J]. Journal of Ship Mechanics , 2006, 10 (2) :82–86. |
| [2] |
李良碧, 罗广恩, 王自力. 大深度载人潜水器疲劳寿命有限元分析[J]. 江苏科技大学学报(自然科学版) , 2006, 20 (3):1–5.
LI Liang-bi, LUO Guang-en, WANG Zi-li. Fatigue Life Analysis of Deep Manned Submersible by Using Finite Element Method[J]. Journal of Jiangsu University of Science and Technology(Natural Science Edition) , 2006, 20 (3) :1–5. |
| [3] |
石德新, 耿峰, 黄小平, 等. 潜艇结构疲劳裂纹形成寿命分析[J]. 哈尔滨工程大学学报 , 2000, 21 (3):70–74.
SHI De-xin, GENG Feng, HUANG Xiao-ping, et al. Analysis of Fatigue Crack Initiation Life of Submarine Structure[J]. Journal of Harbin Engineering University , 2000, 21 (3) :70–74. |
| [4] | 吴雪珍. VHD402钢中间试验模拟分段的残余应力研究[J]. 舰船科学技术 , 1992, 14 (1):1–11. |
| [5] | IKUSHIMA K, SHIBAHARA M. Large-scale non-linear analysis of residual stresses in multi-pass pipe welds by idealized explicit FEM[J]. Weld World , 2015, 59 (6) :839–850. DOI: 10.1007/s40194-015-0263-y |
| [6] | HUANG X, MOAN T. Improved modeling of the effect of R-ratio on crack growth rate[J]. International Journal of Fatigue , 2007, 29 (4) :591–602. DOI: 10.1016/j.ijfatigue.2006.07.014 |
| [7] | HUANG X, MOAN T, CUI W. A unique crack growth rate curve method for fatigue life prediction of steel structures[J]. Ships and Offshore Structures , 2009, 4 (2) :165–173. DOI: 10.1080/17445300902732370 |
| [8] |
陈景杰, 黄一, 刘刚. 基于奇异元计算分析裂纹尖端应力强度因子[J]. 中国造船 , 2010, 51 (3):56–64.
CHEN Jing-jie, HUANG Yi, LIU Gang. Analysis of Finite Element Model for Calculating Stress Intensity Factor Based on Crack-tip Singular Element[J]. Shipbuilding of China , 2010, 51 (3) :56–64. |
 2017, Vol. 39
2017, Vol. 39
