海军工程大学 舰船工程系,湖北 武汉 430033
收稿日期: 2016-04-13, 修回日期: 2016-05-17.
作者简介: 吴兴亚(1992-),男,硕士研究生,研究方向为舰船流体动力性能。
Research on calculation method of hydrodynamic derivatives based on maneuvering equation
Department of Naval Architecture Engineering, Naval University of Engineering, Wuhan 430033, China
0 引言 船舶操纵性作为船舶性能研究的重点,始终是影响船舶安全航行的重要因素之一。目前,通常有基于特征参数的回归公式或数据库的方法、自由自航模试验方法及基于数学模型的数值计算这 3 种基本方法预报船舶的操纵性。其中,基于数学模型的数值计算,即利用船舶操纵运动方程加上计算机模拟计算是最为普遍的方法,而此方法的核心就是求解船舶操纵运动方程中的水动力导数。
目前水动力导数的确定方法通常包括约束模型试验法、自航模型试验加系统辨识法、数据库或回归公式估算法以及数值计算法。约束模型试验法由于其试验花费较高且周期较长,同时船模与实船之间存在着尺度效应,使其实用性受到限制;自航模型试验加系统辨识法近年来得到不断地开发与应用,目前出现诸如神经网络、最小二乘、卡尔曼滤波等系统辨识法应用于预报水动力导数。文献 [1-2] 分别基于 RBF 网络和 BP 神经网络对船舶操纵水动力导数进行了计算研究,Abkowitz 基于卡尔曼滤波(extended kalman filter,EKF)辨识法,将其运用到 Esso Osaka 油轮的操纵试验分析结果,得到了较为理想的系统辨识结果。近年来,相关学者建立起系列数据库能对船舶设计初始阶段的水动力导数进行估算[3-7],其局限性在于对于新船型无法进行相应估算;而随着计算机科学技术的飞速发展以及计算流体力学(CFD)技术对船舶水动力性能的准确预报,通过对商用流体力学软件二次开发成为计算水动力导数的有效方法,文献 [8] 借助 fluent 的二次开发对相关水动力导数进行了计算。
1 数值计算方法 1.1 控制方程 在用数值模拟船体周围流场时,认为水为不可压缩的粘性流体且在流场流动时遵循质量守恒定律及动量守恒定律,其张量形式下的连续性方程和雷诺平均 Navier-stokes(Reynolds-Averaged Navier-stokes,RANS)方程如下:
|
$ \frac{{\partial {{\bar u}_i}}}{{\partial {x_i}}} = 0 , $
|
(1) |
|
$ \begin{array}{l} {\rm{\rho }}\frac{{\partial {{\bar u}_i}}}{{\partial t}} + \rho {{\bar u}_j}\frac{{\partial {u_i}}}{{\partial {x_j}}} =- \frac{{\partial {{\bar p}_i}}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left( {\mu \frac{{\partial {{\bar u}_i}}}{{\partial {x_j}}}- \rho \overline {u_i'u_j'} } \right) \end{array}。 $
|
(2) |
式中:ui
为流体平均速度分量;P 为平均压力;ρ 为流体质量密度;μ 为流体动力粘性系数。
1.2 湍流模型 当前在工程中广泛使用的是标准k-ε 模型、Realizablek-ε 模型和标准k-ω 模型等。综合考虑各模型的适用条件范围,通常在求解分离和复杂二次流特征流动时,采用 Realizablek-ε 湍流模型进行 RANS 方程的封闭。Realizablek-ε 模型输运方程如下:
|
$ \begin{array}{l} {\rm{\rho }}\frac{{dk}}{{dt}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} + {G_b}- \rho \varepsilon- {Y_M} \end{array}, $
|
(3) |
|
$ \begin{array}{l} {\rm{\rho }}\frac{{d\varepsilon }}{{dt}} = \frac{\partial }{{\partial {x_i}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_i}}}} \right] + \rho {C_1}S\varepsilon- \\[5pt] \, \, \quad \quad \rho {C_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {v\varepsilon } }} + {C_{1\varepsilon }}\frac{\varepsilon }{k}{C_{3\varepsilon }}{G_b}。 \end{array} $
|
(4) |
式中:Gk
、Gb
为湍流产生项;YM
为湍流耗散项;σk
和σε
为普朗特数;C1 和C1ε 为常数。
1.3 VOF 算法及 STAR-CCM+ 的求解原理应用 VOF 是一个简单的多项流模型,通过 VOF 算法中 VOF 波的设定,在三维情况下,使船模适用于 6 自由度运动模型。VOF 算法是一种处理自由面的方法,其求解原理是根据各个时刻流体在网格单元体积的变动量与网格单元自身体积的比值函数F来构造、追踪自由面,确定自由面的形状和位置。当在某一时刻网格单元中比值函数F = 1 时,说明该时刻状态下该网格单元均被指定相的流体充满,当F = 0 时,说明该单元均被另一相流体充满。F 函数满足方程:
|
$ \frac{{\partial F}}{{\partial t}} + u\frac{{\partial F}}{{\partial x}} + v\frac{{\partial F}}{{\partial y}} + w\frac{{\partial F}}{{\partial z}} = 0。 $
|
(5) |
应用 STAR-CCM+ 软件计算船体在各种运动工况下的水动力是本文的中心工作。在该软件平台上,结合 Realizablek-ε 湍流模型,采用 VOF 算法,通过求解 Navier-stokes(Reynolds-Averaged Navier-stokes,RANS)方程,对船模在不同工况下的运动进行数值模拟,求得船模所受的力和力矩,并通过后期的数据拟合分析得到船舶的各水动力导数。
2 数值计算模型 2.1 计算对象 本文的计算对象是 1 艘缩尺比为 1:18 的民用打捞船的玻璃钢船模,计算船模模型如图 1 所示,船模的无量纲化主要参数见表 1。
表 1(Tab. 1)

表 1 船模无量纲化主要参数
Tab. 1 The main dimensionless parameter of model
| 名称 |
参数值 |
| 型宽B/L
|
0.14 |
| 型深D/L
|
0.06 |
| 方形系数CB
|
0.60 |
| 设计吃水T/L
|
0.04 |
| 设计排水量 Δ/(ρLBT)
|
0.55 |
| 设计水线长LWL
/L
|
0.89 |
|
表 1 船模无量纲化主要参数
Tab.1 The main dimensionless parameter of model
|
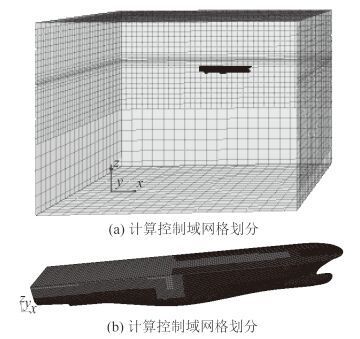
2.2 数值计算域 选取计算域如图 2 所示,在船体周围建立一个拖曳水池,选取船尾处水线面下 0.35 m 为坐标原点,在其上方 1.2L(L 为船长)处设定上界面,在其前方、后方各 2.4L 处分别设定入流界面和出流界面,在其左侧、右侧、下方 2.4L 处设定壁面。运用布尔运算使船体与拖曳水池分离,在船体表面设定无滑移壁面。
2.3 数值计算条件设定 由于船舶的实际操纵运动本质上是低频率运动,在求船舶操纵所需要的各水动力导数时,需要船舶作低频的振荡,故在拖曳水池中,船体自身不前进,使水流以规定流速流向船体,来满足计算状态。在设定边界条件时,入流界面设定为速度入口,出流界面设定为压力出口,各壁面均设定为无滑移边界条件。同时选用隐式不定常模式和欧拉多项流,利用 VOF 方法处理船体运动时兴波自由面重构等强非线性现象,湍流模式采用 K-Epsilon 模式。同时在 DFBI 中,根据船模具体的运动工况选取不同的运动模式以及自由度。
2.4 数值计算网格划分 计算控制域网格划分如图 3 所示。在对计算控制域进行网格划分时,为保证计算的可行性并节约计算时间,在对远离船模的周围控制域以及水线面以上船体的六面体网格进行划分时,采用稍微稀疏的网格,同时为保证计算结果的准确性,对水线面、球皮首等一些区域进行加密处理,保证计算中网格质量。
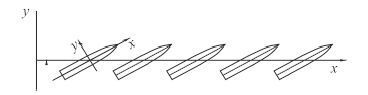
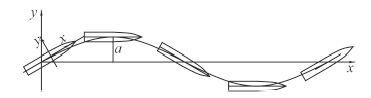
3 水动力导数计算模型及计算结果 3.1 斜行运动计算模型 船舶作斜航运动如图 4 所示。斜航运动中取系列船模漂角β 的值分别为 0°,± 0.5°,± 1°,± 2°,± 4° 和 ± 8°,该运动模式下船模的首摇角速度r = 0,航速V = 2.2 m/s,其运动方程为:
|
$ \nu =- V\sin \beta 。 $
|
(7) |
公式中:r 为船模角速度;ν 为侧向速度;V 为航速;β 为船模漂角。
计算不同漂角工况下船舶所受的水动力和力矩,包括船舶纵向方向所受水动力X,侧向所受水动力Y,船舶所受首摇力矩N 以及横倾力矩K。当漂角β 很小时,作用在坐标系上的速度分量可简化为:
|
$ \nu =- V\sin \beta \approx- V\beta 。 $
|
(8) |
由式(8)可知,通过改变船舶漂角值β,可得到一系列相应的船舶侧向速度v,从而可测得不同侧向速度下船舶所受侧向力以及首摇力矩,继而可以作出不同侧向速度下的侧向力曲线Y~v 及首摇力矩曲线N~v。由于船舶左右对称,其所受水动力方程可表达为:
|
$ {Y} = {Y_V}\nu + {Y_{VVV}}{\nu ^3}, $
|
(9) |
|
$ {N} = {N_V}\nu + {N_{VVV}}{\nu ^3}, $
|
(10) |
将通过计算所得的水动力、力矩以及侧向速度进行无因次化为:
|
$ Y' = \frac{Y}{{\frac{1}{2}\rho {V^2}{L^2}}}, $
|
(11) |
|
$ N' = \frac{N}{{\frac{1}{2}\rho {V^2}{L^3}}}, $
|
(12) |
|
$ \nu ' = \frac{\nu }{V} =- \sin \beta。 $
|
(13) |
最后将无因次水动力及力矩随无因次侧向速度的变化曲线通过 Matlab 进行拟合,分析拟合曲线方程即得到线性水动力导数Y′V
,N′V
及非线性水动力导数Y′VVV
和N′VVV
。
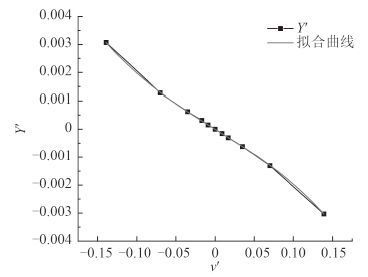
由图 5 可得不同侧向速度下侧向力曲线的拟合多项式方程为:
|
$ y\!=\!-2.89 \times {10^{\!-\!6}}\!-\!0.01736x\!+\!0.00101{x^2}\!-\!0.23733{x^3}, $
|
(14) |
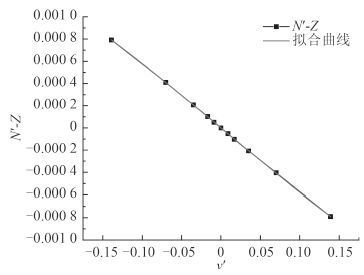
由图 6 可得不同侧向速度下首摇力矩曲线的拟合多项式方程为:
|
$ y\!=\!1.86\!\times\!{10^{\!-\!7}}\!-\!0.00589x\!+\!6.13205\!\times\!{10^{\!-\!5}}\!{x^2}\!+\!0.0104{x^3}。 $
|
(15) |
表 2(Tab. 2)

表 2 本文计算方法与回归公式法结果比较
Tab. 2 The result comparison with computation method presented and regression formula method
| 水动力导数 |
本文方法计算值 |
回归公式估算值 |
| Y′V
|
-0.017 36 |
-0.013 16 |
| N′V
|
-0.005 89 |
-0.004 79 |
|
表 2 本文计算方法与回归公式法结果比较
Tab.2 The result comparison with computation method presented and regression formula method
|
表 3(Tab. 3)

表 3 斜航运动非线性位置导数求解结果
Tab. 3 The result of nonlinear hydrodynamic derivatives with drifting motion
| 水动力导数 |
Y′VV
|
N′VV
|
Y′VVV
|
N′VVV
|
| 本文计算值(*103)
|
2.02 |
0.12 |
-1 423 |
62.4 |
|
表 3 斜航运动非线性位置导数求解结果
Tab.3 The result of nonlinear hydrodynamic derivatives with drifting motion
|
3.2 纯首摇运动计算模型 船舶作纯首摇运动如图 3 所示,在随船坐标系下,船舶侧向速度ν = 0,合速度方向与船舶中纵剖面方向一致,即在纯首摇运动中;纵向上,船舶作匀速运动;横向上,船舶作低频简谐振荡运动。与此同时,首向角也发生周期性的改变,其运动方程为:
|
$ \psi = {\psi _0}\cos \omega t, $
|
(16) |
|
$ {\psi _0} =- \frac{{a\omega }}{V}; $
|
(17) |
|
$ r = \dot \psi =- {\psi _0}\omega \sin \omega t, $
|
(18) |
|
$ \dot r = \ddot \psi =- {\psi _0}{\omega ^2}\cos \omega t。 $
|
(19) |
式中:Ψ 为首向角;Ψ0 为首向角幅值;a 为横向简谐振荡运动幅值;ω 为简谐运动频率;r 为角速度。
在纯首摇运动中,本文共设计 2 种计算方案:第 1 种方案为:振幅取固定值a = 0.15 m,首摇频率依次取 0.066 Hz,0.076 Hz,0.086 Hz,0.096 Hz 和 0.116 Hz 五种工况,分别计算每种工况下船舶所受的水动力;第 2 种方案为:首摇运动时简谐振荡频率取固定值ω = 0.066 Hz,振幅依次取 0.15 m,0.30 m,0.45 m,0.6 m 和 0.75 m 五种工况,分别计算每种工况下船舶所受的水动力。首摇运动时,船舶在随船坐标系下的水动力方程可表达为:
|
$ {Y} = {Y_r}r + {Y_{\dot r}}\dot r + {Y_{rrr}}{r^3}, $
|
(20) |
|
$ {N} = {N_r}r + {N_{\dot r}}\dot r + {N_{rrr}}{r^3}。 $
|
(21) |
将上述公式中的各参数进行无因次化并将首摇运动方程代入得到水动力表达式无量纲形式如下:
|
$ \begin{array}{l} Y' = Y_r'\left( {\frac{{a{\omega ^2}L}}{{{V^2}}}} \right)\sin \omega t + Y_{\dot r}'\left( {\frac{{a{\omega ^3}{L^2}}}{{{V^3}}}} \right)\cos \omega t + \\[5pt] \quad \quad Y_{rrr}'\frac{1}{6}{\left( {\frac{{a{\omega ^2}L}}{{{V^2}}}} \right)^3}{\left( {\sin \omega t} \right)^3}{\rm{ = }}\\[5pt] \quad \quad A\sin \omega t + B\cos \omega t + C{\left( {\sin \omega t} \right)^3}, \end{array} $
|
(22) |
|
$ \begin{array}{l} N' = N_r'\left( {\frac{{a{\omega ^2}L}}{{{V^2}}}} \right)\sin \omega t + N_{\dot r}'\left( {\frac{{a{\omega ^3}{L^2}}}{{{V^3}}}} \right)\cos \omega t + \\[5pt] N_{rrr}'\frac{1}{6}{\left( {\frac{{a{\omega ^2}L}}{{{V^2}}}} \right)^3}{\left( {\sin \omega t} \right)^3}{\rm{ = }} M\sin \omega t + N\cos \omega t + P{\left( {\sin \omega t} \right)^3}, \end{array} $
|
(23) |
其中:
|
$ {{A}} = Y_r'\left( {\frac{{a{\omega ^2}L}}{{{V^2}}}} \right), $
|
(24) |
|
$ {{B}} = Y_{\dot r}'\left( {\frac{{a{\omega ^3}{L^2}}}{{{V^3}}}} \right), $
|
(25) |
|
$ {{C}} = Y_{rrr}'\frac{1}{6}{\left( {\frac{{a{\omega ^2}L}}{{{V^2}}}} \right)^3}, $
|
(26) |
|
$ {{M}} = N_r'\left( {\frac{{a{\omega ^2}L}}{{{V^2}}}} \right), $
|
(27) |
|
$ {{N}} = N_{\dot r}'\left( {\frac{{a{\omega ^3}{L^2}}}{{{V^3}}}} \right), $
|
(28) |
|
$ {{P}} = N_{rrr}'\frac{1}{6}{\left( {\frac{{a{\omega ^2}L}}{{{V^2}}}} \right)^3}。 $
|
(29) |
由上述无量纲化水动力表达方程可知,将船舶在首摇运动中所受的水动力曲线运用 Maylab 进行拟合,得到方程中的各系数项A,B,C,M,N,P,由各系数的方程表达式可知,通过方案 1 的固定幅值a 取不同的振荡频率ω 和方案 2 的固定频率ω 取不同的幅值a 进行二次曲线拟合,均可以求得各水动力导数。通过 2 种方案互相验证并与由经验公式所得数值进行比对,可探求运用 STAR-CCM+ 求取该类水动力导数的准确性。
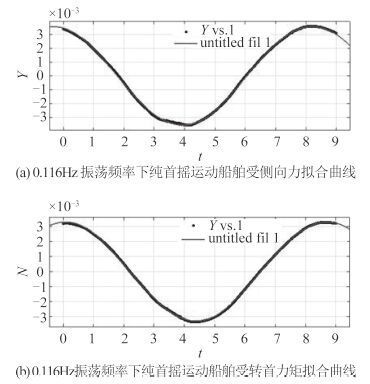
3.2.1 方案 1(固定幅值取不同首摇频率)下计算结果 图 8 为选取振幅a = 0.15 m,船舶摇首频率为 0.116 Hz工况下的船舶受力曲线,2 条曲线分别在各自受力稳定周期内,保证了船体受力的稳定性。并通过 Matlab 进行曲线拟合,得到船舶受力的曲线方程。
拟合曲线方程分别为:
|
$ \begin{split} \\[-12pt] y =& 0.0008424\sin \omega t + 0.003464\cos \omega t + \\ & 0.0001224{\left( {\sin \omega t} \right)^3}; \end{split} $
|
(30) |
|
$ \begin{split} \\[-12pt] y =& 0.00065\sin \omega t + 0.003279\cos \omega t + \\& 0.000103{\left( {\sin \omega t} \right)^3}。 \end{split} $
|
(31) |
由上述 5 种工况下的拟合曲线可求得无量纲水动力表达式方程中的各系数项,进而利用 Matlab 对所得数据结果进行二次拟合,最后求得船舶纯首摇状态下的各水动力导数。
表 4(Tab. 4)

表 4 本文计算方法与回归公式法结果比较
Tab. 4 The result comparison with computation method presented and regression formula method
| 水动力导数 |
本文方法计算值 |
回归公式估算值 |
| Y′r
|
0.003 23 |
0.003 154 |
| N′r
|
-0.002 41 |
-0.002 21 |
|
表 4 本文计算方法与回归公式法结果比较
Tab.4 The result comparison with computation method presented and regression formula method
|
表 5(Tab. 5)

表 5 纯首摇运动非线性水动力导数求解结果
Tab. 5 The result of nonlinear hydrodynamic derivatives with yawing motion
| 水动力导数 |
$Y_{\dot r}'$
| |
$N_{\dot r}'$
|
Y′rrr
|
N′rrr
|
| 本文计算值(*103)
|
8.92 | |
9.43 |
58.9 |
-299.7 |
|
表 5 纯首摇运动非线性水动力导数求解结果
Tab.5 The result of nonlinear hydrodynamic derivatives with yawing motion
|
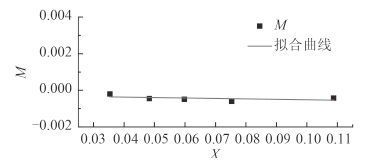
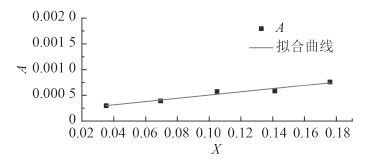
3.2.2 方案 2 (固定频率取不同振荡幅值)下计算结果 由上述 5 种不同振荡幅值工况下的拟合曲线可求得无量纲水动力表达式方程中的各系数项,进而利用 Matlab对所得数据结果进行二次拟合,见图 11~图 12,最后求得不同振动幅值下船舶纯首摇状态下的各水动力导数。
表 6(Tab. 6)

表 6 本文计算方法与回归公式法结果比较
Tab. 6 The result comparison with computation method presented and regression formula method
| 水动力导数 |
本文方法计算值 |
回归公式估算值 |
| Y′r
|
0.003 16 |
0.003 154 |
| N′r
|
-0.002 87 |
-0.002 21 |
|
表 6 本文计算方法与回归公式法结果比较
Tab.6 The result comparison with computation method presented and regression formula method
|
4 结语 在 STAR-CCM+ 软件平台基础上,本文针对某一具体船模,通过求解 RANS 方程,采用多相流 VOF 算法,数值计算了该船模按固定漂角斜航、纯横荡及 2 种振荡模式下的纯首摇 3 种工况下的 PMM 运动水动力导数,结果表明:
1) 通过该方法数值计算所得的线性水动力导数与采用回归公式计算结果在较小误差范围内,两者吻合度较好,证实了基于 STAR-CCM+ 软件平台采用 PMM 运动数值模拟计算线性水动力导数的可靠性与准确性。
2)采用固定幅值下不同振荡频率与固定频率下不同幅值两种纯首摇运动工况求取水动力导数,两者计算结果相吻合,进一步证实了本文方法计算船舶特定水动力导数的真实性。
3)基于本文方法对船舶水动力导数的可靠求解,为下一步的船舶操纵性仿真预报的开展奠定了基础。



 2017, Vol. 39
2017, Vol. 39
