0 引言

潜艇有单壳体和双壳体 2 种结构形式，不同的结构形式引起的振动声辐射明显不同，一直以来，国内外不少学者对单壳体和双壳体水下结构的振动声辐射问题开展了广泛研究。祁立波等^[1] 揭示了不同激励力下水下加肋圆柱壳体低频声辐射特征。夏齐强等^[2] 从控制内壳振动和衰减壳间振动传递的角度对双层圆柱壳体进行了结构声学设计。针对单/双层水下结构的振动声辐射对比分析问题，金广文等^[3] 研究了壳体长度、壳体厚度、有无环肋以及环肋间距不同参数下单/双层圆柱壳体结构的振动均方加速度级，但并没有考虑壳体的声辐射问题。唐俊娟等^[4] 和李兵等^[5] 研究了不同激励方式下的单/双层舱段圆柱壳体的振动声辐射问题，但并未对螺旋桨激励下的振动声辐射问题加以研究

对于复杂水下结构的振动声辐射问题，解析法求解很难实现。吴有生^[6] 将三维适航理论与结构力学理论相结合，在考虑水为不可压缩介质的情况下，提出了三维水弹性力学理论。邹明松^[7] 等在三维水弹性力学理论基础上研究了水下弹性体结构近场点声压和远场声辐射的计算方法，同时对计算方法的有效性进行了验证，并在 Abaqus 软件的基础上二次开发了三维水弹性声学分析软件 Thafts-acoustic。

1 三维声弹性力学理论

由模态叠加法，船体结构离散系统的节点位移可表示为：

${u} = \sum\limits_{r = 1}^m {{{u}_r}{q_r}} = \sum\limits_{r = 1}^m {\left\{ {{u_r},{v_r},{w_r}} \right\}{q_r}},$

(1)

式中 ${q_r}\left( {r = 1,2, \cdots ,m} \right)$ 为第r 阶干模态的主坐标分量。

假设弹性船体周围水为均匀可压、无粘的理想声介质，只考虑船舶航行诱导的扰动流场以及由结构振动诱导的声波场都是微幅线性的，总的流场速度势可表示为各阶声波辐射速度势的线性叠加：

$\Phi \left( {x,y,z,t} \right) = \sum\limits_{r = 1}^m {{\phi _r}\left( {x,y,z,t} \right)} ,$

(2)

式中 $\left( {x,y,z} \right)$ 为场点的坐标。

声波速度势 $\phi $ 满足 Helmholtz 方程为：

${\nabla ^2}\phi- \frac{{{\partial ^2}\phi }}{{\partial {t^2}}} = 0,$

(3)

船体流固湿表面边界条件为：

$\frac{{\partial {\phi _r}}}{{\partial {{n}}}} = iw\left( {{u_r}{n_1} + {v_r}{n_2} + {w_r}{n_3}} \right)。$

(4)

式中： ${u_r},{v_r},{w_r}$ 为第r 阶干模态位移； n 为流固湿表面单位法向量。

与自由液面边界条件对应的 Green 函数为：

$G\left( {P,Q} \right) = \frac{1}{{4\pi {r_1}}}{e^{- ik{r_1}}}- \frac{1}{{4\pi {r_2}}}{e^{- ik{r_2}}}。$

(5)

式中: ${r_1} = \sqrt {{{\left( {x- \xi } \right)}^2} + {{\left( {y- \eta } \right)}^2} + {{\left( {z- \zeta } \right)}^2}} $ ； ${r_2} = \sqrt {{{\left( {x- \xi } \right)}^2} + {{\left( {y- \eta } \right)}^2} + {{\left( {z + \zeta } \right)}^2}} $ ； $k = \omega /{c_0}$ 为流体中声波波数； $\left( {x,y,z} \right)$ 为场点P 的坐标； $\left( {\xi ,\eta ,\zeta } \right)$ 为源点Q 的坐标。

针对各阶干模态可得到对应的简单源边界积分方程：

$\phi \left( P \right) = \frac{1}{{4\pi }}\int \!\!{\int_{\bar S} {\sigma \left( Q \right)G\left( {P,Q} \right){\rm{d}}{S_Q}} } ,$

(6)

频域内的船舶声弹耦合动力学方程为：

$\left[ {a + A} \right]\left\{ {\ddot q} \right\} + \left[ {b + B} \right]\left\{ {\dot q} \right\} + \left[ {c + C} \right]\left\{ q \right\} = \left\{ \Xi \right\}$

(7)

式中： $\left\{ q \right\}$ 为广义位移向量； $\left\{ \Xi \right\}$ 为广义力向量；[a]，[b]，[c] 为干结构广义质量、阻尼和刚度矩阵；[A]，[B]，[C] 为广义流体附加质量、附加阻尼和恢复力系数矩阵。其表达式为：

$\left. {\begin{array}{*{20}{l}} {{A_{rk}}}\\ {{B_{rk}}} \end{array}} \right\} = \left. {\begin{array}{*{20}{l}} {\frac{1}{{{\omega ^2}}}{\rm{Re}}}\\ {- \frac{1}{\omega }{\rm{Im}}} \end{array}} \right\}\left[ {\rho \int \!\!{\int_{\bar S} {{ n} \cdot { u_r}\left( {i\omega } \right){\phi _k}{\rm{d}}S} } } \right],$

(8)

${C_{rk}} =- \rho \int_{\bar S} { n \cdot { u_r} \cdot g \cdot {\omega _k}{\rm{d}}S} ,$

(9)

流场中辐射波声压为：

$ \begin{array}{l} p\left( {x,y,z,t} \right) =- \rho \sum\limits_{r = 1}^m {\frac{{\partial {\phi _r}}}{{\partial t}}} =- \rho \sum\limits_{r = 1}^m {\left( {i\omega } \right)} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {\frac{1}{{4\pi }}{{\left( {\int {\int_{\bar S} {\sigma \left( Q \right)G\left( {P,Q} \right)dS} } } \right)}_r}} \right)。\end{array}$

(10)

2 桨-轴-壳体计算模型

文中参照基本的潜艇结构在 Abaqus 中建立了单/双层桨-轴-壳体简化模型以及壳体结构与流体接触的湿表面，如图 1 所示。模型结构主要有内外壳体、环肋骨、实肋板、螺旋桨、推进轴系和轴承。单层壳体模型参数与双层模型中内壳体参数一致，而双层壳体模型中实肋板与轻外壳多余质量通过非结构质量添加到单层壳体模型中，以保证单壳体模型与双壳体模型质量相同。螺旋桨为 5 叶三维桨，采用 3D 实体单元模拟；壳体和轴系分别采用 2D 壳单元和 1D 梁单元模拟，环肋骨及实肋板均使用 2D 壳单元模拟；简化模型中包括尾轴后轴承、尾轴前轴承和推力轴承，所有轴承均采用弹簧单元模拟，将尾轴后轴承和尾轴前轴承简化为水平和垂直方向的弹簧，将推力轴承简化为水平、垂向和纵向的弹簧。

3 数值计算及结果分析

潜艇实际航行中，产生的噪声主要有：螺旋桨噪声、水动力噪声和机械噪声等。为较好地模拟 3 种噪声源，文中选择 3 个激励位置施加激励（见图 1），位置 1 作用在螺旋桨桨毂模拟螺旋桨横向和纵向激励力，位置 2 作用在壳体外表面模拟外部流体激励力，位置 3 作用在壳体内部模拟机械设备激励力，力的幅值均为 1 N。在 10 ～150 Hz 频率范围内用三维声弹性响应计算软件 Thafts-acoustic，计算不同激励工况下单/双层模型在无限水深介质中产生的辐射声功率，按公式（11）换算为声源级。

${L_s} = 10\lg \frac{{P/\left( {4\pi } \right)}}{{{P_0}}}。$

(11)

式中：P 为辐射声功率量值； ${P_0} = 0.65 \times {10^{- 18}}\;{\rm{W/Hz}}$ 为基准值 。

激励位置 1 螺旋桨横向力作用下计算得到单/双层桨-轴-壳体结构的声辐射声源级曲线，如图 2 所示。从图中可看出，螺旋桨横向激励下，单/双层水下结构声辐射相差不大，声源级曲线主要在推进轴系以及壳体弯曲模态频率处出现峰值，单/双层水下结构声源级曲线相互交叉，低频段部分峰值频率处双层结构声源级曲线明显高于单层结构，而在 40～80 Hz 频段双层结构声辐射又明显低于单层结构，这主要是由于低频段双层结构内外壳体耦合作用强，振动大。同时，计算得到单/双层水下结构在 10～150 Hz 频段内声辐射总声级分别为 105.3 dB 和 107 dB，因此，螺旋桨横向激励下单层水下结构声辐射总声级略低于双层结构。

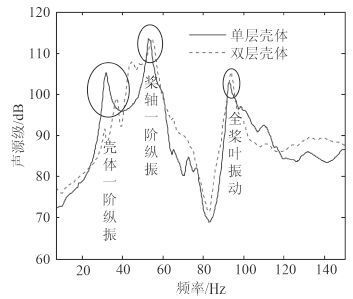
激励位置 1 螺旋桨纵向力作用下计算得到单/双层桨-轴-壳体结构的声辐射声源级曲线，如图 3 所示。从图中可看出，螺旋桨纵向激励下，单/双层水下结构声源级曲线在第一个峰值频率处出现较大变化，这一峰值主要是由于壳体一阶纵振引起的，对于双层结构而言，内外壳体间的实肋板使整个结构的阻抗增加，因此曲线峰值低于单层壳体结构；而第 2 个峰值和第 3 个峰值分别对应桨轴一阶纵振和全桨叶振动，主要受桨轴参数的影响，与壳体结构无关，所以两曲线变化不大。同时，计算得到单/双层水下结构在 10～150 Hz 频段内声辐射总声级分别为 120.2 dB 和 121.8 dB，因此，螺旋桨纵向激励下单层水下结构声辐射总声级略低于双层结构。

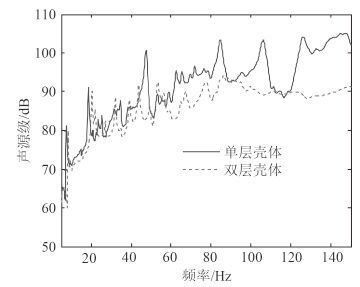
激励位置 2 壳体外表面外部流体激励力作用下计算得到单/双层桨-轴-壳体结构的声辐射声源级曲线，如图 4 所示。从图中可看出，单层结构声辐射声源级曲线高于双层结构，尤其在 60 Hz 以上频段更明显，主要是由于此激励位置处双层结构阻抗明显高于单层结构，能够抑制降低激励引起的声辐射。在低频段，双层壳体声源级曲线峰值频率略高于单壳结构，这主要是因为复杂的双层结构刚度高于单层结构。同时，计算得到单/双层水下结构在 10～150 Hz 频段内声辐射总声级分别为 119.1 dB 和 110.2 dB，因此，外部流体激励下单层水下结构声辐射总声级明显高于双层结构。

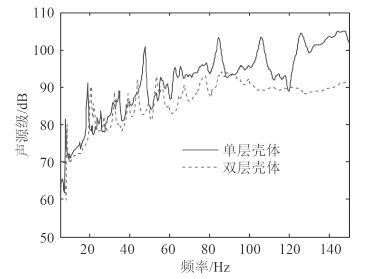
激励位置 3 内部机械设备激励力作用下计算得到单/双层桨-轴-壳体结构的声辐射声源级曲线，如图 5 所示。从图中可看出，单层结构声辐射声源级曲线高于双层结构。计算得到单/双层水下结构在 10～150 Hz 频段内声辐射总声级分别为 119.2 dB 和 110.4 dB，因此，内部机械设备激励下单层水下结构声辐射总声级明显高于双层结构。

4 结语

1）在螺旋桨横向力和纵向力作用下，单/双层水下结构声源级曲线相互交叉，声辐射相差不大，在 10～150 Hz 频段内单层水下结构声辐射总声级略低于双层结构。

2）在外部流体激励力和内部机械设备激励力作用下，单层结构声辐射声源级曲线高于双层结构，因此，在 10～150 Hz 频段内单层水下结构声辐射总声级明显高于双层结构。