潜艇作为一种典型的水下结构物,需要承受巨大的深水压力,它必须有坚固的耐压船体。潜艇上会有多种形式的开孔,用来满足使用的各种实际需求。但是开孔对结构的连续性产生了破坏,壳体强度被削弱,从而需要对开孔附近进行补强,避免在开孔周围造成应力集中现象。因此,对潜艇开孔结构补强问题进行研究很有必要。
圆柱壳是潜艇耐压船体的主要结构形式之一,因此有必要对圆柱壳开孔问题进行研究。圆柱壳的开孔问题也是一个在工程中普遍存在的问题,在压力容器上也很常见[1]。因此,国内工程技术领域普遍关注这个问题,并做了大量的研究,积累了大量文献。朱邦俊和王玉华[2]对开孔圆柱薄壳结构进行了有限元分析;许兵[3]对切断一根肋骨的圆柱壳开孔结构进行了应力分析;周猛猛[4]对围壁补强的圆柱壳开孔结构进行了有限元分析。
本文采用有限元分析的方法,基于 Abaqus 对加筋圆柱壳开孔结构实现了参数化建模并进行应力分析,讨论了多参数对于开孔周围应力的影响。
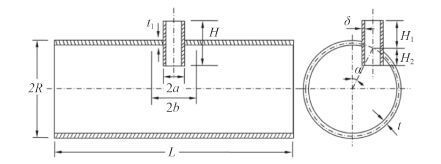
1 典型加筋圆柱壳开孔结构形式加筋圆柱壳开孔多为圆形孔,因此围壁加强结构大多为圆形,可以贯穿至孔内成为双面加强,也可以不贯穿孔内成为单面加强,结构形式示意如图 1 所示。
|
图 1 围壁加强结构形式 Fig. 1 Enclosing wall reinforced structure |
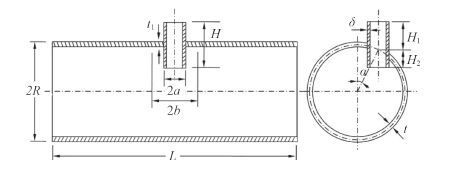
另外,除了使用围壁对孔口进行加强外,还可以采用围壁与复板(嵌入厚板)联合加强的方式,结构形式示意如图 2 所示。
|
图 2 围壁与复板加强结构形式 Fig. 2 Enclosing wall and embedded platereinforced structure |
圆柱壳、加筋和围壁结构均采用壳单元。为了更好的模拟耐压壳的真实情况,采取全结构形式建模,并在围壁上端开孔用板密封,有限元模型见图 3 和图 4。

|
图 3 围壁加强结构有限元模型 Fig. 3 Enclosing wall reinforced structurefinite element model |

|
图 4 围壁和复板加强结构有限元模型 Fig. 4 Enclosing wall and embedded plate reinforced structurefinite element model |
参数化设计是 CAD 技术在实际设计应用中被提炼出来并得到发展的,有着强大实用价值的技术。它是一种利用结构的重要几何参数,应用工况参数及约束参数直接构造和修改有限元模型的方法。
工程实际中很多产品设计都要经过:设计—— 建模—— 分析—— 修改设计—— 再建模—— 再分析,即多次分析的过程。当结构几何尺寸放生改变,就需要重新构建有限元模型,这就使得有限元分析极不方便,导致设计分析效率变低。因此,需要引入参数化的有限元建模思想,简化设计操作,从而达到提高有限元分析效率的目的。
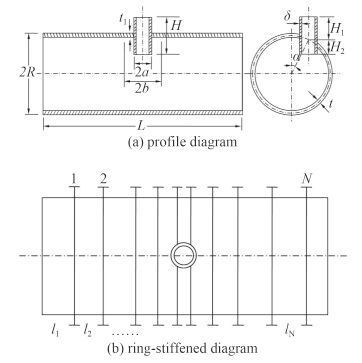
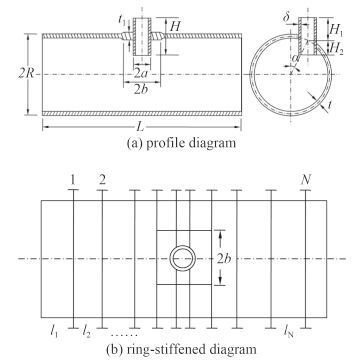
本文提取了典型加筋圆柱壳开孔结构的几何参数和定位参数,例如:耐压船体的几何参数(长度L,半径R 和壳板厚度t);围壁的几何参数(外半径a,高度H 和围壁厚度δ);耐压船体与围壁的相对位置参数(围壁顶端至壳板中心距离H1、H2 和围壁偏斜角度α);复板(嵌入厚板)的几何参数(板宽b 和复板厚度t1);环肋加筋的几何参数和间距。结构参数示意图如图 5 和图 6 所示。结合编程语言 C++ 和 Abaqus 建模语言 Phtyon,实现了加筋圆柱壳开孔结构的参数化建模。
|
图 5 围壁加强结构示意图 Fig. 5 Enclosing wall reinforced structurediagram |
|
图 6 围壁和复板加强结构示意图 Fig. 6 Enclosing wall and embedded platereinforced structurediagram |
本文采用的参数化建模方式,对模型结构进行了简化处理,将圆柱壳、围壁和加筋都采用了壳单元计算分析。为了验证参数化建模方式的准确性,设计了一个圆柱壳开孔围壁补强的结构形式,结构的具体参数如表 1 所示,计算压力为 0.1 MPa。并将有限元分析的结果与参考《潜艇结构设计计算方法》中耐压船体圆形开孔结构强度的经验计算公式得出的结果进行对比。
|
|
表 1 结构具体参数 Tab.1 Structure specific parameter |
参考《潜艇结构设计计算方法》第 10 章耐压船体圆形开孔结构强度,根据其中规定的经验公式(1)~ 式(6)计算出开孔周边最大应力。
| $\xi =1.285H\sqrt{a\delta },$ | (1) |
| $ \eta = c/H, $ | (2) |
| $ c = {c_2} + 0.5R\left\{ {1- \cos \left[ {\arcsin \left( {a/R} \right)} \right]} \right\}, $ | (3) |
| $ {A_c} = \xi \delta \sqrt {a\delta } + t\delta , $ | (4) |
| $ {\sigma _\theta } = \frac{{pR}}{t}, $ | (5) |
| $ {\sigma _{\theta \max }} = {K_\sigma }{\sigma _\theta }。 $ | (6) |
式中:ξ 为参数;H 为围壁高度,mm;a 为开孔半径,mm;δ 为围壁计算厚度,mm;η 为参数;c 为围壁短端边缘至壳板中心 2 个距离c1 和c2 的平均值,mm;R 为耐压船体半径,mm;Ac 为相当围壁面积,mm2;σθ 为环向薄膜应力,MPa;p 为计算压力,MPa;t 为耐压圆柱壳厚度,mm;σθmax 为孔边最大应力,MPa。
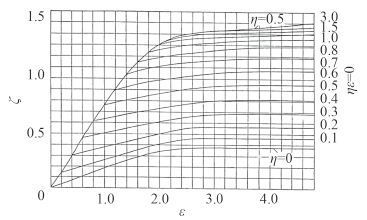
围壁有效高度系数ζ 通过图 7 插值可得。
|
图 7 围壁有效高度系数 Fig. 7 Enclosing wall Effective height coefficient |
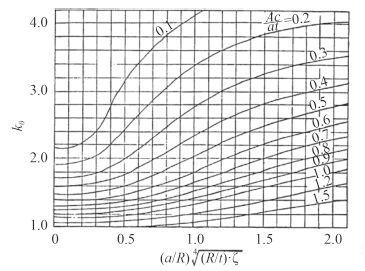
孔边壳板应力集中系数Kσ 通过图 8 插值可得。
|
图 8 孔边壳板应力集中系数 Fig. 8 Hole edge plate stress concentration coefficient |
中间计算结果如表 2 所示。
|
|
表 2 中间计算结果 Tab.2 Intermediate calculation results |
将采用本文参数化建模有限元分析求出的孔边最大应力与通过经验公式计算出的结果进行比较,如表 3 所示。
|
|
表 3 对比结果 Tab.3 Comparison result |
由对比分析可知,本文采用的参数化建模分析方式有一定的准确性,能够满足工程设计的需求。
4 结构参数对应力集中的影响应力集中现象普遍存在于各种工程结构中,大部分结构破坏事故是由应力集中引起的。为确保工程结构的使用安全,提高产品的质量和经济效益,必须科学地处理结构元件的应力集中问题。加筋圆柱壳开孔对结构的连续性产生了破坏,壳体强度被削弱,开孔周围容易产生应力集中现象。
本章主要研究围壁尺寸、嵌入厚板的尺寸和肋骨的参数对于开孔周围应力集中的影响。
4.1 围壁尺寸为了研究围壁高度H 和围壁厚度δ 对开孔周围应力集中的影响,参数化建模计算L = 5 000 mm,R = 2 500 mm,t = 10 mm,a = 250 mm,α = 0°,δ = 20~40 mm,H1 = 100~300 mm,H2 = 100~300 mm,共 15 个系列模型。
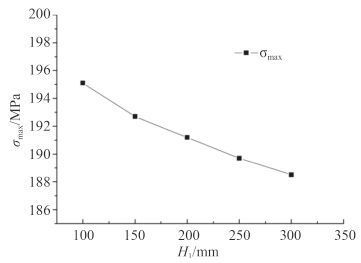
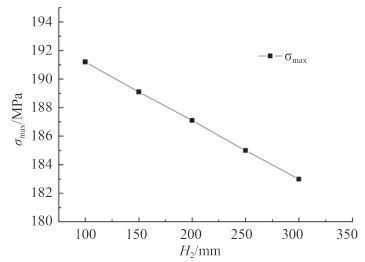
4.1.1 围壁高度围壁高度分为壳外围壁顶端至壳板中心线高度H1 和壳内围壁顶端至壳板中心线高度H2,在研究H1 对开孔周围应力集中的影响时,H2 取值 100 mm;在研究H2 对开孔周围应力集中的影响时,H1 取值 200 mm。高度H1 对开孔周围应力集中的影响如图 9 所示。高度H2 对开孔周围应力集中的影响如图 10 示。
|
图 9 高度H1 对开孔周围应力集中的影响 Fig. 9 Effect of heightH1 on the stress concentration around the open hole |
|
图 10 高度H2 对开孔周围应力集中的影响 Fig. 10 Effect of heightH2 on the stress concentration around the open hole |
由图 9 可知,随着H1 的增加,开孔周围最大应力值随之下降。因此,在设计过程中,H1 的高度应在许可范围内选取最大值。
由图 10 可知,随着H2 的增加,开孔周围最大应力值随之下降。因此,在设计过程中,H2 的高度应在许可范围内选取最大值。
4.1.2 围壁厚度在研究围壁厚度对开孔周围应力集中的影响时,H1 取值 200 mm,H2 取值 100 mm。围壁厚度δ 对开孔周围应力集中的影响如图 11 示。
|
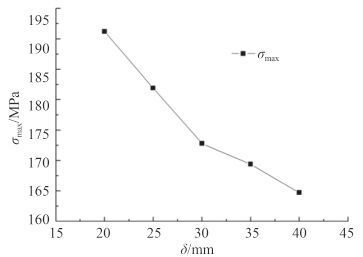
图 11 厚度δ 对开孔周围应力集中的影响 Fig. 11 Effect of thicknessδ on the stress concentration around the open hole |
由图 11 知,随着δ 的增加,开孔周围最大应力值随之下降。因此,在设计过程中,δ 的值应在许可范围内选取最大值。
4.2 嵌入厚板的尺寸为了研究嵌入厚板的半宽b 和厚度t1 对开孔周围应力集中的影响,参数化建模计算L = 5 000 mm,R = 2 500 mm,t = 10 mm,a = 250 mm,α = 0°,δ = 20 mm,H1 = 200 mm,H2 = 100 mm,b = 700~1 100 mm,t1 = 20~40 mm 共 10 个系列模型。
4.2.1 嵌入厚板半宽在研究嵌入厚板半宽b 对开孔周围应力集中的影响时,t1 取值 20 mm。嵌入厚板半宽b 对开孔周围应力集中的影响如图 12 所示。
|
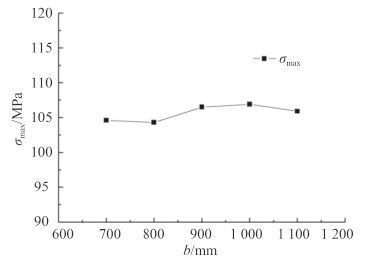
图 12 半宽b 对开孔周围应力集中的影响 Fig. 12 Effect of half-widthb on the stress concentration around the open hole |
由图 12 可知,嵌入厚板半宽b 对于开孔周围应力集中影响不大。因此,在设计过程中,b 的值可在满足大于 2 倍开孔半径的情况下参考其他因素选取合适的数值。
4.2.2 嵌入厚板厚度在研究嵌入厚板厚度t1 对开孔周围应力集中的影响时,b 取值 1 000 mm。嵌入厚板厚度t1 对开孔周围应力集中的影响如图 13。
|
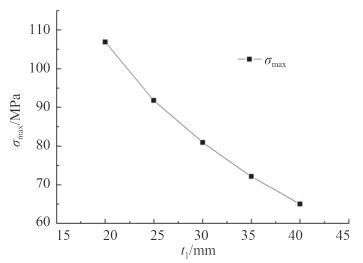
图 13 厚度t1 对开孔周围应力集中的影响 Fig. 13 Effect of thicknesst1 on the stress concentration around the open hole |
由图 13 可知,随着t1 的增加,开孔周围最大应力值随之下降。因此,在设计过程中,t1 的值应在许可范围内选取最大值。
5 结语1)本文编写的参数化建模程序,设计变量较多较全面,能够很好地完成典型耐压船体开孔结构的建模工作,提高了设计工作效率,分析结果与规范计算结果吻合良好。
2)本文讨论了多个参数对于开孔周围应力集中的影响,分析得出围壁高度、围壁厚度和嵌入厚板的厚度对于开孔周围应力的影响较大,随着围壁高度、围壁厚度和嵌入厚板的厚度的增加,开孔周围应力减小;而嵌入厚板的半宽对于开孔周围的应力几乎没有影响,随着厚度的变化,开孔周围应力变化很小,为设计工作提供了参考。
| [1] | 施涛. 典型耐压船体开孔加强结构优化设计[D]. 武汉: 华中科技大学, 2012 |
| [2] | 朱邦俊, 王玉华. 开孔圆柱薄壳结构有限元分析[J]. 计算结构力学及其应用 , 1984, 1 (3):91–98. |
| [3] | 许兵. 切断一根肋骨的圆柱壳开孔应力分析[J]. 舰船科学技术 , 2004, 26 (S):13–17. |
| [4] | 周猛猛, 杨宇华, 耿黎明, 等. 围壁补强的圆柱壳开孔结构有限元分析[J]. 船海工程 , 2014, 43 (2):4–6. |
 2017, Vol. 39
2017, Vol. 39
