在海洋复杂环境下,水面舰艇作为海平面上凸出的至高点,极易受到雷电的直接危害。为了避免直击雷的伤害,水面舰艇在桅顶至高点设计安装了避雷针,通过避雷针将直击雷电流导入海洋,保护舰面设备不会受到直击雷的危害。
避雷针对于提高水面舰艇的雷电防护能力,提高舰艇安全性具有重要的意义,由于避雷针需要安装在舰艇至高点,因此开展避雷针设计时需要考虑避雷针对桅顶天线,尤其是对天线方向图的影响。天线的辐射方向图(简称方向图)是天线的辐射参量随空间方向变化的图形表示。所谓辐射参量包括辐射的功率通量密度、场强、相位和极化,在通常情况下,辐射方向图在远区测定,并表示为空间方向坐标的函数[1]。
天线方向图是天线最重要的性能指标之一,因此本文通过仿真计算等手段,以某型舰桅顶天线与避雷针的安装设计情况为例,仿真分析避雷针对桅顶天线方向图的影响,评估避雷针对设备战绩指标的影响程度,以确保桅顶设备与避雷针一体化安装设计的情况下能够正常工作。
1 相控阵天线方向图的全波仿真分析方法矩量法是一种求解线性方程的方法[2]。如下式:
| $L(f) = g,$ | (1) |
式中:L为线性算子;g为已知函数;f为未知函数。令f在L的定义域中展开为f1, f2, f3……的组合,如下式:
| $f = \sum\limits_n {{\alpha _n}} {f_n},$ | (2) |
式中:
| $\sum\limits_n {{\alpha _n}} L({f_n}) = g。$ | (3) |
对此问题若已经规定了一个适当的内积
| $\begin{array}{l} \sum\limits_n {{\alpha _n} < {\omega _m},} L({f_n}) > = < {\omega _m},g > , m = 1,2,3 \cdots \end{array}$ | (4) |
此方程组可以写成如下矩阵形式:
| ${\mathit{\boldsymbol{l}}_{mn}}{\mathit{\boldsymbol{\alpha }}_n} = {\mathit{\boldsymbol{g}}_m},$ |
式中:
| ${\mathit{\boldsymbol{l}}_{mn}} = \left[ {\begin{array}{*{20}{c}} { < {\omega _1},L{f_1} > }&{ < {\omega _1},L{f_2} > }&{ \ldots \ldots }\\ { < {\omega _2},L{f_1} > }&{ < {\omega _2},L{f_2} > }&{ \ldots \ldots }\\ { \ldots \ldots }&{ \ldots \ldots }&{ \ldots \ldots } \end{array}} \right]{\rm{ }},$ |
| ${\mathit{\boldsymbol{\alpha }}_n} = \left[ {\begin{array}{*{20}{c}} {{\alpha _1}}\\ {{\alpha _2}}\\ { \ldots \ldots } \end{array}} \right],$ |
| ${\mathit{\boldsymbol{g}}_m} = \left[ {\begin{array}{*{20}{c}} { < {\omega _1},g{\rm{ }} > }\\ { < {\omega _2},g > }\\ { \ldots \ldots } \end{array}} \right]{\rm{ 。}}$ |
如果
| ${\mathit{\boldsymbol {\alpha} _n}} = {{\mathit{\boldsymbol {l}_{mn}}}^{ - 1}}{\mathit{\boldsymbol {g}_m}}。$ | (5) |
在计算电磁学中,一般把未知的面电流密度J展开为:
| $J = \sum\limits_n {{I_n}} {J_n} ,$ |
式中
| $\sum\limits_n {{I_n} < {W_m},} L({J_n}) > = < {W_m},{E^i} > , $ |
式中$ < f, g > $表示取f与g的内积。上式可写为更易于理解的表达式:
| ${\mathit{\boldsymbol {Z}_{mn}}}{\mathit{\boldsymbol {I}_{mn}}} = {\mathit{\boldsymbol {V}_m}} ,$ | (6) |
其中
在严格的矩量法步骤中,应当把所处理问题中的所有物体都取走而代之以自由空间辐射的等效电磁流[3]。因此,当要求出第m个检验函数对第n个基函数产生的场的反应时,只需要考虑通过最短的自由空间路程直接到达第m个检验函数的场,因为这是唯一可能有的场。但如果在某种情况下把所处理问题中部分物体保留下来而不用等效电磁流取代它,则阻抗矩阵元素的计算更复杂。假设
| ${{\mathit{\boldsymbol {Z}_{mn}}}^{'}} = < {W_m},aL({J_n}) + bL({J_n}) > ,$ | (7) |
式中
| ${{\mathit{\boldsymbol {Z}_{mn}}}^{'}} = < {W_m},aL({J_n}) + bL({J_n}) > = {Z_{mn}} + Z_{mn}^g 。$ | (8) |
式中上标g表示
广义电压矩阵元素也应该修正为
| ${{\mathit{\boldsymbol {V}_m}}^{'}} = < {W_m},({E^i} + {C_m}{E^i}) > ,$ | (9) |
式中:
于是:
| $\begin{array}{l} {{\mathit{\boldsymbol{V}_m}}^{'}} = < {W_m},({E^i} + {C_m}{E^i}) > = < {W_m},{E^i} > + < {W_m},{C_m}{E^i} > \end{array} \text{,}$ | (10) |
因此,式(6)可修正为:
| ${Z^{'}}{I^{'}} = {V^{'}} 。$ | (11) |
其中
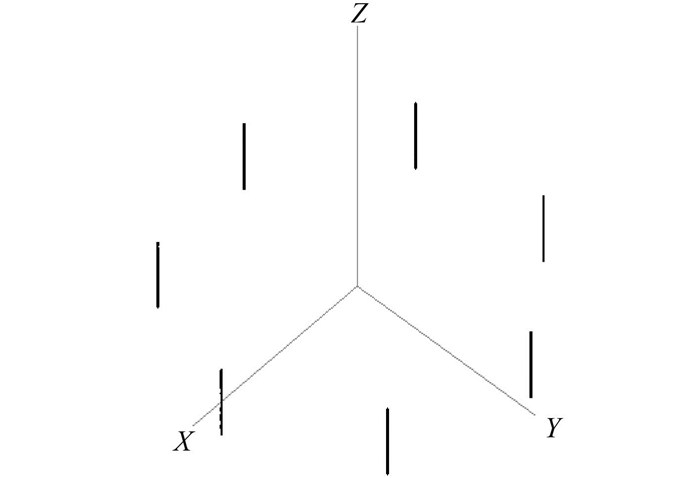
采用矩量法进行计算需要对天线模型, 按照0.2λ进行剖分,建模如图 1所示。
|
图 1 天线仿真模型 Fig. 1 Simulation model of antenna |
为尽量扩大雷电防护范围,改善避雷效果,避雷针应该制高点安装。为了分析避雷针对天线阵方向图的影响,本文分别建立无避雷针和有避雷针的预测仿真模型,对比2种情况下方位面和俯仰面的天线方向图,评估避雷针对天线的影响。某型舰桅顶天线阵无避雷针的仿真模型如图 1所示。
为了评估避雷针对天线的影响,选择天线的1个工作频点作为典型工作频点,仿真分析有无避雷针时方向图(见图 2~图 4)。
|
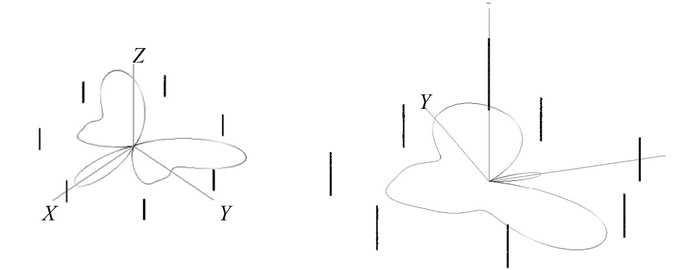
图 2 阵子天线阵有无避雷针时方位面方向图对比 Fig. 2 The azimuth pattern comparation of the antenna with or without lightnening rod |
|
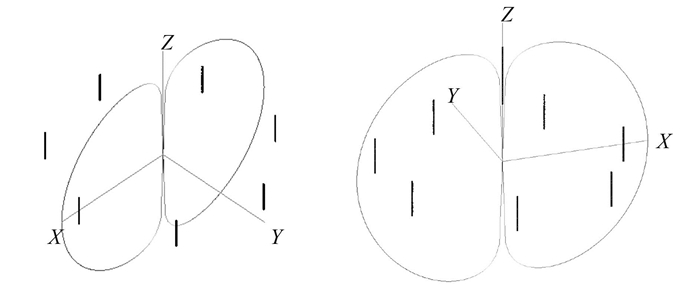
图 3 阵子天线阵有无避雷针俯仰面方向图对比 Fig. 3 The pitching pattern comparation of the antenna with or without lightnening rod |

|
图 4 阵子天线阵有无避雷针立体方向图对比 Fig. 4 The 3D pattern comparation of the antenna with or without lightnening rod |
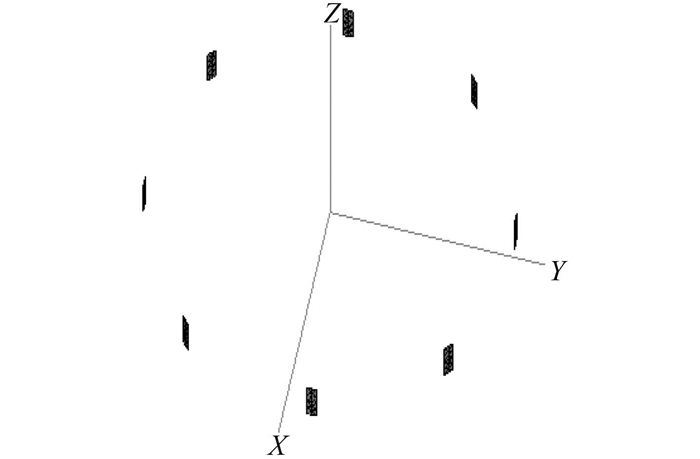
面天线阵仿真模型如图 5所示,面片采用RWG方式剖分[4]。选择1个典型工作频率开展仿真计算,分析避雷针对天线的影响(见图 6~图 8)。
|
图 5 天线仿真模型 Fig. 5 Simulation model of antenna |
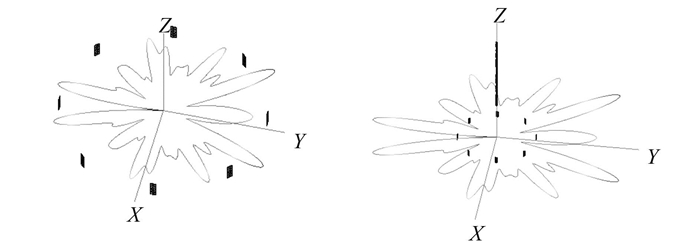
|
图 6 面天线阵有无避雷针方位面方向图对比 Fig. 6 The azimuth pattern comparation of the antenna with or without lightnening rod |
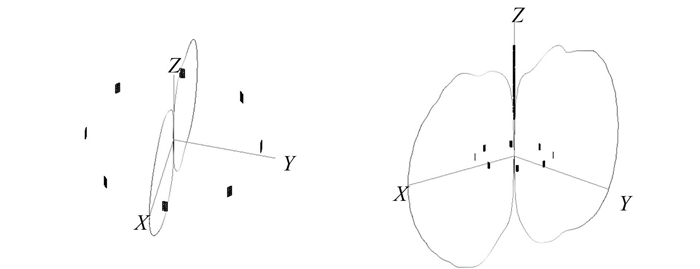
|
图 7 面天线阵有无避雷针俯仰面方向图对比 Fig. 7 The pitching pattern comparation of the antenna with or without lightnening rod |
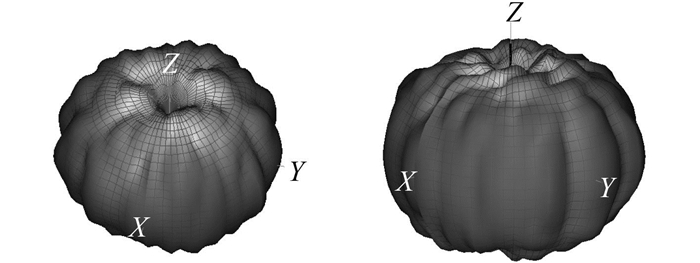
|
图 8 面天线阵有无避雷针立体方向图对比 Fig. 8 The 3D pattern comparation of the antenna with or without lightnening rod |
图 9为阵子天线阵有无避雷针时俯仰面方向图对比,图 10为各方向增益变化对比。
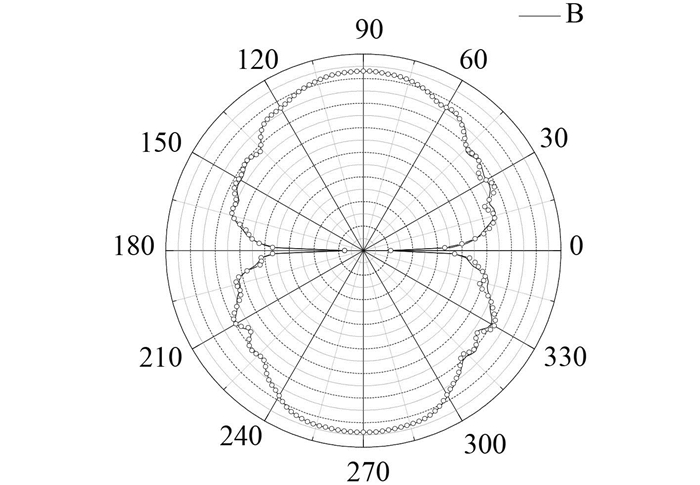
|
图 9 阵子天线阵有无避雷针时俯仰面方向图对比 Fig. 9 The pitching pattern comparation of the antenna with or without lightnening rod |
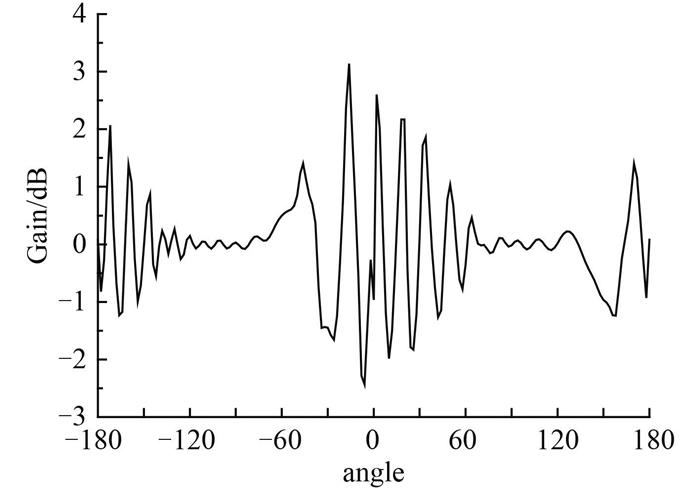
|
图 10 阵子天线阵有无避雷针时各方向增益变化 Fig. 10 The gain error of the antenna with or without lightnening rod |
通过图 10可看出,在设备主要关心的±90°附近角域,增益几乎没有变化;0°角区域增益几乎为0,增益的变化不会影响设备作战使用。因此通过上述分析可以看出,该避雷针设计方案不影响设备正常工作,具有较好的工程可行性。
5 结语作者采用矩量法,建立了天线和避雷针的仿真模型,仿真分析有无避雷针时天线方向图,对比分析天线增益的变化,评估设备的受影响程度,分析避雷针设计方案的可行性,确保设备不会因加装避雷针而影响战技指标。
| [1] | 魏文元, 宫德明, 陈必森, 等. 天线原理[M]. 北京: 国防工业出版社, 1985. |
| [2] | HARRINGTON R F. Field computation by moment methods[M]. New York: MacMillan, 1968. |
| [3] | 哈林登R F.计算电磁场的矩量法[M].王尔杰, 译.北京:国防工业出版社, 1981. |
| [4] | RAO S M, WILTON D R, GLISSON A W. Electromagnetic scattering by surfaces of arbitrary shape[J]. IEEE Transactions on Antennas and Propagation , 1982, 30 (3) :409–418. DOI: 10.1109/TAP.1982.1142818 |
 2016, Vol. 38
2016, Vol. 38
