2. 国防科学技术大学, 湖南 长沙 410073
2. National University of Defense Technology, Changsha 410073, China
GPS(北斗)卫星系统有着全覆盖、全天候工作、用途广和精度高的优点。目前,美国已经把GPS(北斗)广泛地应用于陆、海、空各种机动平台的导航定位中,在现代战场上发挥着至关重要的作用。对于潜艇来说,无论是进行系统重调还是动基座对准,都需要接收来自外部的卫星导航信息。然而,现代海洋战场上电磁环境十分复杂,敌我双方电磁对抗日益激烈,加上各种因素的干扰,潜艇接收到的卫星导航信息中很有可能引入误差过大的信息,称为坏值。这些坏值会直接危害到惯导系统的修正过程,导致结果产生重大偏差[1-3]。因此,在系统修正时必须考虑到坏值的影响。为了解决这些问题,必须提出可行的卫星导航抗干扰方案。我们可以设计检测坏值以及隔离坏值的算法来加强修正过程的动态适应性及容错性。本文主要采用基于卡尔曼滤波器残差信息的坏值检测方法,对GPS(北斗)导航信息进行坏值检测并合理隔离[4-5]。
1 卡尔曼滤波模型设由姿态、速度、位置误差以及陀螺、加速度计零偏误差方程组成的惯导系统的误差方程为[6-7]:
| $\left\{ {\begin{array}{*{20}{l}} {\dot \varphi = - \omega _{in}^n \times \varphi + \delta \omega _{ie}^n + \delta \omega _{en}^n - C_b^n\left( {\varepsilon _b^b + \varepsilon _\omega ^b} \right){\rm{,}}}\\ {\delta {{\dot v}^n} = - \varphi \times {f^n} - \left( {2\omega _{ie}^n + \omega _{en}^n} \right) \times \delta {v^n} - }\\ {\quad \quad \left( {2\delta \omega _{ie}^n + \delta \omega _{en}^n} \right) \times {v^n} + C_b^n\left( {\nabla _b^b + \nabla _\omega ^b} \right){\rm{,}}}\\ {\delta \dot L = \frac{{\delta {v_N}}}{{{R_M} + h}} - \frac{{{v_N}\delta h}}{{{{\left( {{R_M} + h} \right)}^2}}}{\rm{,}}}\\ {\delta \dot \lambda = \frac{{\delta {v_E}}}{{\left( {{R_N} + h} \right)\cos L}} + \frac{{{v_E}\sin L\delta L}}{{\left( {{R_N} + h} \right){{\cos }^2}L}} - \frac{{{v_E}\delta h}}{{{{\left( {{R_N} + h} \right)}^2}\cos L}}{\rm{,}}}\\ {\delta \dot h = \delta {v_U}{\rm{。}}} \end{array}} \right. $ | (1) |
式中:
根据上述误差模型,可设卡尔曼滤波器的状态量为:
| $x = {\left[ {{\varphi ^{\rm{T}}}\;\;\delta {v^{n{\rm{T}}}}\;\;\delta {P^{\rm{T}}}\;\;\varepsilon _b^{b{\rm{T}}}\;\;\nabla _b^{b{\rm{T}}}} \right]^{\rm{T}}},$ | (2) |
则卡尔曼滤波器的系统方程为:
| $\dot x\left( t \right) = F\left( t \right)x\left( t \right) + \mathit{\Gamma }\left( t \right)\omega \left( t \right){\rm{。}}$ | (3) |
设惯导在n系下速度和位置输出分别为
| $z = \left[ {\begin{array}{*{20}{l}} {v_{{\rm{INS}}}^n - v_{{\rm{GPS}}}^n}\\ {{P_{{\rm{INS}}}} - {P_{{\rm{GPS}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {\delta {v^n}}\\ {\delta P} \end{array}} \right] - \left[ {\begin{array}{*{20}{l}} {\delta v_G^n}\\ {\delta {P_G}} \end{array}} \right] = Hx + {V_{vp}}{\rm{。}}$ | (4) |
式中:
采用“速度+位置”匹配的卡尔曼模型,能够最大程度地利用GPS(北斗)的有效信息,提高精度,缩减时间。
2 GPS(北斗)信号的残差χ2检验法残差χ2检验法的基本思路是[3]:如果在第k-1步以前系统无故障,即接收到的信息无误,那么经过卡尔曼滤波得到第k-1步的估计值
| ${\hat x_{k,k - 1}} = {\varphi _{k,k - 1}}{\hat x_{k - 1}}{\rm{,}}$ | (5) |
则第k时刻系统测量的预测量为:
| ${\hat z_{k,k - 1}} = {H_k}{\hat x_{k,k - 1}}{\rm{。}}$ | (6) |
如果第k时刻系统也正常工作,则实际量测值zk应该正确,那么实际量测值zk与预测值
| $\begin{array}{*{20}{l}} \begin{array}{l} E\left[ {{r_k}} \right] = E\left[ {{z_k} - {{\hat z}_{k,k - 1}}} \right] = \\ \quad \quad \quad {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} E\left[ {{H_k}\left( {{{\hat x}_k} - {{\hat x}_{k,k - 1}}} \right)} \right] + E\left[ {{v_k}} \right] = 0, \end{array} \end{array}$ | (7) |
| $\begin{array}{l} {S_k} = E\left[ {{r_k}r_k^{\rm{T}}} \right] = HE\left[ {\left( {{{\hat x}_k} - {{\hat x}_{k,k - 1}}} \right){{\left( {{{\hat x}_k} - {{\hat x}_{k,k - 1}}} \right)}^{\rm{T}}}} \right]H_k^{\rm{T}} = \\ \;\;\;\;\;\;\;\;{H_k}{P_{k/k - 1}}H_k^{\rm{T}} + {R_k}。 \end{array}$ | (8) |
因此可知,若系统没有发生故障,那么残差rk服从零均值高斯白噪声分布;若系统发生故障,那残差rk不会服从零均值高斯白噪声分布。所以可通过检测rk的统计学特性来判断系统发生故障的可能。进一步根据统计学中假设检验的理论,可构造方差检测的统计量为λk,且
| ${\lambda _k} = r_k^{\rm{T}}S_k^{ - 1}{r_k}{\rm{,}}$ | (9) |
则系统正常工作时,λk服从自由度为m的χ2分布;而发生故障时,λk不再服从这种分布。据此,可以设置恰当的误警概率α,通过χ2的分布函数表可以查出χ2分布相对误警率α的临界值TD。正常情况下,α是小量,对应λk > TD的事件应当是小概率事件,所以如果计算得到λk > TD就可以判断这时候的GPS(北斗)量测量是坏值,可以把它从有效量测里剔除。
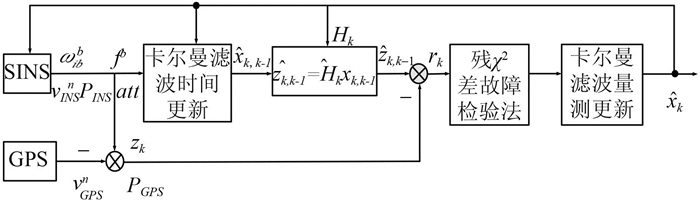
综上,可以得到以下的坏值判定准则:若λk≥TD,判定GPS(北斗)量测出现坏值;若λk < TD,判定GPS(北斗)工作正常。其中,λk为坏值检测函数;TD为检测门限;α为误警率。则GPS(北斗)信号残差χ2检验流程图如图 1所示。
|
图 1 残差法检验流程图 Fig. 1 The flow chart of residual examine method |
利用Matlab软件模拟基于INS/GPS(北斗)的组合导航系统下的载体运动过程,并在运动过程中向GPS(北斗)导航信息中引入了坏值。对经过了坏值检测与剔除以及未经过坏值检测与剔除的导航结果进行比较。
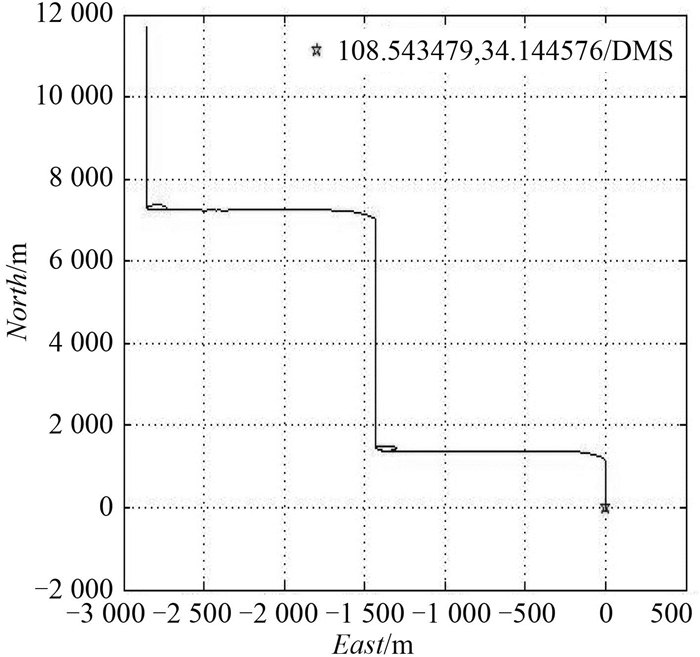
3.1 引入坏值之后的导航结果在仿真程序中,设定每隔500 s时间,在GPS(北斗)所提供位置信息中的经度、纬度信息中引入1角分的误差,则组合导航轨迹如图 2所示。可以看出,导航轨迹周期性地发生不正常的跳动,坏值对导航轨迹产生了比较明显的影响。

|
图 2 引入坏值后的组合轨迹图 Fig. 2 The trajectory with bad values |
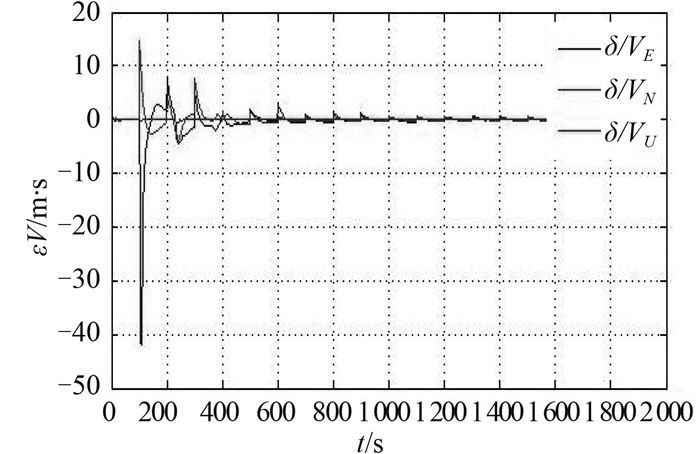
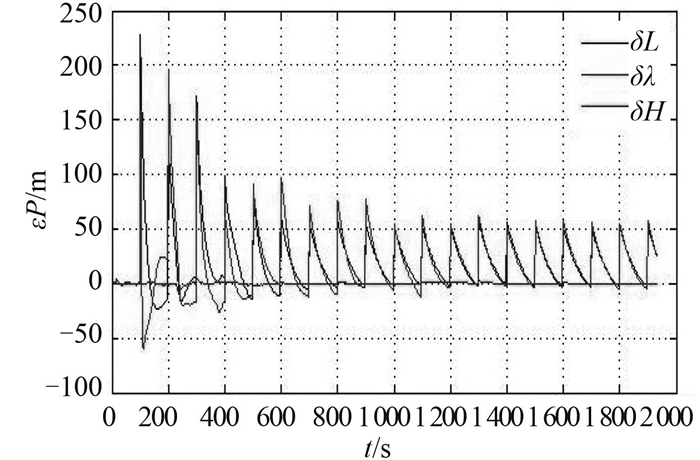
由图 2可看出,东向速度和北向速度误差逐渐收敛到0,但仍可以看到过程中周期性地出现跳点且速度误差最大值可达到42 m/s,这显然是坏值对速度误差的干扰引起的。由图 3可以看出,位置误差虽然在捷联惯导系统的作用下跳动幅度减小,但经度、纬度误差最大值仍可达到230 m左右,且误差无法收敛到0。
|
图 3 引入坏值后的速度误差图 Fig. 3 The velocity error with bad values |
|
图 4 引入坏值后的位置误差图 Fig. 4 The position error with bad values |
采用卡尔曼滤波的残差χ2检验法进行坏值检验并剔除坏值后,同修正前的导航轨迹相比,修正后的导航轨迹更加平滑,东西向的跳动减少了100 m左右,更贴近实际导航结果。
|
图 5 修正后的组合导航轨迹图 Fig. 5 The trajectory after correction |
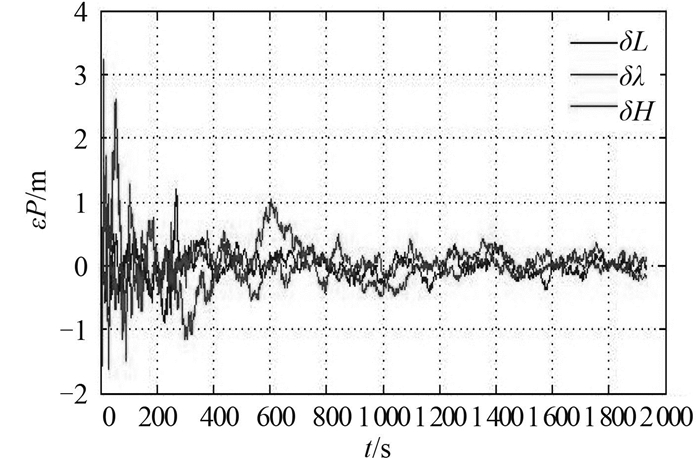
由图 5可看到,修正后各方向速度误差变化范围远小于修正前,修正后的最大值只有0.3 m/s,比修正前精度提高了99.3%,且迅速收敛到0,没有发生跳变。由图 6可看到,位置误差范围在-2~4 m之间,远小于修正前的-50~250 m,位置误差逐渐收敛,结果得到了明显的修正。

|
图 6 修正后的速度误差图 Fig. 6 The velocity error after correction |
|
图 7 修正后的位置误差图 Fig. 7 The position error after correction |
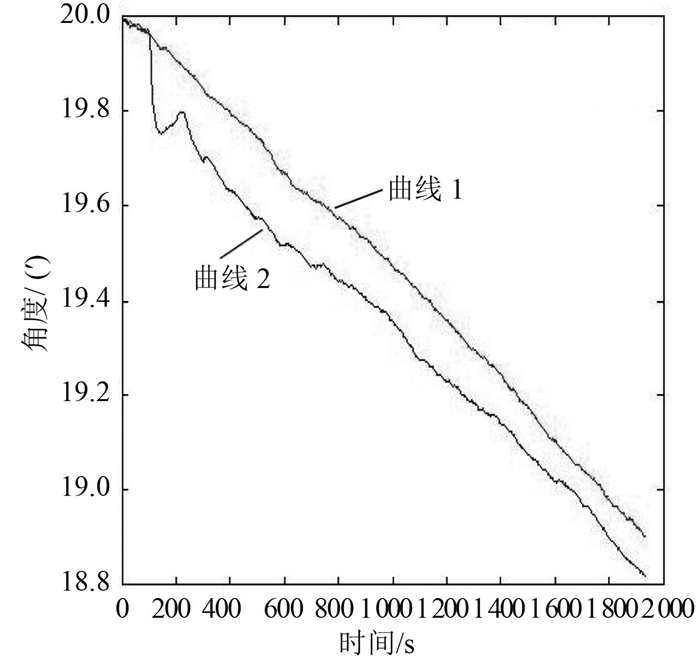
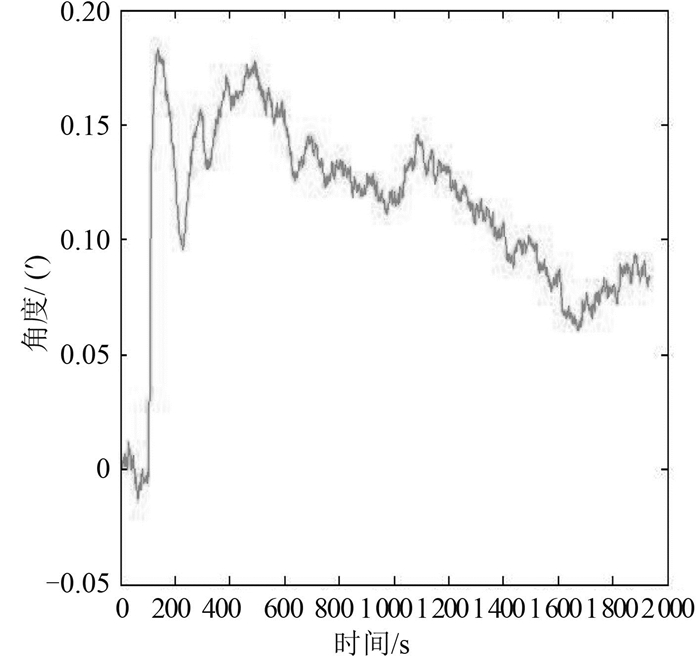
图 8为修正前后航向角对比图。其中,曲线1为引入坏值后的航向角,曲线2为修正后的航向角,两者做差可得图 9。可以看出,航向角得了到最大0.18′的修正,修正效果很明显。
|
图 8 修正前后航向角对比图 Fig. 8 The comparison of heading before and after correction |
|
图 9 修正前后航向角差值图 Fig. 9 The difference of heading before and after correction |
仿真表明,利用GPS(北斗)信号的残差χ2检验法检测和剔除GPS(北斗)信号中的坏值信息对导航结果的修正作用十分明显。一方面能够极大地减小速度及位置误差,尤其是速度误差修正可达几十米每秒。另一方面对潜艇的航向角误差也产生了明显的约束作用,修正幅度可达到角分量级。总而言之,这种方法提高了激光惯导系统重调过程中的动态适应性,起到了抗干扰的作用。
4 结语本文以激光陀螺惯导系统对准及导航过程中接收卫星信息进行导航信息校正为背景,仿真验证了利用卫星信号的残差χ2检验法检测和剔除卫星信号中坏值信息的有效性,保证了艇载激光惯导在复杂海洋电磁环境下的重调可靠性。
| [1] | 康博.北斗导航系统空时抗干扰技术研究[D].西安:西安理工大学, 2013. |
| [2] | 胡源. 导航战中的GPS干扰研究[J]. 空间电子技术 , 2009, 6 (4):48–52. |
| [3] | 薛广龙.惯导系统信息可靠性估计与故障诊断方法[D].哈尔滨:哈尔滨工程大学, 2012. http://cn.bing.com/academic/profile?id=e9ae7df981b5111eae383c0d78f2a4f7&encoded=0&v=paper_preview&mkt=zh-cn |
| [4] | 吴枫, 秦永元, 张金亮, 等. GPS坏值检测在弹载惯导空中对准中的应用[J]. 测控技术 , 2014, 33 (1):137–140. |
| [5] | ROGERS R M. Applied mathematics in integrated navigation systems[M]. 2nd ed. American:American Institute of Aeronautics and Astronautics, Inc., 2003:41-43. |
| [6] | 廖明.舰载捷联惯导系统虚拟试验平台设计与实现[D].南京:东南大学, 2011. |
| [7] | GREWAL M S, HENDERSON V D, MIYASAKO R S. Application of Kalman filtering to the calibration and alignment of inertial navigation systems[J]. IEEE Transactions on Automatic Control , 1991, 36 (1) :3–13. DOI: 10.1109/9.62283 |
 2016, Vol. 38
2016, Vol. 38
