随着鱼雷自导技术的发展,现代鱼雷已普遍具备了对目标的尺度识别能力。在水声对抗领域,鱼雷对抗器材也从常用的噪声或应答式点源模拟器发展到尺度式目标模拟器。如何提高目标特性模拟真实程度的研究和实践非常必要,对水下目标方位距离进行实时测量是提高声学目标模拟器对尺度目标模拟逼真程度的一个先决条件。
目前水下尺度目标模拟一般采用水面船只或水下航行体拖曳线列阵方式,线列阵阵长通常为几十米到一百米,基于基阵物理特性,需利用短基线定位系统原理,通过测量声波在目标与各个阵元之间的到达时差来解算目标方位和距离,完成水下目标定位[1]。
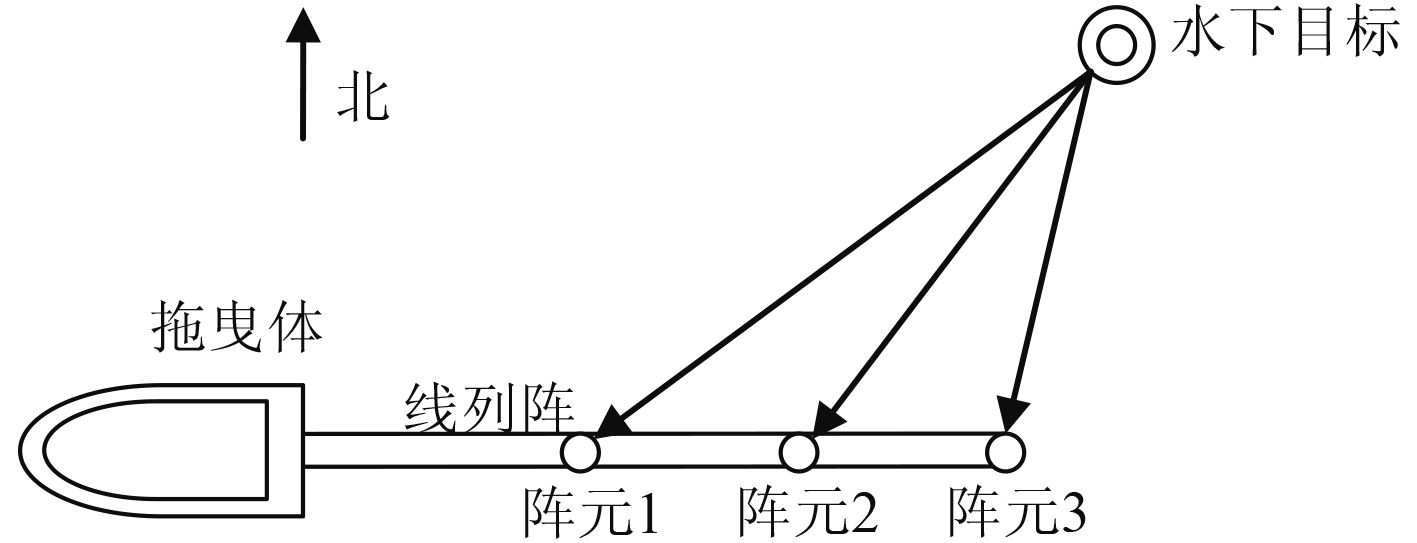
本文所述线列阵定位系统的工作态势示意如图 1所示。系统工作时,线列阵上的3个或更多个换能器接收水下目标发射的脉冲信号,模拟接收机放大滤波后的信号转换为数字信号,线列阵定位系统信号处理设备实时检测数字信号,并估计信号频率、时延值、幅度、脉宽等参数,求得目标的方位和距离。
|
图 1 系统工作态势示意图 Fig. 1 Schematic diagram of system working situation |
到达时差方法是最常用的水声被动定位算法之一,该算法根据到达水听器阵列不同阵元的信号相对时延来进行目标方位和距离参数的估计[1],基本原理是利用时延采用双曲交汇来定位。基于到达时差法的被动定位系统的精度高低与基阵孔径大小有着密切的关系。通常情况下,基阵的孔径越大,定位精度越高[2]。本文线列阵基阵长度属于短基线定位系统,水下目标入射方位可以采用时差原理进行定位,求解2个时差确定的双曲线方程组结果,会得到关于线列阵对称的2个方位值,也就是说时差原理定位无法知道水下目标入射方位是处于线列阵左舷还是右舷[3],但定位的目的是为时变目标强度的设定提供舷角参数,所以不受影响。
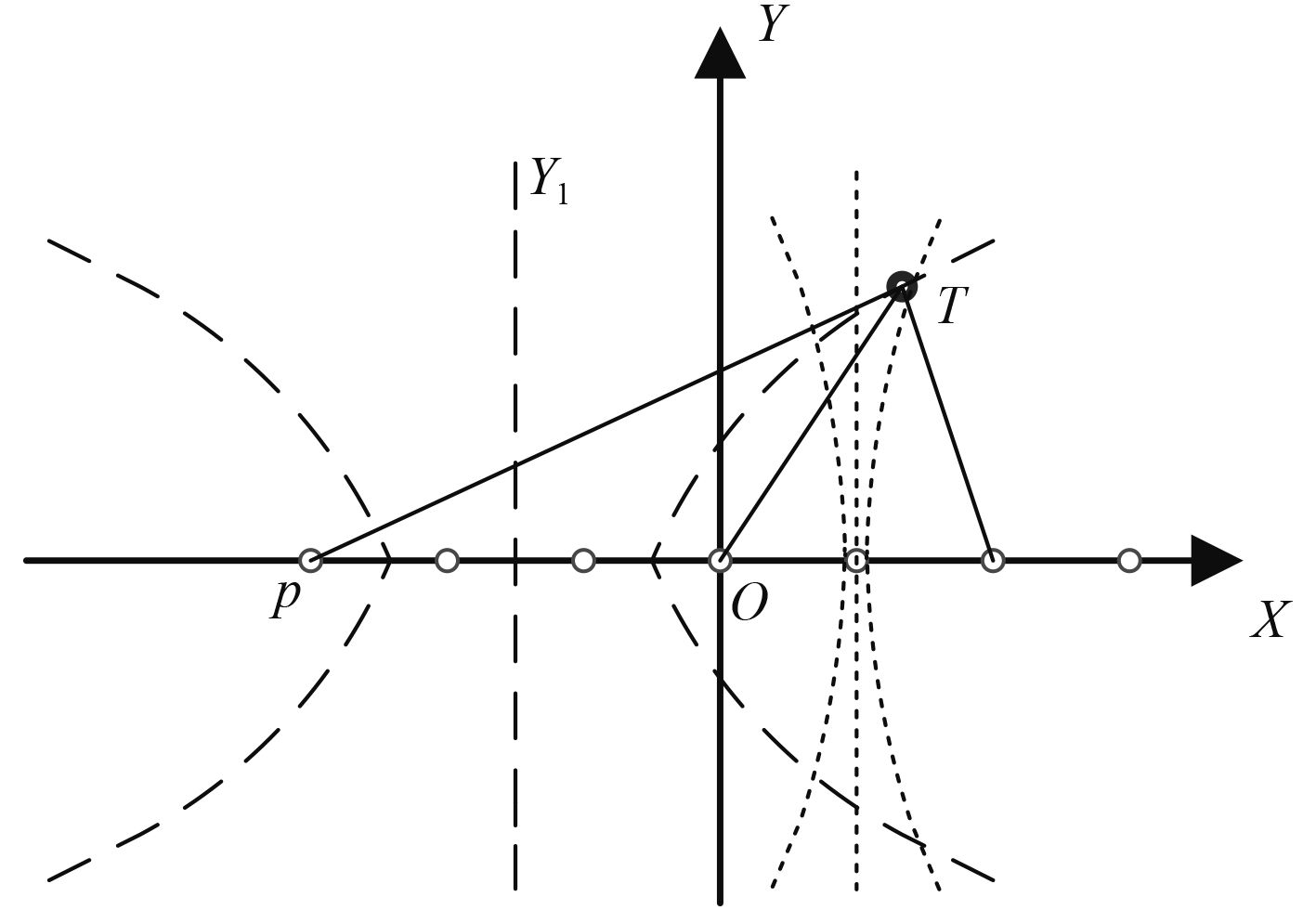
1.1 定位原理线列阵接收阵元沿周向为全向接收,故可视为与水下目标处于同一平面。以线列阵为X轴,中间阵元O为原点建立如图 2所示的平面直角坐标系。
|
图 2 线列阵方位距离估计示意图 Fig. 2 Schematic diagram of towed line array azimuth and distance estimation |
在1个信号周期内,水下目标发射的脉冲到达其它任一选定阵元与中间阵元O的时差可确定1条双曲线轨迹,理论上由2个时差确定的双曲线轨迹交点即为水下目标位置T(x,y)。双曲线方程为:
| $ \left\{ \begin{array}{l} \!\! {x^2}/{a^2} - {y^2}/{b^2} = 1{ \text {,}}\\[5pt] \!\! {c^2} = {a^2} + {b^2}{ \text {。}} \end{array} \right. $ | (1) |
式中:c为任一选定阵元与中间阵元O距离的一半;a为脉冲到达该任一选定阵元与中间阵元O距离差的一半;b为双曲线虚半轴长。
如取P点为选定阵元,其与中间阵元O确定的双曲线中线为Y1,则OP=2c,由双曲线性质可得
| $ \sqrt {{{(x + 2c)}^2} + {y^2}} - \sqrt {{x^2} + {y^2}} = 2a{ \text {,}} $ | (2) |
令
| $ Ra - xc = {c^2} - {a^2}{ \text {。}} $ | (3) |
脉冲到达任一选定阵元与中间阵元O的时差可得到一个具有6个方程的矛盾方程组
| $ \left[ \begin{array}{l} {a_1}\\ {a_2}\\ \vdots \\ {a_6} \end{array} \right.\;\left. \begin{array}{l} {c_1}\\ {c_2}\\ \vdots \\ {c_6} \end{array} \right]\left[ \begin{array}{l} R\\ x \end{array} \right] = \left[ \begin{array}{l} c_1^2 - a_1^2\\ c_2^2 - a_2^2\\ \vdots \\ c_6^2 - a_6^2 \end{array} \right]{ \text {,}} $ | (4) |
解得
系统记录来自线列阵上各个阵元同一脉冲的到达时间TOA(time-of-arrival),并给出相应阵元的序列号。系统已知每个阵元的排列、方向及相应的序列号,可以把TOA数据与阵元在线列阵中的位置结合起来。利用这些数据,针对同一个脉冲建立起TOA/阵元位置数据数组。最后,通过寻找TOA/阵元位置数据数组的最佳拟合曲线,系统计算出发射脉冲的水下目标方位距离的估计值。
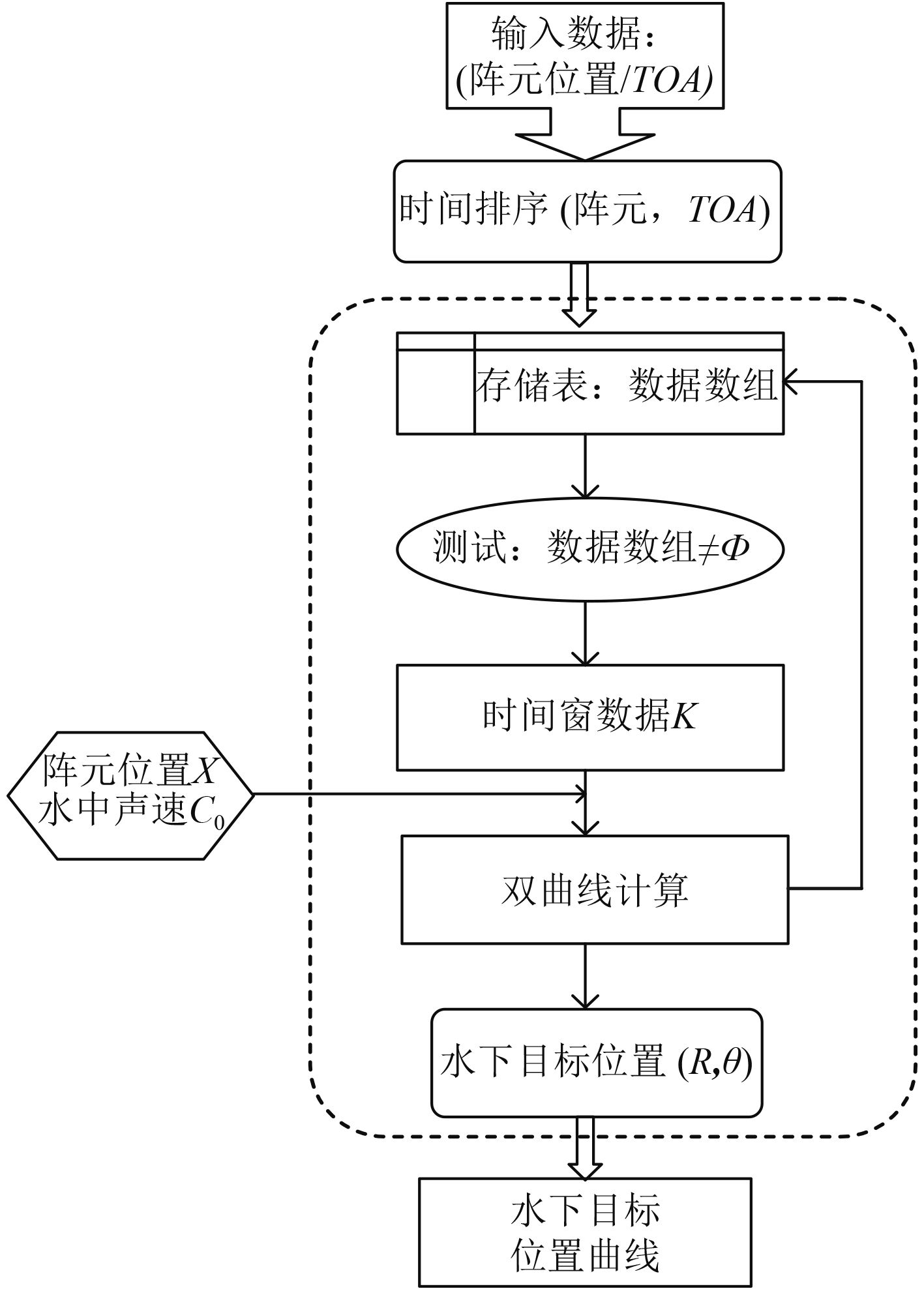
算法描述如下:所有阵元的输入数据保存在1个表中,按时间序列排序。属于各个阵元接收到的同一脉冲数据经由时间窗整理形成数据数组。在每个窗口内计算1次方位/距离估值,随后该数据从表中清除。算法流程如图 3所示。
|
图 3 方位距离估计算法流程图 Fig. 3 Flow chart of azimuth distance estimation algorithm |
1)建立数据数组
如果位于x(i)和x(j)位置的2个阵元i和j接收到同一个脉冲,最大的时差是
| $ 0 < t_j^k - {t_{i0}} < \displaystyle \frac{{\left| {x(i0) - x(j)} \right|}}{{{c_0}}}{ \text {。}} $ | (5) |
这样就产生出1个数据数组
2)单个数据数组的计算
利用由不同阵元检测到的同一个脉冲的TOA和阵元位置序列K,其中包括可能是漏检或错检的数据,要计算出曲线的最佳拟合,来获得水下目标的方位距离信息。在有错误数据存在时,直接运用最小二乘回归算法,会使估算结果严重偏移,因此算法采用最大似然估计,以根据最佳拟合曲线原理求解出的水下目标方位最佳逼近解作为初值,运用迭代加权最小二乘回归方法逼近真值[4],其中权重函数为
| $ w\left( x \right) = \frac{1}{{1 + \frac{{\left| x \right|}}{c}}}{ \text {。}} $ | (6) |
式中:x为阵元实测时差与拟合时差的误差值;c为调谐系数,用于调整x的范围,算法中设为0.1 ms。
迭代计算如下:R0为水下目标距离经典最小二乘近似值,
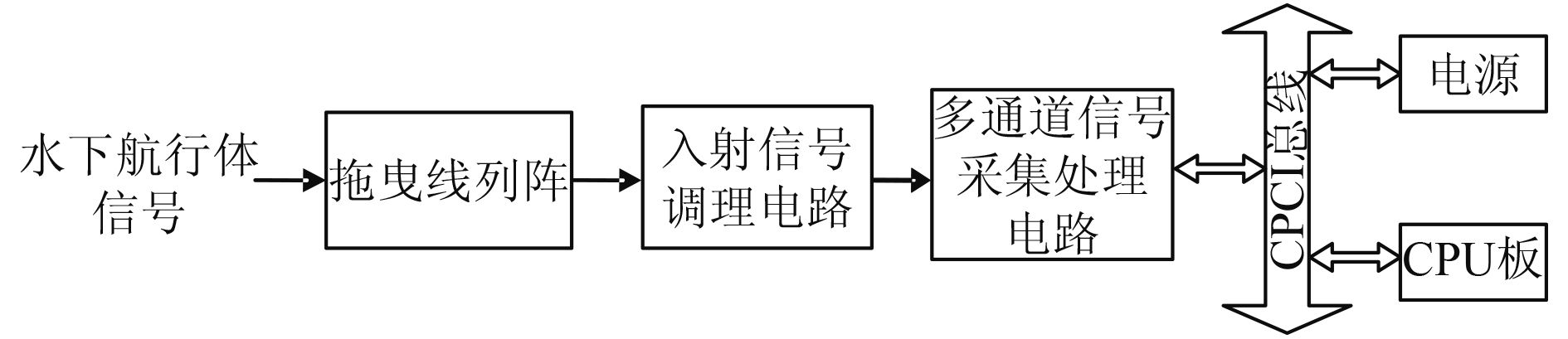
系统利用拖曳线列阵上两两间距为10 m的7个阵元收到的脉冲间到达时差测量水下目标方位距离,系统设备组成如图 4所示。
|
图 4 系统设备组成图 Fig. 4 System equipment composition diagram |
拖曳线列阵多个阵元的接收换能器各自独立工作,当接收到水下目标所发射的声脉冲后,入射信号调理电路对各路脉冲进行放大和滤波调整,使其达到多通道信号采集电路的信号输入要求,信号采集电路对各路输入信号进行采集、预处理和存储,并通过链路口将数据传送到信号处理电路,由其对信号进行分析解算。
2.1 信号处理平台信号处理平台的主控计算机采用CPCI接口单板计算机,使用Windows XP操作系统,它与信号采信处理板上的ADSP-TS101采用CPCI总线进行数据交互,完成信号采集处理板上DSP1程序的加载,并控制相关电路进行工作[5]。除了作为人机交互接口外,主控计算机还为系统提供编程和调试环境。
信号采集处理板主要由输入信号调理电路(输入差分放大器、滤波器、幅度调整电路)、信号采集处理电路、高速数字信号处理芯片ADSP-TS101、CompactPCI总线接口、存储器等构成,其电路框图如图 5所示。
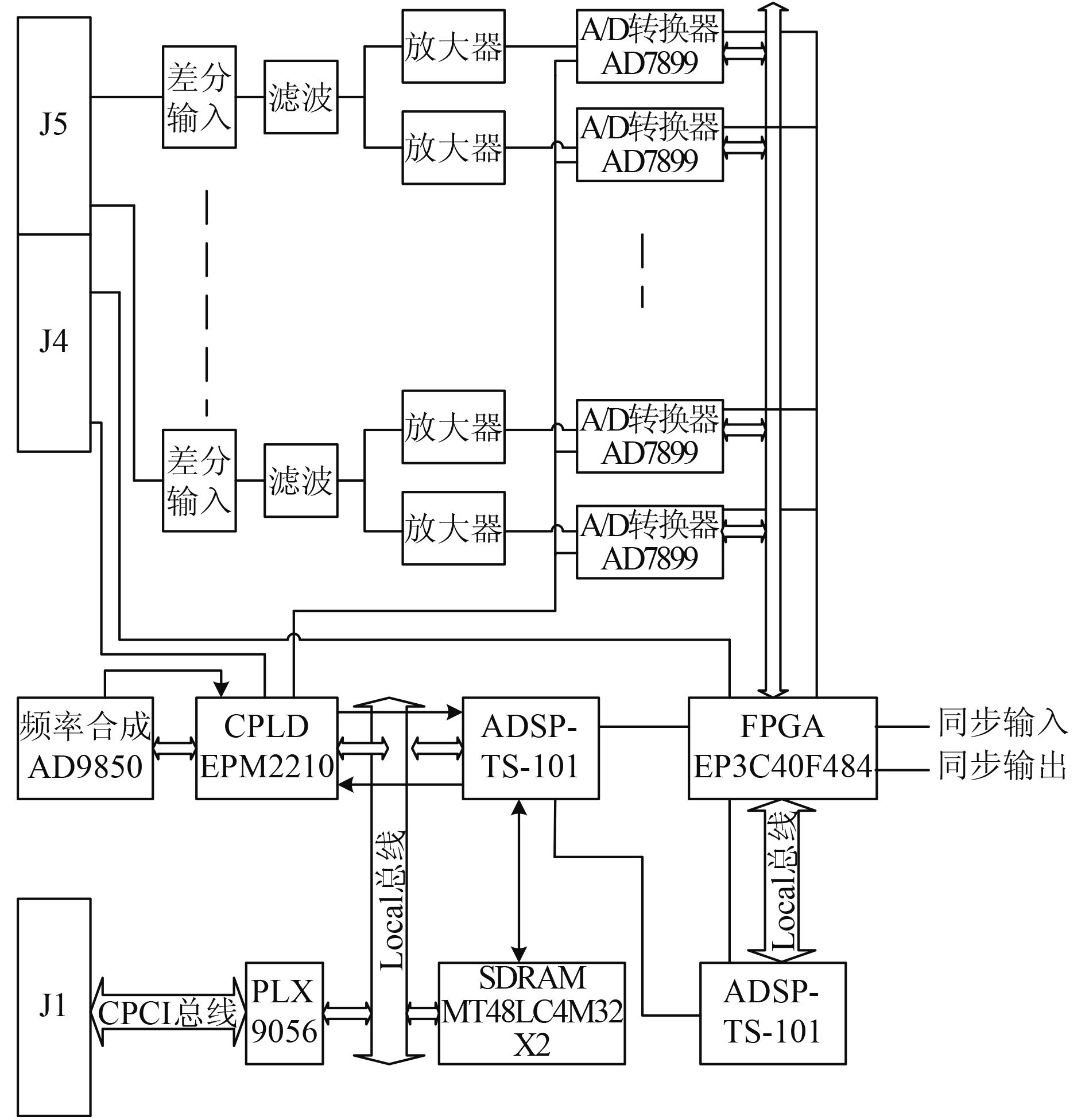
|
图 5 信号采集处理板电路框图 Fig. 5 Block diagram of signal acquisition and processing board |
信号采集电路由7路14位A/D转换器和FPGA构成,A/D转换器采用14-bit的AD7899,最高采样率400 kHz,实际采样率由ADSP-TS101设定,每完成一帧数据采集便向TS101产生中断。各路放大器的增益可控,每通道对应4档增益,增益既可由DSP控制,也可由主控计算机控制。A/D芯片采样时钟由DSP0的串行口产生,芯片的采样数据自动保存在FPGA中,存储器存满后,向DSP0发中断申请,由DSP0把这一块数据读到内部RAM中,对其进行频率均衡等处理后通过链路口送到信号处理电路。
信号处理电路中的DSP1作为中心处理器,通过CPCI总线与主控计算机通讯。A/D采集数据被保存到专门的循环RAM区域中,由DSP1分别进行谱分析检测信号,解算来自线列阵上各个阵元同一脉冲的到达时间,进行目标方位距离估计。
2.2 DSP实现信号处理由1块信号采集处理板完成,采用一主一从共2片DSP的处理结构,每一部分的具体任务如图 6所示。

|
图 6 程序任务分配图 Fig. 6 Program task allocation graph |
2片TS101之间采用链路口连接。1片用作A/D数据采集,以下称为DSP0;另1片用作水下目标信号检测及方位距离解算,称为DSP1。DSP0负责A/D采集及频率均衡处理,DSP1作为中心处理器,进行信号的检测处理工作。DSP0接收AD数据,对A/D数据进行必要的处理后,通过链路口传将数据送到DSP1,或放在DSP1内部存储区,或放在共用外部SDRAM,供DSP1取用,完成信号的检测及位置解算。DSP0除了采集数据的任务外,还可来完成多种数字滤波器的滤波,为后级处理提供信噪比更高的信号。
运行于2片DSP上的程序分别编写,DSP0程序编译为.ldr格式,在DSP1程序编译时嵌入,当DSP1程序加载运行后,通过链路口加载DSP0程序。DSP0程序自动引导运行后使能其链路口中断,等待DSP1发送FIR滤波器参数,接收完毕后使能IRQ中断,读取A/D芯片的采样数据并进行FIR滤波,通过链路口将均衡处理后的数据送向DSP1。DSP1接收A/D数据,分别作FFT,计算频率、脉宽、幅度、周期、信噪比等,检测有效信号,确定脉冲到达各阵元的时间,解算水下目标方位距离。
程序将原始输入数据、检测估算结果、有参考价值的中间结果都以循环数据区的方式保存,只要保证存储区域足够长,主控计算机程序就可以按照允许一定误差的时间间隔,读取ADSP-TS101的内部存储器,供主控计算机实时显示和保存。
程序工作流程如图 7所示。
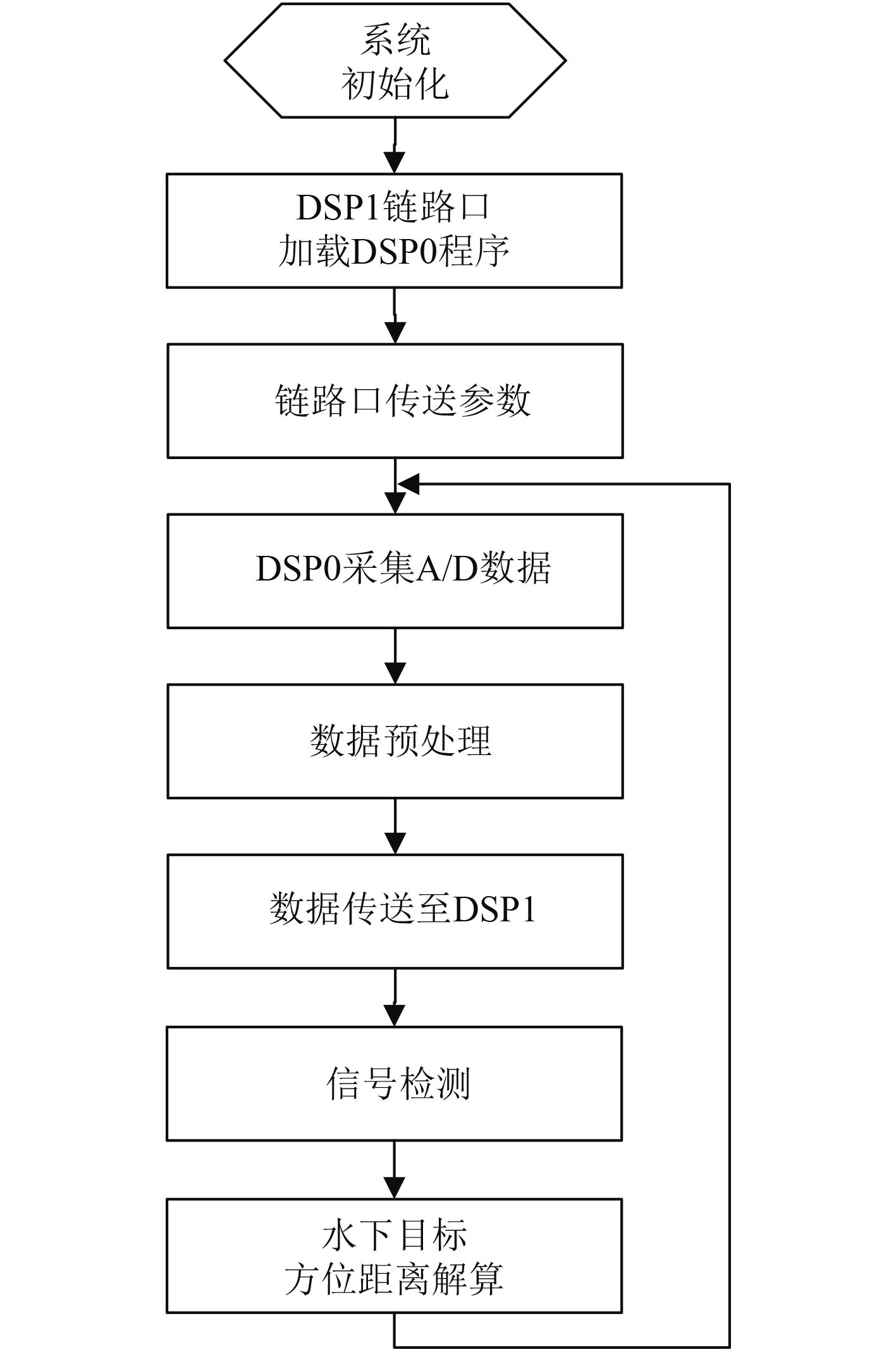
|
图 7 程序工作流程图 Fig. 7 Process flow chart |
DSP程序负责对线列阵多个阵元接收到的水声信号进行检测处理,识别水下目标发射信号并计算其到达不同阵元的时刻,结合各阵元已知位置,解算水下目标方位距离值。程序在Windows操作系统下,由VisualDSP++ 4.5开发环境编写,采取集成化、模块化设计,各项独立功能均单独形成模块,便于调试和使用[6]。
线列阵水下目标方位距离估计程序由以下6个模块构成:
1)链路口加载模块。主要功能是结合主机引导方式,通过链路口对信号采集处理电路中DSP0发送加载码和用户程序,完成多DSP的程序加载。
2)A/D采集模块。主要功能是在每个中断周期中读取A/D芯片采集的多路数据,送至DSP0内部存储区中。
3)频率均衡模块。主要功能是设计任意响应的数字滤波器,滤除带外信号,修正由于各种原因引起的信号输入不均衡。
4)信号检测模块。主要功能是对数据块作加窗处理后进行频谱分析[7],计算该块数据的频率、电压幅度、信噪比等,检测水下目标发射信号到达线列阵各阵元时刻。
5)参数接收发送模块。主要功能是在主片DSP1和从片DSP0之间通过链路口通信,传送参数和数据。
6)方位距离解算模块。主要功能是使用时差数据和线列阵阵元位置数据,解算水下目标方位距离信息,并进行误差修正。
3 测试及分析完成实验室验证后,在湖上对系统进行静态测试,测试结果如图 8和表 1所示。
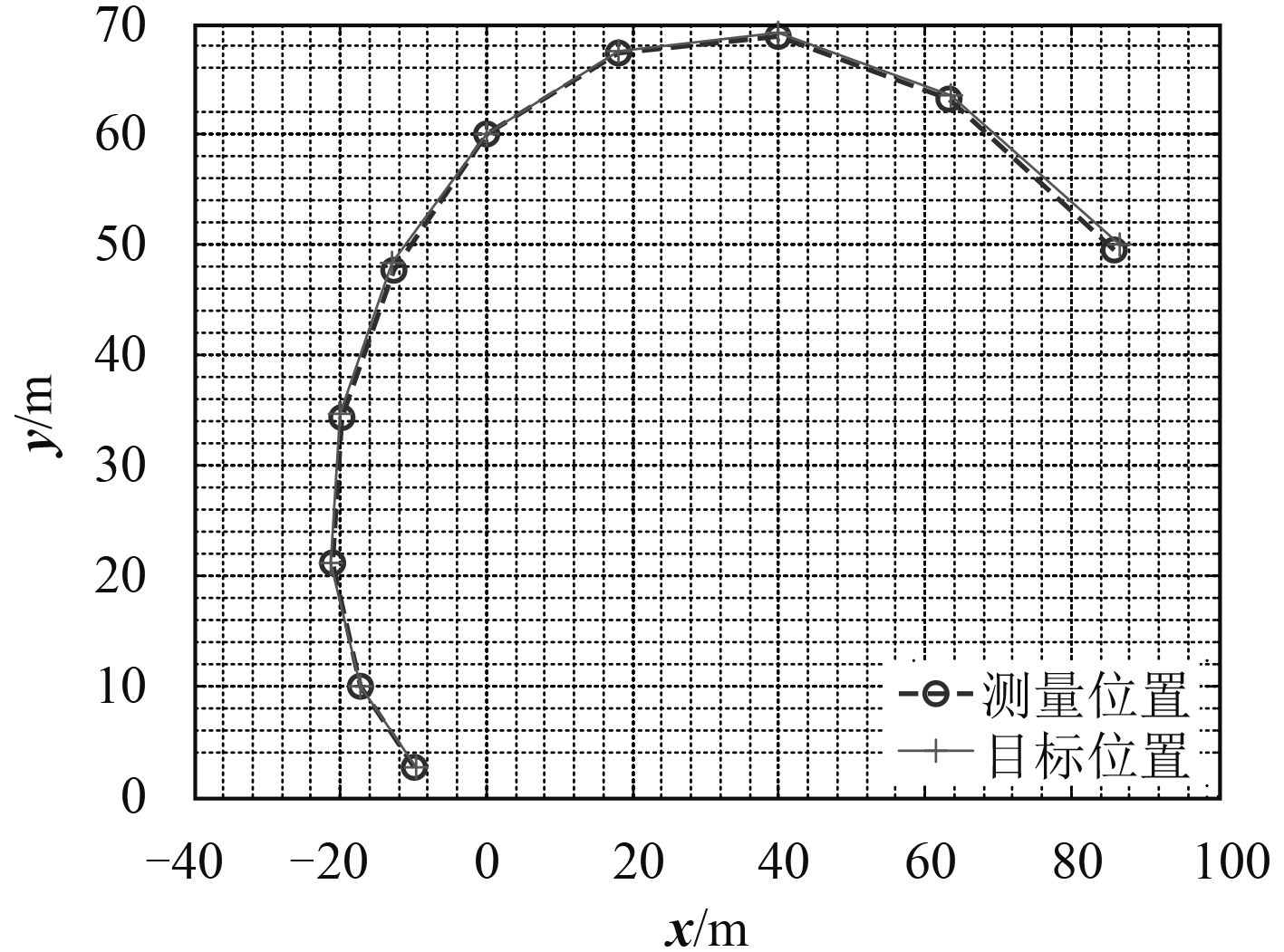
|
图 8 水下目标位置对照图 Fig. 8 Underwater target position contrast figure |
|
|
表 1 方位距离解算对照表 Tab.1 Azimuth distance solution contrast table |
在测试过程中发现,在一定误差范围内,阵元定位误差对水下目标方位距离的估计结果影响较小,相对而言,脉冲到达时间误差对估计结果影响较大,水下待测目标的声源信号信噪比较高时可得到较为准确的时延估计值。因此,在实际程序设计中,应该尽量提高对水下目标发射脉冲的检测准确性,提高对其到达阵元时间测定的精确度。另外,算法对水下目标方位角度估计的准确性相当高,且对阵元定位误差和脉冲到达时间误差的容错性较好,这也是水下多种定位算法的通常特性。
4 结语本文主要介绍了线列阵水下目标方位距离估计算法在ADSP数字信号处理平台上的实现,描述了算法原理和实现方法,并详细介绍了DSP程序开发的过程,最后进行了湖上静态测试,结果表明,算法的设计符合原理,程序实现满足系统需要,可以基本准确估计水下目标方位距离。
| [1] | 安良, 张学峰, 陈励军, 等. 柔性阵被动定位系统中的阵形测量与互相关峰跟踪算法研究[J]. 声学技术 , 2011, 30 (3):210–212. |
| [2] |
安良, 陈励军, 陆佶人, 等. 船载柔性阵基元坐标实时获取技术研究[J]. 数据采集与处理 , 2010, 25 (1):86–92.
AN Liang, CHEN Li-jun, LU Ji-ren, et al. Element coordinate measurement of ship-based flexible hydrophone array[J]. Journal of Data Acquisition & Processing , 2010, 25 (1) :86–92. |
| [3] | 田坦, 刘国枝, 孙大军. 声呐技术[M]. 哈尔滨: 哈尔滨工程大学出版社, 2000: 247-248. |
| [4] | 毛卫宁. 水下被动定位方法回顾与展望[J]. 东南大学学报(自然科学版) , 2001, 31 (6):129–132. |
| [5] | 刘书明, 苏涛, 罗军辉. TigerSHARC DSP应用系统设计[M]. 北京: 电子工业出版社, 2004: 134-135. |
| [6] | Analog Devices公司. TigerSHARC DSP硬件指南Part # ADSP-TS101S[EB/OL]. United States:Analog Devices公司, 2002:16-19. |
| [7] | 胡广书. 数字信号处理-理论、算法及实现[M]. 北京: 清华大学出版社, 2003: 304-305. |
 2016, Vol. 38
2016, Vol. 38
