目标到达方向(DOA)的估计问题是一个经久不衰的课题,它在雷达、声呐、无线通信等领域中都有广泛的应用。到目前为止,大量的阵列设计和信号处理方法可以用来实现不同情况下的DOA估计[1-2],本文将主要讨论的阵元分布,对DOA的估计性能有着至关重要的影响,它主要包括阵元数量和位置参数。
实际情况中,目标在某些方位范围内出现的概率较高,这些先验知识可以用来指导阵列设计,优化DOA的估计性能。本文提出一种最优阵列设计方法,在DOA是一个已知概率密度的随机变量前提下,在指定布阵区域内确定最优阵元分布方案,实现最佳DOA估计性能。本文主要讨论平面阵对方位角的估计问题,方法可以推广到立体阵对方位角和俯仰角的估计。
1 系统建模假设在二维平面
| $\boldsymbol{r}=\left[ {{\boldsymbol{r}}_{1}},{{\boldsymbol{r}}_{2}},...,{{\boldsymbol{r}}_{N}} \right]=\left[ \begin{matrix} {{x}_{1}} & {{x}_{2}} & ... & {{x}_{N}} \\ {{y}_{1}} & {{y}_{2}} & ... & {{y}_{N}} \\ \end{matrix} \right]\text{,}$ | (1) |
目标与阵列在同一个平面内,信号s(t)从方位θ入射,则K个快拍的接收数据可以表示为:
| $\boldsymbol{x}(t)={{\boldsymbol{A}}_{\theta }}(t)\boldsymbol{s}(t)+\boldsymbol{n}(t)\begin{matrix} {} & t=1,2,...,K \\ \end{matrix}\text{,}$ | (2) |
式中: x (t)为接收数据矩阵; n (t)为噪声矩阵;驾驶向量:
| ${{\boldsymbol{A}}_{\theta }}={{\left[ {{\rm e}^{{\rm j}2\text{ }\!\!\pi\!\!\text{ } f{{\tau }_{1}}\left( \theta \right)}},{{\rm e}^{j2\text{ }\!\!\pi\!\!\text{ } f{{\tau }_{2}}\left( \theta \right)}},...,{{\rm e}^{{\rm j}2\text{ }\!\!\pi\!\!\text{ } f{{\tau }_{N}}\left( \theta \right)}} \right]}^{\rm T}}\text{。}$ | (3) |
式中:
本文中阵元分布(r
的选取)目的在于实现最优的目标DOA估计。假定阵元被约束在由封闭曲线
在第1节模型的基础上,由接收数据
| $FIM(\boldsymbol{r},\theta )=G(\boldsymbol{r},\theta )\cdot P\text{,}$ | (4) |
| $G(\boldsymbol{r},\theta )=\frac{du{{(\theta )}^{T}}}{{\rm d}\theta }B\frac{du(\theta )}{{\rm d}\theta }\text{,}$ | (5) |
| $B=\frac{1}{N}(\boldsymbol{r}-{{\boldsymbol{r}}_{A}}){{(\boldsymbol{r}-{{\boldsymbol{r}}_{A}})}^{\rm T}}\text{。}$ | (6) |
由式(4)可看出FIM由2项的乘积构成,第1项
克拉米罗下限(CRLB)是式(4)费舍尔信息矩阵的倒数,即
定义CRLB最佳阵设计准则,阵元分布
| ${{\boldsymbol{r}}_{C}}=\arg \underset{\boldsymbol{r}\in D}{\mathop{\min }}\,{{J}_{C}}(\boldsymbol{r})\text{,}$ | (7) |
其中CRLB代价函数
| $\begin{align} & {{J}_{C}}(\boldsymbol{r})={{E}_{\theta }}\{{\rm {CRLB}}(\boldsymbol{r},\theta )\}=\int_{-\text{ }\!\!\pi\!\!\text{ } }^{\text{ }\!\!\pi\!\!\text{ } }{{\rm {CRLB}}(\boldsymbol{r},\theta )}f(\theta ){\rm d}\theta = \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \int_{-\text{ }\!\!\pi\!\!\text{ } }^{\text{ }\!\!\pi\!\!\text{ } }{\frac{1}{FIM(\boldsymbol{r},\theta )}}f(\theta ){\rm d}\theta\text{。} \\ \end{align}$ | (8) |
其中
空间方位波束宽度可以定量的衡量波束形成对目标DOA的分辨能力。考虑到波束形成是驾驶向量和接收数据的点乘求和累积运算,假设目标DOA为
| $\begin{split} {{W}_{{{\theta }_{0}}}}(\theta )={{a}^{H}}(\theta )a({{\theta }_{0}})\text{,}a(\theta )=\quad \quad \quad \quad \quad \quad\quad \quad \quad\\ \!\!\!\!\!\!\!\! {{\left[ {{\rm e}^{{j2\text{ }\!\!\pi\!\!\text{ } {{f}_{0}}(u{{(\theta )}^{\rm T}}\cdot {{\boldsymbol{r}}_{1}})}/{c}}},{{\rm e}^{{j2\text{ }\!\!\pi\!\!\text{ } {{f}_{0}}(u{{(\theta )}^{\rm T}}\cdot {{\boldsymbol{r}}_{2}})}/{c}}},...,{{\rm e}^{{j2\text{ }\!\!\pi\!\!\text{ } {{f}_{0}}(u{{(\theta )}^{\rm T}}\cdot {{\boldsymbol{r}}_{N}})}/{c}}} \right]}^{\rm T}}\text{。}\!\!\! \end{split}$ | (9) |
其中H为取共轭转置。阵增益
| $\left| {{W}_{{{\theta }_{0}}}}(\theta ) \right|\approx N-\frac{N}{2}{{\left( \frac{2\pi }{{{\lambda }_{0}}} \right)}^{2}}G\left( \bf{r},{{\theta }_{0}} \right){{\left( \theta -{{\theta }_{0}} \right)}^{2}}\text{。}$ | (10) |
令式(10)中
根据以上推导结果,可以更直观地分析目标DOA估计性能与目标方位
仿真所选择的信号频率均满足半波长布阵条件:
受约束的封闭曲线
假定目标DOA概率密度函数为
| $ \left\{ \begin{align} & {{\theta }_{1}}=-{{{\theta }_{0}}}/{2}\; \\ & {{\theta }_{2}}={{{\theta }_{0}}}/{2}\; \\ \end{align} \right.,\ \ \ \left( {{\theta }_{0}}={{\theta }_{2}}-{{\theta }_{1}} \right)\text{。} $ |
为了方便理解和观察,先介绍三元阵仿真实验,然后进行多元阵仿真分析(注意:下文将会出现两类关于角度的表述,一类为目标入射角度,另一类为阵元在圆环上的方位分布,须注意区分)。
3.1 三元阵仿真仿真实验中,选择具有代表性的DOA概率分布
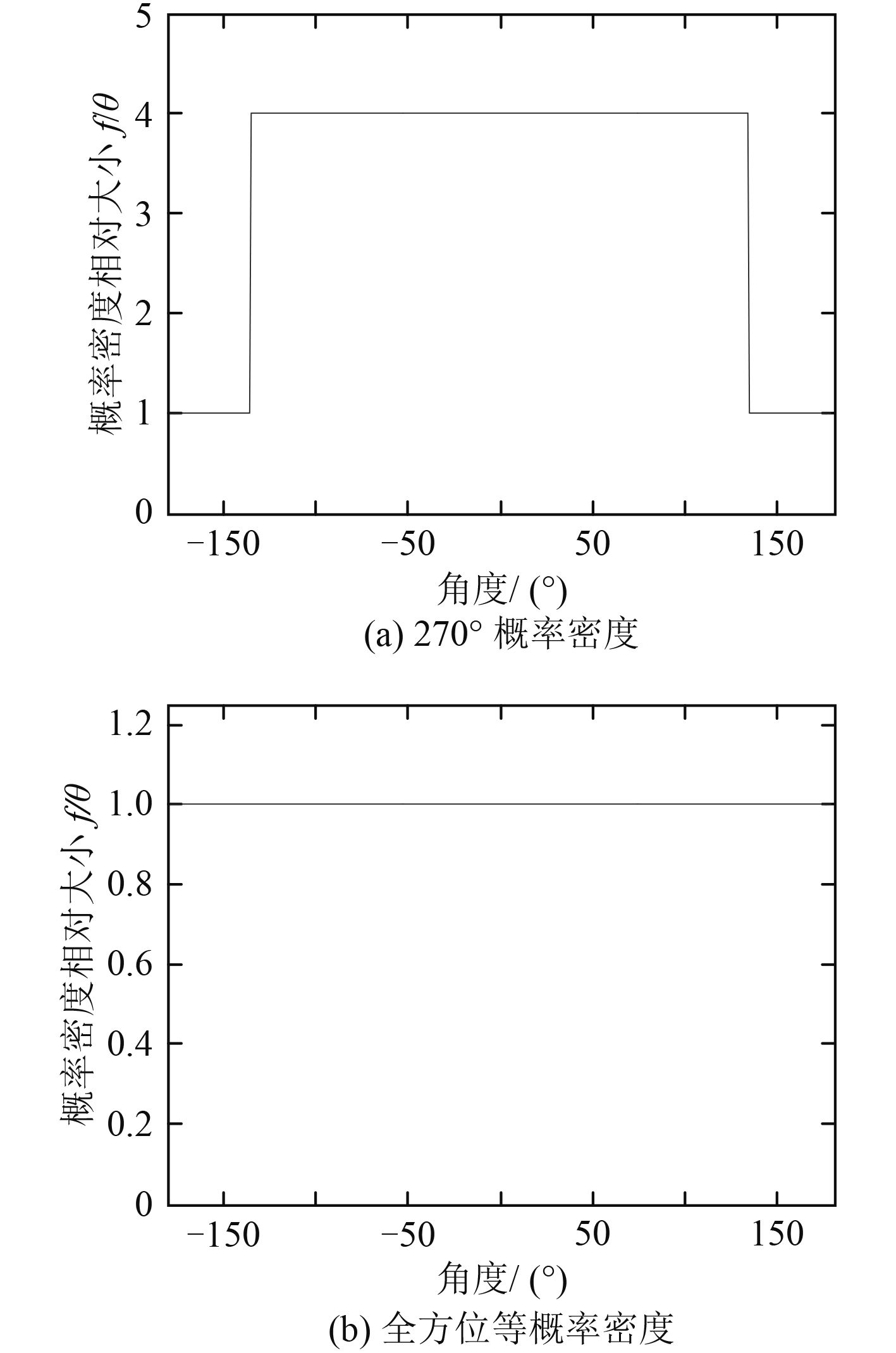
|
图 1 DOA概率密度分布 |
为了方便表述,将3个阵元分别编号:1#、2#和3#。
当270°高概率入射时,根据CRLB准则,由式(7)和式(8)计算得到3个阵元在圆环上的位置分布,如图 2所示,分别位于0°,-125°和125°。图 3给出了1#阵元固定位置0°时,代价函数Jc(r )随2#和3#阵元位置的变化情况,浅色*处取到最小值,分别对应-125°和125°。
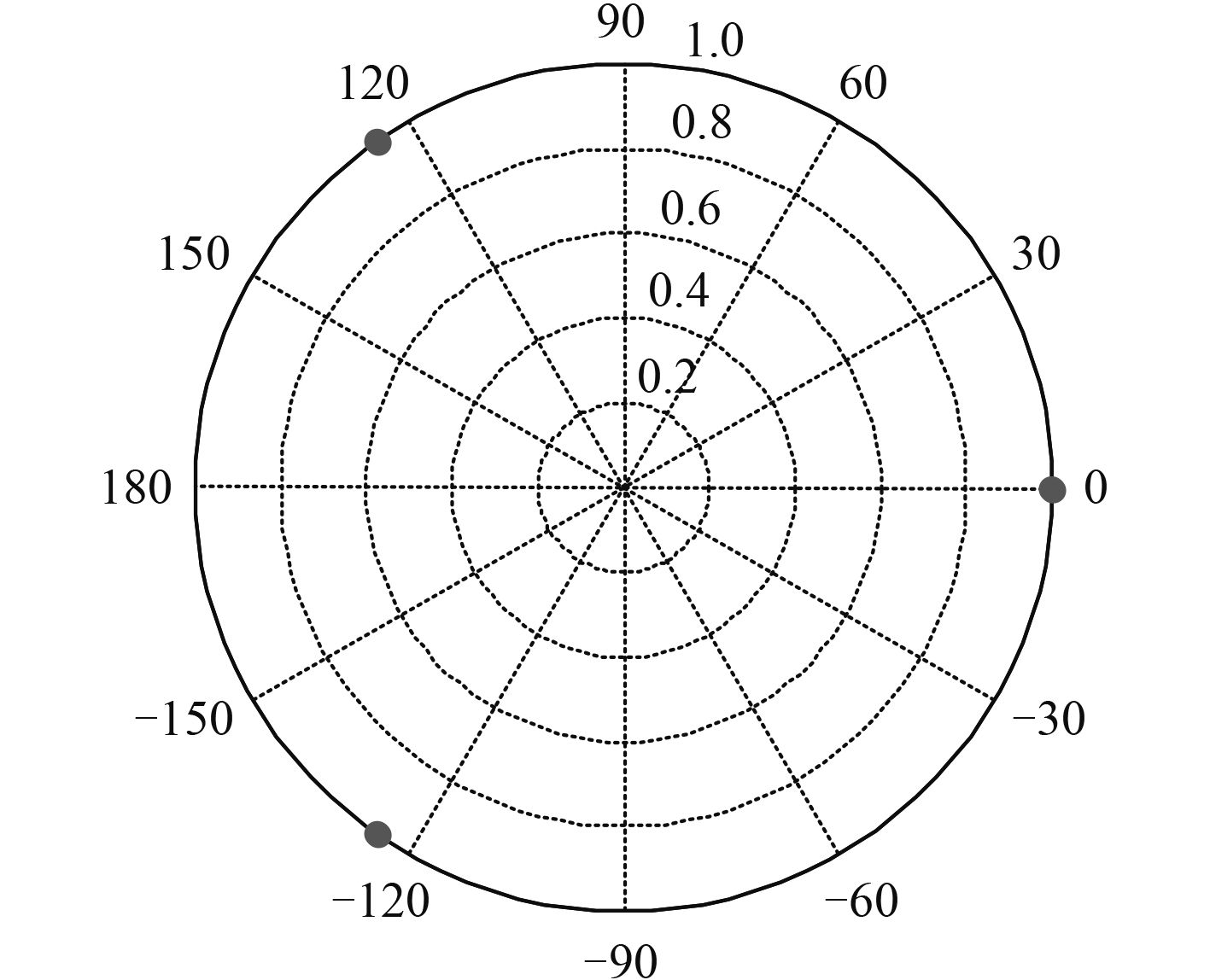
|
图 2 阵元分布 |
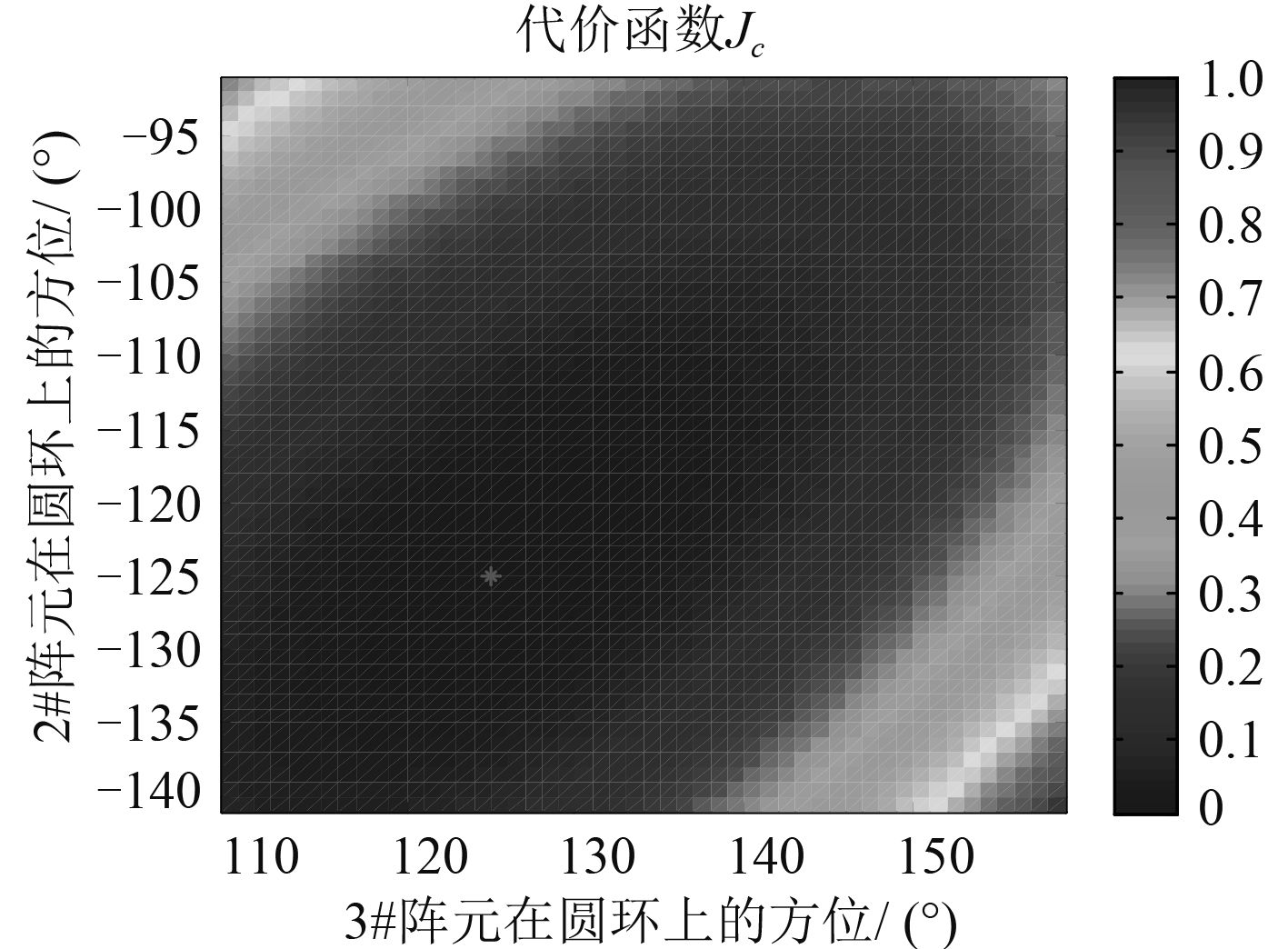
|
图 3 Jc(r)随2#和3#阵元位置变化情况 |
当360°高概率入射时,即各向同性概率入射的情况下(对目标完全没有先验知识的情况亦可归为此类),1#,2#和3#阵元分别在圆环的0°,-120°和120°方位可使Jc(r )取到最小值,阵元分布如图 4所示。
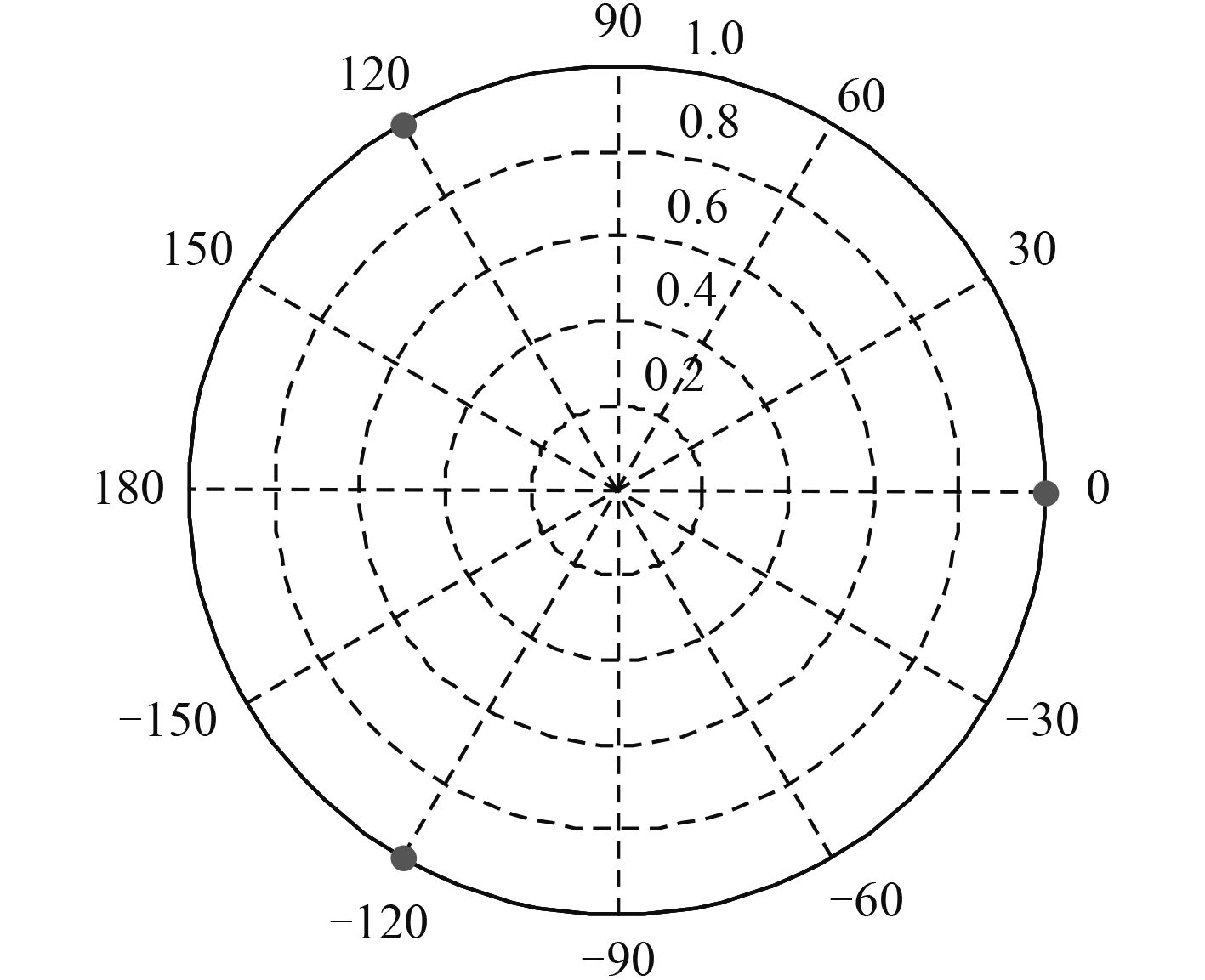
|
图 4 阵元分布 |
可见,在未知入射方位概率密度情况下,阵元在圆环上均匀分布的方案是符合CLRB准则的最佳布阵方式。
图 5给出了三元阵在0°~360°高概率密度入射情况下的阵元分布规律。
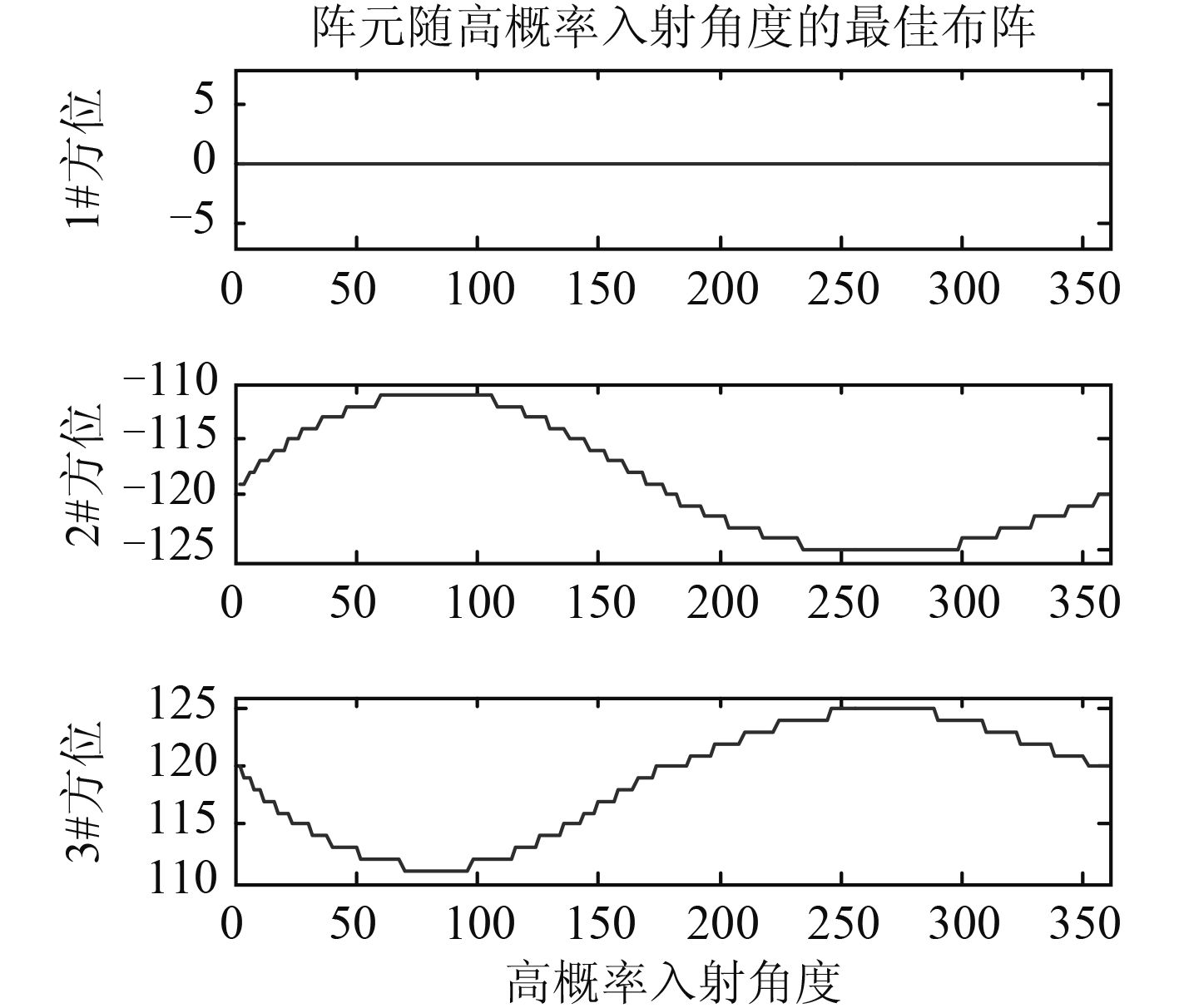
|
图 5 随DOA入射概率的阵元分布 |
逐渐增加圆环阵的阵元个数,本小节采用五元阵和七元阵进行仿真实验。基于CRLB准则,在140°高概率入射情况下(见图 6),由式(7)和式(8)直接计算得到阵元分布情况。
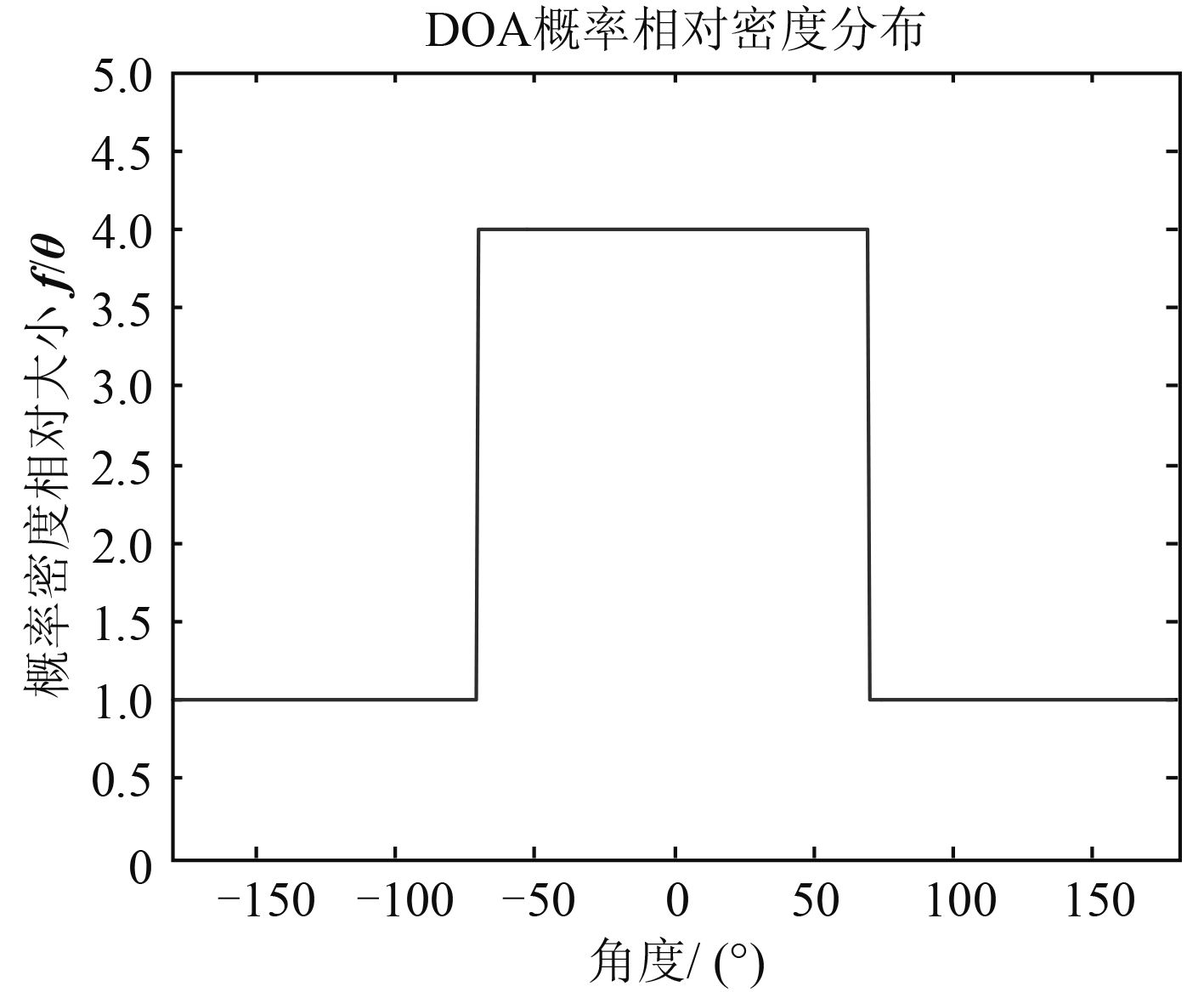
|
图 6 140°高概率密度函数 |
五元阵1#~5#阵元在圆环上对应方位分别为0°,-77°,77°,-135°,135°,它与等间距布阵的五元阵对0度方向入射信号的常规平面波波束形成对比结果如图 7所示。
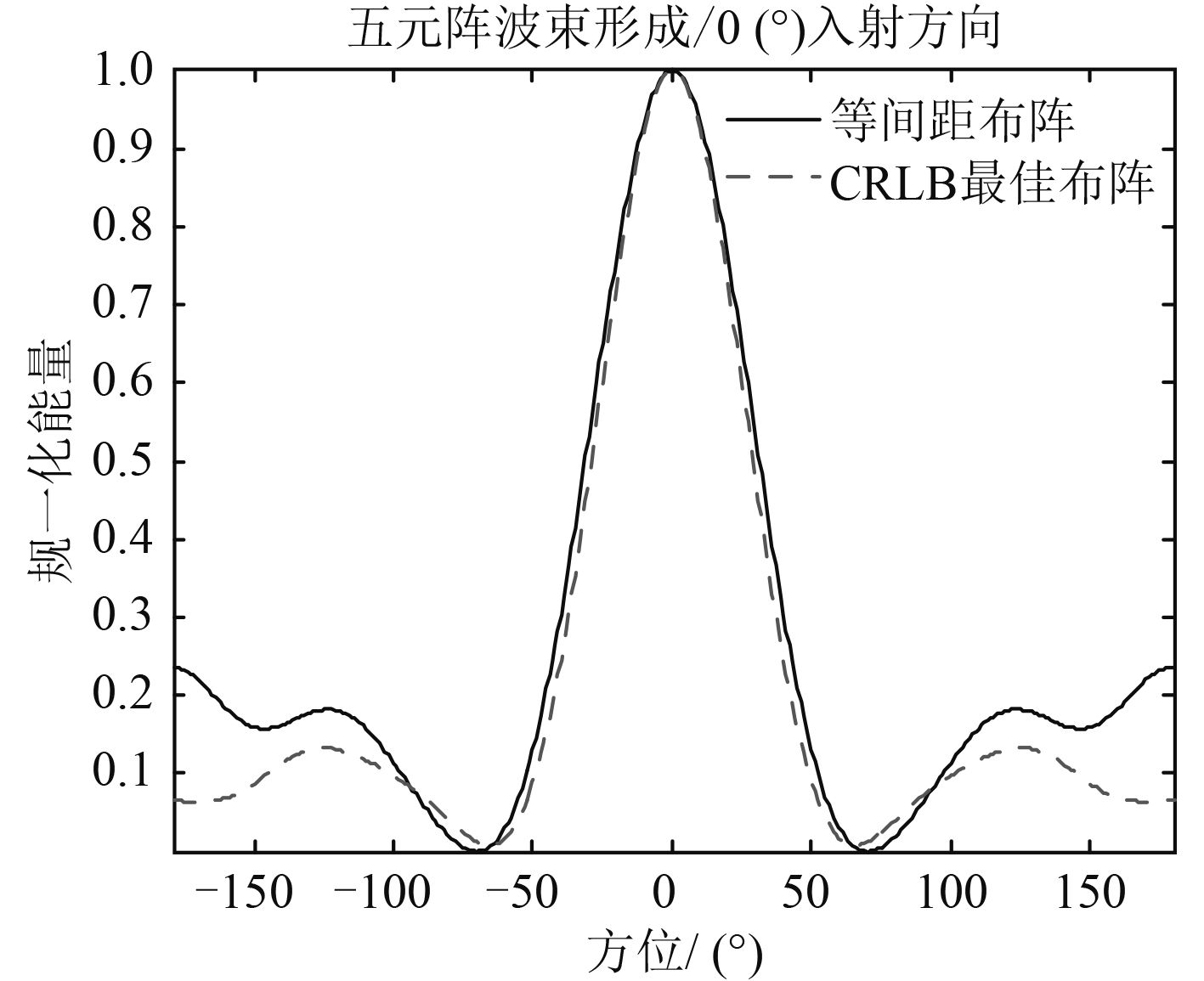
|
图 7 五元阵波束形成对比 |
七元阵1#~7#阵元在圆环上对应方位分别为0°,-60°,60°,-95°,95°,-145°,145°,它与等间距布阵的七元阵对0度方向入射信号的常规平面波波束形成对比结果如图 8所示。
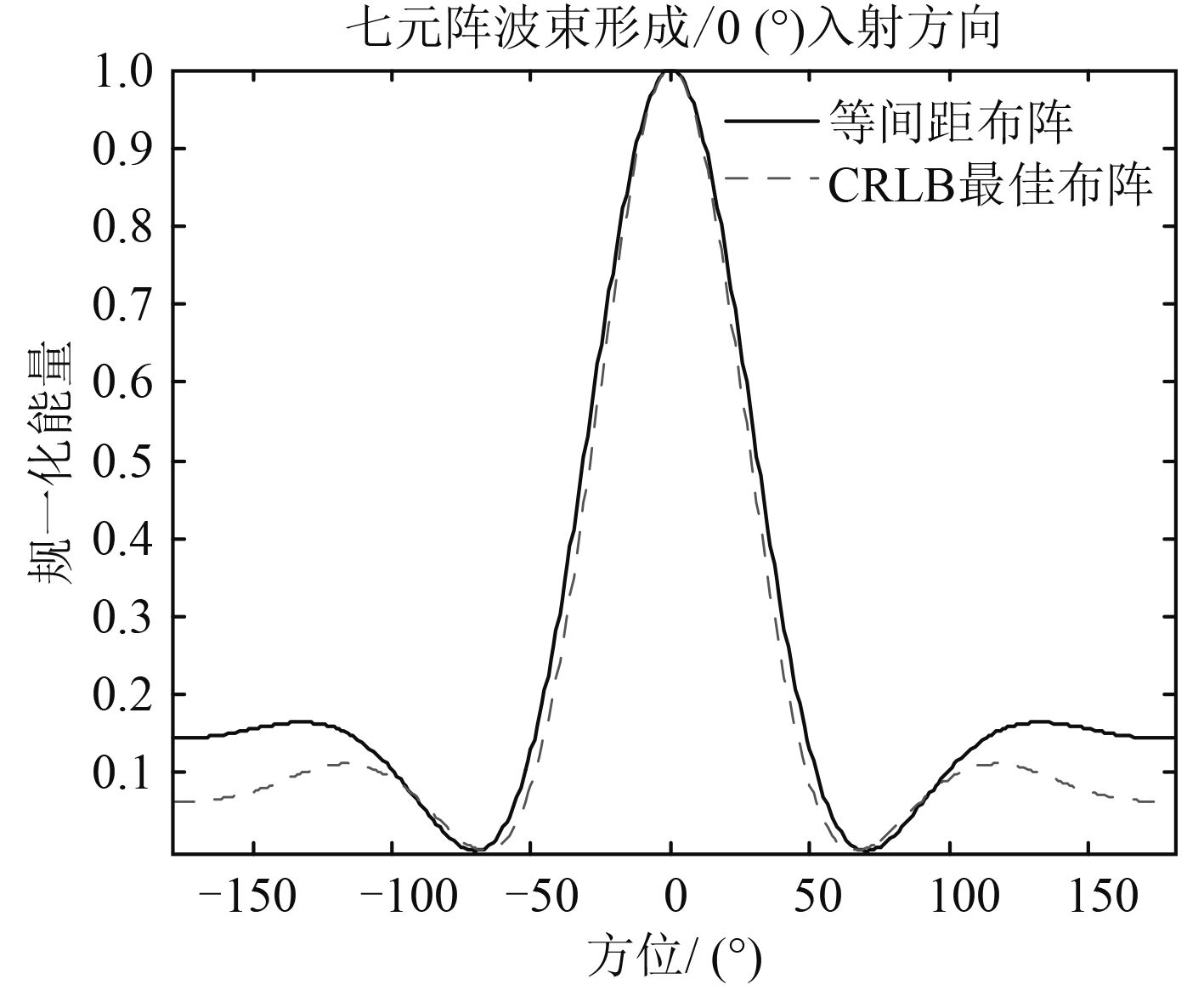
|
图 8 七元阵波束形成对比 |
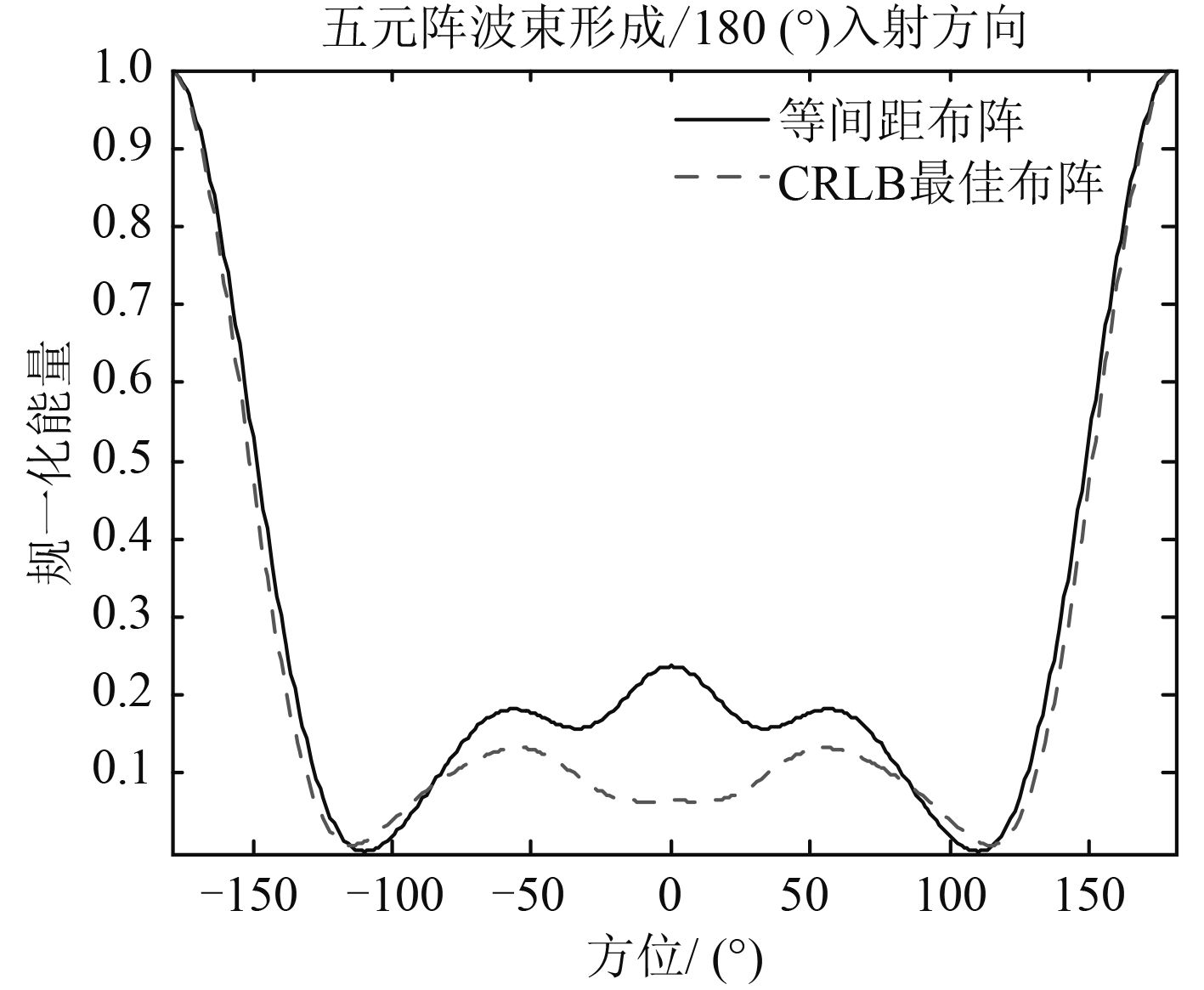
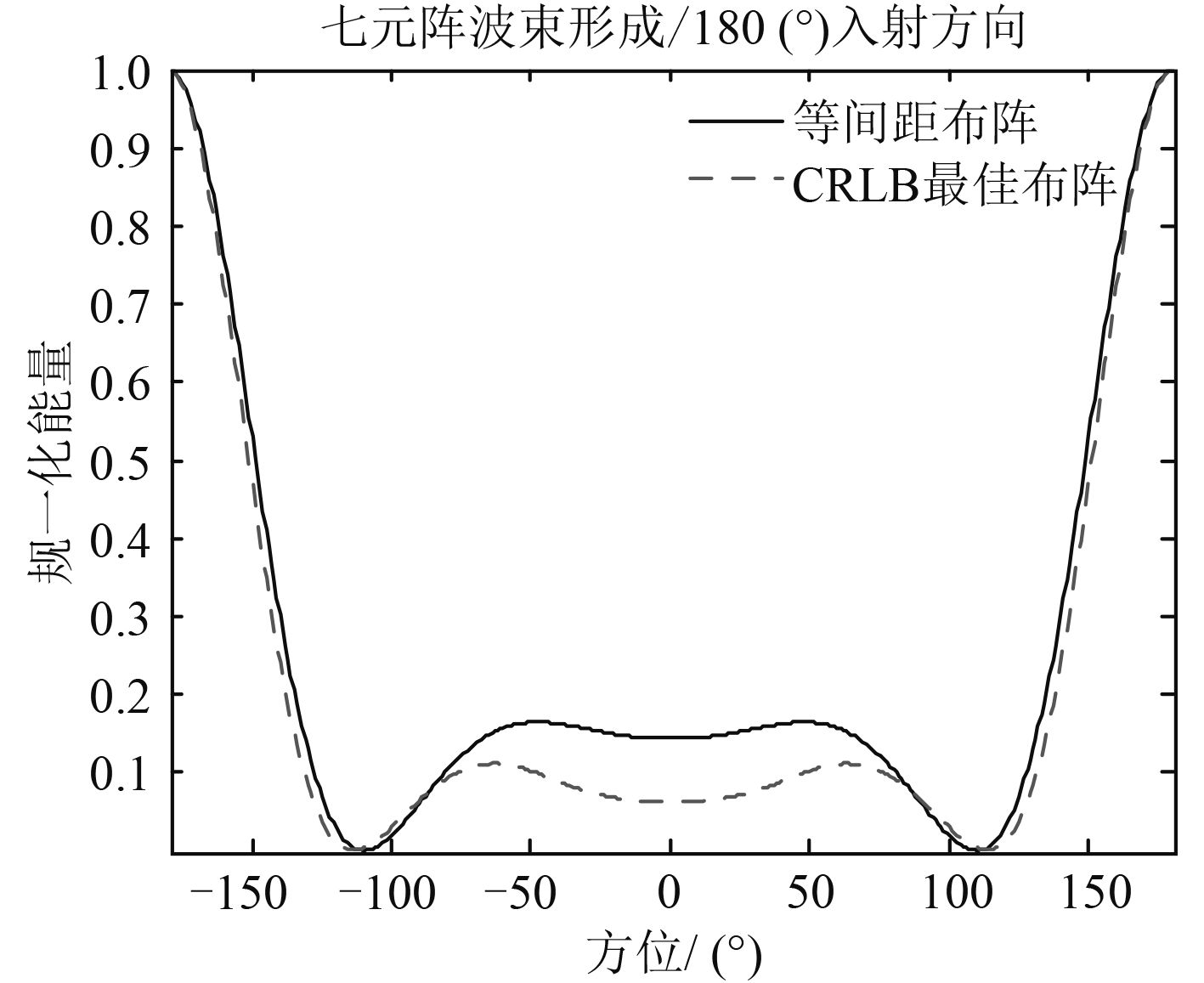
从图 7的五元阵和图 8的七元阵波束形成结果可以看到,CRLB准则下的最佳布阵相比于等间距布阵,实现了高可靠分辨。同时,此方法设计的阵列,阵元关于0°和180°所在直线成轴对称分布,这使得波束形成在180°附近同样具有高可靠分辨能力,如图 9和图 10。
|
图 9 五元阵波束形成对比 |
|
图 10 七元阵波束形成对比 |
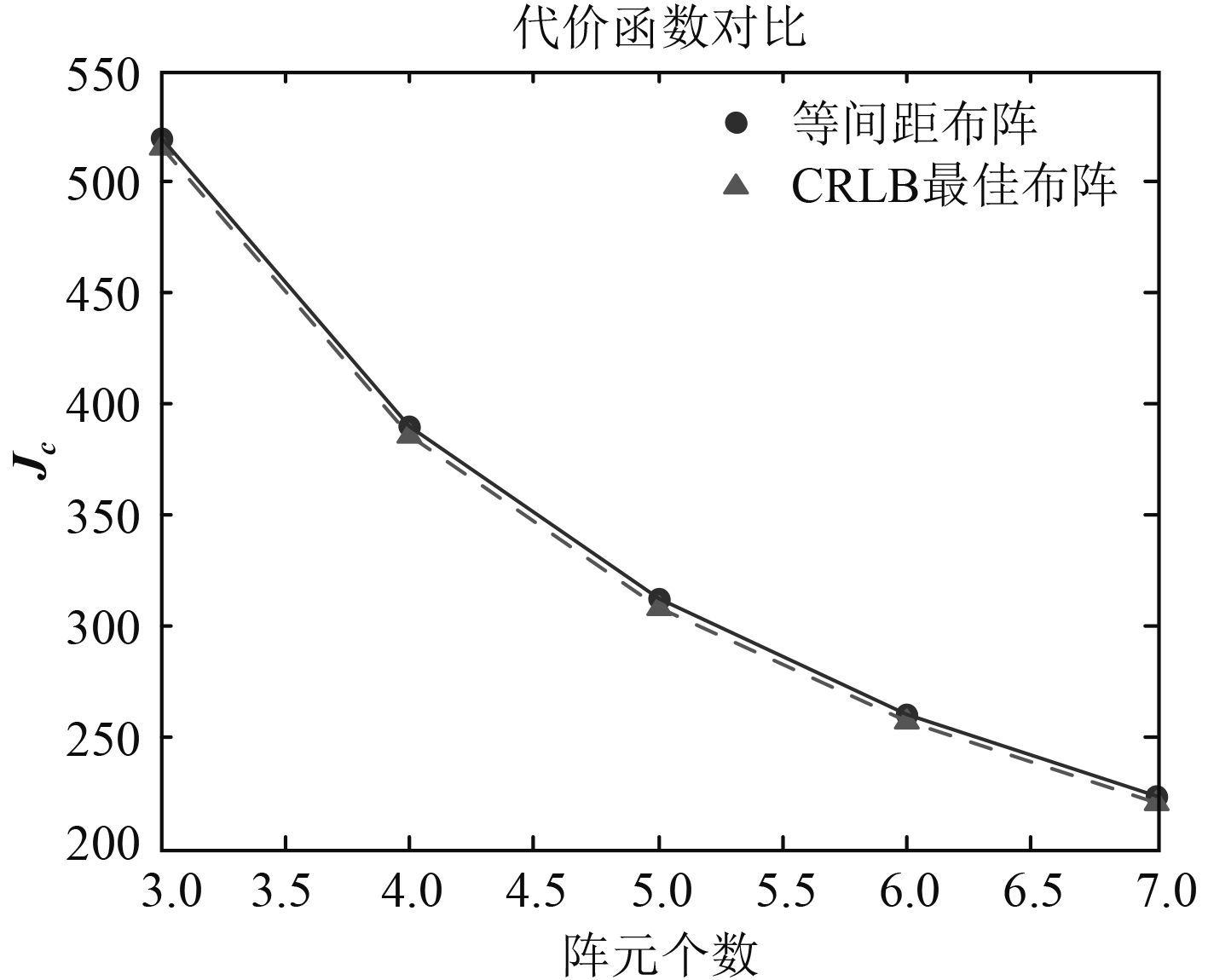
图 11给出了三、四、五、六、七元阵在[-70°70°]高概率入射情况下,目标从0°方向入射时的等间距布阵和CRLB最佳布阵的代价函数
|
图 11 CRLB最佳布阵和等间距布阵的代价函数 |
根据第2.2节的公式推导分析,CRLB最佳阵设计准则实现了最小平均波束宽度,在某些感兴趣的信号入射角度区间内具有较窄的主瓣宽度。从图 7的五元阵和图 8的七元阵波束形成仿真结果可看到,已知目标DOA的概率分布情况,CRLB准则下的最佳布阵相比于等间距布阵,具有旁瓣低且主瓣窄的优势,实现了高可靠分辨。
4 结语本文提出了一种在边界受约束情况下的基于CRLB准则的新型布阵方案。当具备目标入射角度先验知识(主要指目标入射角度的概率密度函数)时,解析表达式(7)和式(8)可以直接代入求解,得到各个阵元的布阵位置。
通过对三元、五元、七元阵设计的仿真实验,根据本文所提出的算法,得到的布阵方案明显地提高了阵列信号处理在方位估计性能方面的可靠性和分辨力。同时,该方法可以推广到空间三维布阵,得到目标入射方向的方位角和俯仰角的最佳估计。
随着阵元个数增多,会出现维度过高,计算量过大的问题,为解决此问题可以采取分级处理,先将边界划分为多个子区域,对每个子区域做CRLB最佳布阵,可以得到次最佳效果,具体方法将在后续论文中进行描述。
| [1] | VAN TREES H L. Optimum array processing[M]. New York: Wiley, 2002. |
| [2] | MACDONALD V H. Optimum bearing estimation with passive sonar system[D]. New Haven:Yale University, 1971. |
| [3] | WEISS A J, FRIEDLANDER B. On the Cramer-Rao bound for direction finding of correlated signals[J]. IEEE Transactions on Signal Processing , 1993, 41 (1) :495–499. |
| [4] | DORON M A, DORON E. Wavefield modeling and array processing. III. Resolution capacity[J]. IEEE Transactions on Signal Processing , 1994, 42 (10) :2571–2580. DOI: 10.1109/78.324724 |
| [5] | BAYSAL U, MOSES R L. On the geometry of isotropic arrays[J]. IEEE Transactions on Signal Processing , 2003, 51 (6) :1469–1478. DOI: 10.1109/TSP.2003.811227 |
 2016, Vol. 38
2016, Vol. 38
