0 引言

水下目标识别一直是国内外水声学者研究的热点和难点技术之一。近年来随着减震降噪技术的发展，运动目标在高频段辐射的噪声大大减小，这为被动识别增大了困难，但其低频线谱仍然存在并且较强，这使得目标信息提取的工作向低频转移。

目标深度信息同样隐藏于低频线谱中，文献[1]指出可通过不同深度的2个接收水听器的声压互谱分析来提取。孙国仓等^[2]研究了Pekeris波导中简正波声强流的分布特性并将其应用于判决声源相对于某一特定深度的位置。余赟等^[3]提出依据2个不同深度接受水听器声压互谱的有功分量的正负来分辨水面水下目标，并指出通过调节阵元两个接收阵元的深度可以是根据有功分量估计出的临界深度，不随距离的变化而起伏变化。并通过公式估计出了阵元的布放深度。但是此方法中若声源布放深度有误差将不可避免的使临界深度随着距离的变化而起伏变化，从而对估计结果产生干扰。本文从理论上分析了临界深度随着距离起伏变化的原因，并据此提出一种用无功分量来补偿有功分量的方法，分析过程中要预先知道声源与接收之间的距离，最后得到的结果为对于任意的接收水听器深度，其互谱的临界深度都不随距离的变化而起伏变化。

本文第1部分介绍声压互谱和基于有功分量的水面水下目标分辨；第2部分提出基于无功分量补偿的水面水下目标分辨；第3部分进行仿真分析；第4部分将第2部分结果应用于垂直阵上进行噪声分析；第5部分是全文总结。

1 互谱分析和目标分辨

先建立一个等声速环境的波导模型，具体如图 1所示。

依据简正波理论，在接收器距离r、接收器深度z_r 、目标深度z_s 处的接收声压 $p(r,{z_r},{z_s},\omega )$ 表达式可简写为^[4]：

$\begin{split}\\[-12pt] p(r,{z_r},{z_s},\omega ) \approx \displaystyle\frac{j}{{\sqrt {8\text{ }\!\!\pi\!\!\text{ } r} \rho \left( {{z_s}} \right)}}{e^{ - j\displaystyle\frac{\text{ }\!\!\pi\!\!\text{ } }{4}}}\sum\limits_{m = 1}^\infty {{\psi _m}} {\times}\\ \left( {{z_s}} \right){\psi _m}\left( {{z_r}} \right)\displaystyle\frac{{{e^{j{k_{rm}}r}}}}{{\sqrt {{k_{rm}}} }}{\text{=}} \displaystyle\sum\limits_{m = 1}^N {{B_m}({z_r},{z_s})} {e^{j({k_{rm}}r - \text{ }\!\!\pi\!\!\text{ } /4)}{\text{，}}} \end{split}$

(1)

式中： ${k_{rm}}$ 为第m号简正波的本征值； ${\psi _m}(z)$ 为m号模的模深度函数；ρ为海水密度。

${B_m}({z_r},{z_s}) = \frac{{{\psi _m}\left( {{z_s}} \right){\psi _m}\left( {{z_r}} \right)}}{{\sqrt {8\text{ }\!\!\pi\!\!\text{ } {k_{rm}}r} \rho ({z_s})}}{\text{，}}$

(2)

可以看出 ${B_m}({z_r},{z_s})$ 为实数。分别定义在目标深度为z_s 、距离为r的2个深度分别为z₁和z₂的接收声压为 ${p_1}(r,{z_1},{z_s},\omega )$ 和 ${p_2}(r,{z_2},{z_s},\omega )$ ，两者间的互谱表示为 $I(r,{z_1},{z_2},{z_s})$ ，则下面关系式成立。

$\begin{split}\\[-12pt] I(r,{z_1},{z_2},{z_s}) \equiv \langle {p_1}{p_2}^*\rangle = \sum\limits_n {{B_n}({z_1},{z_s})} B_n^*({z_2},{z_s}){\text{+}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \sum\limits_m {\sum\limits_{n \ne m} {{B_n}({z_1},{z_s})B_m^*({z_2},{z_s}){e^{j\Delta {k_{mn}}r}}} } {\text{，}} \end{split}$

(3)

其中 $\Delta {k_{mn}}$ 为第m号模和第n号模的水平波数之差，即 $\Delta {k_{mn}} = {k_{rm}} - {k_{rn}}$ 。此互声强I中的实部被称为有功分量，而虚部被称为无功分量。当处理的频率只激发出两阶简正模时，有功分量和无功分量为：

$\begin{split}\\[-12pt] {\rm{real}}\left( {I(r,{z_1},{z_2},{z_s})} \right) \!\!=\!\! {B_1}({z_1},{z_s})B_1^*({z_2},{z_s}) + {B_2}({z_1},{z_s}){\times}\\ B_2^*({z_2},{z_s}) \!\!+\!\! \left( {{B_1}({z_1},{z_s})B_2^*({z_2},{z_s}) + {B_2}({z_1},{z_s})} \right.{\times}\quad\\ \left. {B_1^*({z_2},{z_s})} \right)*\cos \left( {\Delta {k_{12}}r} \right){\text{，}}\quad\quad\quad\quad\quad\quad\quad\quad \end{split}$

(4)

$\begin{split}\\[-12pt] {\rm{imag}}\!\left( {I(r,{z_1},{z_2},{z_s})} \right) \!\!=\!\! {B_1}({z_1},{z_s})B_2^*({z_2},{z_s})\!*\!\sin \left( {\Delta {k_{12}}r} \right){\text{-}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; {B_2}({z_1},{z_s})B_1^*({z_2},{z_s})\!*\!\sin \left( {\Delta {k_{12}}r} \right){\text{，}} \end{split}$

(5)

文献[3]表明，接收声压互谱有功分量的正负号与声源深度有关，可据此来判断水面水下目标。

双水听器声压互谱函数有功分量深度辨识就是将分析得到的有功分量进行正负判决，即阀值化处理。

$ {I^{'}}\left( {r,{z_1},{z_2},{z_s}} \right) = \left\{ {\begin{array}{*{20}{c}} {1{\text{，}}\begin{array}{*{20}{c}} {} {{\rm{real}}\left( {I\left( {r,{z_1},{z_2},{z_s}} \right)} \right) > 0}{\text{，}} \end{array}}\\ {0{\text{，}}\begin{array}{*{20}{c}} {} {{\rm{real}}\left( {I\left( {r,{z_1},{z_2},{z_s}} \right)} \right) < 0}{\text{，}} \end{array}} \end{array}} \right.$

(6)

其中 $I\left( {r,{z_1},{z_2},{z_s}} \right)$ 为式（3）中的互声强。

当2个听器深度为z₁和z₂固定时，预使互声强有功分量的正负号不随水平距离变化，则有

${B_1}({z_1},{z_s})B_2^*({z_2},{z_s}) + {B_2}({z_1},{z_s})B_1^*({z_2},{z_s}) = 0{\text{，}}$

(7)

此时有功分量变为：

$\begin{split}\\[-12pt] {\rm{real}}\left( {I(r,{z_1},{z_2},{z_s})} \right) = {B_1}({z_1},{z_s})B_1^*({z_2},{z_s})+\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; {B_2}({z_1},{z_s})B_2^*({z_2},{z_s}){\text{，}} \end{split}$

(8)

从式（2）可看出， ${B_m}({z_n},{z_s})$ 的幅值随着距离r的增大而单调减小，但其正负号保持不变。所以式（8）对应的 ${z_n}$ 和z_s深度处接收声压互谱产生的临界深度不随距离的变化而起伏变化。但如果上述等式不成立则由于差模分量的影响使得在正负号的临界处起伏变化，影响结果判断。下面本文提出一种方法对任意的接收深度，其声压互谱都不随距离r的变化而起伏变化。

2 用无功分量补偿分辨目标

先将式（3）对应的声压互谱重新划分为同模分量和差模分量：

$C\left( {r,z} \right) = \sum\limits_n {{B_n}({z_1},{z_s})} B_n^*({z_2},{z_s}){\text{，}}$

(9)

$\varGamma\left( {r,z} \right) = 2\sum\limits_m {\sum\limits_{n \ne m} {{B_n}({z_1},{z_s})B_m^*({z_2},{z_s}){e^{j\Delta {k_{mn}}r}}}{\text{，}}} $

(10)

先分析同模分量，假设声场中只存在2阶简正模，则式（9）中同模分量变为：

$\begin{split}\\[-12pt] C(r,{z_1},{z_2},{z_s}) = {B_1}({z_1},{z_s}){B^*}_1({z_2},{z_s}) + {B_2}({z_1},{z_s})\\ B_2^*({z_2},{z_s}) = \frac{1}{{8r{k_{r1}}{k_{r2}}}}({k_{r2}}\psi _1^2({z_s}){\psi _1}\left( {{z_1}} \right){\psi _1}\left( {{z_2}} \right) + \\ {k_{r1}}\psi _2^2\left( {{z_s}} \right) \times \left. {{\psi _2}\left( {{z_1}} \right){\psi _2}\left( {{z_2}} \right)} \right){\text{。}}\quad\quad \end{split}$

(11)

由于 ${B_m}({z_r},{z_s})$ 为实数，可知同模分量为实数，故其全部都为有功分量。

从式（11）第2行可看出，当 ${z_1},{z_2},{z_s}$ 和海洋环境确定以后， $C\left( {r,{z_1},{z_2},{z_s}} \right)$ 便只随r单调变化，并且正负号保持不变。 $C\left( {r,{z_1},{z_2},{z_s}} \right)$ 的正负临界点为：

${k_{r2}}\psi _1^2\left( {{z_s}} \right){\psi _1}\left( {{z_1}} \right){\psi _1}\left( {{z_2}} \right) \!\!+\!\! {k_{r1}}\psi _2^2\left( {{z_s}} \right){\psi _2}\left( {{z_1}} \right){\psi _2}\left( {{z_2}} \right) \!\!=\!\! 0{\text{，}}$

(12)

而当海洋环境确定以后， ${z_1},{z_2},{z_s}$ 就决定了 $C\left( {r,{z_1},{z_2},{z_s}} \right)$ 的正负。因为只考虑了2阶模，简正模的特点为第n号模有n个零点，并且由于海面为压力释放边界，所以各阶模在0 m深处，其模深度函数都为0。

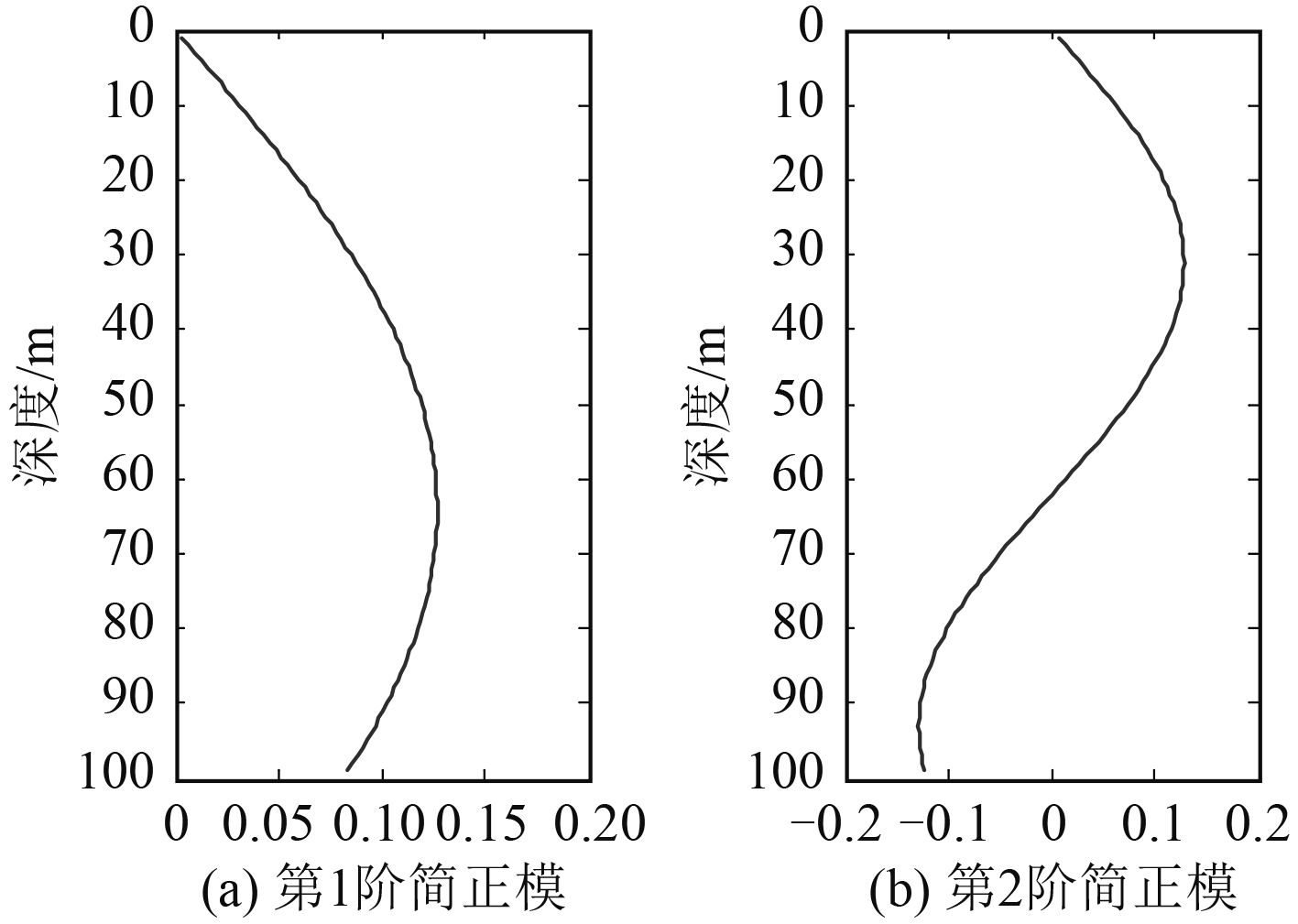
图 2为图 1环境下激发的模深度函数，40 Hz的发射频率只激发了两阶模，第1阶模有1个零点，第2阶模有2个零点。由于第1阶模只有1个零点并且在0 m处为0，所以式（12）中对于任意 ${z_1},{z_2}$ ， ${\psi _1}\left( {{z_1}} \right),{\psi _1}\left( {{z_2}} \right)$ 同号，即 $\psi _1^2\left( {{z_s}} \right){\psi _1}\left( {{z_1}} \right){\psi _1}\left( {{z_2}} \right) > 0$ 。第2阶模有2个零点，第1个零点在0 m处，第2个零点在某一深度处，设此深度为z_h ，所以 $z < {z_h},{\psi _2}\left( z \right) > 0;z > {z_h},{\psi _2}\left( z \right) < 0.$ 式（12）左边第1部分恒为正，预使式（12）成立，则 ${z_n}$ 和 ${z_s}$ 必然在z_h 之间，否则式（12）左半部分恒大于0。式（12）左半部分可化为：

$\frac{{{k_{r2}}\psi _1^2\left( {{z_s}} \right)}}{{{k_{r1}}\psi _2^2\left( {{z_s}} \right)}}{\psi _1}\left( {{z_1}} \right){\psi _1}\left( {{z_2}} \right) + {\psi _2}\left( {{z_1}} \right){\psi _2}\left( {{z_2}} \right){\text{。}}$

(13)

当 ${z_n}$ 和 ${z_s}$ 固定以后且满足 ${z_1} < {z_h} < {z_2}$ 时，调节 ${z_s}$ 即调节 $\displaystyle\frac{{\psi _1^2\left( {{z_s}} \right)}}{{\psi _2^2\left( {{z_s}} \right)}}$ ，就可以改变式（13）的正负。图 3为调节z_s 得到 $\displaystyle\frac{{\psi _1^2\left( {{z_s}} \right)}}{{\psi _2^2\left( {{z_s}} \right)}}$ 的仿真结果，仿真环境与图 2相同，z_s 变化区间为[1, 99]，

图 3中横坐标表示声源深度调节z_s ，纵坐标为归一化以后用dB表示的幅度。图中实线为 $\displaystyle\frac{{\psi _1^2\left( {{z_s}} \right)}}{{\psi _2^2\left( {{z_s}} \right)}}$ 在不同深度的结果，图中虚线表示 ${z_1} = 41 {\rm{m}},{z_2} = 85 {\rm{m}}$ 时 $\displaystyle\frac{{ - {k_{r1}}{\psi _2}\left( {{z_1}} \right){\psi _2}\left( {{z_2}} \right)}}{{{k_{r2}}{\psi _1}\left( {{z_1}} \right){\psi _1}\left( {{z_2}} \right)}}$ 的值。从图中可看出，声源深度在42~84 m时， $\displaystyle\frac{{\psi _1^2\left( {{z_s}} \right)}}{{\psi _2^2\left( {{z_s}} \right)}}$ > $\displaystyle\frac{{ - {k_{r1}}{\psi _2}\left( {{z_1}} \right){\psi _2}\left( {{z_2}} \right)}}{{{k_{r2}}{\psi _1}\left( {{z_1}} \right){\psi _1}\left( {{z_2}} \right)}}$ ，此时式（13）为正；相应的，在此区间之外的式（13）值为负。所以声源深度z_s 影响着接收互声压的正负，其信息包含在正负结果之中。同样调节z₁和z₂接收深度就可以调节临界深度。

从上面的分析过程可看出，同模分量的正负号包含了声源深度信息，所以第1节介绍的方法中临界深度产生主要是由声压互谱的同模分量决定的。并且对于任意布放深度水听器产生的同模分量，其临界深度不随着距离的变化而起伏变化。

差模分量变为：

$\begin{split}\\[-12pt] \Gamma \left( {r,z} \right) = ({B_1}({z_1},{z_s}){B^*}_2({z_2},{z_s}){e^{j*\Delta {k_{12}}r}} +{B_2}({z_1},{z_s})\times \\[3pt] {B^*}_1({z_2},{z_s}){e^{j*\Delta {k_{21}}r}}) = ({B_1}({z_1},{z_s})B_2^*({z_2},{z_s}) + \\[3pt] {B_2}({z_1},{z_s})B_1^*({z_2},{z_s}))*\cos \left( {\Delta {k_{12}}r} \right) + i*({B_1}({z_1},{z_s})\\[3pt] B_2^*({z_2},{z_s}) - {B_2}({z_1},{z_s})B_1^*({z_2},{z_s}))*\sin \left( {\Delta {k_{12}}r} \right) {\text{。}} \end{split}$

(14)

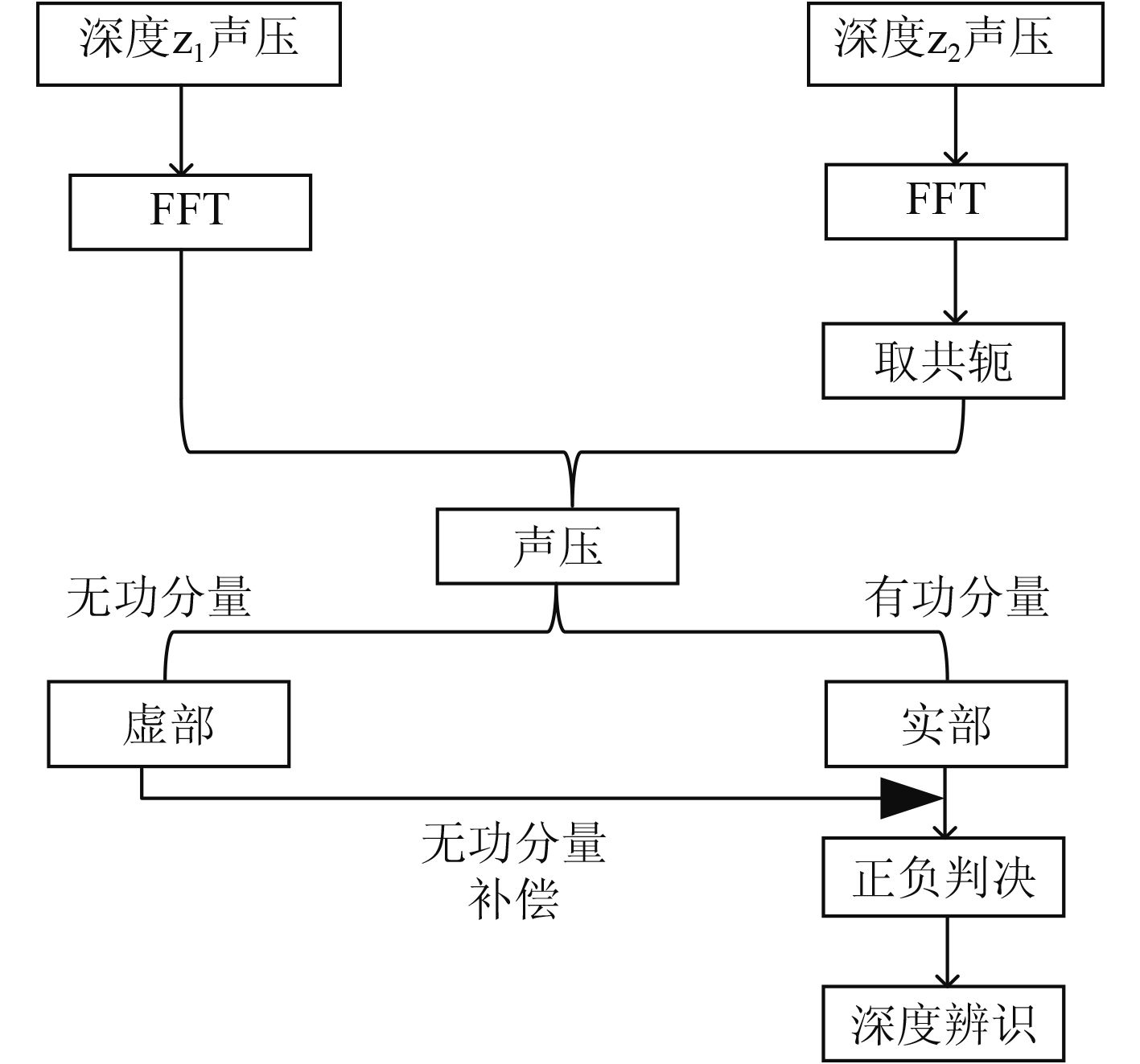
从式（14）可看出，差模分量的实部属于有功分量，虚部为无功分量，并且差模分量与距离有关，其随距离变化而起伏变化，其中有功分量成分也随着距离r的变化而起伏变化。所以差模分量对应的有功分量使得第1节介绍的方法会随着距离的变化而起伏变化，对估计结果产生影响。上面从理论上分析了临界深度随着距离的变化而起伏变化的原因，下面提出一种用无功分量来补偿有功分量中的差模分量的方法，从而分离得到同模分量使得对于任意布放深度的两个阵元其声压互谱不随距离的变化而起伏变化。原理框图如图 4所示

在只激发两阶简正模的情况下，根据式（2）、式（4）和式（5），无功分量和有功分量可化简为

$\begin{split}\\[-12pt] {\rm{real}}\left( {I(r,{z_1},{z_2},{z_s})} \right) = {B_1}({z_1},{z_s})B_1^*({z_2},{z_s}) + {B_2}({z_1},{z_s}) \times \\[3pt] B_2^*({z_2},{z_s}) + \frac{{{\psi _1}\left( {{z_s}} \right){\psi _2}\left( {{z_s}} \right)}}{{8\text{ }\!\!\pi\!\!\text{ } r\sqrt {{k_{r1}}{k_{r2}}} }}({\psi _1}\left( {{z_1}} \right){\psi _2}\left( {{z_2}} \right) + \\[3pt] {\psi _2}\left( {{z_1}} \right){\psi _1}\left( {{z_2}} \right)) \times \cos \left( {\Delta {k_{12}}r} \right) {\text{，}} \end{split}$

(15)

$ \begin{split}\\[-12pt] {\rm{imag}}\left( {I(r,{z_1},{z_2},{z_s})} \right)\; = \displaystyle\frac{{{\psi _1}\left( {{z_s}} \right){\psi _2}\left( {{z_s}} \right)}}{{8\text{ }\!\!\pi\!\!\text{ } r\sqrt {{k_{r1}}{k_{r2}}} }}{\times}\qquad\qquad\\[3pt] \quad \quad\left( {{\psi _1}\left( {{z_1}} \right){\psi _2}\left( {{z_2}} \right) - {\psi _2}\left( {{z_1}} \right){\psi _1}\left( {{z_2}} \right)} \right)\sin \left( {\Delta {k_{12}}r} \right){\text{。}} \end{split} $

(16)

式中： $I\left( {r,{z_1},{z_2},{z_s}} \right)$ 为不同接收深度的互声强； ${B_m}\left( {{z_n},{z_s}} \right)$ 由式（2）定义。

式（15）中有功分量等号右边前两部分为同模分量，第3部分为差模分量；无功分量都为差模分量。从中可看出，无功分量和有功分量中的差模分量是相关的，而无功分量可以通过接收信号估计出来的，如果声源距离r已知，波导环境已知，则可以通过虚部来抵消掉有功分量中差模分量的耦合量，从而推出同模分量，可以用来分辨水面水下目标。

波导环境已知，则模深度函数可通过kraken^[5]求得，在结合声源距离r，则可分析得到两者间的关系。

设

$\begin{split}\\[-12pt] A(r) = \displaystyle\frac{{\left( {{B_1}({z_1},{z_s})B_2^*({z_2},{z_s}) + {B_2}({z_1},{z_s})B_1^*({z_2},{z_s})} \right)}}{{\left( {{B_1}({z_1},{z_s})B_2^*({z_2},{z_s}) - {B_2}({z_1},{z_s})B_1^*({z_2},{z_s})} \right)}}=\\[3pt] \;\;\;\;\;\;\; \displaystyle\frac{{\left( {{\psi _1}\left( {{z_1}} \right){\psi _2}\left( {{z_2}} \right) + {\psi _2}\left( {{z_1}} \right){\psi _1}\left( {{z_2}} \right)} \right)\cos \left( {\Delta {k_{12}}r} \right)}}{{\left( {{\psi _1}\left( {{z_1}} \right){\psi _2}\left( {{z_2}} \right) - {\psi _2}\left( {{z_1}} \right){\psi _1}\left( {{z_2}} \right)} \right)\sin \left( {\Delta {k_{12}}r} \right)}}{\text{，}} \end{split}$

(17)

则同模分量为：

$\begin{split}\\[-12pt] \varGamma \left( {r,z} \right) = real(I(r,{z_1},{z_2},{z_s})) - \qquad \qquad \qquad \qquad\\ A\left( r \right)*{\rm {imag}}(I(r,{z_1},{z_2},{z_s})) \times \cot (\Delta {k_{12}}r){\text{。}} \end{split}$

(18)

式（14）中的参量都已知，或可以通过水听器测得，由此可得到任意深度接收信号的同模分量，在用其分辨水面水下目标。

3 仿真分析

波导环境如图 1所示，波导深度H=100 m，仿真频率为40 Hz (见图 2)，此频率只激发了2阶模。研究表明，同模分量对声速剖面有一定的宽容性，所以本文分析的等声速环境对其他声速环境仍然适用。

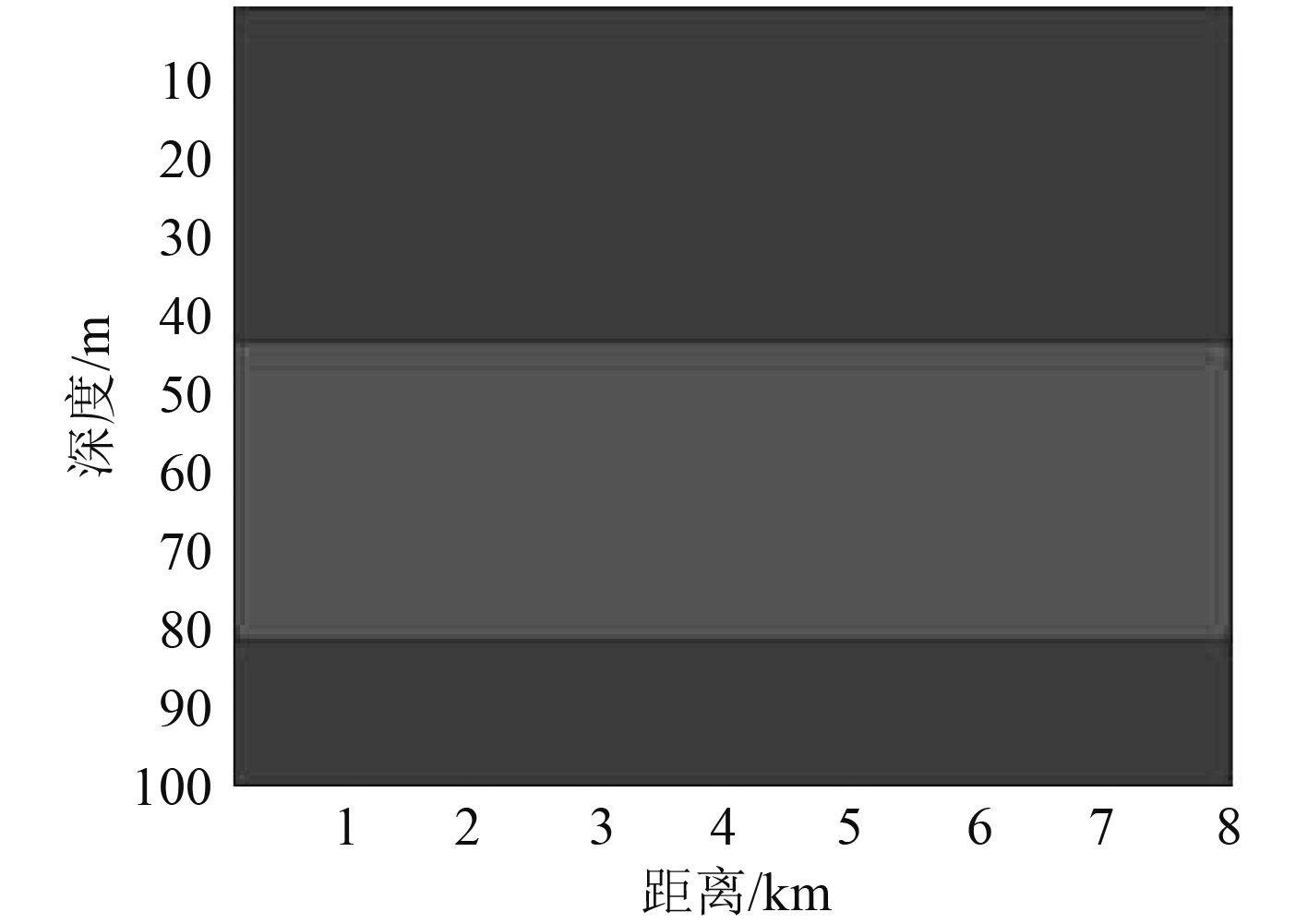
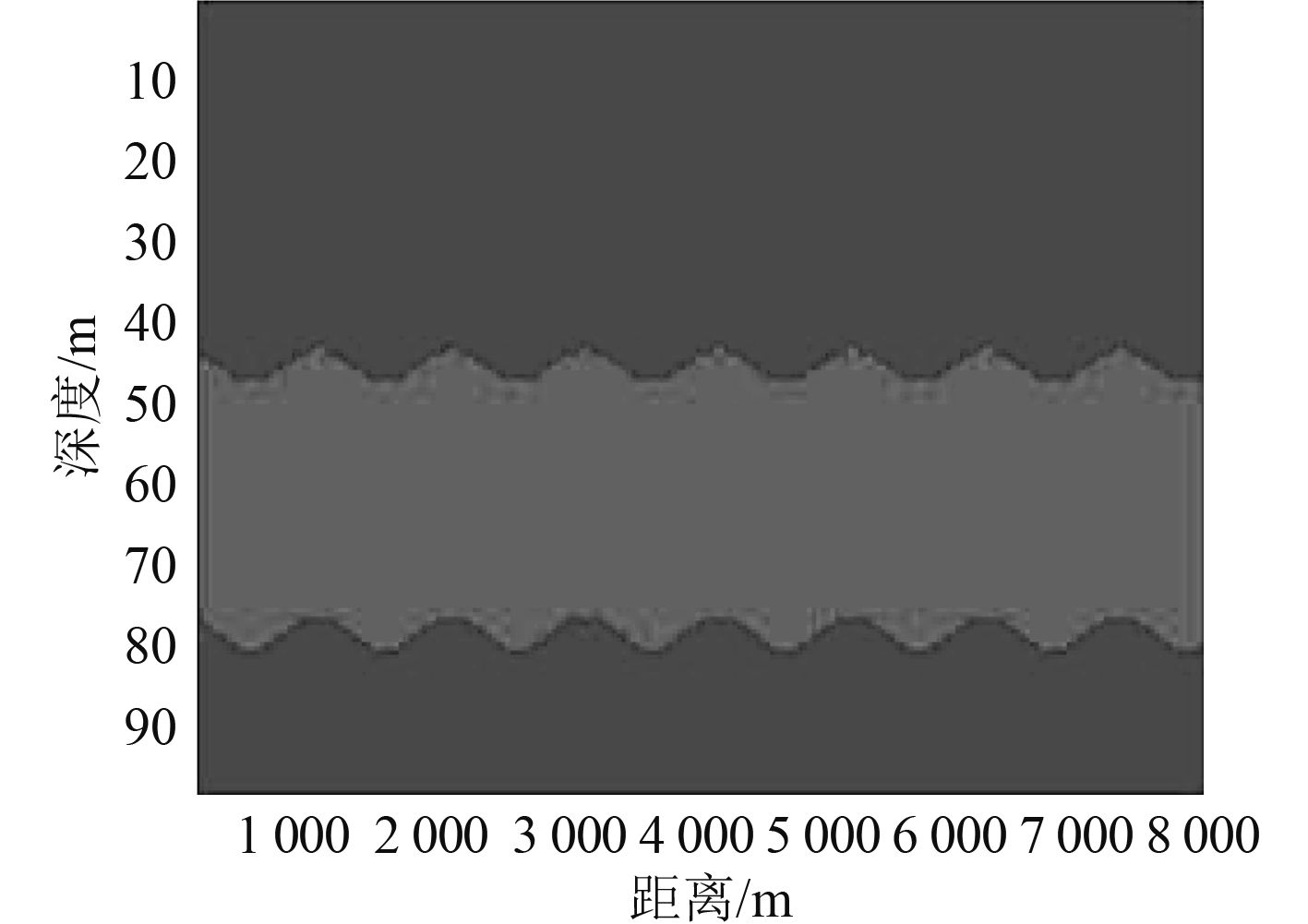
当接收深度z₁=41 m，z₂=85 m时，式（10）成立，经过式（9）阀值化处理以后的结果如图 5所示，图 6是接收深度z₁=35 m，z₂=85 m时的结果。

由于图 5环境下式（10）成立，差模分量为0，所以有功分量中只有同模分量，可以看出阀值化以后的结果不随距离r的变化而起伏变化，当声源距离在临界值（42 m）以上（结果为负）时判断为水面目标（对于85~100 m的结果同样为负，但假定目标不可能在如此贴近海底的深度行驶），当其在临界值以下（45~84 m）（结果为正）时判断为水下目标。从而可以看出此方法能分辨出水面水下目标。而图 6是差模分量不为0时的结果，从中可看到临界值随着距离r起伏变化，这对水面水下目标的分辨产生了一定影响。

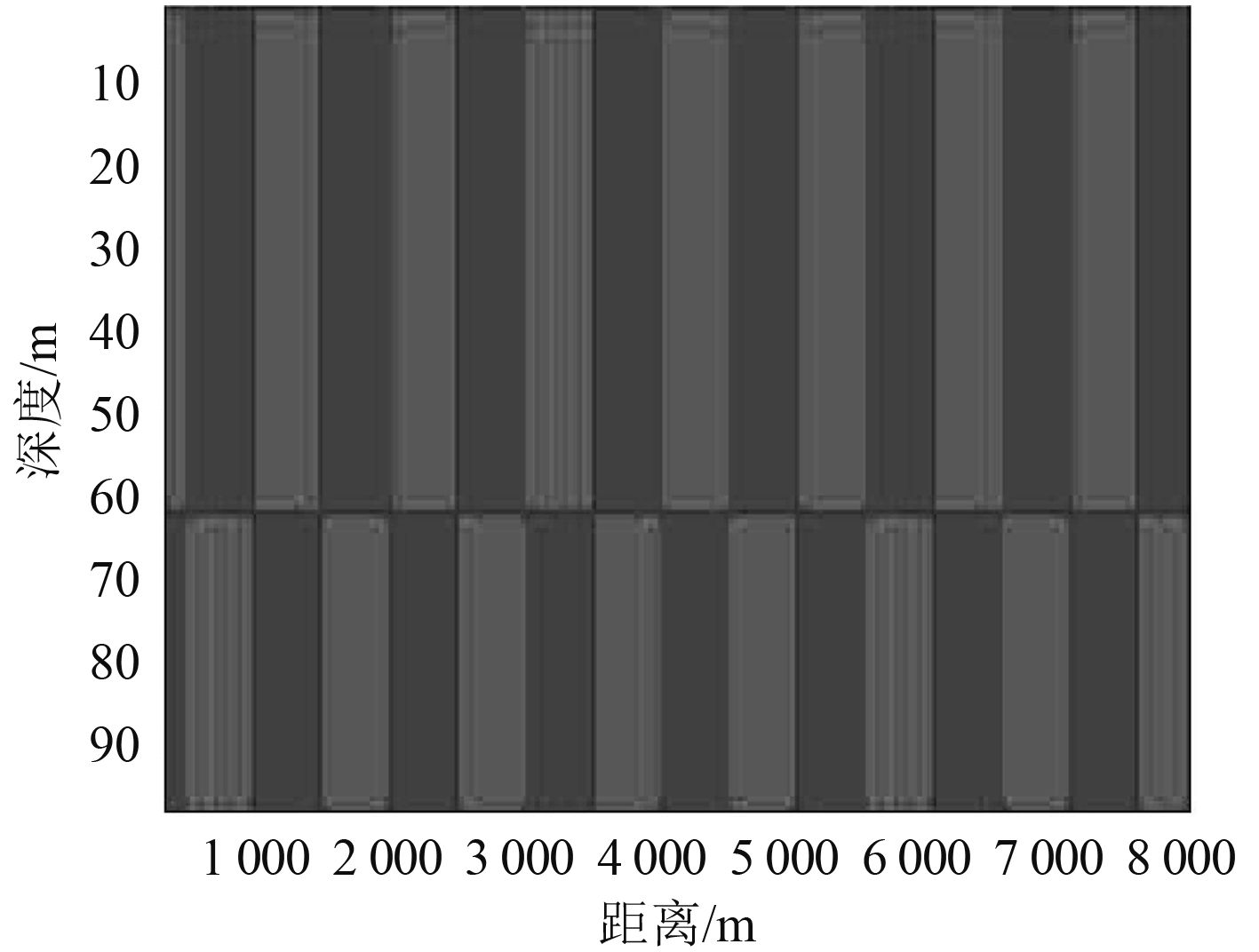
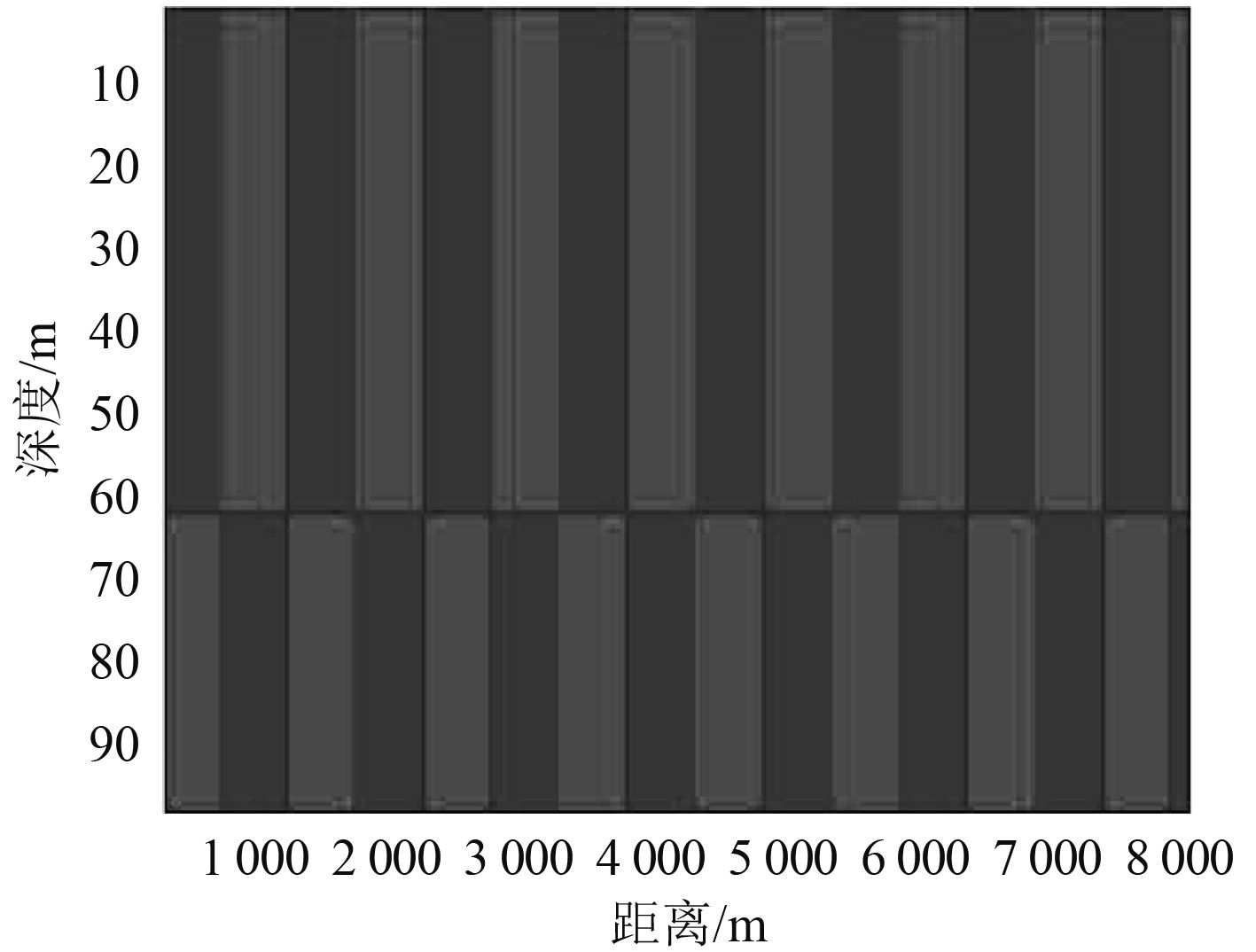
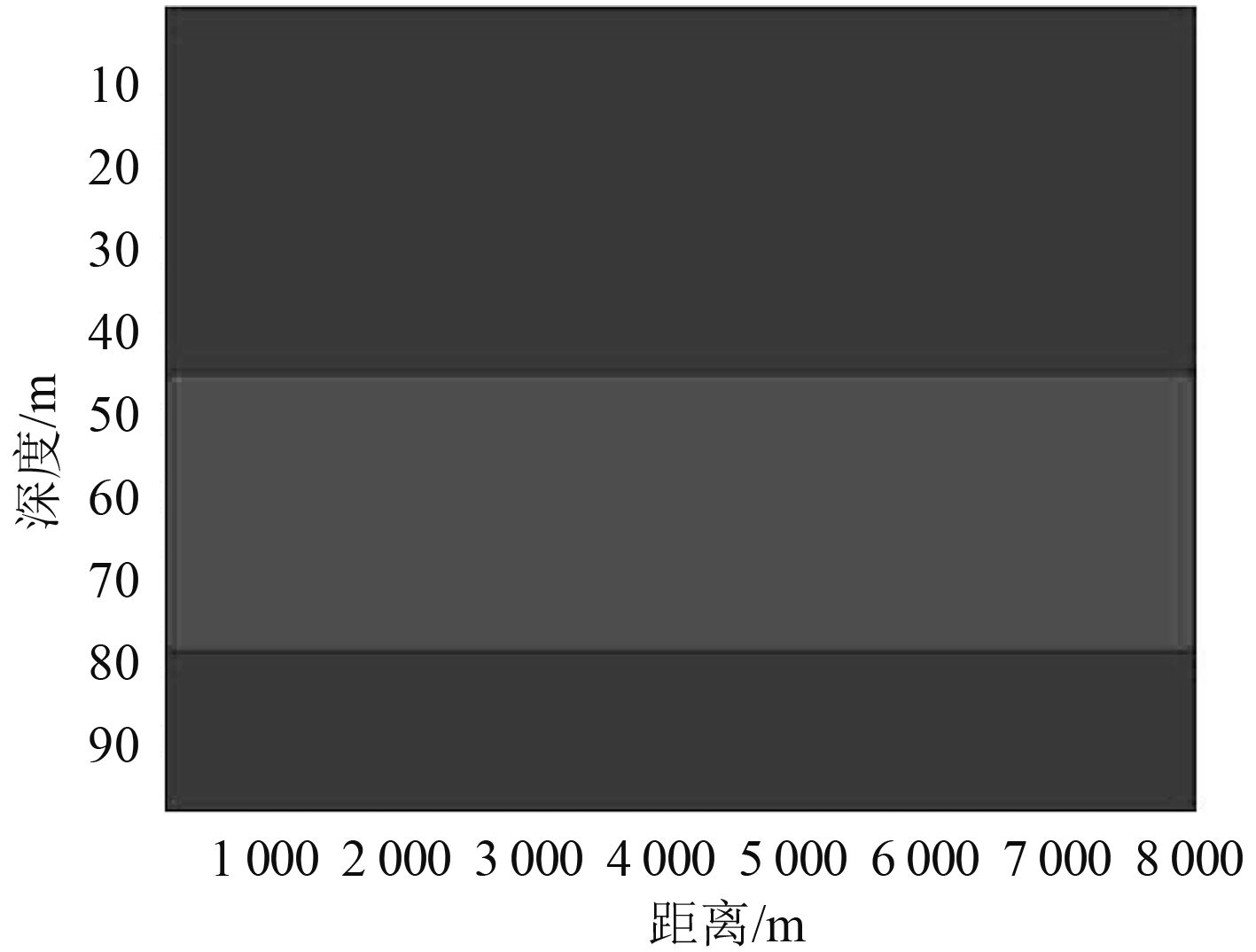
图 7~图 9仍是图 1在环境下接收深度为z₁=35 m，z₂=85 m的仿真结果，其中图 7是有功分量中的差模分量，图 8是无功分量，即互声强的虚部，图 9是用式（14）推导得到的同模分量的结果。与图 6相比可以看到，通过无功分量补偿后，阀值化以后的结果不再随距离变化而起伏变化，将同模分量与差模分量的耦合解开。图 9与图 5相比临界深度有所不同，这是由于两阵元接收深度不同造成的。

4 噪声干扰下的深度分辨

第2部分和第3部分分析了用双水听器分析水面水下目标的方法，但是分析过程中没有考虑噪声的影响，实际上前面分析都是以0为阀值来分辨目标，噪声对这种方法的性能影响很大。

图 10是加了3 dB信噪比的噪声以后分离的同模分量的估计结果。仿真环境如图 1所示，两阵元接收深度分别位于35 m和85 m。从中可以看出噪声对估计结果影响很大，此时此方法已经不能正常使用。

用垂直阵和一个不同深度全向水听器联合分辨水面水下目标进行分析。由于全向水听器和垂直阵的每个阵元接收线谱的互声强的同模部分都可以进行声源水面水下目标分辨，可将垂直阵上每个阵元得到的互谱同模分量空间叠加，增强信号能量，提高信噪比。即通过不同深度的数据累计来提高信噪比。

仿真分析用垂直阵和一个不同布放深度的全向水听器来分辨水面水下目标。仿真过程中，用32阵元垂直阵，仿真环境如图 1所示，单水听器的布放深度在85 m，32阵元垂直阵布放深度从20 m到51 m，以1 m为间隔。仿真结果如图 11所示。

图 11经过空间积累以后的结果与图 10相比，分辨结果更加准确，抗干扰能力更强。适用于实际应用。

5 结语

本文介绍了现有的利用有功分量来分辨水面水下目标的方法；基于信号特性提出利用无功分量补偿的改进方法，并进行仿真分析。本文提出的方法需要有声源与接收之间距离的先验信息，结合海洋环境，可分离有功分量中的同模分量，使得用于分辨水面水下目标的临界深度对任意布放深度的水听器都没有要求。将本文提出的方法应用到垂直阵上，达到了抗噪声，提高信噪比的效果。在噪声干扰下能有效地分辨出水面水下目标，