0 引言

水下可见光通信是一种以光波为信息载体，以水为媒介，以点对点方式进行信息传输，最终完成信息交互的通信技术。相对于甚低频、水声等通信方式，水下可见光通信的信息容量大、传播速率快^[1]，抗电磁干扰能力强、安全性高，收发设备体积小、成本低，在水下传感器数据回收、对潜通信等领域有广泛的应用前景。

光在海水中传输比在大气中的传输更易衰减，这是由于海水中有机物和无机物的浓度更高，影响着光的吸收与散射。建模仿真方法能够实现大样本的模拟实验，是研究水下光通信空间特性的有效途径，其中，采用蒙特卡洛法模拟光分子运动轨迹^[2]或解决辐射传输方程较为常见^[3]，但蒙特卡罗仿真的计算量大、周期长，且针对每一种场景均需要设置复杂的模型参数，工程实现的要求高；传统的比尔定律计算较为简单，但该方法将终端光斑视为平均分布，准确性欠佳。本文通过研究海水信道的光学特性，构建了高斯光源的光束传播函数，形成了操作简捷、结果准确的水下光通信信道空间特性研究方法。

1 海水信道的光学特性

理解海水的光学特性是建立水下光学信道模型的基础。海水对光的作用主要分为吸收与散射，光被吸收和散射的程度主要受海水中物质浓度影响，同时也与光源的波长有关，而水中物质浓度是由水质类型决定。在本文研究中将条件设置为一类水质以及部分二类水质中，叶绿素浓度为0~12 mg/m³，即开放海域以及生物纯近岸海域^[4]。本节通过将海水中各要素浓度进行转化，建立光的衰减模型。

1.1 吸收

1）造成光在水下传输时被吸收的主要因素包括水分子、浮游植物、有机碎屑与矿物颗粒以及溶解有机物（CDOM），建立光的吸收模型为：

$a(\lambda )={{a}_{w}}(\lambda )+{{a}_{p}}(\lambda )+{{a}_{d}}^{{}}(\lambda )+{{a}_{c}}^{{}}(\lambda ){\text {。}}$

(1)

式中； $\lambda $ 为光的波长； $a(\lambda )$ 为吸收因子； ${{a}_{w}}(\lambda )$ 为水分子的吸收因子； ${{a}_{p}}(\lambda )$ 为浮游植物的吸收因子； ${{a}_{d}}(\lambda )$ 为有机碎屑与矿物颗粒的吸收因子； ${{a}_{c}}(\lambda )$ 为溶解有机物的吸收因子。

2）综合文献[4-5]，将各吸收因素浓度转化为叶绿素浓度进行计算，建立生物光学吸收模型为：

$\begin{split}\\[-12pt] a(\lambda ) = {a_w}(\lambda ) + {a_p}^0(\lambda ){\left( {{C_c}/{C_c}^0} \right)^{0.602}} +\quad \\ {a_d}^0{C_h}\exp ( - {k_d}\lambda ) + {a_f}^0{C_f} \times \quad \quad \\ \quad \quad \quad \quad exp ( - {k_f}\lambda ) + {a_h}^0{C_h}\exp ( - {k_h}\lambda ){\text{。}}\\ \end{split}$

(2)

式中： ${{a}_{p}}^{0}(\lambda )$ 为叶绿素光谱吸收系数，是叶绿素在进行光合作用时产生的； ${{a}_{w}}(\lambda )$ 和 ${{a}_{p}}^{0}(\lambda )$ 可采用直接测量的方法获得，如表 1所示； ${{C}_{c}}$ 为叶绿素浓度，mg/m³； ${{C}_{c}}^{0}$ 为浓度常数，通常按1 mg/m³计算； ${{a}_{d}}^{0}$ 为有机碎屑与矿物颗粒吸收系数； ${{a}_{f}}^{0}$ 和 ${{a}_{h}}^{0}$ 分别为黄腐酸、腐植酸光谱吸收系数。 ${{k}_{d}}$ ， ${{k}_{f}}$ ， ${{k}_{h}}$ 分别为有机碎屑与矿物颗粒、黄腐酸、腐植酸吸收曲线斜率，具体数值参见表 2。

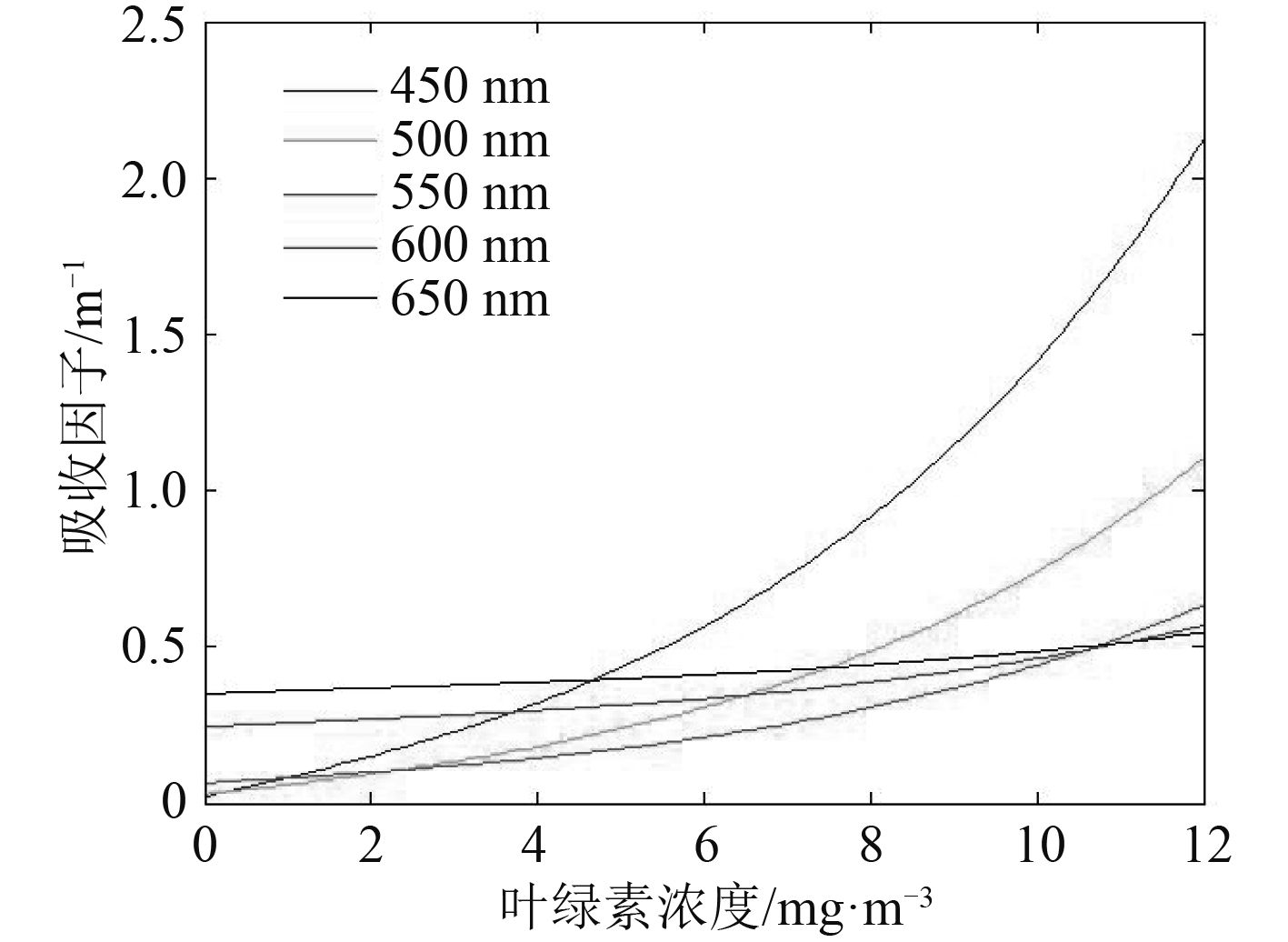
3）基于上述模型，绘制出5种典型波长光的吸收因子与叶绿素浓度之间的关系，如图 1所示。

通过分析图 1可知，吸收因子会随叶绿素浓度的增加而递增，而不同波长光的吸收因子随叶绿素浓度变化的幅度也存在较大差异，因此在水下光通信应用中，应根据水质情况选择相应波段的光源，降低其在水中的吸收衰减。

1.2 散射

1）散射是指光在传输时，与海水中微粒发生碰撞，而改变其直线轨迹的现象。造成光在水下传输时散射的主要因素包括：水分子、浮游植物、悬浮颗粒及溶解有机物。其中，悬浮颗粒和溶解有机物造成光的散射程度，主要是由颗粒体积决定，因此可将其分为大颗粒与小颗粒研究。首先建立光的散射模型为：

$b(\lambda )={{b}_{w}}(\lambda )+{{b}_{p}}^{{}}(\lambda )+{{b}_{s}}^{{}}(\lambda )+{{b}_{l}}^{{}}(\lambda ){\text {。}}$

(3)

式中： $\lambda $ 为光的波长； $b(\lambda )$ 为散射因子； ${{b}_{w}}(\lambda )$ 为水分子的散射因子； ${{b}_{p}}(\lambda )$ 为浮游植物的散射因子； ${{b}_{l}}(\lambda )$ 为大颗粒的散射因子； ${{b}_{s}}(\lambda )$ 为小颗粒的散射因子。

2）综合文献[3-5]，将各散射因素浓度转化为叶绿素浓度进行计算，建立生物光学散射模型为：

$\begin{split}\\[-12pt] b(\lambda ) = 0.005826{(400/\lambda )^{4.32}} + {(550/\lambda )^{}}0.3{C_c}^{0.62} + \\ \quad \quad {\rm{1}}{\rm{.151302}}{\left( {400/\lambda } \right)^{1.17}}{\rm{0}}{\rm{.01739}}{C_c}\times\\ \quad \quad \exp \left( {0.11631\left( {{C_c}/{C_c}^0} \right)} \right) \!\!+\!\! {\rm{0}}{\rm{.341074}}{\left( {400/\lambda } \right)^{0.3}}\times\\ \quad \quad {\rm{0}}{\rm{.76284}}{C_c}\exp \left( {0.03092\left( {{C_c}/{C_c}^0} \right)} \right){\text{。}} \end{split}$

(4)

3）基于上述模型，绘制出4种物质的散射因子与叶绿素浓度之间的关系，如图 2所示。

通过分析图 2可知，在水下光传输中，大颗粒造成的散射影响最大，水分子造成的散射影响最小。而大颗粒造成的是米氏散射，主要为小角度前向散射。

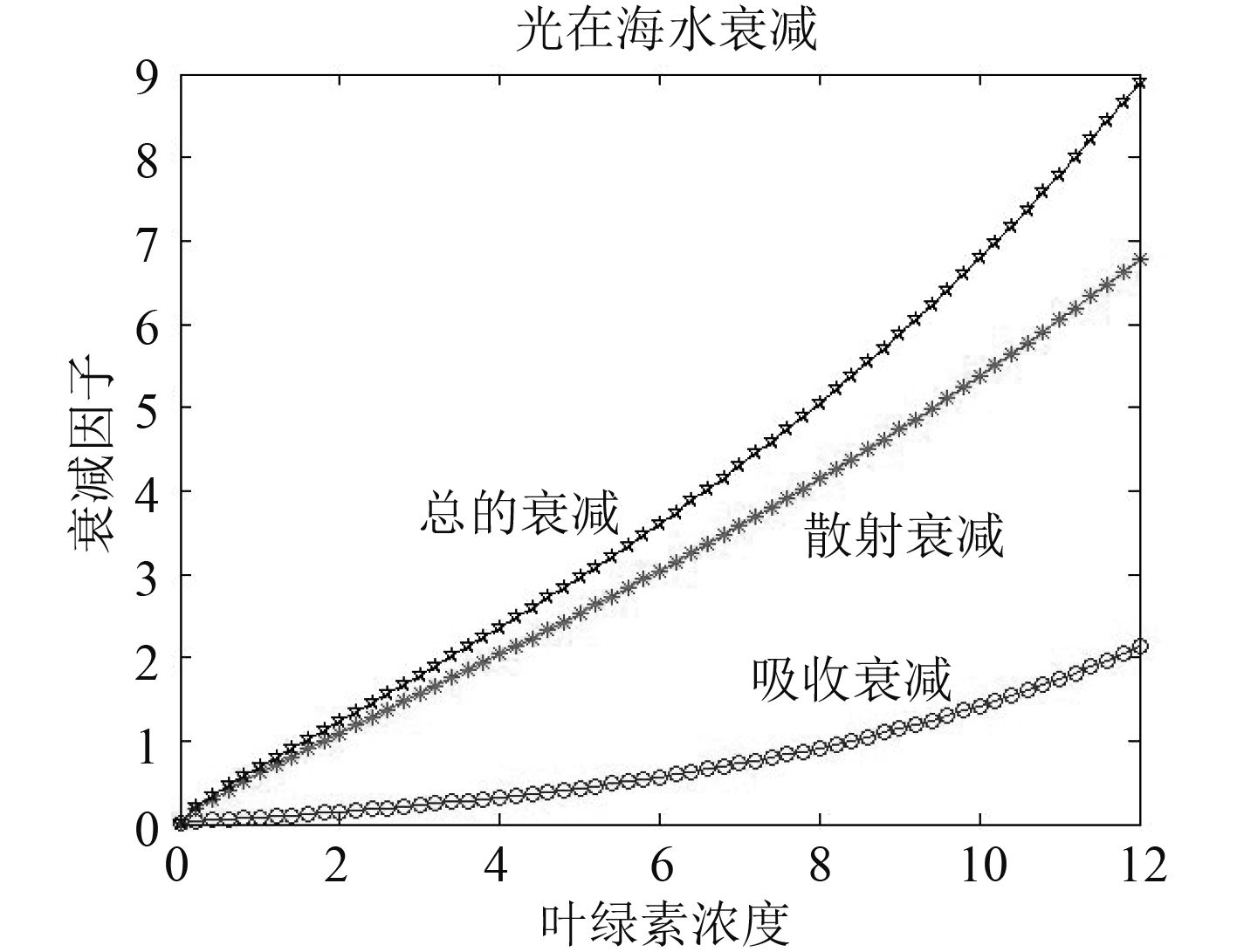
综上所述，光在水中的衰减主要包括吸收和散射，衰减程度如图 3所示。随着叶绿素浓度的增加，光的吸收和散射因子均呈递增趋势，而散射衰减的增速更快、影响更大。

2 接收端光功率分布研究

要开展水下光通信的工程应用，必须实现光的有效接收，而研究接收端的光功率分布是其重要基础。本节通过建立光束传播函数（BSF）模型，能够较为准确地计算光被吸收和散射的能量损耗，预测接收端的光功率分布情况，从而估计光通信的有效范围。

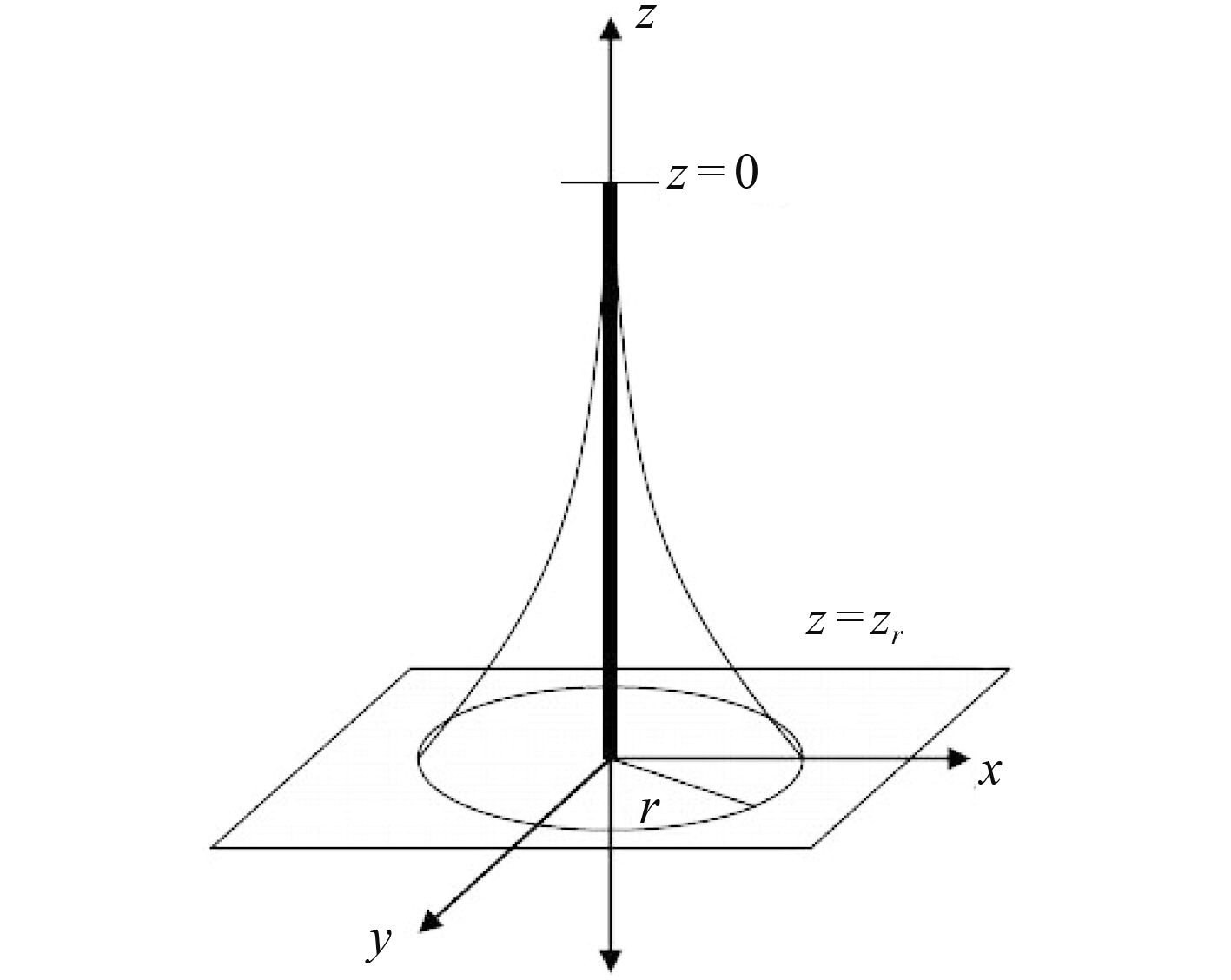
研究BSF的空间模型如图 4所示。光源位于z=0的位置，BSF研究的是当接收光斑落于z=z_r平面内，与光轴线距离为r时的光能量分布。其研究的条件为：一是海水中光的散射主要为小角度前向散射；二是光功率相对于光束轴是对称分布；三是不考虑光在距离大于z_r时发生的散射；四是传输媒介为均匀介质。同时本文只研究单光源散射，而不考虑光源阵列的叠加分布。

BSF计算公式为：

$BSF(r,{z_r}) = \frac{1}{{2\text{ }\!\!\pi\!\!\text{ } }}\int_0^\infty {E(v,{z_r})} S(v,{z_r}){J_0}\left( {vr} \right)v{\rm{d}}v{\text {。}}$

(5)

式中： $E(v,{{z}_{r}})$ 为光源分布函数； $S(v,{{z}_{r}})$ 为媒介光传输函数； $J_{_{0}}^{{}}\left( vr \right)$ 为贝塞尔函数。

2.1 光源分布函数

水下光通信一般采用的LED和激光作为光源，通常可用高斯分布表达，高斯光源在自由空间的分布为^[7]：

$e(r,{{z}_{r}})=\frac{{{P}_{0}}}{2\pi {{V}_{0}}({{z}_{r}})}\exp [\frac{-{{r}^{2}}}{2{{V}_{0}}({{z}_{r}})}]{\text{，}}$

(6)

式中： ${{P}_{0}}$ 为初始能量； ${{z}_{r}}$ 为光束沿光轴传输距离；r为接收端偏离光轴的距离； ${{V}_{0}}({{z}_{r}})$ 为高斯光源在自由空间的方差。可由光束发散角 $w$ 计算得到：

$\sqrt{{{V}_{0}}({{z}_{r}})}={{z}_{r}}\tan (\frac{w}{2})\pi {\text{，}}$

(7)

空间域 $\left( r,{{z}_{r}} \right)$ 到同等系统频域 $\left( v,{{z}_{r}} \right)$ 的变换通常使用傅里叶变换，由于光源是轴对称的，因此对式（6）采用汉克尔变换简化，结果如下：

$E(v,{{z}_{r}})={{P}_{0}}\exp [\frac{-{{V}_{0}}({{z}_{r}}){{v}^{2}}}{2}]{\text{。}}$

(8)

2.2 媒介光传输函数（optical transfer function，OTF）

OTF是媒介对光脉冲响应的傅里叶变换，它描述光信号经过水体传输后的空间特性。由于光在海水中主要为小角度散射，可采用小角度近似： $\sin \theta \approx \theta $ ， $\cos \theta \approx 1$ ；通过对散射媒介的微积分运算，能够建立OTF与吸收和散射之间的关系^[8]：

$S(v,{z_r}) = \exp \left\{ { - \int_0^{{z_r}} {[c\lambda - b} \lambda P(v({z_r} - z))]dz} \right\}{\text{，}}$

(9)

式中： $c\lambda $ 为总的衰减因子； $b(\lambda )$ 为散射因子； $P(v)$ 为体散射函数，是由散射相位函数 $p(\theta )$ 经过汉克尔变换得到，如下式：

$P(v) = 2\text{ }\!\!\pi\!\!\text{ } \int_0^\text{ }\!\!\pi\!\!\text{ } {p\left( \theta \right)} {J_0}\left( {\theta v} \right)\theta {\rm{d}}\theta {\text{，}} $

(10)

式中：θ为散射角； $J_{_{0}}^{{}}\left( z \right)$ 为贝塞尔函数。表达式为：

$J_{_{0}}^{{}}\left( z \right)=\sum\limits_{k=0}^{\infty }{\frac{{{(-1)}^{k}}{{z}^{2k}}}{{{\left( k! \right)}^{2}}{{2}^{2k}}}}{\text{，}}$

(11)

将贝塞尔函数展开式代入式（10），获得体散射函数表达式为：

$P(v) = 2\text{ }\!\!\pi\!\!\text{ } \int_0^\text{ }\!\!\pi\!\!\text{ } {p\left( \theta \right)} (1 - \frac{{{{(\theta v)}^2}}}{4} \!\!+\!\! \frac{{{{(\theta v)}^4}}}{{64}} - \frac{{{{(\theta v)}^6}}}{{{{\left( {3!} \right)}^2}{2^6}}}...)\theta {\rm{d}}\theta {\text{，}}\!\! $

(12)

由于相位函数的定义，可得到 $\int_0^\text{ }\!\!\pi\!\!\text{ } {p\left( \theta \right)} \theta {\rm d}\theta {\rm{ = }}\frac{1}{{2\text{ }\!\!\pi\!\!\text{ } }}$ ，上式简化为：

$\begin{array}{l} P(v) = 1 - \frac{1}{4} * 2\text{ }\!\!\pi\!\!\text{ } \int_0^\pi {p\left( \theta \right)} {\theta ^3}{\rm d}\theta {v^2} + \\ \qquad\quad frac{1}{{64}}*2\text{ }\!\!\pi\!\!\text{ } \int\limits_0^\text{ }\!\!\pi\!\!\text{ } {p\left( \theta \right)} {\theta ^5}d\theta {v^4}...{\text{。}} \end{array}$

(13)

采用小角度近似表达式，令 $A=2\text{ }\!\!\pi\!\!\text{ } \int_{0}^{\text{ }\!\!\pi\!\!\text{ } }{p\left( \theta \right)}{{\theta }^{3}}{\rm d}\theta $ ，体散射函数可近似表达为：

$P(v)=1-\frac{1}{4}*A{{v}^{2}}...{\text{，}}$

(14)

将式（14）代入式（9）中，得到媒介光传输函数，如下式：

$S(v,{{z}_{r}})=\exp -(c{{z}_{r}}-b{{z}_{r}}+\frac{1}{12}b{{v}^{2}}{{z}_{r}}^{3}A){\text{。}}$

(15)

2.3 光束传播函数（BSF）

将式（8）、式（15）代入式（5），求得高斯光源的BSF为:

$\begin{array}{l} BSF(r,{z_r}) = \frac{{{P_0}}}{{4\pi \left( {\frac{{{V_0}({z_r})}}{2}{\rm{ + }}\frac{1}{{12}}b{z_r}^3A} \right)}}{e^{ - a}}^{{z_r}} \times \\ \Bigg(1 - \displaystyle\frac{{{r^2}}}{{4\left( {\frac{{{V_0}({z_r})}}{2}{\rm{ + }}\frac{1}{{12}}b{z_r}^3A} \right)}} + \frac{{{r^4}}}{{32{{\left( {\frac{{{V_0}({z_r})}}{2}{\rm{ + }}\frac{1}{{12}}b{z_r}^3A} \right)}^2}}} - \\ \displaystyle\frac{{{r^6}}}{{384{{\left( {\frac{{{V_0}({z_r})}}{2}{\rm{ + }}\frac{1}{{12}}b{z_r}^3A} \right)}^3}}}...\Bigg)\,\, {\text {，}} \end{array}$

(16)

根据马克劳林公式， ${{e}^{-z}}=1-z+\displaystyle\frac{{{z}^{2}}}{2!}-\displaystyle\frac{{{z}^{3}}}{3!}...$ ，可知：

$\begin{array}{l} (1 - \displaystyle\frac{{{r^2}}}{{4\left( {\frac{{{V_0}({z_r})}}{2}{\rm{ \!\!+\!\! }}\frac{1}{{12}}b{z_r}^3A} \right)}} + \frac{{{r^4}}}{{32{{\left( {\frac{{{V_0}({z_r})}}{2}{\rm{ + }}\frac{1}{{12}}b{z_r}^3A} \right)}^2}}} \!\!-\!\! \\[18pt] \quad\quad\displaystyle\frac{{{r^6}}}{{384{{\left( {\frac{{{V_0}({z_r})}}{2}{\rm{ + }}\frac{1}{{12}}b{z_r}^3A} \right)}^3}}}\!\!...) \!\!=\!\! {e^{ - \frac{{{r^2}}}{{4\left( {\frac{{{V_0}({z_r})}}{2}{\rm{ + }}\frac{1}{{12}}b{z_r}^3A} \right)}}}}{\text{。}}\!\! \end{array}$

(17)

将式（17）代入式（16），得到高斯光源的BSF：

$\!BS\!F\!(\!r,{z_r}) \!\!=\!\!\! \frac{{{P_0}}}{{4\pi \!\!\left( {\frac{{{V_0}({z_r})}}{2}{\rm{\! +\! }}\frac{1}{{12}}b{z_r}^3A}\!\! \right)\!}}\!{e^{ - a}}^{{z_r}}{e\!\!^{ - \frac{{{r^2}}}{{4(\frac{{{V_0}({z_r})}}{2}{\rm{ \!+\! }}\frac{1}{{12}}b{z_r}^3A)}}}}{\text{。}}\!\!$

(18)

高斯光源的BSF如上式所示， ${{e}^{-a{{z}_{r}}}}$ 为吸收损耗， $\frac{{{e}^{-\frac{{{r}^{2}}}{4(\frac{{{V}_{0}}({{z}_{r}})}{2}\text{+}\frac{1}{12}b{{z}_{r}}^{3}A)}}}}{4\text{ }\!\!\pi\!\!\text{ } \left( \frac{{{V}_{0}}({{z}_{r}})}{2}\text{+}\frac{1}{12}b{{z}_{r}}^{3}A \right)}$ 是散射造成的损耗，高斯光源的BSF是关于吸收因子、散射因子、相位函数及传输距离的函数。高斯光源的BSF亦为高斯形式，这符合线性系统特性，即输入过程是高斯性，则输出过程也是高斯型^[9]。

3 仿真实验分析

对高斯光源的BSF进行仿真建模，通过开展多种不同叶绿素浓度、传输距离的组合实验，研究分析光功率分布特性，实验结果如图 5所示。

1）分析图 5（a）可知，在相同叶绿素浓度下，光束传输距离越远，接收端的光功率分布强度越小、分布范围越大。强度变小是受吸收、散射等衰减作用影响；范围变大则是随着距离的增加，光子发生散射的机会增多，导致偏离光轴的光子增加，可接收范围增大。

2）通过对比图 5（a）和5（d）可知，在相同的通信距离上，叶绿素浓度的越高，接收端的光功率强度越小。当叶绿素浓度增加到临界值时，光功率强度将为0，通信无法达成。而通信距离越远，其接收端的光强对叶绿素浓度变化越敏感。

3）在相同水质条件下，光斑半径越小时，光功率强度越大。反映在光束的横截面上即为：光斑中间点强度最大，周围距离越远强度越小。

4 结语

相对以往光学信道模型包含繁杂的变量，本文建立了将各物质的浓度转化为叶绿素浓度进行计算的生物光学模型。通过使用汉克尔变换，综合已有的生物光学模型，建立了研究海水信道空间特性的模型。该模型相对传统的比尔定律，关注了终端的功率分布情况，更加精确；相对蒙特卡罗方法，在计算时间和内存要求上，更为简单便捷。实现对不同海域光束的衰减进行预测，在工程实践上有一定参考意义。