2. 哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001
2. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
多址干扰(MAI)一直是困扰CDMA系统多用户发展的主要原因[1]。多用户检测(MUD)技术把所有的用户都当成有用信号来处理,而不是当成干扰来消除,这样可以有效地消除MAI并提高系统容量[2]。2002年,李坪等[3]提出了IDMA技术,有别于其他技术IDMA采用不同的交织器来区分用户,引起了人们的广泛关注。IDMA可以看作是一种特殊形式的CDMA,满足多用户同享频谱资源的要求[4]。而1993年,Turbo码的出现不仅提出了一种编译码方式,更重要的是提供了一种迭代思想[5-7]。通过在发送端进行纠错码编码从而在接收端反馈纠错信息,这就是迭代的中心思想[8]。后来,人们将IDMA与迭代思想相结合,出现了基于IDMA的迭代均衡器[9-11]。由于水下声信道具有未知性和时变性,故结合自适应均衡算法估计信道从而进行MUD[12]。
1 基本理论 1.1 自适应均衡算法自适应信道估计滤波器结构的结构与横向滤波器结构类似。自适应算法通过不断改变滤波器的抽头响应权值向量,进而使滤波器的估计值输出接近于真实信道输出。FIR滤波器的输出为[12]
| $ \hat z\left( n \right) = \sum\limits_{m = 0}^{M - 1} {{{\hat h}_m}\left( n \right){{\tilde x}_{n - m}}} = {{\boldsymbol{\hat h}}^{\rm T}}\left( n \right){{\boldsymbol{\tilde x}}_n}\text{。} $ | (1) |
其中,
基于MMSE理论,其代价函数可以表示为[12]
| $ \begin{split} {J_{\min }}\left( n \right) = E\left\{ {{{\left| {e\left( n \right)} \right|}^2}} \right\} =\\ {\kern 1pt} E\left\{ {{{\left| {z\left( n \right) - {{{\boldsymbol{\hat h}}}^{\rm T}}\left( n \right){{{\boldsymbol{\tilde x}}}_n}} \right|}^2}} \right\}=\\ {\kern 1pt} E\left\{ {{{\left| {z\left( n \right)} \right|}^2}} \right\} - 2{{{\boldsymbol{\hat h}}}^{\rm T}}\left( n \right)E\left\{ {z\left( n \right){{{\boldsymbol{\tilde x}}}_n}} \right\}{\kern 1pt} +\\ \,\,\,\,\,\,\,\, {{{\boldsymbol{\hat h}}}^{\rm T}}\left( n \right)E\left\{ {{{{\boldsymbol{\tilde x}}}_n}{{{\boldsymbol{\tilde x}}}^{\rm T}}_n} \right\}{\boldsymbol{\hat h}}\left( n \right)\text{。} \end{split} $ | (2) |
由于假设发送信息满足同向均匀分布,故
| $ {J_{\min }}\left( n \right) = {{\boldsymbol{C}}_{zz}}\left( n \right) - 2{{\boldsymbol{\hat h}}^{\rm T}}\left( n \right)\theta \left( n \right) + {{\boldsymbol{\hat h}}^{\rm T}}\left( n \right)\Phi \left( n \right){\boldsymbol{\hat h}}\left( n \right)\text{,} $ | (3) |
其中,
| $ \theta \left( n \right) = E\left\{ {z\left( n \right)\tilde x_n^{\rm T}} \right\}\text{,} $ | (4) |
输入与输出的互相关矩阵为[12]
| $ \theta \left( n \right) = E\left\{ {z\left( n \right)\tilde x_n^{\rm T}} \right\}\text{。} $ | (5) |
利用最小梯度算法,得到[12]
| $ \nabla \left| {_{{\bf{\hat h}}\left( n \right)}{J_{\min }}\left( n \right) = - 2\theta \left( n \right) + 2} \right.\Phi \left( n \right){\boldsymbol{\hat h}}\left( n \right) = 0\text{,} $ | (6) |
因此,最佳信道估计抽头权值向量为[12]:
| $ {{\boldsymbol{\hat h}}_{opt}}\left( n \right) = {\varPhi ^{ - 1}}\left( n \right)\theta \left( n \right)\text{。} $ | (7) |
结合RLS算法可见,MMSE算法即是当遗忘因子为1时的特殊情况。此时,对应于系统为无限记忆系统。从而使得工作在非平稳状态下时,对信道的跟踪能力较弱。故引入遗忘因子后可得出最佳信道估计抽头权值向量为:
| $ {{\boldsymbol{\hat h}}_{opt}}\left( n \right) = {\varPhi ^{ - 1}}\left( n \right)\theta \left( n \right)\text{,} $ | (8) |
其中,
| $ \varPhi \left( n \right) = \sum\limits_{i = 1}^n {{\lambda ^{n - i}}{{\tilde x}_n}\tilde x_n^{\rm{T}}} = \lambda \varPhi \left( {n - 1} \right) + {\tilde x_n}\tilde x_n^{\rm{T}}\text{,} $ | (9) |
| $ \theta \left( n \right) = \sum\limits_{i = 1}^n {{\lambda ^{n - i}}{{{\boldsymbol{\tilde x}}}_n}z\left( n \right)} = \lambda \theta \left( {n - 1} \right) + {{\boldsymbol{\tilde x}}_n}z\left( n \right)\text{。} $ | (10) |
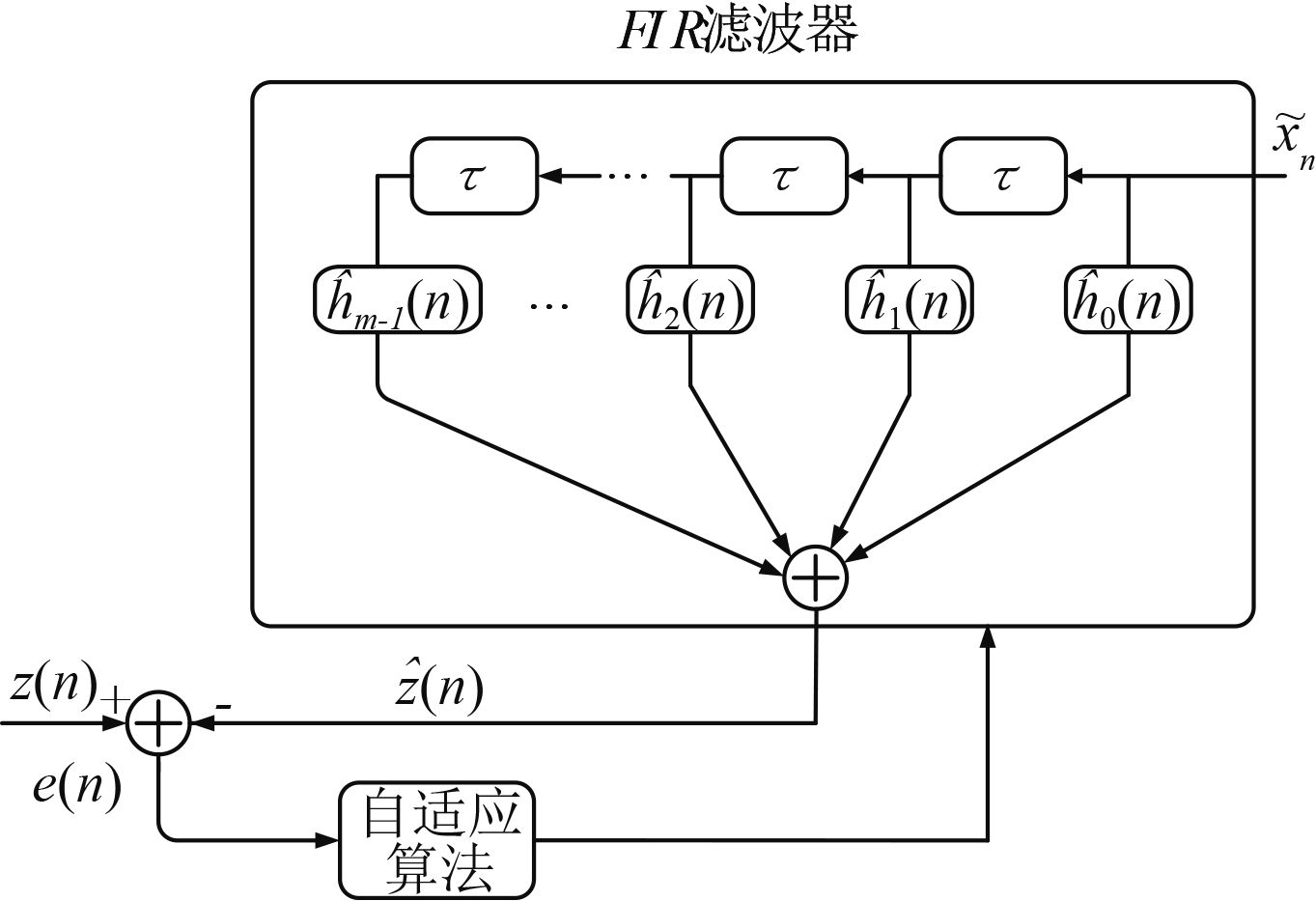
根据上述过程得到如图 1所示。此为有限长单位脉冲响应自适应横向滤波器结构图。自适应滤波器包含2个基本过程:滤波过程和自适应过程。滤波过程计算输入对输入信号的响应并比较输出结果与标准过程的误差;自适应过程根据误差调整滤波器参数。
|
图 1 信道估计滤波器结构图 Fig. 1 Channel estimation filter structure |
信源产生用户原始发送信息
|
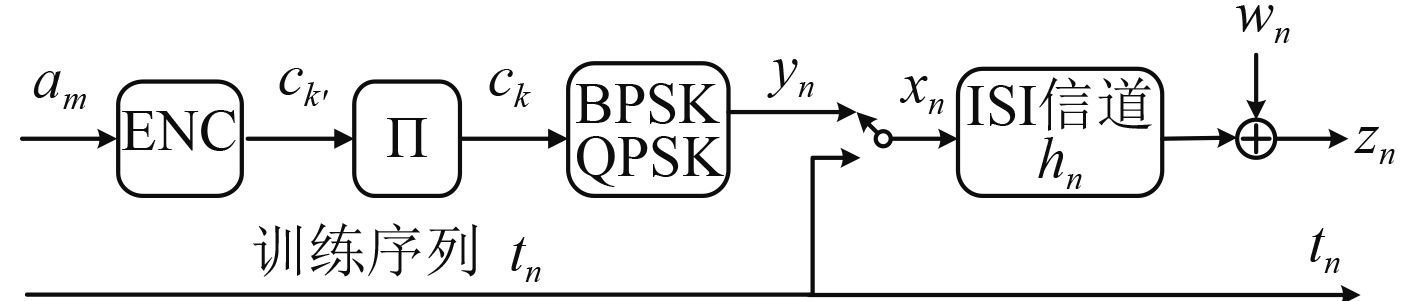
图 2 单用户IDMA发射模型 Fig. 2 Model of IDMA transmitter for single-user |
假设本章中所有滤波器的冲击响应的长度为M,定义长度为M的输入向量
x
n
为
| $ {z_n} = \sum\limits_{i = 0}^{M - 1} {{h_{n,i}}{x_{n - i}}} + {w_n} = {\boldsymbol{h}}_n^{\rm T}{{\boldsymbol{x}}_n} + {w_n}\text{,} $ | (11) |
式中:wn
为高斯噪声,其均值为0,方差为
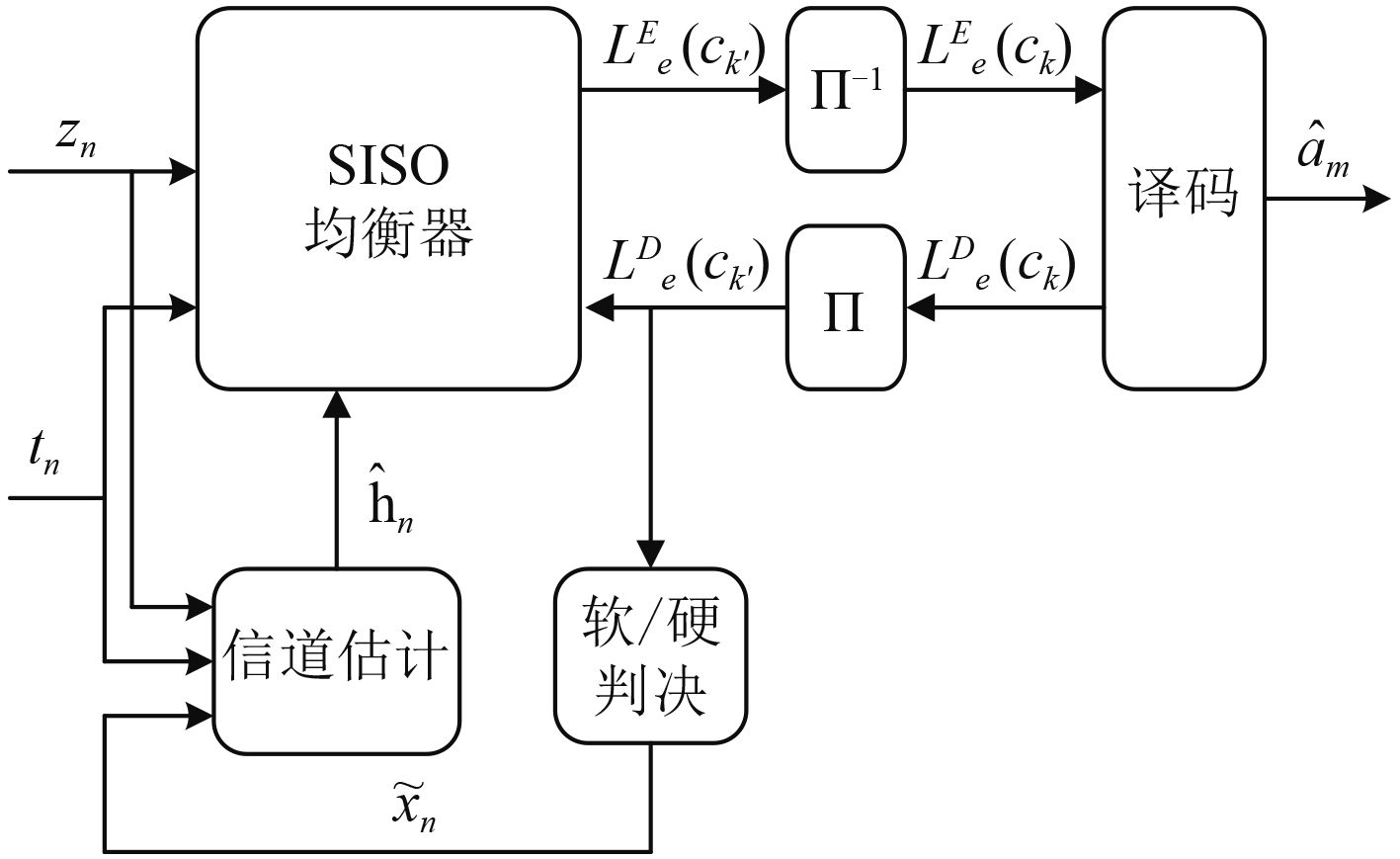
接收机的工作过程为:从接收信号中分离接收到的训练序列,通过与发送端训练序列对比从而计算得到粗略的信道估计值,并送入SISO均衡器;SISO均衡器利用估计的信道参数消除ISI,输出均衡后的均衡器外信息
图 3中的软/硬判决器执行的功能可被分为2部分描述。由前所述可知
|
图 3 单用户自适应Turbo接收机模型 Fig. 3 Model of adaptive turbo receiver for single-user |
| $ L_e^D\left( {{c_k}} \right) = \ln \frac{{P\left( {{c_k} = + 1} \right)}}{{P\left( {{c_k} = - 1} \right)}}\text{,} $ | (12) |
从而可得
| $ P\left( {x = a} \right) = \frac{{{e^{a{\kern 1pt} {\kern 1pt} L_e^D\left( {{c_k}} \right)}}}}{{1 + {e^{a{\kern 1pt} {\kern 1pt} L_e^D\left( {{c_k}} \right)}}}}\text{,}\;\;\;\;\;a \in \left\{ { + 1, - 1} \right\}\text{。} $ | (13) |
当采用BPSK时,软判决计算过程为:计算均值
| $ {c_k} = \left\{ {\begin{array}{*{20}{c}} { + 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} L_e^D\left( {{c_{k'}}} \right) > 0}\\ { - 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} L_e^D\left( {{c_{k'}}} \right) > 0} \end{array}} \right.,\;从而映射成{\tilde x_n}. $ |
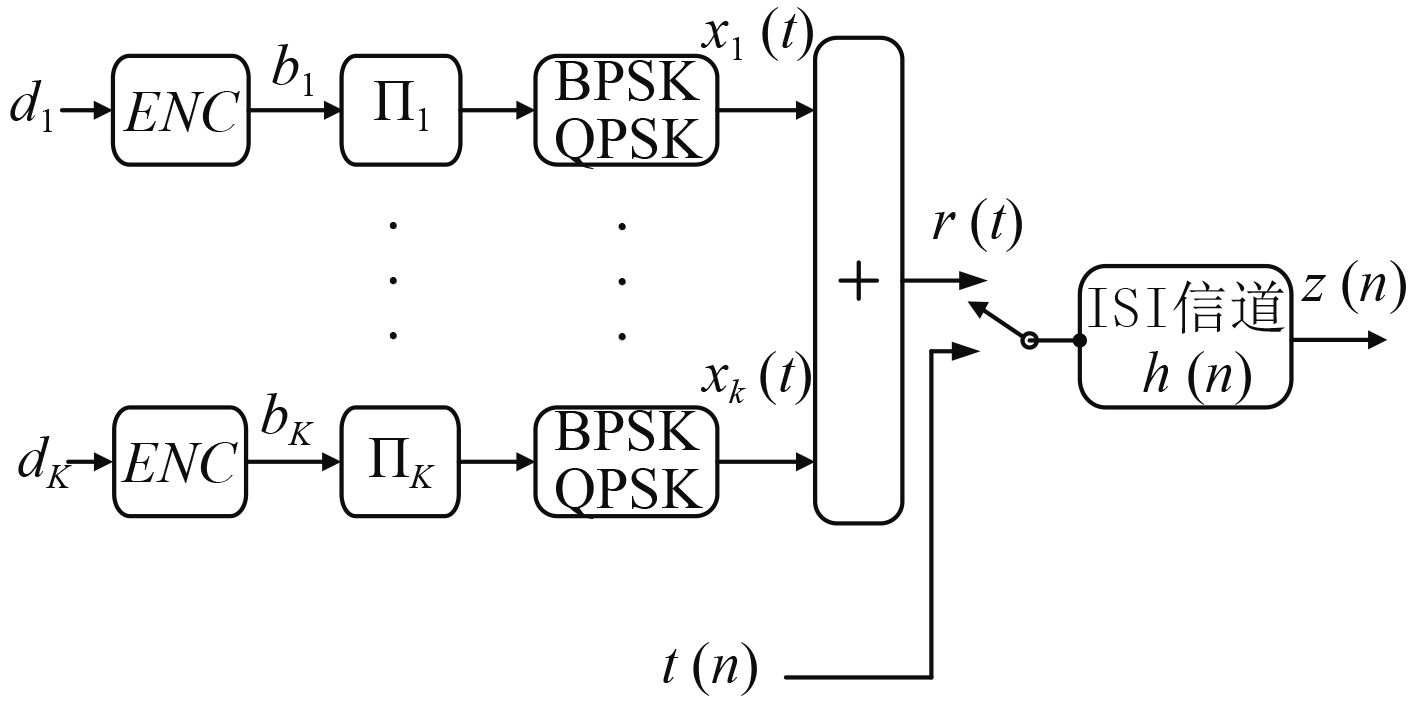
假设系统中含有K个用户,每个用户所发送的数据均采用卷积码编码。编码后的序列经过用户独特的交织器经行交织,从而起到区分用户和减小区域错误对发送数据带来的影响,经交织后的序列采用BPSK或者QPSK调制。本文主要研究下联多用户接收系统,故假设系统完美同步,所以在发送端对多用户发送数据加同一训练序列tn 发送至信道。综上,IDMA多用户系统发射框图如图 4所示。
|
图 4 多用户IDMA发射模型 Fig. 4 Model of IDMA transmitter for multi-user |
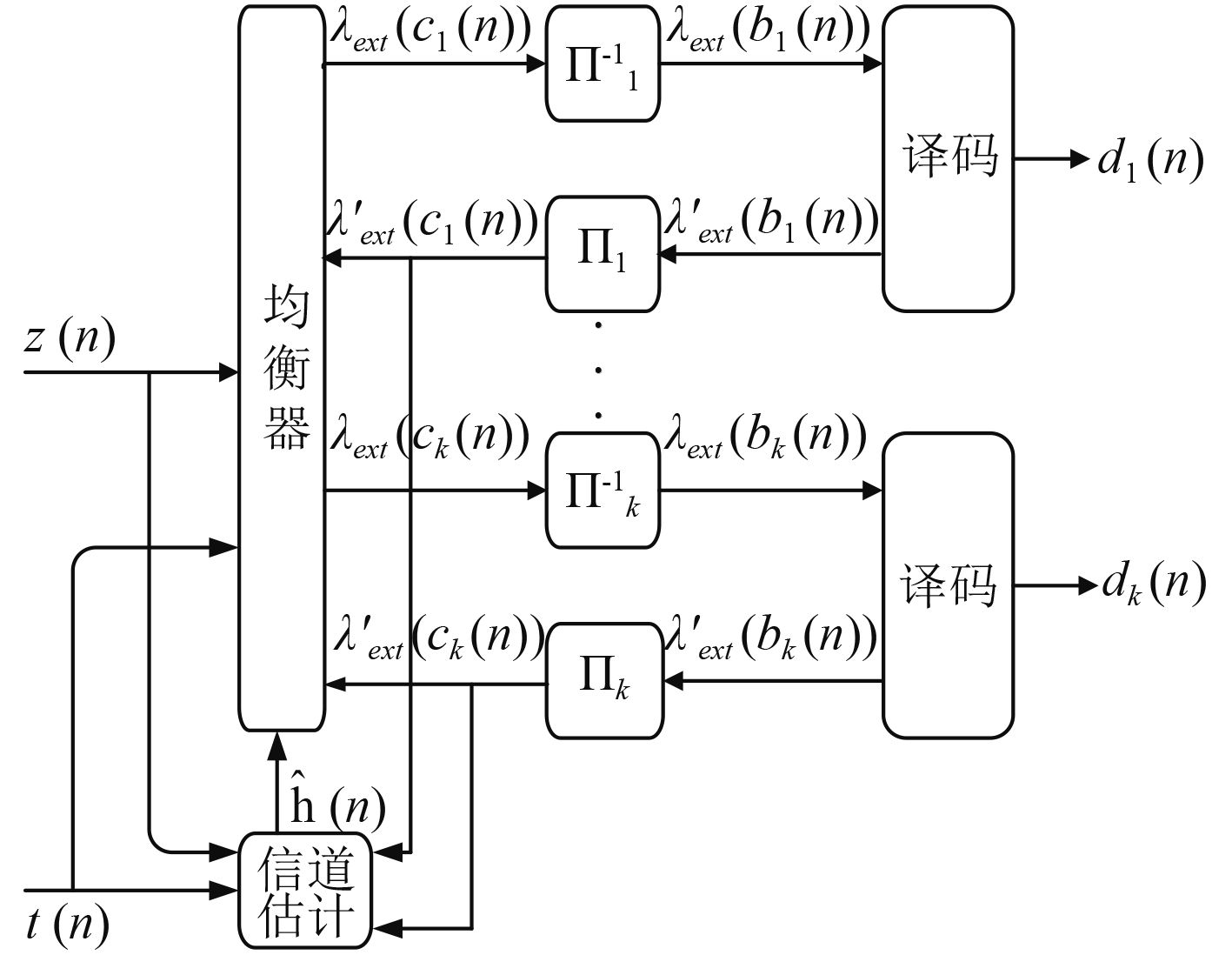
在接收端,接收机首先接收到发送信号的训练序列而后才是多用户发送的数据信息。在接收机中包含训练序列的信息,即用训练序列对信道进行初步的粗估计。将粗估计的信道参数送入均衡器对多用户信息进行均衡。将均衡后的
|
图 5 多用户自适应Turbo接收机模型 Fig. 5 Model of adaptive turbo receiver for multi-user |
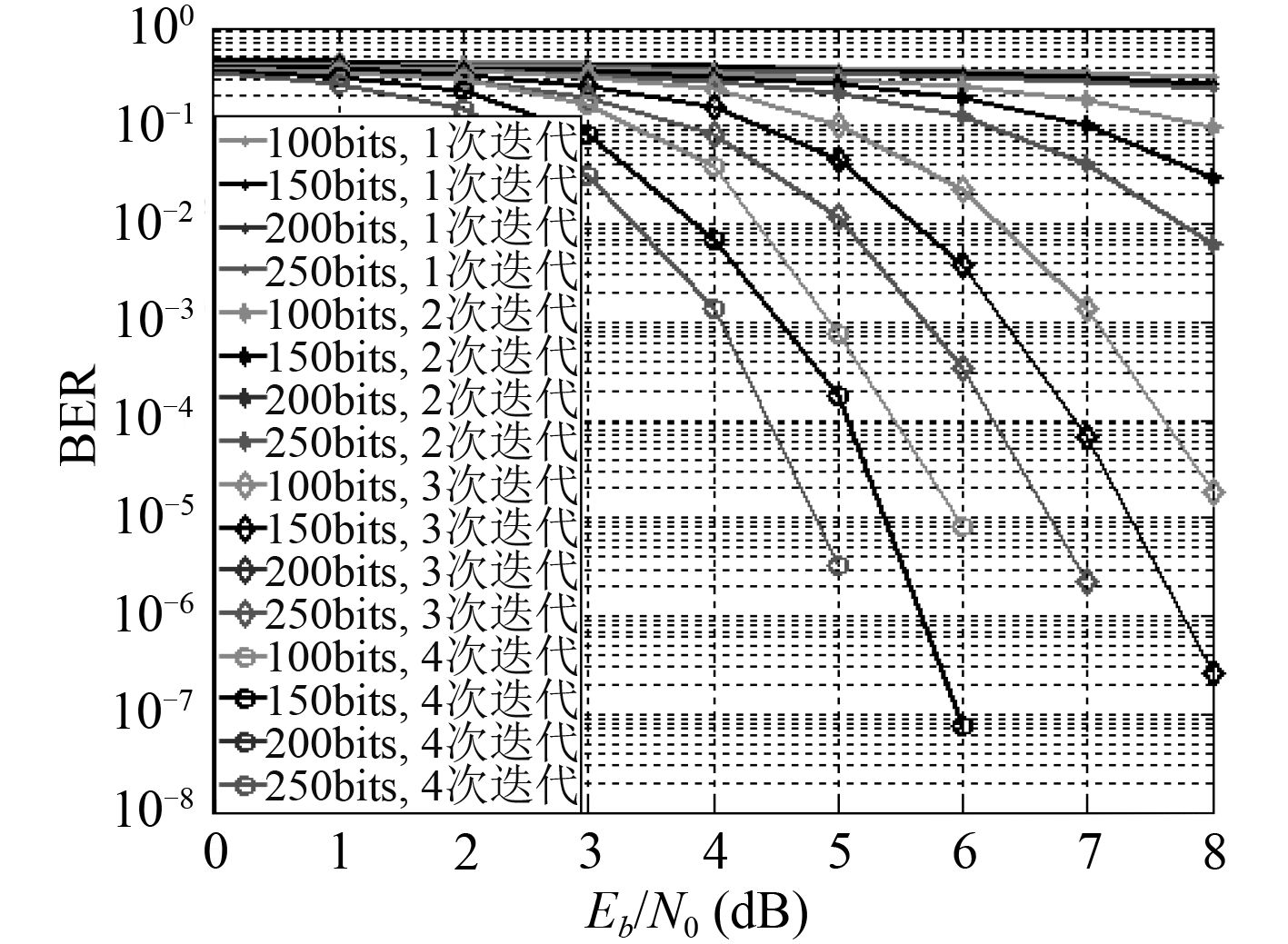
基于IDMA系统,对数据进行卷积码编码,并采用QPSK调制,对信道进行估计。研究训练序长度对系统的影响。如图 6所示。
|
图 6 训练序列长度的影响 Fig. 6 Effect of training sequence length |
从图中可以看出,训练序列长度为200 bits和250 bits时,系统性能不变;在训练序列小于200 bits时,随着训练序列的长度增加,系统性能也逐渐变好。故当训练序列达到一定长度时候,系统性能不变。所以,后续仿真时,训练序列长度选为200 bits。
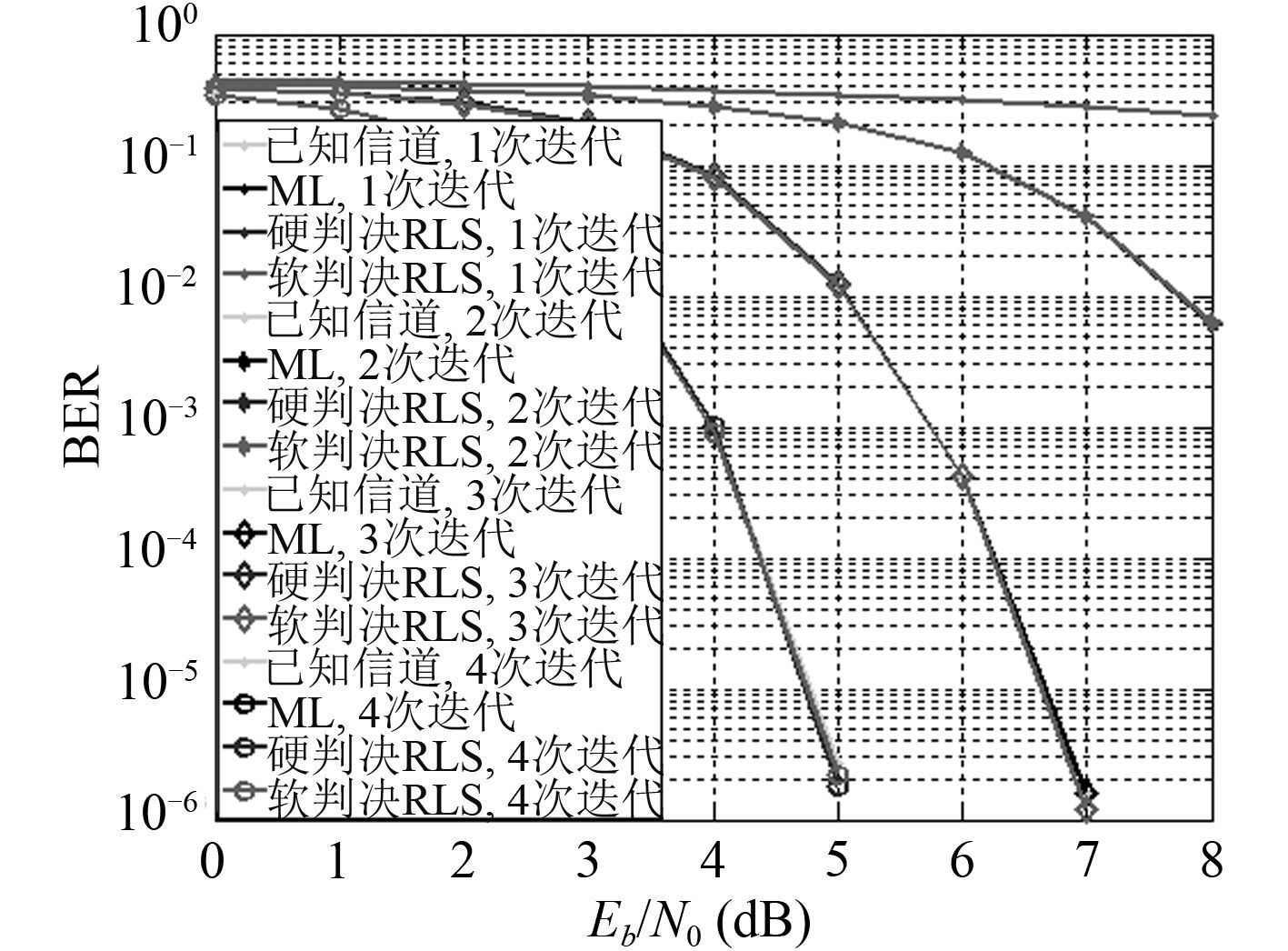
基于IDMA系统,对信源采用卷积码编码,采用QPSK调制。对时不变信道仿真,分析无迭代MMSE估计、结合MMSE和RLS硬判决迭代估计算法和结合MMSE和RLS软信息迭代估计算法系统性能,仿真如图 7所示。
|
图 7 不同信道估计方法系统性能比较 Fig. 7 Performance comparison of different channel estimation methods |
从仿真图中可以看出,当信道为时不变信道时,估计算法的系统性能与已知信道抽头权值向量系统性能相近。证明利用该训练序列和迭代信道估计可以给出置信信道的估计值,使得接收机可以根据该估计值进行均衡检测和译码操作。
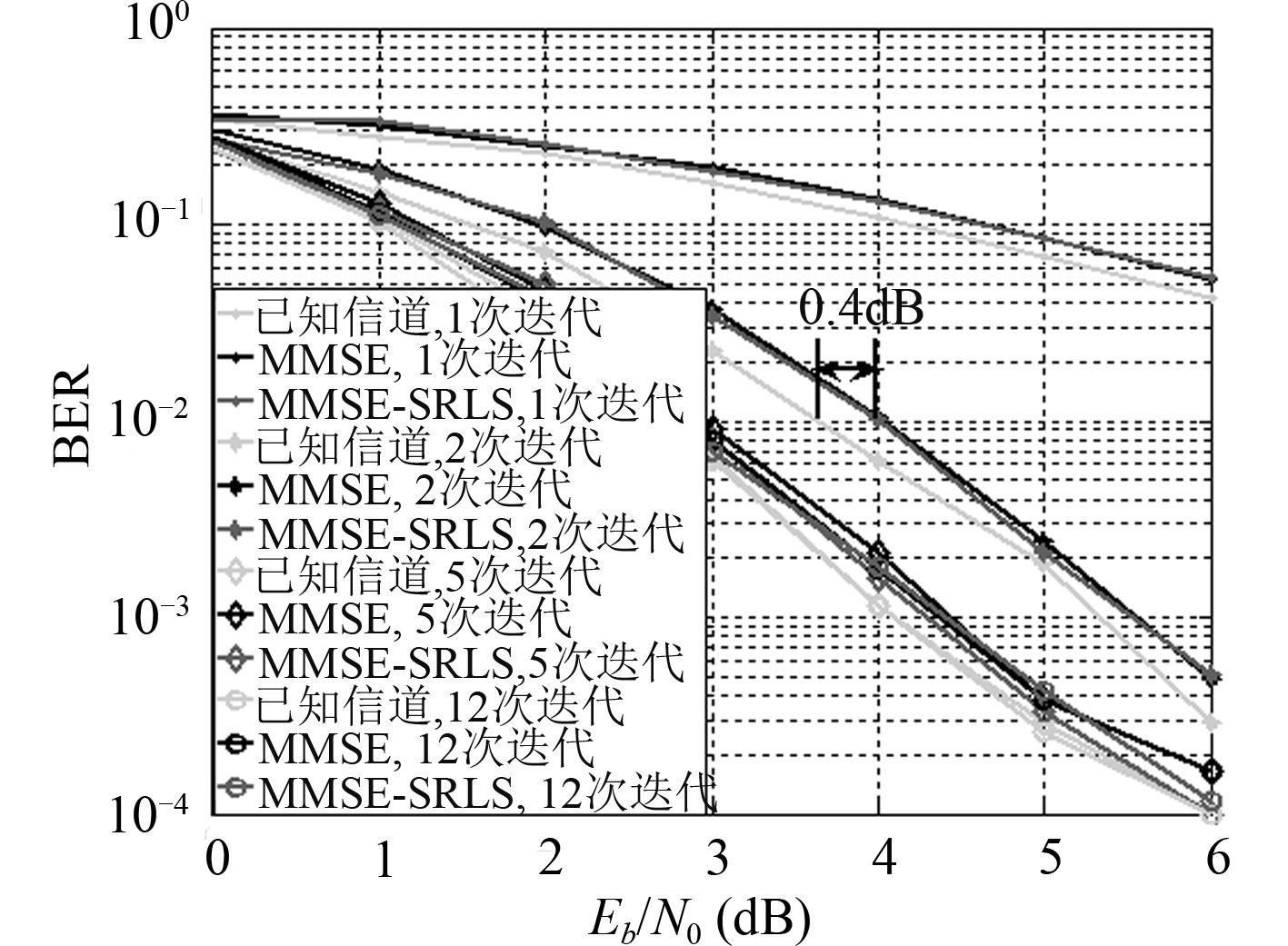
3.2 多用户系统仿真分析基于IDMA系统,对2用户的发送信息进行卷积编码,采用BPSK调制,在发送数据前叠加长度为200 bits的训练序列。研究MMSE信道估计算法和联合MMSE和RLS软判决信道估计算法的系统性能,仿真结果如图 8所示。
|
图 8 多用户迭代信道估计系统性能分析 Fig. 8 Performance analysis of multi-user iterative channel estimation system |
从图中可以看出,2种信道估计算法在时不变信道条件下其系统性能相近;随着接收机迭代次数的增加,BER随之降低。当接收机迭代次数大于5次时,系统性能随着迭代次数的增加不再变化;当BER为10-2时,在第2次迭代条件下,自适应信道估计系统比已知信道系统性能下降0.4 dB。证明了该自适应均衡算法可以很好的用于多用户系统中,计算估计出系统中各个用户信道抽头权值向量的估计值,从而指导接收机工作。
4 结语通过对MMSE信道估计算法的推导得出,该算法可以在未知信道初值的条件下对信道进行估计;而RLS算法需要设定信道的初值从而进行迭代估计。通过对单用户仿真分析得到,在时不变的信道条件下,单独采用MMSE算法估计信道和采用MMSE算法联合RLS算法的软判决迭代信道估计和硬判决迭代信道估计的系统性能相近。通过对训练序列长度的仿真得出,当训练序列达到一定长度后,自适应估计算法不再改善信道的估计值,从而系统性能不变。将自适应信道估计算法应用于多用户IDMA迭代接收系统中,通过仿真结果验证了自适应估计算法能够通过迭代过程利用用户的发送信息进行信道估计,从而改善系统性能。
| [1] | DUEL-HALLEN A, HOLTZMAN J, ZVONAR Z. Multiuser detection for CDMA systems[J]. IEEE Personal Communications , 1995, 2 (2) :46–58. DOI: 10.1109/98.382531 |
| [2] | VERDU S. Multiuser detection[M]. Cambridge: Cambridge University Press, 1998. |
| [3] | PING L, WU K Y, LIU L H, et al. A simple, unified approach to nearly optimal multiuser detection and space-time coding[C]//Proceedings of the Information Theory Workshop. Bangalore, India:IEEE, 2002:53-56. |
| [4] |
胡剑浩, 杨凤, 熊兴中. 交织多址接入系统信道容量证明[J]. 电子科技大学学报 , 2009, 38 (4):481–484.
HU Jian-hao, YANG Feng, XIONG Xing-zhong. Study on the channel capacity for interleave division multiple access systems[J]. Journal of University of Electronic Science and Technology of China , 2009, 38 (4) :481–484. |
| [5] | KOETTER R, SINGER A C, TUCHLER M. Turbo equalization[J]. IEEE Signal Processing Magazine , 2004, 21 (1) :67–80. DOI: 10.1109/MSP.2004.1267050 |
| [6] | TUCHLER M, SINGER A C, KOETTER R. Minimum mean squared error equalization using a priori information[J]. IEEE Transactions on Signal Processing , 2002, 50 (3) :673–683. DOI: 10.1109/78.984761 |
| [7] | TUCHLER M, KOETTER R, SINGER A C. Turbo equalization:Principles and new results[J]. IEEE Transactions on Communications , 2010, 50 (5) :754–767. |
| [8] | TÜCHLER M. Turbo equalization[D]. Munich:Technical University of Munich, 2003. |
| [9] | WU H, PING L, PEROTTI A. User-specific chip-level interleaver design for IDMA systems[J]. Electronics Letters , 2006, 42 (4) :233–234. DOI: 10.1049/el:20063770 |
| [10] | PING L. Interleave-division multiple access and chip-by-chip iterative multi-user detection[J]. IEEE Communications Magazine , 2005, 43 (6) :S19–S23. DOI: 10.1109/MCOM.2005.1452830 |
| [11] | PING L, LIU L H, WU K Y, et al. Interleave division multiple-access[J]. IEEE Transactions on Wireless Communications , 2004, 5 (4) :938–947. |
| [12] | AL-IESAWI S. Adaptive implementation of turbo multi-user detection architecture[J]. Newcastle:University of Newcastle Upon Tyne , 2012 . |
| [13] | OTNES R. Improved receivers for digital High Frequency communications:Iterative channel estimation, equalization, and decoding (adaptive turbo equalization)[D]. Norwegian:Norwegian University of Science and Technology, 2002. |
 2016, Vol. 38
2016, Vol. 38
