2. 哈尔滨工程大学水声工程学院, 黑龙江 哈尔滨 150001
2. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin, 150001, China
近年来,海水中由悬浮泥沙颗粒引起的声吸收成为研究的热点,此类海水也称作混浊海水,例如黄海、长江口以东海域、波斯湾、亚马逊河南大西洋海域、布里斯托尔运河等。国内外声学界曾对混浊海水的声吸收特性进行过仿真分析[1-3]和实验测量[4-5],总结了混浊海水声吸收的一般规律。实验测量一般采用混响法,通过设计不同类型的共振器,测量整个系统的衰减常数,在标定器壁损耗以后,得到混浊海水的声吸收系数。实验研究的关键是设计低器壁损耗、吸声系数小的共振器,例如圆柱形无焊缝铝桶[6]、聚乙烯塑料袋[4, 7]、玻璃瓶[8]等。但是大多数研究只是认为共振器壁与容器内被测混浊海水的声阻抗接近,且器壁外为空气,能形成良好反射,满足混响场条件即可,而没有很好地研究共振器内部的声场特性。这使得所设计共振器的测量误差很大,以至低浓度(悬沙浓度小于0.2 kg/m3)混浊海水的声吸收系数测量值为负值(实际上是不可能的)[4-5],据此实验结果分析低浓度混浊海水的声吸收规律非常困难。本文以圆柱形共振器为例,理论分析其声场,阐明声吸收系数的测量误差如何产生。在此基础上,构建一套声吸收测量系统,以标准溶液(MgSO4)的声吸收系数为研究对象,研究混响时间测量方法所引起的误差大小,以期能对低浓度、低频段混浊海水的声吸收特性研究提供技术支撑。
1 海水声吸收测量方法测量海水声吸收的方法主要有海上直接测量和实验室测量2种[9]。实验室测量海水声吸收系数的精度要比海上直接测量高得多,方法分为行波法、混响法和共振法。行波法适用于1MHz以上频段,而低频段(几十或几百千赫)海水的声吸收系数测量一般采用混响法或共振法。由于海水的声吸收系数是一个小量(如40 kHz时,纯净海水的声吸收系数约为0.008 0 dB/m),因此实验研究的关键是设计一个容积大而器壁附加损耗小的共振器。
共振法原理如下:在充水的共振器中,利用发射换能器尽可能地激发起一个简正波方式。停止激发后,测量出液体及容器边界所决定的衰减常数δs 。边界的影响可通过共振器充以标准液体并激发同一简正波方式时所得的衰减常数δw 来实现。
待测液体的声吸收系数为:
| $ {\alpha _{e1}} = \left( {{\delta _s} - {\delta _w}} \right)/c{\text{。}} $ | (1) |
式中:c为液体介质的声速。混响法原理跟共振法差不多,只是混响法要求共振器在某一频带内激发出大量的简正波方式,使得出现扩散声场,而不是单一的简正波方式。
共振器内声能衰减常数的快慢可用混响时间来描述。当共振器内声源辐射的能量达到稳态后,声源停止发声,残余的声能被共振器边界及其内液体介质吸收,声压级下降60 dB(相当于平均声能密度降为初始值的百万分之一)所需的时间。用符号T60表示[10]:
| $ {T_{60}} = \frac{{55.26V}}{{c(\mathop a\limits^\_ S + 8\alpha V)}}\text{。} $ | (2) |
式中:V为共振器的体积;S为共振器的表面积;
纯水的声速c0和声吸收系数α0能从手册上查得,V,S和共振器充以纯水的T60可测量得到,故式(2)中吸声系数
| $ \alpha = \frac{1}{{{c_0}}}\left( {\frac{{60}}{{T_{60}'}} - \frac{{60}}{{{T_{60}}}}} \right) + {\alpha _0}\text{。} $ | (3) |
式中:α0为纯水的声吸收系数;α为电解质溶液或混浊海水的声吸收系数;c0为纯水的声速;T60为纯水的混响时间;T60′为电解质溶液或混浊海水的混响时间。
2 共振器内的声场特性分析 2.1 共振器内无声源时的声场分析

|
图 1 圆柱形共振器的照片 Fig. 1 Practical photo of cylindrical resonator |
设共振器外半径为R(100.2 cm)、高为H(54 cm)、壁厚为h(0.4 cm),如图 2所示,建立柱面坐标系。
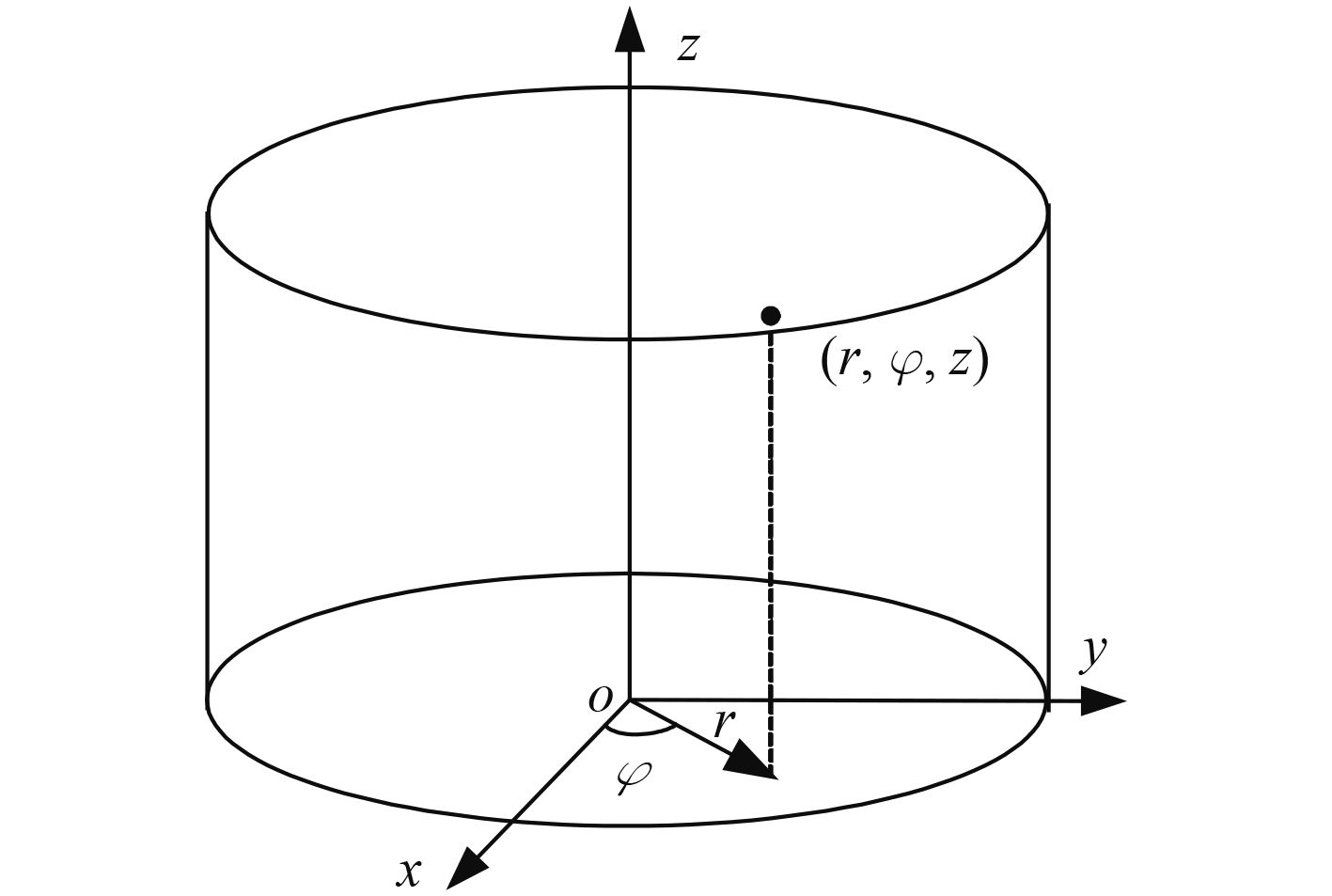
|
图 2 柱面坐标系 Fig. 2 Cylindrical coordinates |
当共振器中没有声源时,声场势函数满足波动方程[11]:
| $ {\nabla ^2}\varPsi + {k^2}\varPsi = 0\text{,} $ | (4) |
应用分离变量法和声压为0的边界条件以及在r=0处声压有限,可求得本征函数为:
| $ \varPsi \!\! =\!\! \sum\limits_{l = 1} {\sum\limits_{m = 0} {\sum\limits_{n = 1} {\begin{array}{*{20}{c}} {{A_{lmn}}\cos }\\ {{B_{lmn}}\sin } \end{array}(m\varphi )\sin \left( {\frac{{l\text{ }\!\!\pi\!\!\text{ } }}{H}z} \right){J_m}\left( {\frac{{{\mu _{mn}}\text{ }\!\!\pi\!\!\text{ } }}{R}r} \right)} } } \text{,}\!\! $ | (5) |
共振频率为:
| $ \left. \begin{array}{l} {f_{lmn}} = \displaystyle\frac{\omega }{{2\text{ }\!\!\pi\!\!\text{ } }} = \frac{c}{2}\sqrt {{{\left( {\displaystyle\frac{l}{H}} \right)}^2} + {{\left( {\displaystyle\frac{{{\mu _{mn}}}}{R}} \right)}^2}} \\[5pt] l = 1,2,3...;m = 0,1,2...;n = 1,2,3... \end{array} \right\}\text{。} $ | (6) |
式中μmn 值为贝塞尔方程Jm (πμmn )=0的根。需要注意的是式(6)没有考虑器壁厚度的影响。
2.2 共振器壁厚、密度特性对声场特性的修正当共振器中的声场达到稳态,形成驻波场以后,声压和振速的相位差为90°。即当声压为最大时,振速为0;当振速为最大时,声压为0。因此,把共振器和所充水当作一个弹性体,则声能密度[11]可写成:
| $ E = \frac{1}{2}\frac{{{p^2}}}{{{\rho _{all}}{c^2}}} + \frac{1}{2}{\rho _{all}}{u^2}\text{。} $ | (7) |
式中:p为声压;u为振速;ρall 为共振器的整体密度;c为液体介质的声速。
因共振器的材料为铝,声阻抗跟水接近,在桶壁处声压为0,而振速最大。当声压为0时,声能密度与材料的密度成正比;当振速为0时,声能密度与共振器的体弹性模量成反比。因此,按照式(7)可对共振器的材料特性进行修正,采用相对密度来表示。共振器的高度和半径可写成如下形式:
| $ \left. \begin{array}{l} {H_e} = H + ({\rho _a}/{\rho _w} - 1)h\\ {R_e} = R + ({\rho _a}/{\rho _w} - 1)h \end{array} \right\}\text{,} $ | (8) |
式中:ρa 为共振器材料(铝)的密度;ρw 为共振器内介质(水)的密度。代入式(5)和式(6)中,即:
| $ \psi {\rm{ = }}\sum\limits_{l = 1} {\sum\limits_{m = 0} {\sum\limits_{n = 1} {_{{B_{lmn}}\sin }^{{A_{lmn}}\cos }} } } \left( {m\varphi } \right)\sin \left( {\frac{{{\rm{l}}\text{ }\!\!\pi\!\!\text{ } }}{{{H_{\rm{e}}}}}z} \right){J_m}\left( {\frac{{{\mu _{mn}\text{ }\!\!\pi\!\!\text{ } }}}{{{R_e}}}r} \right), $ | (9) |
| $ \left. \begin{array}{l} {f_{lmn}} = \frac{\omega }{{2\text{ }\!\!\pi\!\!\text{ } }} = \frac{c}{2}\sqrt {{{\left( {\frac{l}{{{H_e}}}} \right)}^2} + {{\left( {\frac{{{\mu _{mn}}}}{{{R_e}}}} \right)}^2}} \\ l = 1,2,3...;m = 0,1,2...;n = 1,2,3... \end{array} \right\}\text{。} $ | (10) |
式(10)表明:如果He 不大于Re ,那么共振器最低频率的简正模态就是径向振动。通过测量共振器最低的共振模态(如m=0,n=1的方式),则可得到共振器中液体介质的声速。
2.3 共振器中的简正波共振器中的简正波分为以下2类:一是切向波:r,z切向波(m=0);二是斜向波:(l,m,n均不为0)。
采用频率空间里圆的一部分来表示各个波,柱面波是由各个方向前进的平面波组合而成,如图 3所示。
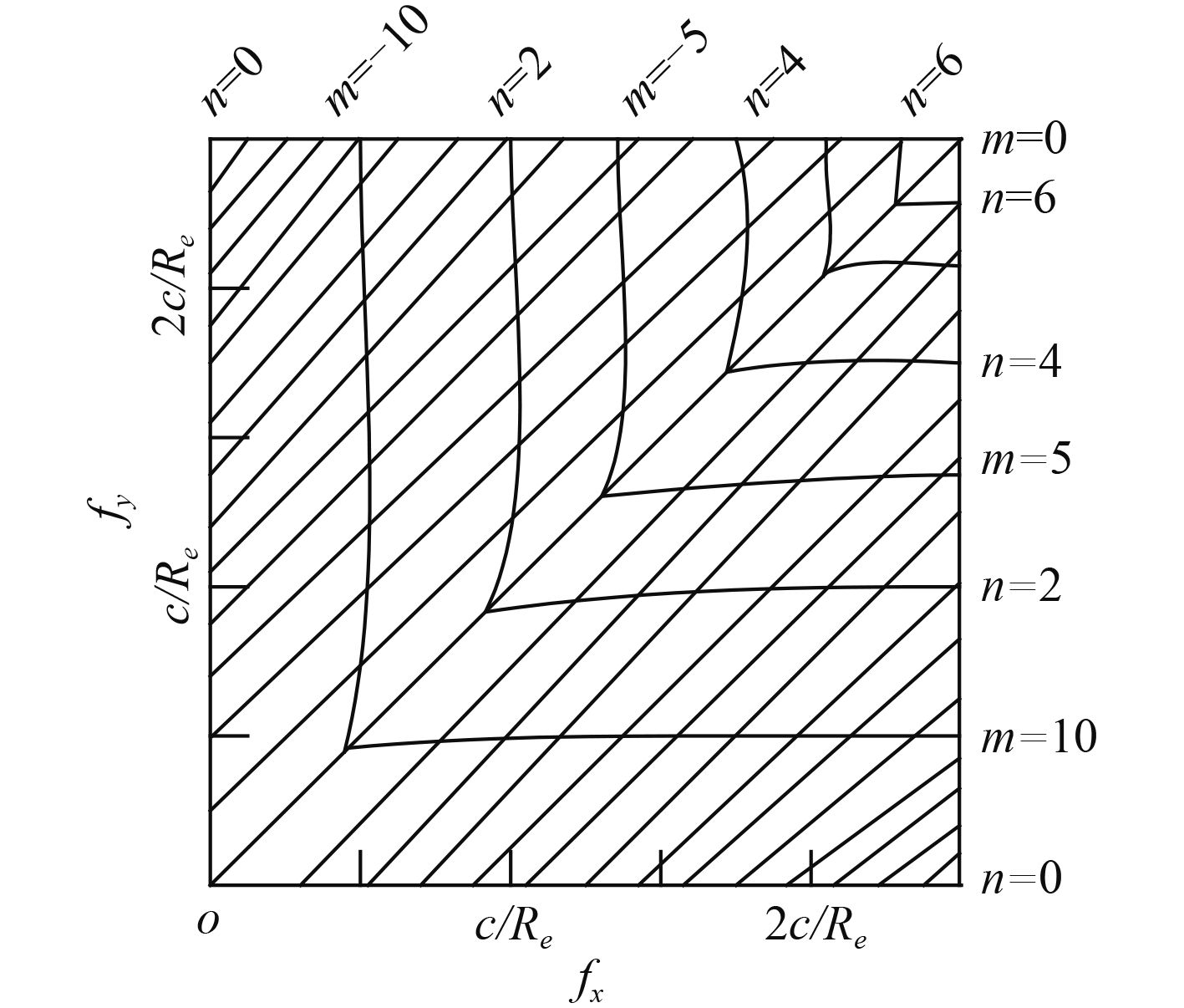
|
图 3 圆柱形共振器中的容许频率 Fig. 3 Nominal representation of allowable frequency in the cylindrical resonator |
| $ {N_{{\text{切}},{{rz}}}} = (2\text{ }\!\!\pi\!\!\text{ } {R_e}{H_e}{{ f}^2}/{c^2}) - f(2\text{ }\!\!\pi\!\!\text{ } {R_e} + {H_e})/c\text{,} $ | (11) |
| $ {N_{\text{斜}}} = (4\text{ }\!\!\pi\!\!\text{ } {f^3}V/3{c^3}) - (\text{ }\!\!\pi\!\!\text{ } S{f^2}/4{c^2}) + (Lf/8c)\text{。} $ | (12) |
式中:
当共振器中受到一个频率为f=ω/2π、强度为Qω 且位于r0上的简单声源激发时,则共振器内声场的势函数满足波动方程:
| $ {\nabla ^2}\varPsi (r) + {k^2}\varPsi (r) = - {Q_\omega }\delta (r - {r_0})\text{,} $ | (13) |
将
| $ \psi \ (r,{r_0}) = - {Q_\omega }\sum\limits_{l = 1} {\sum\limits_{m = 0} {\sum\limits_{n = 1} {\frac{{{\psi \ _{lmn}}({r_0}){\psi \ _{lmn}}(r)}}{{({k^2} - K_{lmn}^2)V{\Lambda _{lmn}}}}} } } \text{。} $ | (14) |
式中:
共振器内任一点的声压为:
| $ p(r,{r_0}) = - i\rho \omega {Q_\omega }\sum\limits_{l = 1} {\sum\limits_{m = 0} {\sum\limits_{n = 1} {\frac{{{\psi \_{lmn}}({r_0}){\psi \ _{lmn}}(r)}}{{({k^2} - K_{lmn}^2)V{\Lambda _{lmn}}}}} } } \text{。} $ | (15) |
由式(15)可知,当共振器的边界和内部介质不存在损耗时,Klmn 为实数。当k=Klmn 时,则式(15)中第lmn项将趋于无穷大,达到共振。由于在实际情况中,边界及内部介质均存在损耗,因此Klmn 为复数
2.5 共振器内的瞬态响应(混响)当激发起共振器内某一简正波方式的声源关掉时,则该驻波按指数规律衰减。阻尼常数γlmn
正比于第lmn个方式在共振器壁上损耗的功率与驻波总能量之间的比值[12]。共振器壁单位面积上损耗的功率是
| $ 2{\gamma _{lmn}} = \frac{{Sc}}{V} \cdot \frac{{\xi {{\left| {\varPsi _{lmn}^2} \right|}_S}}}{{{{\left| {\varPsi _{lmn}^2} \right|}_V}}}\text{。} $ | (16) |
式中:V为体积;S为表面积;
阻尼常数γlmn
可用式(15)中
| $ p(r,t) = \sum\limits_{l = 1} {\sum\limits_{m = 0} {\sum\limits_{n = 1} {{A_{lmn}}{e^{ - {\gamma _{lmn}}t}}\cos ({\omega _{lmn}}t + {\phi _{lmn}})} } } \text{。} $ | (17) |
式中:累加号是对
因此,共振器中声压的均方根值为:
| $ \left\langle {{p^2}} \right\rangle = \sum\limits_{l = 1} {\sum\limits_{m = 0} {\sum\limits_{n = 1} {A_{lmn}^2{{\rm e}^{ - 2{\gamma _{lmn}}t}}} } } \text{,} $ | (18) |
若考虑共振器内液体介质的声吸收时,则上式可写为:
| $ \left\langle {{p^2}} \right\rangle = \left( {\sum\limits_{l = 1} {\sum\limits_{m = 0} {\sum\limits_{n = 1} {A_{lmn}^2{{\rm e}^{ - 2{\gamma _{lmn}}t}}} } } } \right) \cdot {{\rm e}^{ - 2\alpha ct}}\text{。} $ | (19) |
由于
| $ {\mathop a\limits^\_\!{_{\text{斜向}}}} = 8\left[ {\left\langle \xi \right\rangle \pi R_e^2 + \left\langle \xi \right\rangle \pi {R_e}{H_e}} \right]\text{,} $ | (20) |
| $ {\mathop a\limits^\_\!{_{\text{切向}}}} = 8\left[ {\left\langle \xi \right\rangle \pi R_e^2 + \frac{1}{2}\left\langle \xi \right\rangle \pi {R_e}{H_e}} \right]\text{。} $ | (21) |
因此,把式(11)和式(12)计算的共振器内斜向波和切向波数目代入式(19)中,则得到共振器内声波衰减过程中的均方声压为:
| $ \begin{split} \left\langle {{p^2}} \right\rangle = \left[ {\displaystyle\frac{{{k^2}V}}{{2{\text{ }\!\!\pi\!\!\text{ } ^2}}}{e^{ - \displaystyle\frac{{c{{\mathop a\limits^\_ }_{\text{斜向}}}t}}{{4V}}}} - \frac{{kR_e^2}}{4}{e^{ -\displaystyle \frac{{c{{\mathop a\limits^\_ }_{\text{斜向}}}t}}{{4V}}}} + ...+} \right.\\ \begin{array}{*{20}{c}} {} & {\begin{array}{*{20}{c}} {} & {\left. { \displaystyle\frac{{{R_e}{H_e}}}{\text{ }\!\!\pi\!\!\text{ } }{e^{ -\displaystyle \frac{{c{{\mathop a\limits^\_ }_{\text{切向}}}t}}{{4V}}}} + ...} \right]{e^{ - 2\alpha ct}}\left\langle {|{A^2}|} \right\rangle } \end{array}} \end{array}=\\ \begin{array}{*{20}{c}} {} & {} \end{array} {I_0}{D_l}(t){D_m}(t){D_\alpha }(t)\text{,} \end{split} $ | (22) |
式中:
| $\begin{array}{*{35}{l}} {{D}_{l}}(t)={{e}^{-\frac{c{{{\bar{a}}}_{l}}t}{4V}}};\ {{D}_{\alpha }}(t)={{e}^{-2\alpha ct}}, \\ {{D}_{m}}(t)={{e}^{-\frac{c{{{\bar{a}}}_{m}}t}{4V}}}\left[ 1-\frac{kR_{e}^{2}}{4}+...+\frac{{{R}_{e}}{{H}_{e}}}{\text{ }\pi \text{ }}{{e}^{+\frac{c{{\overset{\_}{\mathop{\text{ }a}}\,}_{m}}t}{8V}}}+... \right]。 \\ \end{array}$ |
其中,
由此可知,当一个声源在共振器内突然停止后,共振器内部的声压级衰减曲线(即声压级与时间的对数)是形如
在利用共振器测量液体介质的声吸收时,要考虑到以下诸多实验难点:一是共振器的低吸声设计;二是传感器(发射换能器和水听器)的低声吸收设计;三是共振器的隔声、隔振、保温设计;四是被测介质的除气设计等。
所用共振器为铝桶、无焊逢,大大减少了器壁的损耗,如图 1所示。铝桶内表面喷涂低声损耗的防腐蚀漆,边缘搁置在楔形木块斜面上,并共轴放置在一圆柱形钢桶内,可靠地消除了环境振动对共振器的影响。在钢桶的顶部有抽气、放气、观察窗等设备,能对共振器中的纯水、电解质溶液或混浊海水进行真空除气,以消除气泡对测量结果的影响。在钢桶的外面包裹有3层塑料泡末,并结合房间内的空调保持共振器中液体介质的温度恒定。在发射换能器和水听器的电缆上密缠铝箔纸,以减少电缆引起的声吸收。
这里采用混响法测量液体介质的声吸收系数,系统框图如图 4所示。由数据采集器PULSE分析仪(型号:B & K3560E)中的信号源发射白噪声,信号经过功率放大器(型号:B & K2713)后,加至发射换能器。经5 s之后,信号源停止工作。用水听器(型号:B & K8103)来监视共振器内声压级的衰减,接收的信号经过测量放大器(型号:B & K2692)后,由PULSE分析仪进行采集分析,并给出1/3倍频程中心频率处的混响时间。实验记录的频率为20 kHz,25 kHz,31.5 kHz,40 kHz,50 kHz,63 kHz。采样频率为512 kHz,数据记录长度为15 s。实验过程如下:先在共振器内注入纯水,经真空除气后,测量纯水的混响时间T60;此后在共振器内注入等体积的MgSO4溶液(浓度为0.014 mol/L),测量其混响时间T60′,由式(3)计算MgSO4溶液的声吸收系数。该浓度MgSO4溶液的声吸收系数可按文献中[13]理论公式计算得到。将两者进行对比,以校验所研制系统的测量误差。实验中液体介质的温度为20 ℃。
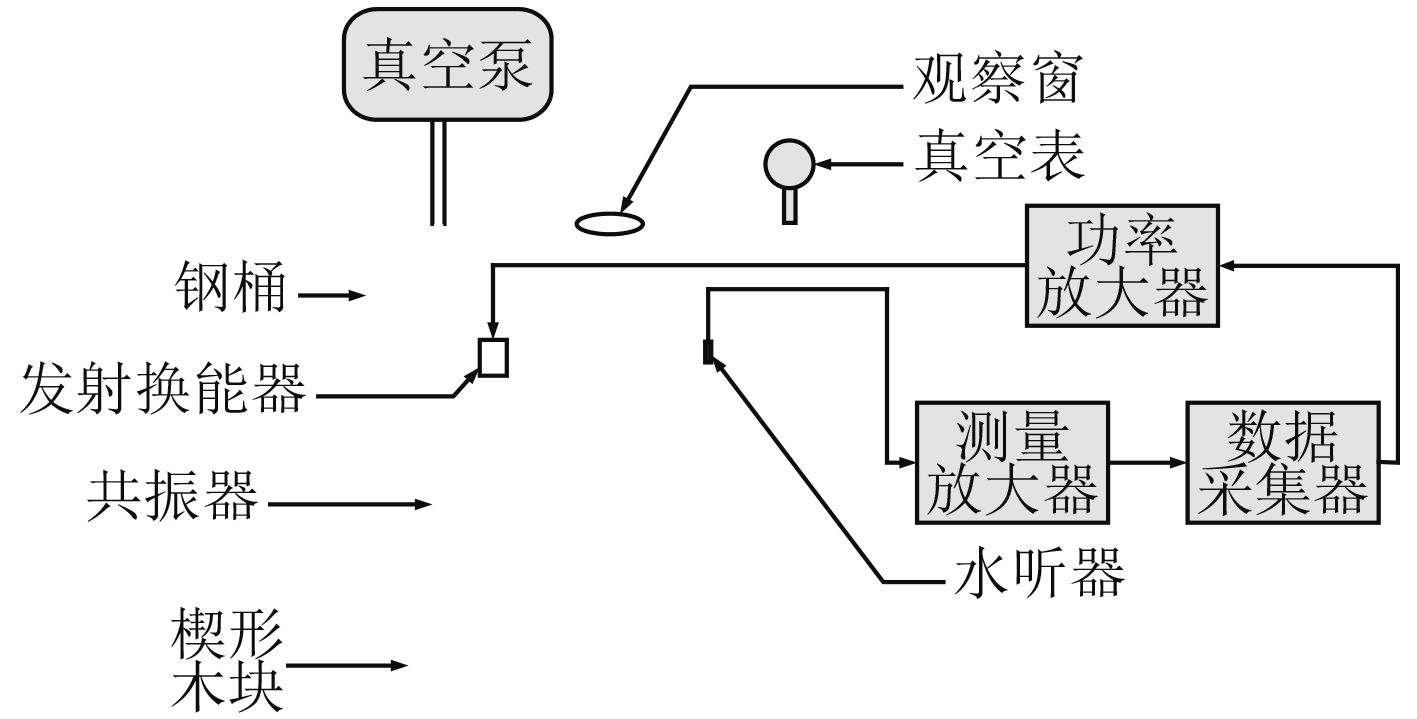
|
图 4 测量系统框图 Fig. 4 Schematic diagram of measurement system |
选用的水听器为柱形,直径0.95 cm,长1.58 cm。发射换能器为柱形,直径约3 cm,长5 cm。经文献[10]中公式计算得到共振器内声源的直达声场和混响声场的临界距离为0.9 cm。在实验中,发射换能器和水听器之间的距离不小于15 cm,以使水听器位于混响声场中。
按文献中[14]铝的性能可知,共振器在充液体后,因液体重力引起的形状变化非常小,因此忽略共振器充液体后的体积变形。这里考察混响时间测量方法不同而导致的声吸收系数测量误差。混响时间测点的示意图如图 5所示,在共振器的水平面内选取18个点,点与点之间距离大于λ/2,测点离共振器边界距离大于λ/2(λ为研究频段中的最大波长),并取离水面5 cm,15 cm,25 cm,35 cm,45 cm共5个深度,依次命名为深度1,2,3,4,5,总计90个空间测点。
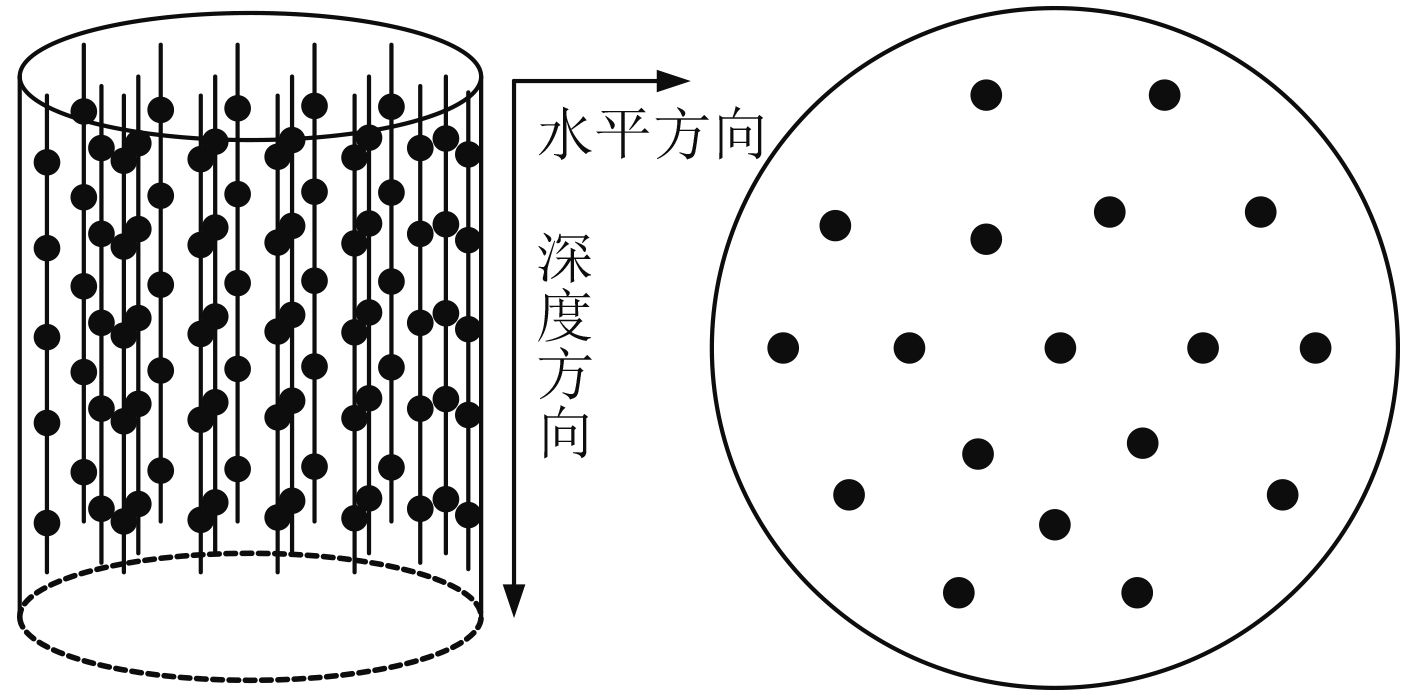
|
图 5 混响时间测点示意图 Fig. 5 Schematic diagram of the reverberation time measurement points |
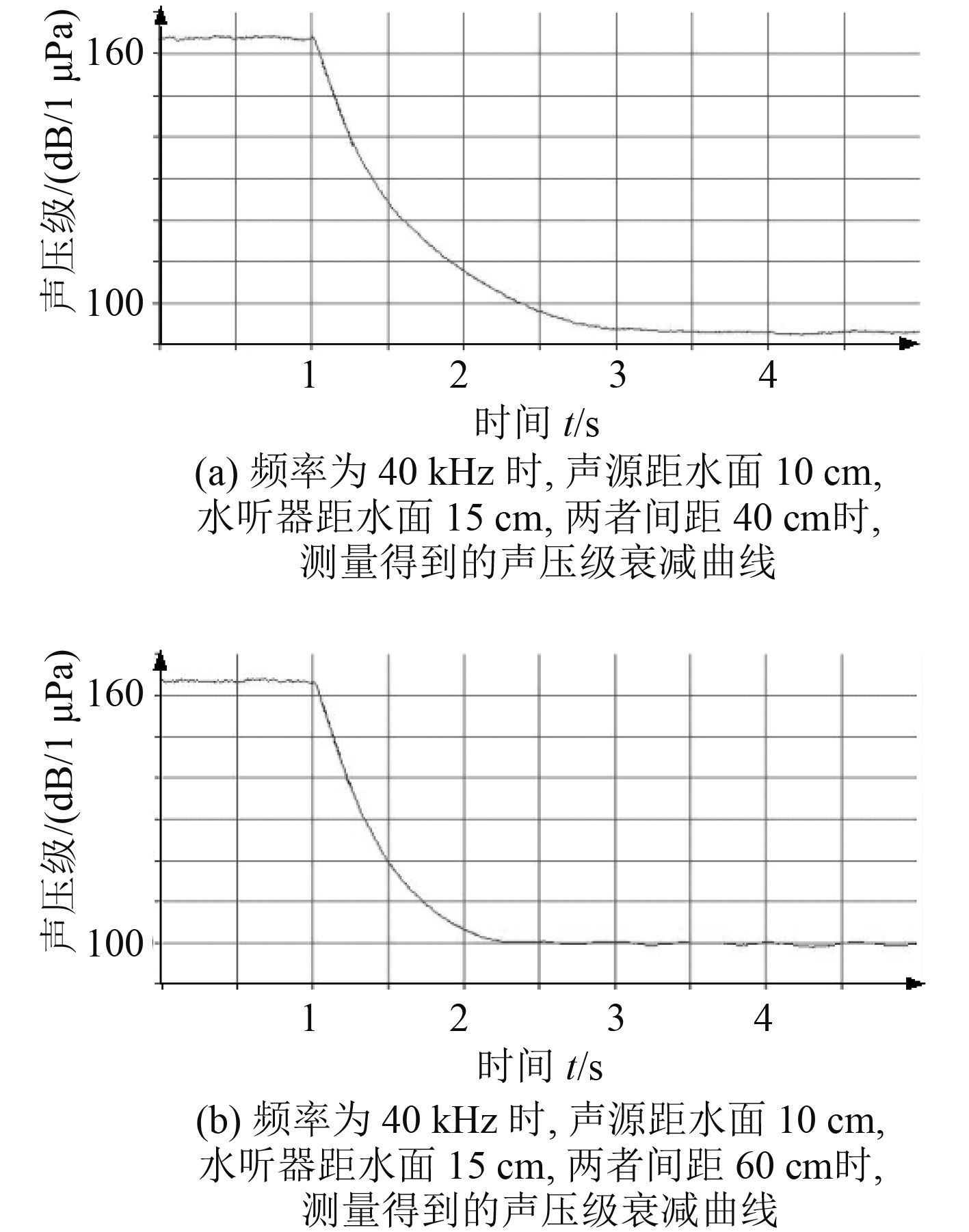
发射换能器和水听器在共振器中同一深度(即传感器电缆引起的声吸收相同)、不同空间位置处测量得到的声压级衰减曲线如图 6所示。这表明:在其他参数确定以后,不同简正模态(切向波、斜向波)l的声压级衰减不一样,由此说明不同空间位置处的声压衰减曲线有区别,后面的实验据此展开。
|
图 6 共振器中同深度、不同空间位置处的声压级衰减曲线 Fig. 6 Decay curves of sound pressure level at the same depth and different spatial locations in the resonator |
设计以下4组实验,以考察不同混响时间测量方法所引起的声吸收系数测量误差:
1)在纯水和MgSO4溶液中选取的混响时间测点位置,在水平方向和深度方向均不相同。
2)在纯水和MgSO4溶液中选取的混响时间测点位置,在水平方向不同而深度方向相同。
3)在纯水和MgSO4溶液中选取的混响时间测点位置,在深度方向相同且对水平方向的测点数据进行平均。
4)在纯水和MgSO4溶液中选取的混响时间测点位置,在水平方向和深度方向均完全相同。
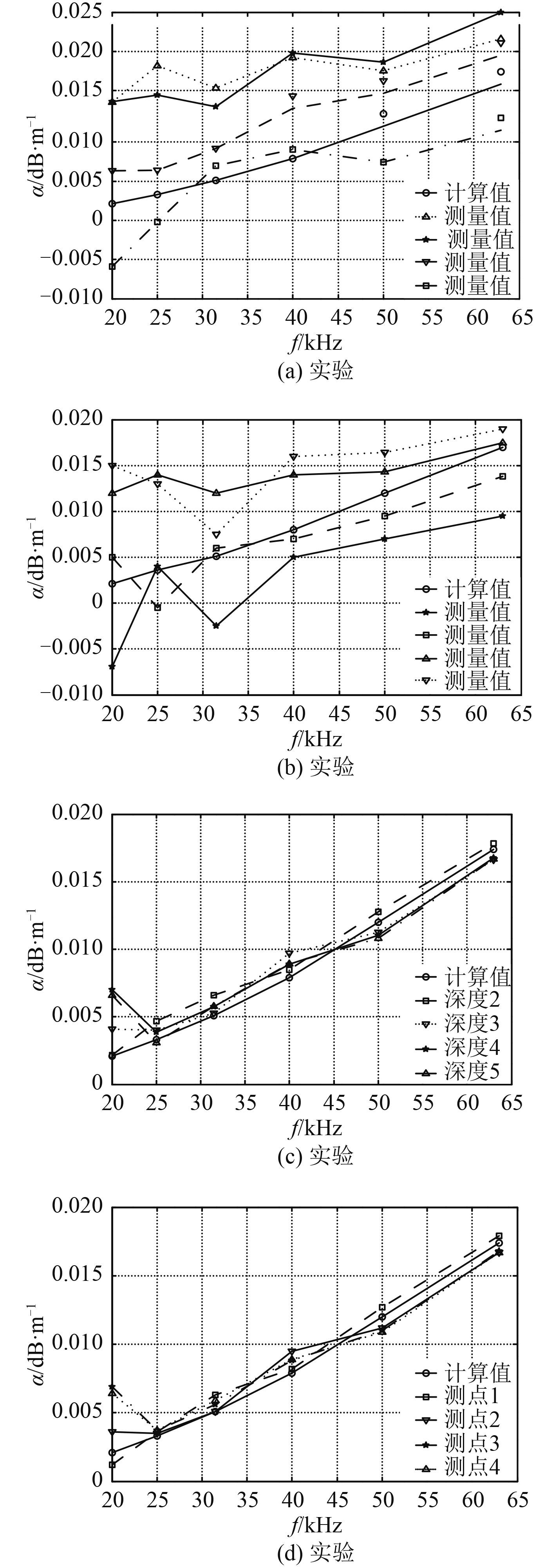
上述4组实验测量得到的实验结果如图 7所示。
|
图 7 声吸收系数的测量值与理论计算值的比较 Fig. 7 The comparison of sound absorption coefficient between the measured value and the calculated value by the theory |
实验1和实验2中进行了多次试验测量,为方便图示,图 7(a)和图 7(b)中仅示出了其中4次试验测量结果与文献[13]中理论公式计算值的比较。由这2组实验得到的MgSO4溶液的声吸收系数(水听器电缆引起的声吸收已进行修正)比理论计算值大几倍乃至几十倍,个别频率点甚至出现负值,这也是文献[4]中的测量结果为负值的原因,因为聚乙烯塑料袋在搅拌过程中会发生变形,从而使得声压级衰减曲线发生变化,而由固定点的水听器得到的混响时间计算的声吸收系数将会存在巨大的误差。因此,这2种混响时间测量方法引起的声吸收系数误差非常大,是不可取的。
图 7(c)为测点位置的深度相同、同一水平面内混响时间值平均之后得到的MgSO4溶液的声吸收系数与理论计算值的比较。每个深度测点为18个,图中仅示出4个深度的测量结果。该组测量得到的声吸收系数与理论计算值的平均误差约为13%。因此,在利用共振器测量液体介质声吸收系数时,把混响时间数据进行空间平均能在一定程度上减少测量误差。
图 7(d)中为利用在纯水和MgSO4溶液中位置相同的4个测点的混响时间测量得到的声吸收系数与理论计算值的比较,平均误差约为11%。
在20 kHz时,测量值与理论公式计算值之间的偏差较大。这是因为由阻尼常数可求得共振器内简正波共振峰的平均宽度约为2.7 Hz,由式(11)和式(12)可得到2.7 Hz带宽内简正波的数目为0.58,刚好满足混响场条件的下限频率[15]。共振器内声场扩散不均匀性的下限频率也可按文献[16]中的施罗德截止频率公式求得,经计算为22 kHz。这表明共振器内简正模态数目少,使得声场扩散不充分,引起了较大的测量误差。因此,在22 kHz以下频段不应在该共振器中采用混响法测量液体介质的声吸收系数。
该实验系统的误差来源有:溶液体积测量的误差、温度测量的误差、传感器电缆长度测量的误差、电子设备电噪声引起的误差等,故图 7(d)中的测量误差是上述所有误差之和[15]。因为低频段、低浓度混浊海水的声吸收系数是约为10-3量级的小量,要测量这样量级的声信号非常困难。但是从图 7(d)中可见,实验测量的声吸收变化曲线与理论公式计算的声吸收变化曲线一致;除20 kHz频率外,其余频率的误差都小于11%。这样的误差对于研究混浊海水的声吸收规律来说,影响可以忽略。而同类型的共振器[4, 17]的测量误差为15%,因此本文设计的共振器及测量系统是成功的。
在图 7(c)和图 7(d)中,实验3和实验4中测量的声吸收系数平均值几乎重合。这是因为当对式(3)进行微分后,MgSO4溶液的逾量声吸收:
| $ \Delta \alpha \propto - (\Delta T/{T^2})\text{。} $ | (24) |
当不同空间位置处的混响时间相差很小时,可将T约掉,声吸收系数的变化:
| $ \Delta \alpha \propto - \Delta T\text{。} $ | (25) |
因此,声吸收系数的变化仅取决于混响时间的差别,所以由混响时间平均所得到的声吸收系数与4个测点混响时间所得到的平均声吸收系数差别不大。但是如果共振器中同一深度、不同空间位置处的声压级衰减曲线差别较大,声场扩散性变差时,则由混响时间平均所得到的声吸收系数将大大偏离理论计算值。
实验3和实验4中MgSO4溶液声吸收系数的测量误差如表 1所示。实验4的测量误差比实验3要小。实验3的测点总数为90个,记录的混响时间数据为900个。而实验4为空间位置严格固定的测点,测点数为4个,记录的混响时间数据仅为40个。可见实验4的测量工作量比实验3小得多,且测量误差更小。因此,这为低浓度混浊海水声吸收系数的实验测量提供了一种误差较小的方法。
|
|
表 1 实验3和实验4 MgSO4溶液声吸收系数的测量误差 Tab.1 Relative measurement error of sound absorption coefficient of magnesium sulfate solution in 3, 4 % |
综合前文所述,这里给出采用共振器测量液体介质声吸收时的指导原则如下:
1)发射换能器和水听器与共振器边界之间距离大于λ/2(λ为研究频段中的最大波长);
2)共振器在实验过程中,必须保证形状不能发生变化;
3)在采用纯水标定共振器的声损耗和在待测溶液的混响时间测量过程中,混响时间的测点位置必须精确可重复,当测点数达到4个时,可使混响法测量的声吸收系数的误差控制在5%以内。
5 结语本文通过对一圆柱形共振器内的声场进行理论分析,发现在共振器内不同的空间位置得到的声压级衰减曲线不同,因而不同空间位置处的混响时间也不同。在此基础上,构建并研制了一套声吸收测量系统,以MgSO4溶液的声吸收系数理论计算值作为标准,校验了不同混响时间测量方法所引起的声吸收系数测量误差,给出了误差(5%以内)较小的液体介质声吸收系数实验测量指导原则。
本文的研究成果为浅海混浊水域的海水声吸收系数实验测量、总结含悬浮泥沙颗粒海水介质的声吸收规律、海水声学混浊与光学混浊特性分析等方面的研究提供了一定的参考。
| [1] | RICHARDS S D. The effect of temperature, pressure, and salinity on sound attenuation in turbid seawater[J]. The Journal of the Acoustical Society of America , 1998, 103 (1) :205–211. DOI: 10.1121/1.421088 |
| [2] | 彭临慧, 王桂波. 悬浮颗粒物海水及其声吸收[J]. 声学技术 , 2008, 27 (2):168–171. |
| [3] | 彭临慧, 王桂波. 中国近海悬浮颗粒物海水声波衰减[J]. 声学学报 , 2008, 33 (5):389–395. |
| [4] | BROWN N R, LEIGHTON T G, RICHARDS S D, et al. Measurement of viscous sound absorption at 50-150 kHz in a model turbid environment[J]. The Journal of the Acoustical Society of America , 1998, 104 (4) :2114–2120. DOI: 10.1121/1.423725 |
| [5] | RICHARDS S D, LEIGHTON T G, BROWN N R. Sound absorption by suspensions of nonspherical particles:Measurements compared with predictions using various particle sizing techniques[J]. The Journal of the Acoustical Society of America , 2003, 114 (4) :1841–1850. DOI: 10.1121/1.1610449 |
| [6] | 刘永伟, 李琪, 商德江, 等. 混浊海水声吸收与温度、盐度、压强关系[J]. 声学技术 , 2012, 31 (2):156–161. |
| [7] | 文洪涛, 杨燕明, 刘贞文, 等. 近海混浊水的附加声衰减研究--实验测量值与考虑粒径分布的理论估算值的比较[J]. 声学学报 , 2010, 35 (1):45–52. |
| [8] | 裘辛方, 韩嗣康. 海水中硫酸镁弛豫声吸收的温度关系[J]. 声学学报 , 1987, 12 (2):151–154. |
| [9] | 裘辛方.海水声吸收问题[M]//中国科学院声学研究所.国外水声学进展.北京:科学出版社, 1966:150-153. |
| [10] | 杜功焕, 朱哲民, 龚秀芬. 声学基础[M].第2版. 南京: 南京大学出版社, 2001: 417-449. |
| [11] | 何祚镛, 赵玉芳. 声学理论基础[M]. 北京: 国防工业出版社, 1981: 113-134. |
| [12] | MORSE P M, INGARD K U. Theoretical acoustics[M]. New York: McGraw-Hill Book Company, 1968: 576-598. |
| [13] | SCHULKIN M, MARSH H W.海水声吸收[M]//声学译丛-水声学(水声物理专辑)[M].上海:上海市科学技术编译馆, 1965:57-60. |
| [14] | 王荣津. 水声材料手册[M]. 北京: 科学出版社, 1983: 103-115. |
| [15] | 李琪.水筒噪声测量方法研究[D].哈尔滨:哈尔滨船舶工程学院, 1990:44-55. |
| [16] | SCHROEDER M R. Measurement of sound diffusion in reverberation chambers[J]. The Journal of the Acoustical Society of America , 1959, 31 (11) :1407–1414. DOI: 10.1121/1.1907643 |
| [17] | EDMONDS P D, LAMB J. A method for deriving the acoustic absorption coefficient of gases from measurement of the decay-time of a resonator[J]. Proceedings of the Physical Society , 1958, 71 (1) :17–32. DOI: 10.1088/0370-1328/71/1/303 |
 2016, Vol. 38
2016, Vol. 38
