2. 哈尔滨工程大学水声工程学院, 黑龙江 哈尔滨 150001
2. College of Underwater Acoustic Engineering University, Harbin 150001, China
分布式MIMO技术最近受到广泛的关注,分布式MIMO天线系统的概念最早在1987年提出[1]。近些年开始应用于声呐目标定位中,相比于传统的阵列声呐,MIMO声呐具有更高的自由度和更好的信息截获性能[2-4]。文献[5]提出了一种在二维平面内搜索目标的分布式MIMO算法,上述算法充分地利用了MIMO声呐空间分集和压缩感知算法的性能优势[6],相比于传统成像BP算法而言能够在使用较少的实验数据基础上显著地提高其成像性能[7]。然而上述算法只是在二维平面内搜索,没有涉及到三维空间目标搜索和空间左右模糊问题。
声矢量传感器目前主要应用于水声警戒声呐、鱼雷探测声呐、水下导航定位等领域。在空气声学中,它可以用于探测隐形飞机、声强和声功率测量、噪声源识别等。20世纪50年代美国学者使用惯性传感器来直接测量水下质点振速[8],到20世纪70 -80年代苏联学者用其研制的声矢量传感器研究海洋环境噪声[9],直到20世纪90年代声矢量传感器才开始成为水声界研究热点之一。声矢量传感器可以同时获得声场中的声压、质点振速的3个正交分量的信息[10]。从而获得声场中的更多的信息,更加有利于水下目标的定位估计,性能上优于声压传感器,目前声矢量传感器已经被广泛地应用于DOA估计中。矢量阵常规波束形成算法,如矢量阵M V D R波束形成算法,具有高分辨力,但该算法在有噪声干扰或失配问题的情况下,性能会受到严重影响,使其在实际应用中遇到困难[11]。
在2006年,Candes,Donoho,Tao等提出了压缩感知理论。在该理论下,如果在某变换域内信号是可压缩的或者是稀疏的,就可以用远低于奈奎斯特(Nyquist)理论所需的采样率来进行采样,然后再通过某种信号重构算法从有限的采样数据中精准的恢复原信号[12]。在实际的目标定位和声源方位估计中,相比于整个测量空间,空间中的目标个数往往是稀疏的,这正满足了信号的稀疏特性,因此在压缩感知理论下,作为用于目标或声源的方位估计方法有如下好处:采样率可以不满足信号中心频率的两倍,可以用少量的实验数据精准的重构信号;不需要预先的估计信号源数目;相干的信号源也可以用压缩感知方法直接进行处理;在阵元数比声源数小的情形下也可以进行正常的方位估计等[13]。因此被很快的应用到DOA估计和声呐成像中。
本文提出了一种声矢量传感器分布式MIMO声呐空间成像算法,利用声矢量信息解决了左右模糊问题;该算法基于DCD算法改进的OMP算法[14-15],在采用小快拍数据的基础上,避免了重构信号中的矩阵求逆时所带来的数值不稳定,提高了运算速率,性能更优于BP算法;且在小信噪比小于-5 dB条件下,抗噪声能力优于声压OMP-DCD算法,定位精度更高。
1 系统模型 1.1 声压阵的稀疏表示设在空间x-y平面上,有M个发射器和N个接收器,三维空间上有L个目标,共接收到MN组数据。对于声压MIMO接收信号为
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{n}}, $ | (1) |
| $ \mathit{\boldsymbol{S}} = \mathit{\boldsymbol{h}}\left( n \right) \times s\left( n \right) + u\left( n \right)。 $ | (2) |
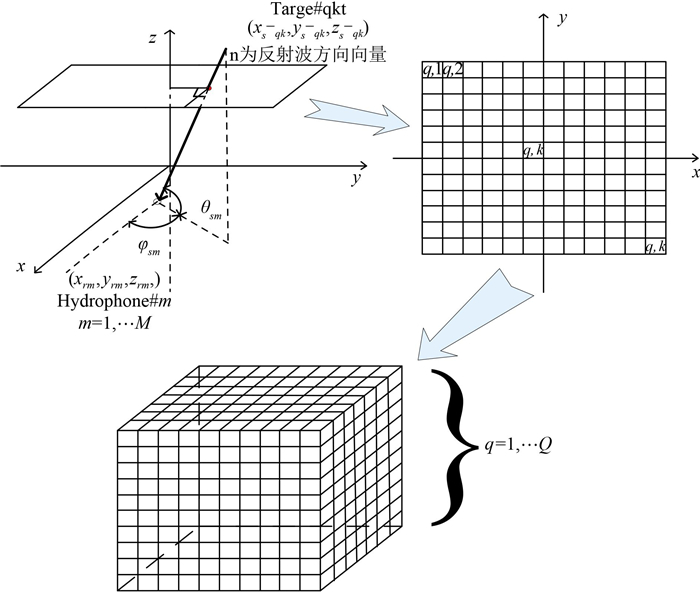
式中:y为接收信号;S为回波信号;h为脉冲冲击响应;*表示卷积;s为发射信号;n为均值为0,方差为σ2的加性噪声。如图 1所示,将目标所在空间划分为Q个平面,每个平面划分为K个网格。q,k表示的是第q个空间平面的第k个网格。脉冲冲击响应为发射信号经过目标反射回来的时延,因整个空间只存在L个真实目标,因此在h上只有L个非零元素。
|
图 1 系统定位模型 Fig. 1 The localization model |
根据各个发射和接收传感器与目标空间上各个区域的相对位置关系,可以得到第m个发射传感器到第q,k个空间区域再到第n个接收传感器的距离qnm-qk[16]
| $ \begin{split} \\[-12pt] {r_{nm - qk}} = \sqrt {{{\left( {{x_{rn}} \!-\!{x_{qk}}} \right)}^2}\!+\!{{\left( {{y_{rn}}\!-\!{y_{qk}}} \right)}^2}\!+\!{{\left( {{z_{rn}}\!-\!{z_{qk}}} \right)}^2}} +\!\\ \sqrt {{{\left( {{x_{tm}} - {x_{qk}}} \right)}^2} + {{\left( {{y_{tm}} - {y_{qk}}} \right)}^2} + {{\left( {{z_{tm}} - {z_{qk}}} \right)}^2}} {\text{。}} \end{split} $ | (3) |
| $ \begin{array}{l} {r_{nm - qc}} = \sqrt {{{\left( {{x_{rn}}\!-\!{x_{qc}}} \right)}^2}\!+\!{{\left( {{y_{rn}}\!-\!{y_{qc}}} \right)}^2}\!+\!{{\left( {{z_{rn}}\!-\!{z_{qc}}} \right)}^2}} + \\ \sqrt {{{\left( {{x_{tm}} - {x_{qc}}} \right)}^2} + {{\left( {{y_{tm}} - {y_{qc}}} \right)}^2} + {{\left( {{z_{tm}} - {z_{qc}}} \right)}^2}}{\text{。}} \end{array} $ | (4) |
| $ {R_{nm - qk}} = {r_{nm - qk}} - {r_{nm - qk}}{\text{。}} $ | (5) |
式中:(xtm
,ytm
,ztm
)分别为第m个发射传感器的坐标;(xrn
,yrn
,zrn
)分别为第n个接收传感器的z坐标;(xqk
,yqk
,zqk
)为第q,k个网格的位置坐标;(xqc
,yqc
,zqc
)为第q个平面的参考点处的位置坐标;则Rnm-qk
为第q个平面内的第k个网格到该平面参考点处的距离。则相应的平面内压缩感知矩阵为
| $ \begin{array}{l} \!F\!\left( {{{{A}}_{qk}}} \right) \!\!=\!\! \left[{{{\rm e}^{-{\rm j}\frac{w}{c}{R_{k1}}}}, \!{{\rm e}^{-{\rm j}\frac{w}{c}{R_{k2}}}}, \! \cdots \!, {{\rm e}^{-{\rm j}\frac{w}{c}{R_{kmn}}}}\!, \! \cdots \!, {{\rm e}^{ - {\rm j}\frac{w}{c}{R_{kMN}}}}} \right] \! \cdot \! \!\!F\left( {{{{S}}_0}} \right)\text{,}\\ k = 1, \cdots K{\text{。}} \end{array} $ | (6) |
其中,S0为目标在成像参考点出的回波信号,F为傅里叶变换。由此知道信号重构的是脉冲冲击响应的相应信息。
1.2 声矢量阵的稀疏表示由于声矢量接收传感器可以接收到声压信息和质点振速的3个正交分量,进一步扩展可以得到4维矢量接收信号的稀疏表达式[16]
| $ {\mathit{\boldsymbol{y}}_v} = {\mathit{\boldsymbol{A}}_v}\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{n}}_v}。 $ | (7) |
可知,A v为4D ×K ×Q维的空间压缩感知矢量矩阵,yv为4D × 1 ×Q维的接收信号。D为快拍数和所用数据组个数的乘积。可将A v表示为[16]
| $ {\mathit{\boldsymbol{A}}^{\left( v \right)}} = \left[{\begin{array}{*{20}{c}} \mathit{\boldsymbol{A}}\\ {{\mathit{\boldsymbol{A}}^{\left( x \right)}}}\\ {{\mathit{\boldsymbol{A}}^{\left( y \right)}}}\\ {{\mathit{\boldsymbol{A}}^{\left( z \right)}}} \end{array}} \right]。 $ | (8) |
其中,A (x),A (y),A (z)分别是x向,y向,z向的振速聚焦压缩感知矩阵[16],它们和A 有如下关系
| $ {\mathit{\boldsymbol{A}}^{\left( x \right)}} = {\mathit{\boldsymbol{a}}^{\left( x \right)}} \odot \mathit{\boldsymbol{A}}, $ | (9) |
| $ {\mathit{\boldsymbol{A}}^{\left( y \right)}} = {\mathit{\boldsymbol{a}}^{\left( y \right)}} \odot \mathit{\boldsymbol{A}}, $ | (10) |
| $ {\mathit{\boldsymbol{A}}^{\left( z \right)}} = {\mathit{\boldsymbol{a}}^{\left( z \right)}} \odot \mathit{\boldsymbol{A}}。 $ | (11) |
其中,⊙为Hadamard积,表示相对应的元素相乘。
| $ {\mathit{\boldsymbol{a}}^{\left( x \right)}} = \left\{ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{a}}_{11}^{\left( x \right)}}&{\mathit{\boldsymbol{a}}_{12}^{\left( x \right)}}& \cdots &{\mathit{\boldsymbol{a}}_{1k}^{\left( x \right)}}& \cdots &{\mathit{\boldsymbol{a}}_{1K}^{\left( x \right)}}\\ {\mathit{\boldsymbol{a}}_{21}^{\left( x \right)}}&{\mathit{\boldsymbol{a}}_{22}^{\left( x \right)}}& \cdots &{\mathit{\boldsymbol{a}}_{2k}^{\left( x \right)}}& \cdots &{\mathit{\boldsymbol{a}}_{2K}^{\left( x \right)}}\\ \vdots&\vdots&\ddots&\vdots&\ddots&\vdots \\ {\mathit{\boldsymbol{a}}_{Q1}^{\left( x \right)}}&{\mathit{\boldsymbol{a}}_{Q2}^{\left( x \right)}}& \cdots &{\mathit{\boldsymbol{a}}_{Qk}^{\left( x \right)}}& \cdots &{\mathit{\boldsymbol{a}}_{QK}^{\left( x \right)}} \end{array}} \right\}, $ | (12) |
| $ {\mathit{\boldsymbol{a}}^{\left( y \right)}} = \left\{ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{a}}_{11}^{\left( y \right)}}&{\mathit{\boldsymbol{a}}_{12}^{\left( y \right)}}& \cdots &{\mathit{\boldsymbol{a}}_{1k}^{\left( y \right)}}& \cdots &{\mathit{\boldsymbol{a}}_{1K}^{\left( y \right)}}\\ {\mathit{\boldsymbol{a}}_{21}^{\left( y \right)}}&{\mathit{\boldsymbol{a}}_{22}^{\left( y \right)}}& \cdots &{\mathit{\boldsymbol{a}}_{2k}^{\left( y \right)}}& \cdots &{\mathit{\boldsymbol{a}}_{2K}^{\left( y \right)}}\\ \vdots&\vdots&\ddots&\vdots&\ddots&\vdots \\ {\mathit{\boldsymbol{a}}_{Q1}^{\left( y \right)}}&{\mathit{\boldsymbol{a}}_{Q2}^{\left( y \right)}}& \cdots &{\mathit{\boldsymbol{a}}_{Qk}^{\left( y \right)}}& \cdots &{\mathit{\boldsymbol{a}}_{QK}^{\left( y \right)}} \end{array}} \right\}, $ | (13) |
| $ {\mathit{\boldsymbol{a}}^{\left( z \right)}} = \left\{ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{a}}_{11}^{\left( z \right)}}&{\mathit{\boldsymbol{a}}_{12}^{\left( z \right)}}& \cdots &{\mathit{\boldsymbol{a}}_{1k}^{\left( z \right)}}& \cdots &{\mathit{\boldsymbol{a}}_{1K}^{\left( z \right)}}\\ {\mathit{\boldsymbol{a}}_{21}^{\left( z \right)}}&{\mathit{\boldsymbol{a}}_{22}^{\left( z \right)}}& \cdots &{\mathit{\boldsymbol{a}}_{2k}^{\left( z \right)}}& \cdots &{\mathit{\boldsymbol{a}}_{2K}^{\left( z \right)}}\\ \vdots&\vdots&\ddots&\vdots&\ddots&\vdots \\ {\mathit{\boldsymbol{a}}_{Q1}^{\left( z \right)}}&{\mathit{\boldsymbol{a}}_{Q2}^{\left( z \right)}}& \cdots &{\mathit{\boldsymbol{a}}_{Qk}^{\left( z \right)}}& \cdots &{\mathit{\boldsymbol{a}}_{QK}^{\left( z \right)}} \end{array}} \right\}, $ | (14) |
分别是x,y,z向的聚集的单位矢量矩阵[16],表达式如下:
| $ \begin{split} {\bf{a}}_{qk}^{\left( x \right)} \!\!=\!\! & \left[{\cos {\theta _{qk1}}\cos {\varphi _{qk1}}, \cdots, \cos {\theta _{qkm}}\cos\! {\varphi _{qkm}}, \!\!\cdots, } \right.\\ & {\left. {\cos {\theta _{qkM}}\cos {\varphi _{qkM}}} \right]^{\rm{T}}{\text{,}}} \end{split} $ | (15) |
| $ \begin{aligned} {\bf{a}}_{qk}^{\left( y \right)} = & \left[{\sin {\theta _{qk1}}\sin {\varphi _{qk1}}, \cdots, \sin {\theta _{qkm}}\sin {\varphi _{qkm}}, \cdots, } \right.\\ & {\left. {\sin {\theta _{qkM}}\sin {\varphi _{qkM}}} \right]^{\rm{T}}{\text{,}}} \end{aligned} $ | (16) |
| $ {\bf{a}}_{qk}^{\left( z \right)} = {\left[{\sin {\theta _{qk1}}, \cdots, \sin {\theta _{qkm}}, \cdots, \sin {\theta _{qkM}}} \right]^{\rm{T}}{\text{。}}} $ | (17) |
θqkm 为第q,k个空间区域对应于第m个接收传感器的俯仰角,范围θqkm ∈[-π/2,π/2]。φqkm ∈[0,2π]为第qk空间区域对应第m个接收传感器的方位角,有[16]
| $ {\theta _{qkm}} ={\rm{t}}{{\rm{a}}{\rm{n}}^{ - 1}}\left( {\frac{{{z_{qk}} - {z_m}}}{{\sqrt {{{\left( {{x_{qk}} - {x_m}} \right)}^2} + {{\left( {{y_{qk}} - {y_m}} \right)}^2}} }}} \right) {\text{,}}$ | (18) |
| $ {\varphi _{qkm}} = {\rm{t}}{{\rm{a}}{\rm{n}}^{ - 1}}\left( {\frac{{{y_{qk}} - {y_m}}}{{\sqrt {{{\left( {{x_{qk}} - {x_m}} \right)}^2} + {{\left( {{y_{qk}} - {y_m}} \right)}^2}} }}} \right) {\text{。}}$ | (19) |
tan-1表示反正切函数。
2 声矢量OMP-DCD算法式(7)此类求解属于NP-hard非优化问题。针对此类优化问题,采用改进的正交匹配追踪算法来求解声矢量传感器条件下的重构信号,具体思想是:以贪婪迭代的方法来选择压缩感知矢量矩阵Av的列,使在每次迭代中,选择与当前的残差最大程度相关的列,从测量向量中减去与其相关部分并反复的迭代,直到达到终止条件,迭代停止。
声矢量OMP算法的具体实现步骤如下:
输入压缩感知矢量矩阵A v,矢量接收信号y v,目标个数L;
输出x
的L-稀疏的逼近
初始化
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{r}}_0} = {\mathit{\boldsymbol{y}}_v}, \\ {\mathit{\boldsymbol{I}}_0} = \left[{} \right]。\\ l = 0, \end{array} \right. $ | (20) |
其中,I 0为支撑集;r 0为信号残余;l为迭代次数。
循环执行步骤1-步骤4。
步骤1:从A v矩阵中抽取列向量与信号残余进行比较并找出最相关的原子。arg max表示的是找寻最匹配原子位置。
| $ {i_l} = \arg \;\max \left| {\left\langle {{\mathit{\boldsymbol{r}}_{l-1}}, {\mathit{\boldsymbol{a}}_{v, i}}} \right\rangle } \right|, $ | (21) |
步骤2:更新支撑集,找到与信号残余最相关的原子,将其导入支撑集中。
| $ {\mathit{\boldsymbol{I}}_l} = {\mathit{\boldsymbol{I}}_{l-1}} \cup \left\{ {{i_l}} \right\}, $ | (22) |
步骤3:更新残余。剔除支撑集中已经包含的信息。
| $ {\mathit{\boldsymbol{r}}_l} = \mathit{\boldsymbol{y}}-{\mathit{\boldsymbol{A}}_{v, {{\rm{I}}_l}}}\mathit{\boldsymbol{A}}_{v, {{\rm{I}}_l}}^ + \cdot {\mathit{\boldsymbol{y}}_v}, $ | (23) |
步骤4:判断终止条件,若满足,则迭代停止;若不满足,则执行步骤1。
根据压缩信号和支撑集对信号进行重构。如式(24)所示。
| $ {{\mathit{\boldsymbol{\hat x}}}_l} = \mathit{\boldsymbol{A}}_{v, {{\rm{I}}_l}}^ + \cdot {\mathit{\boldsymbol{y}}_v}。 $ | (24) |
在OMP算法中,需要进行矩阵求逆,但在现实中求矩阵的逆很难实现,所以采用加入DCD算法来解决矩阵求逆问题,从而降低运算复杂度。表 1描述了声矢量OMP-DCD算法具体流程[17]。
|
|
表 1 声矢量OMP-DCD算法 Tab.1 Acoustic vector OMP-DCD algorithm |
在二维平面内有4个发射器,16个接收器,3个散射点,它们的位置坐标如表 2。经过研究,压缩感知算法使用较少的数据也可以得到较为精确的结果,所以在进行压缩感知数据处理时,只采用64组数据中的20组,而且只采用每组数据中150个采样点,这样大大减少了运算量。这样总的实验数据为20 × 150个采样点。在声矢量接收传感器中,就会接收到声压和振速的信息,即4 × 20 × 150个采样点数据。
|
|
表 2 位置坐标 Tab.2 Sensors and targets location |
假 设所有反射点在空间上是理想的,产生一个发射信号,信噪比为10 dB。成像区域为一个2.1 m × 2.1 m × 180 m的三维空间。发射信号波形为PN码,PN码是由{-1,1}组成的集合,序列长度为216-1,字符频率为96 kps,通带频率为2.5~30 kHz,由此可知距离分辨率为
| $ {d_{res}} \geqslant \frac{c}{{2 \cdot BW}} \geqslant \frac{{1000\;{\rm{m}}/{\rm{s}}}}{{2 \cdot 27.5\;{\rm{kHz}}}} \geqslant 18.18\;{\rm{mm}}{\text{。}} $ | (25) |
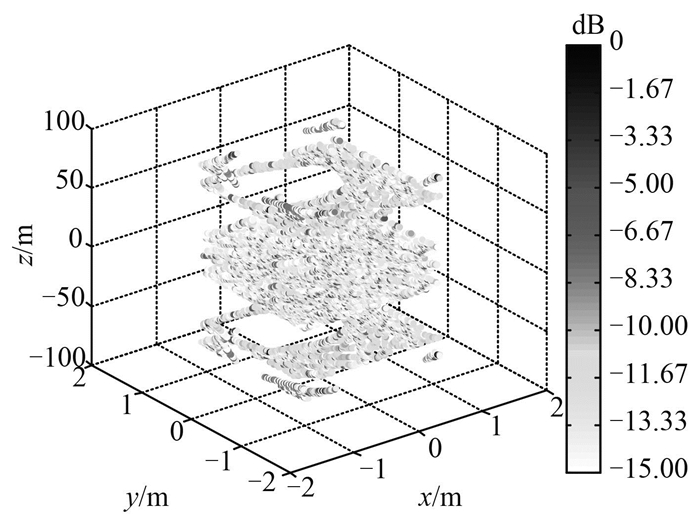
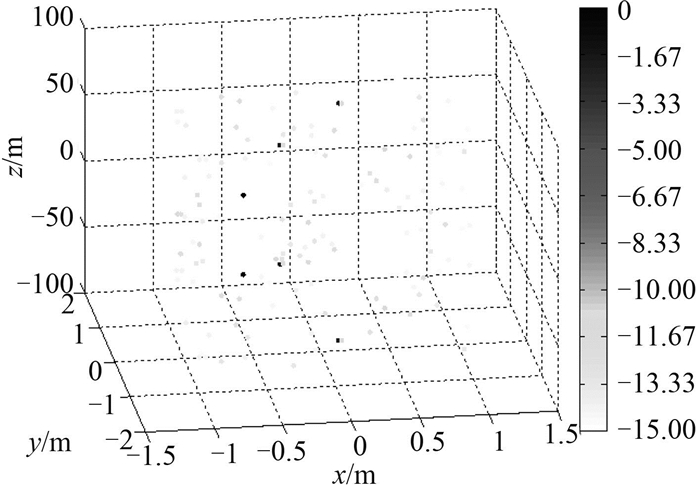
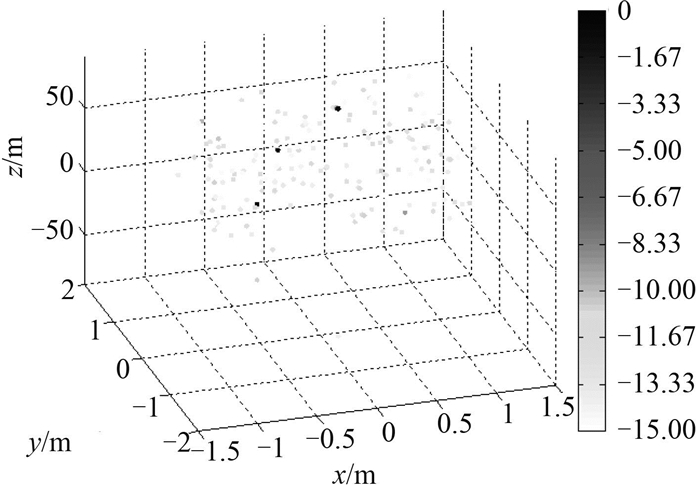
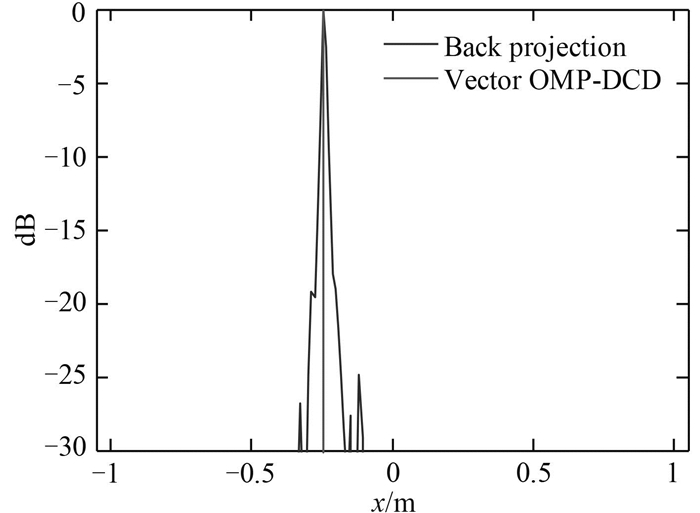
由图 2~图 4的对比可以看出,OMP-DCD算法在采用比BP算法更少的数据基础上仍可以获得稀疏解,定位精度更高;由图 5~图 7可知,SNR为10 dB时,BP算法有较宽的主瓣、旁瓣,在目标三的空间平面内,当主瓣级为0 dB时,x轴方向最大旁瓣级-24.5 dB,y轴方向最大旁瓣级为-24.3 dB,z轴方向最大旁瓣级为-5.5 dB;采用声矢量OMP-DCD算法可以精准的在空间确定目标的方位,而且与声压OMP-DCD算法相比,可以有效地解决目标的左右模糊问题。
|
图 2 反向投影算法空间目标成像 Fig. 2 Imaging results of back projection algorithm |
|
图 3 声压OMP-DCD算法空间目标成像 Fig. 3 Imaging results of scalar OMP-DCD algorithm |
|
图 4 声矢量OMP-DCD算法空间目标成像 Fig. 4 Imaging results of acoustic vector OMP-DCD algorithm |
|
图 5 在Target#3所在y-z平面空间谱随x的变化 Fig. 5 Spatial spectrum with x in they-z plane of the target#3 |
|
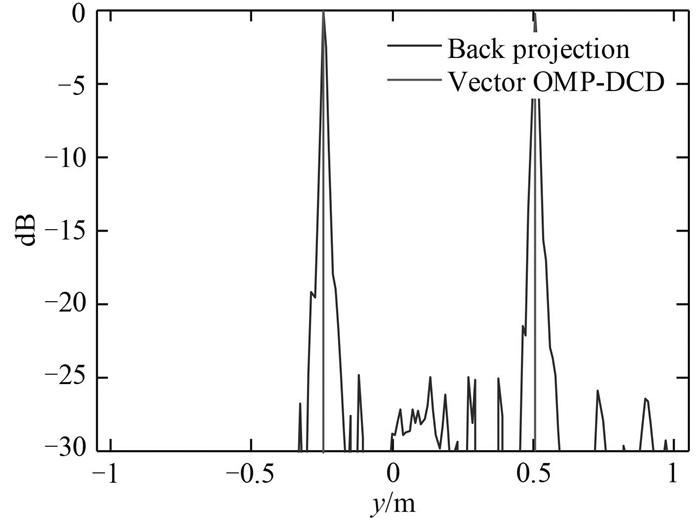
图 6 在Target#3所在x-z平面空间谱随y的变化 Fig. 6 Spatial spectrum with y in thex-z plane of the target#3 |
|
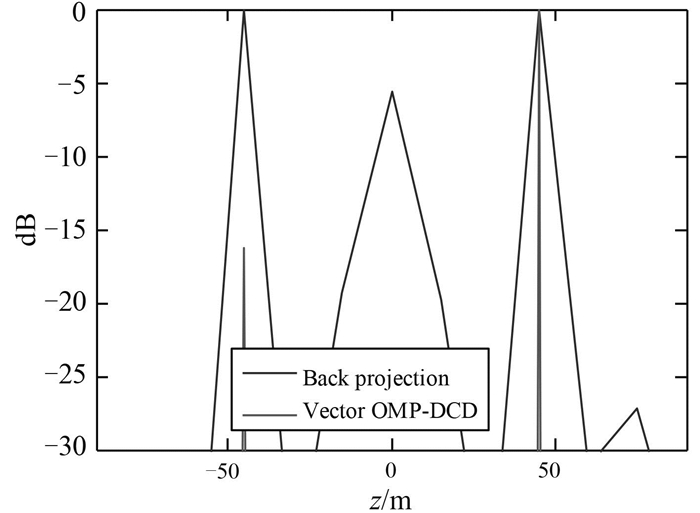
图 7 在Target#3所在x-y平面空间谱随z的变化 Fig. 7 Spatial spectrum with z in thex-y plane of the target#3 |
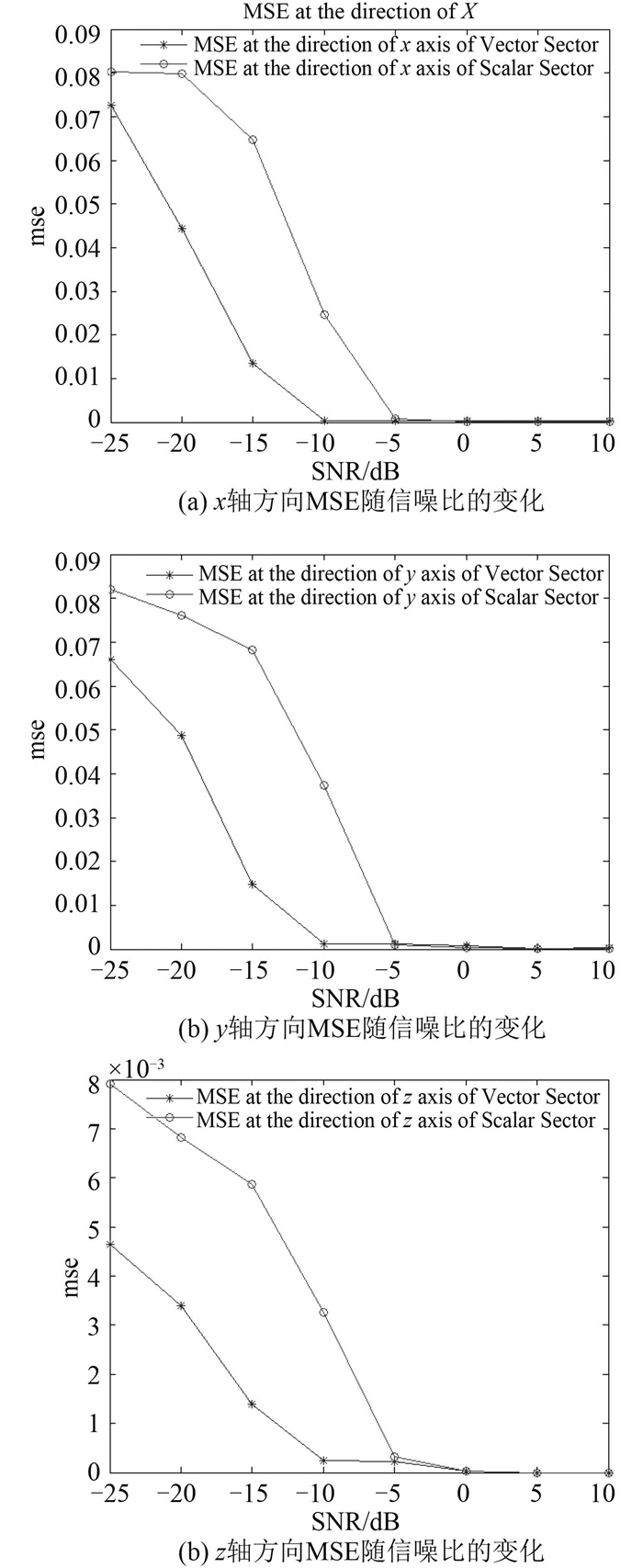
由图 8仿真结果表明,在信噪比小于-5 dB条件下,声矢量OMP-DCD算法比声压OMP-DCD算法在各个方向上的定位误差要小,具有较高的抗噪声能力和较高的定位精度。
|
图 8 声压与声矢量传感器条件下x,y,z轴方向MSE随信噪比的变化 Fig. 8 The MSE of scalar and vector sensor OMP-DCD of x, y, z axis with different SNR |
本文提出了一种基于声矢量传感器的分布式MIMO声呐成像方法,该方法采用了改进的基于压缩感知的声矢量OMP-DCD算法。研究表明该算法采用比BP算法更少的试验数据,且BP算法有较宽的主瓣和旁瓣信息,当主瓣级为0 dB,x轴方向、y轴方向和z轴方向最大旁瓣级分别为-24.5 dB,-24.3 dB和-5.5 dB,而提出的算法可以直接获得稀疏解,实现空间目标的精准定位。而且避免了正常求解过程中矩阵求逆时的数值不稳定,降低了运算复杂度;在信噪小于-5 dB条件下,定位精度高于声压OMP-DCD算法,具有较强的抗噪声能力;基于声矢量传感器的声速信息,使左右模糊问题得到了有效的解决,进一步地提高了分布式MIMO声呐的系统辨识能力。
| [1] | SALEH A A M, RUSTAKO A, ROMAN R. Distributed antennas for indoor radio communication[J]. IEEE Transactions on Communications , 1987, 35 (12) :1245–1251. DOI: 10.1109/TCOM.1987.1096716 |
| [2] | WANG H Y, LIAO G S, WANG Y, et al. On parameter identifiability of MIMO radar with waveform diversity[J]. Signal Processing , 2011, 91 (8) :2057–2063. DOI: 10.1016/j.sigpro.2011.03.012 |
| [3] | GOGINENI S, NEHORAI A. Sparsity-based MIMO noise radar for multiple target estimation[C]//Proceedings of the 7th Sensor Array and Multichannel Signal Processing Workshop. Hoboken, NJ, USA:IEEE, 2012:33-36. |
| [4] | HASSANIEN A, VOROBYOV S A. Subspace-based direction finding using transmit energy focusing in MIMO radar with colocated antennas[C]//Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing. Prague, Czech Republic:IEEE, 2011:2788-2791. |
| [5] | WILLIAMS T. SONAR imaging using compressive sensing[J]. Ohio State:The Ohio State University , 2011 . |
| [6] | DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory , 2006, 52 (4) :1289–1306. DOI: 10.1109/TIT.2006.871582 |
| [7] | MCCORKLE J W. Focusing of synthetic aperture ultra wideband data[C]//Proceedings of IEEE International Conference on Systems Engineering. USA:IEEE, 1991:1-5. |
| [8] | LESLIE C B, KENDALL J M, JONES J L. Hydrophone for measuring particle velocity[J]. The Journal of the Acoustical Society of America , 1956, 28 (4) :711–715. DOI: 10.1121/1.1908455 |
| [9] | ZAKHAROV L N. Phase-gradient measurements in sound fields[J]. Soc. Phys. Acoust , 1974, 20 (3) :241–245. |
| [10] |
杨德森, 洪连进.
矢量水听器原理及应用引论[M]. 北京: 科学出版社, 2009.
YANG De-sen, HONG Lian-jin. Principle and application of the introduction of vector hydrophone[M]. Beijing: Science Press, 2009. |
| [11] | CHO Y T, ROAN M J. Adaptive near-field beamforming techniques for sound source imaging[J]. The Journal of the Acoustical Society of America , 2009, 125 (2) :944–957. DOI: 10.1121/1.3050248 |
| [12] | CANDES E J, WAKIN M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine , 2008, 25 (2) :21–30. DOI: 10.1109/MSP.2007.914731 |
| [13] | BARANIUK R G. Compressive sensing[Lecture Notes][J]. IEEE Signal Processing Magazine , 2007, 24 (4) :118–121. DOI: 10.1109/MSP.2007.4286571 |
| [14] | ZAKHAROV Y V, TOZER T C. Multiplication-free iterative algorithm for LS problem[J]. Electronics Letters , 2004, 40 (9) :567–569. DOI: 10.1049/el:20040353 |
| [15] | CAI T T, WANG L. Orthogonal matching pursuit for sparse signal recovery with noise[J]. IEEE Transactions on Information Theory , 2011, 57 (7) :4680–4688. DOI: 10.1109/TIT.2011.2146090 |
| [16] |
时洁, 杨德森, 时胜国, 等. 基于压缩感知的矢量阵聚焦定位方法[J]. 物理学报 , 2016, 65 (2):024302.
SHI Jie, YANG De-sen, SHI Sheng-guo, et al. Compressive focused beamforming based on vector sensor array[J]. Acta Physica Sinica , 2016, 65 (2) :024302. |
| [17] | ZAKHAROV Y V, NASCIMENTO V. Orthogonal matching pursuit with DCD iterations[J]. Electronics Letters , 2013, 49 (4) :295–297. DOI: 10.1049/el.2012.3923 |
 2016, Vol. 38
2016, Vol. 38
