2. 哈尔滨工程大学水声工程学院, 黑龙江 哈尔滨 150001
2. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
在信道均衡技术中常用的算法有递推最小二乘算法(RLS) [1],这种算法是一种具有稳健的误差表现和快速收敛性质的常规算法,所以RLS算法不仅在接收机自适应均衡滤波器得到了广泛的应用,在系统辨识等方面也得到很多关注[2]。但是当输入信号被噪声干扰时,RLS算法估计的结果不是无偏估计而是有偏估计,此时RLS算法的自适应滤波效果会退化,所以在考虑输入信号和输出信号都含有噪声的情况,采用总体最小二乘(TLS)算法对系统进行估计能够得到无偏估计结果[3]。在信道为稀疏信道时,为了充分利用信道的稀疏性,相应的稀疏正则化的RLS算法和TLS算法被提出[4-6]。随着MIMO技术的发展,为了消除信号多径传播引起的符号间干扰,相应的自适应均衡技术也得到了广泛的关注和研究[7]。在MIMO系统信道均衡技术中,贝尔实验室垂直分层空时结构(V-BLAST)效果显著,V-BLAST最初设计是解决平衰落MIMO信道中由于多径传播产生的符号间干扰,进而提高均衡判决的可靠性和准确性[8]。应用RLS算法的MIMO系统的线性均衡和判决反馈均衡和各种降低均衡计算复杂度V-BLAST的改善算法[9-10],都没有针对MIMO线性均衡系统输入和输出含有噪声的情况进行研究。
本文在MIMO系统模型线性均衡的基础上,针对稀疏MIMO系统提出了一种适用于均衡输入信号和输出信号都含有噪声干扰的RTLS算法。TLS算法避免了RLS算法在输入信号含有噪声时估计有偏的问题;算法通过加入变遗忘因子提高算法适应不同信道环境的能力;通过加入ℓ1范数和ℓ0范数实现充分利用信道稀疏性的目的,进而提高均衡算法的MSE和BER表现。
1 MIMO系统模型考虑一个具有M根发射天线和N根接收天线的稀疏MIMO信道系统,可以得到在时刻n发射信号与接收信号的关系[11]:
| $ \mathit{\boldsymbol{x}}\left( n \right) = \sum\limits_{l = 0}^L \mathit{\boldsymbol{H}} \left( l \right)s\left( {n-l} \right) + {\mathit{\boldsymbol{n}}_i}\left( n \right)。 $ | (1) |
其中,用一个N × M的矩阵H(l)代表MIMO系统中所有子信道的第l个信道冲击响应采样参数,由于信道是稀疏信道,所以矩阵H(l)中绝大多数元素为0。在第i个发射天线和第j个接收天线之间的脉冲响应向量中的元素由hji(l)表示,其中i=1,…M;j=1,…N。若Lc是MIMO子信道长度则l=1,…Lc,那么MIMO信道采样冲击响应矩阵如下[11]:
| $ \mathit{\boldsymbol{H}}\left( l \right) = \left[{\begin{array}{*{20}{c}} {{h_{11}}\left( l \right)}& \cdots &{{h_{1M}}\left( l \right)}\\ \vdots&\ddots&\vdots \\ {{h_{N1}}\left( l \right)}& \cdots &{{h_{NM}}\left( l \right)} \end{array}} \right], l = 0, \cdots, {L_c}{\rm{。}} $ |
发射信号
图 1是MIMO系统的线性均衡器的输入和输出都含有噪声干扰的示意图。由图 1看出,在线性均衡滤波过程中的训练阶段,含均值为0,方差为σo2的高斯白噪声干扰no(n)的训练序列即为线性滤波器的设计输出信号ℓ0;在判决阶段,y(n)的硬判决结果视为线性滤波器的设计输出信号d(n)。
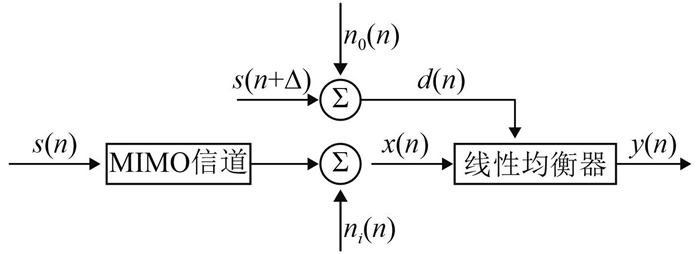
|
图 1 MIMO线性均衡模型 Fig. 1 MIMO linear equalization model |
MIMO系统的线性均衡示意图和均衡滤波器结构图分别如图 2(a)和图 2(b)所示,其中卍表示对均衡器输出信号的硬判决。

|
图 2 线性均衡器示意图 Fig. 2 Linear equalization diagram |
由图 2(b)可以看出MIMO系统的线性均衡器包含M个子均衡滤波器且定义每个子均衡滤波器的参数向量为:
| $ {\mathit{\boldsymbol{w}}_i}\left( n \right) = {\left[{\begin{array}{*{20}{c}} {\mathit{\boldsymbol{w}}_{i, 1}^{\rm{T}}\left( n \right)}&{\mathit{\boldsymbol{w}}_{i, 2}^{\rm{T}}\left( n \right)}& \cdots &{\mathit{\boldsymbol{w}}_{i, N}^{\rm{T}}\left( n \right)} \end{array}} \right]^{\rm{T}}} $ |
其中i=1,…,M,并且wi(n)为NL × 1的向量包含了N个L × 1的滤波器向量,即
| $ {\mathit{\boldsymbol{w}}_{i, j}}\left( n \right) = {\left[{{w_1}\left( n \right){w_3}\left( n \right) \cdots {w_L}\left( n \right)} \right]^{\rm{T}}}{\rm{。}} $ |
其中j=1,…,N,L为每个滤波器向量的长度。则在n时刻MIMO系统线性均衡滤波器系数矩阵为:
| $ \mathit{\boldsymbol{W}}\left( n \right) = \left[{\begin{array}{*{20}{c}} {{{\bf{w}}_1}\left( n \right)}&{{{\bf{w}}_2}\left( n \right)}& \cdots &{{\mathit{\boldsymbol{w}}_M}\left( n \right), } \end{array}} \right] $ |
W(n)为LN × M的矩阵。从图 2(a)中可以看出线性均衡器的输入信号均为MIMO接收天线接收的混有高斯白噪声ni(n)的接收信号。在时刻n,每个滤波器wi,j(n)的输入信号可以用一个L × 1的向量表示:
| $ {\mathit{\boldsymbol{x}}_i}\left( k \right) = {\left[{\begin{array}{*{20}{c}} {{x_i}\left( n \right)}&{{x_i}\left( {n-1} \right)}& \cdots &{{x_i}\left( {n-L + 1} \right)} \end{array}} \right]^{\rm{T}}}{\rm{ 。}} $ |
其中i=1,…,N。那么每个子均衡滤波器的输入信号为:
| $ \mathit{\boldsymbol{x}}\left( n \right) = {\left[{\begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}_1^{\rm{T}}\left( n \right)}&{\mathit{\boldsymbol{x}}_2^{\rm{T}}\left( n \right)}& \cdots &{\mathit{\boldsymbol{x}}_N^{\rm{T}}\left( n \right)} \end{array}} \right]^{\rm{T}}}{\rm{, }} $ |
则MIMO系统线性均衡滤波器的输出信号为:
| $ \mathit{\boldsymbol{y}}\left( n \right) = {\mathit{\boldsymbol{W}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{x}}\left( n \right){\rm{。}} $ | (2) |
为了使对线性均衡滤波器系数矩阵W(n)估计的代价函数J(W(n))达到最小值,可以使对每个均衡子滤波器系数向量wi(n)估计的代价函数J(wi(n))最小[3, 12]:
| $ \mathit{\boldsymbol{W}}\left( n \right) = \mathop {\min }\limits_{\mathit{\boldsymbol{W}}\left( n \right)} J\left( {\mathit{\boldsymbol{W}}\left( n \right)} \right) = \mathop {\min }\limits_{{w_i}\left( n \right)} \sum\limits_{i = 1}^M {J\left( {{\mathit{\boldsymbol{w}}_i}\left( n \right)} \right)} {\rm{。}} $ | (3) |
式(3)中
| $ J\left( {{\mathit{\boldsymbol{w}}_i}\left( n \right)} \right) = \frac{{\mathit{\boldsymbol{w}}_i^{\rm{T}}\left( n \right)\mathit{\boldsymbol{R}}\left( n \right)-2\mathit{\boldsymbol{w}}_i^{\rm{T}}\left( n \right)\mathit{\boldsymbol{p}}\left( n \right) + \delta \left( n \right)}}{{\mathit{\boldsymbol{w}}_i^{\rm{T}}\left( n \right){\mathit{\boldsymbol{w}}_i}\left( n \right) + \beta }}。 $ | (4) |
其中R(n)为含噪声输入信号x(n)的时间平均自相关矩阵:
| $ \mathit{\boldsymbol{R}}\left( n \right) = \lambda \left( n \right)\mathit{\boldsymbol{R}}\left( {n-1} \right) + \mathit{\boldsymbol{x}}\left( n \right){{\bf{x}}^{\rm{T}}}\left( n \right){\rm{。}} $ | (5) |
p(n)是设计输出信号d(n)与含噪声输入信号x(n)的时间平均互相关矩阵:
| $ \mathit{\boldsymbol{p}}\left( n \right) = \lambda \left( n \right)\mathit{\boldsymbol{p}}\left( {n-1} \right) + {d_i}\left( n \right){\bf{x}}\left( n \right){\rm{。}} $ | (6) |
δ(n)是设计输出信号d(n)的时间平均能量:
| $ \delta (n) = \lambda (n)\delta (n - 1) + d_i^2(n) \text{。} $ | (7) |
且
为了充分利用MIMO信道系统稀疏性,在代价函数中加入可以体现均衡滤波器先验稀疏性质的惩罚函数Js(wi(n))。Js(wi(n))可以是wi(n)估计值的ℓ1范数或ℓ0范数,由于ℓ0范数为非凸的,所以取用近似ℓ0范数。ℓ1范数和近似ℓ0范数惩罚函数分别如下[4]:
| $ {\left\| {{\mathit{\boldsymbol{w}}_i}\left( n \right)} \right\|_1} = \sum\limits_{l = 0}^{NL-1} {\left| {{w_{i, l}}\left( n \right)} \right|} {\rm{, }} $ | (8) |
| $ {\left\| {{\mathit{\boldsymbol{w}}_i}\left( n \right)} \right\|_0} \approx NL-\sum\limits_{l = 0}^{NL-1} {\exp \left\{ {-\alpha \left| {{w_{i, l}}\left( n \right)} \right|} \right\}} {\rm{。}} $ | (9) |
其中α是一个大于0的常数,则代价函数重新定义为:
| $ {J_r}\left( {{\mathit{\boldsymbol{w}}_i}\left( n \right)} \right) = J\left( {{\mathit{\boldsymbol{w}}_i}\left( n \right)} \right) + \gamma {J_s}\left( {{\mathit{\boldsymbol{w}}_i}\left( n \right)} \right){\rm{, }} $ | (10) |
其中γ≥0为正则化参数,其作用是控制Js(wi(n))对代价函数的影响。
为了获得适应信道n时刻变化情况的遗忘因子λ(n)且能够使Js(wi(n))最小,采用最速下降法获得λ(n)的更新等式:
| $ \lambda \left( {n + 1} \right) = \lambda \left( n \right) + \mu \frac{{\partial {J_r}\left( {{\mathit{\boldsymbol{w}}_i}\left( n \right)} \right)}}{{\partial \lambda \left( n \right)}}{\rm{。}} $ | (11) |
其中μ为一个微调参数,根据式(5)~式(7)得到:
| $ \begin{array}{l} \frac{{\partial {J_r}\left( {{\mathit{\boldsymbol{w}}_i}\left( n \right)} \right)}}{{\partial \lambda \left( n \right)}} = \frac{1}{{\mathit{\boldsymbol{w}}_i^{\rm{T}}\left( n \right){\mathit{\boldsymbol{w}}_i}\left( n \right) + \beta }} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {\mathit{\boldsymbol{w}}_i^{\rm{T}}\left( n \right)\mathit{\boldsymbol{R}}\left( {n-1} \right){\mathit{\boldsymbol{w}}_i}\left( n \right)} \right.-\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;2\mathit{\boldsymbol{w}}_i^{\rm{T}}\left( n \right)\mathit{\boldsymbol{p}}\left( {n-1} \right) + \delta \left. {\left( {n - 1} \right)} \right)。 \end{array} $ | (12) |
则λ(n)的更新等式如下且λ(n)∈[λmin λmax]:
| $ \begin{array}{l} \lambda \left( {n + 1} \right) = \lambda \left( n \right) + \frac{\mu }{{\mathit{\boldsymbol{w}}_i^{\rm{T}}\left( n \right){\mathit{\boldsymbol{w}}_i}\left( n \right) + \beta }} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {\mathit{\boldsymbol{w}}_i^{\rm{T}}\left( n \right)\mathit{\boldsymbol{R}}\left( {n-1} \right){\mathit{\boldsymbol{w}}_i}\left( n \right)} \right.-\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;2\mathit{\boldsymbol{w}}_i^{\rm{T}}\left( n \right)\mathit{\boldsymbol{p}}\left( {n-1} \right) + \delta \left. {\left( {n - 1} \right)} \right)。 \end{array} $ | (13) |
由于ℓ1范数和近似ℓ0范数惩罚函数的不可微分性,所以采用次梯度分析代价函数Jr(wi(n)),对wi(n)估计使代价函数最小,此处用符号▽s表示对函数关于wi(n)的次梯度。则Jr(wi(n))对wi(n)的次梯度为:
| $ \begin{array}{l} \nabla J\left( {{\mathit{\boldsymbol{w}}_i}\left( n \right)} \right) = \frac{2}{{\mathit{\boldsymbol{w}}_i^{\rm{T}}\left( n \right){\mathit{\boldsymbol{w}}_i}\left( n \right) + \beta }} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {\mathit{\boldsymbol{w}}_i^{\rm{T}}\left( n \right)\mathit{\boldsymbol{R}}} \right.\left( n \right){\mathit{\boldsymbol{w}}_i}\left( n \right)-\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{p}}\left( n \right)-J\left( {{\mathit{\boldsymbol{w}}_i}\left( n \right)} \right)\left( {{\mathit{\boldsymbol{w}}_i}\left( n \right)} \right)。 \end{array} $ | (14) |
其中当Js(wi(n))取ℓ1范数和近似ℓ0范数惩罚函数时次梯度分别为[6]:
| $ {\nabla ^s}{\left\| {{\mathit{\boldsymbol{w}}_i}\left( n \right)} \right\|_1} = {\rm{sgn}}\left\{ {{\mathit{\boldsymbol{w}}_i}\left( n \right)} \right\}{\rm{, }} $ | (16) |
| $ \begin{array}{*{20}{l}} {{\nabla ^s}{{\left\| {{\mathit{\boldsymbol{w}}_i}\left( n \right)} \right\|}_0} \approx \alpha {\rm{diag}}\left\{ {{\rm{sgn}}\left( {{\mathit{\boldsymbol{w}}_i}\left( n \right)} \right)} \right\} \times }\\ {{\rm{exp}}\left\{ {-\alpha \left| {{\mathit{\boldsymbol{w}}_i}\left( n \right)} \right|} \right\}{\rm{。}}} \end{array} $ | (17) |
在wi(n-1)处计算代价函数Js(wi(n))下降方向向量表示为:
| $ \mathit{\boldsymbol{d}}\left( {n-1} \right) = {\left. {-\left\{ {{\nabla ^s}{J_r}\left( {{\mathit{\boldsymbol{w}}_i}\left( n \right)} \right)} \right\}} \right|_{\tau \left( {n-1} \right) = 0}}{\rm{。}} $ | (18) |
其中τ(n-1)是计算更新wi(n)时的步长,即
| $ {\mathit{\boldsymbol{w}}_i}\left( n \right) = {\mathit{\boldsymbol{w}}_i}\left( {n-1} \right) + \tau \left( {n-1} \right)\mathit{\boldsymbol{d}}\left( {n-1} \right){\rm{。}} $ | (19) |
设置辅助步长
| $ \mathit{\boldsymbol{\tilde d}}\left( {n-1} \right) = {\left. {\left\{ {\mathit{\boldsymbol{d}}\left( {n-1} \right)} \right\}} \right|_{\gamma = 0}}{\rm{。}} $ | (20) |
对代价函数
| $ a\left( n \right){\tilde \tau ^2}\left( {n - 1} \right) + b\left( n \right)\tilde \tau \left( {n - 1} \right) + c\left( n \right) = 0\text{。} $ | (21) |
其中:
| $ \begin{array}{l} la\left( n \right) = \mathit{\boldsymbol{w}}_i^{\rm{T}}\left( {n-1} \right)\mathit{\boldsymbol{\tilde d}}\left( {n-1} \right){{\mathit{\boldsymbol{\tilde d}}}^{\rm{T}}}\left( {n-1} \right) - \\ \;\left\| {\mathit{\boldsymbol{\tilde d}}\left( {n - 1} \right)} \right\|_2^2\left( {\mathit{\boldsymbol{w}}_i^{\rm{T}}\left( {n - 1} \right)\mathit{\boldsymbol{q}}\left( n \right) - {{\mathit{\boldsymbol{\tilde d}}}^{\rm{T}}}\left( {n - 1} \right)\mathit{\boldsymbol{p}}\left( n \right)} \right), \end{array} $ | (22) |
| $ b\left( n \right) = \xi \left( n \right){{\mathit{\boldsymbol{\tilde d}}}^{\rm{T}}}\left( {n-1} \right)\mathit{\boldsymbol{q}}\left( n \right)-\eta \left( n \right)\left\| {\mathit{\boldsymbol{\tilde d}}\left( {n-1} \right)} \right\|_2^2{\rm{, }} $ | (23) |
| $ \begin{array}{l} lc\left( n \right) = \xi \left( n \right)\left( {\mathit{\boldsymbol{w}}_i^{\rm{T}}\left( {n-1} \right)\mathit{\boldsymbol{q}}\left( n \right)-{{\mathit{\boldsymbol{\tilde d}}}^{\rm{T}}}\left( {n-1} \right)\mathit{\boldsymbol{p}}\left( n \right)} \right) - \\ \eta \left( n \right)\mathit{\boldsymbol{w}}_i^{\rm{T}}\left( {n - 1} \right){{\mathit{\boldsymbol{\tilde d}}}^{\rm{T}}}\left( {n - 1} \right)。 \end{array} $ | (24) |
等式中
| $ \mathit{\boldsymbol{q}}\left( n \right) = R\left( n \right)\mathit{\boldsymbol{\tilde d}}\left( {n-1} \right){\rm{, }} $ | (25) |
| $ \xi \left( n \right) = \left\| {{\mathit{\boldsymbol{w}}_i}\left( {n-1} \right)} \right\|_2^2 + \beta {\rm{, }} $ | (26) |
| $ \begin{array}{*{20}{l}} {\eta \left( n \right) = \mathit{\boldsymbol{w}}_i^{\rm{T}}\left( {n-1} \right){\bf{R}}\left( n \right){\mathit{\boldsymbol{w}}_i}\left( {n-1} \right)}\\ {-2{\bf{w}}_i^{\rm{T}}\left( {n - 1} \right)\mathit{\boldsymbol{p}}\left( n \right) + \delta \left( n \right){\rm{。}}} \end{array} $ | (27) |
根据一元二次方程求解公式
仿真对比分析了RLS算法、RTLS算法、ℓ1-RTLS算法、ℓ0-RTLS算法、VFF-ℓ1-RTLS算法、VFF-ℓ0-RTLS算法对稀疏MIMO信道系统线性均衡滤波的均方误差(MSE)曲线。
MIMO信号传输系统采用M=2发射天线,N=2接收天线,每条MIMO信道子路径脉冲响应向量长度Lc=30,因为是稀疏信道,假设每条子路径脉冲响应向量中有K=2个元素为非零值,其他元素皆为0;线性均衡滤波器的输入信号所含噪声的方差σi2=0.1,设计输出信号所含噪声的方差σo2=0.1;每个均衡滤波器长度一般要大于或等于信道多途扩展长度,通过线性搜索仿真过程中每个线性均衡滤波器长度L=60;RLS算法中输入信号自相关矩阵初始值R(-1)=0.1I,RTLS算法、ℓ1-RTLS算法、ℓ0-RTLS算法、VFF-ℓ1-RTLS算法、VFF-ℓ0-RTLS算法中输入信号自相关矩阵初始值R(-1)=0;固定遗忘因子λ=0.996,变遗忘因子范围

|
图 3 K=2,SNR=10 dB时各算法MSE曲线 Fig. 3 MSE curves of algorithms when K=2, SNR=10 dB |
从图 3中可以看出,在MIMO系统线性均衡器输入信号和设计输出信号都含有噪声干扰时,RTLS算法的MSE收敛速度比RLS算法的收敛速度慢,但是RLS算法由于噪声的影响,最终收敛效果没有RTLS算法好。与RTLS算法相比较,ℓ1-RTLS算法、ℓ0-RTLS算法由于其利用了MIMO信道稀疏性质,MSE不仅收敛速度快,而且稳定收敛值低。在这些算法中,VFF-ℓ0-RTLS算法、VFF-ℓ0-RTLS算法不仅能够保持算法的收敛速度,并且可以达到更低的稳定收敛值。
改变MIMO信道系统的稀疏程度,比较各算法的MSE稳定收敛值,结果如图 4所示。从图 4中可以看出,随着稀疏程度越来越小,各算法的性能都有所下降,但在稀疏程度不同的情况下,RTLS算法始终比RLS算法的MSE效果低0.5~1 dB;VFF-ℓ0-RTLS算法在信道稀疏程度比较低的情况下比RLS算法的MSE效果低约1.5 dB,在信道稀疏程度不高的情况下效果接近RTLS算法;VFF-ℓ1-RTLS算法的效果始终保持最低的MSE值,比RLS算法的MSE收敛效果提高约2 dB。
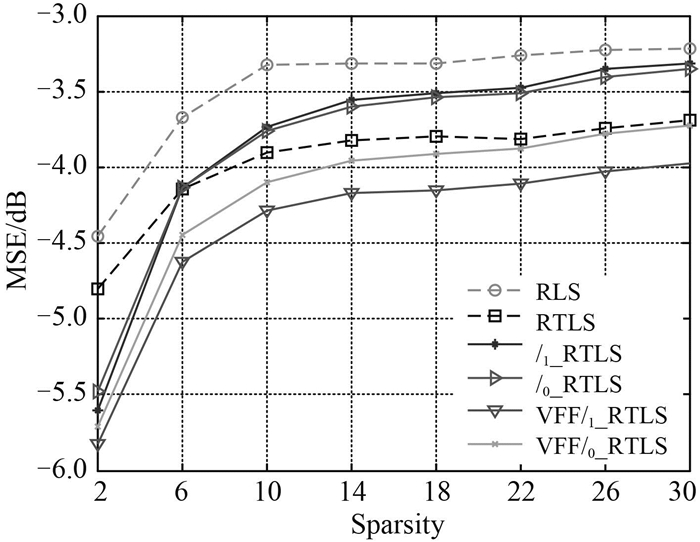
|
图 4 SNR=10 dB时不同稀疏程度各算法收敛MSE Fig. 4 Convergence MSE of algorithms when sparsity is different when SNR=10 dB |
图 5是在信噪比为10 dB时MIMO信道输入输出天线个数不同情况下的VFF-ℓ0-RTLS算法与VFF-ℓ1-RTLS算法线性均衡的收敛MSE值随信道稀疏程度变化的曲线。从图 5中可以看出发射天线和接收天线数量相同的情况下,随着收发天线个数的增加均衡效果变差;在发射天线数量一定的情况下,随着接收天线数量的增大均衡效果越好。
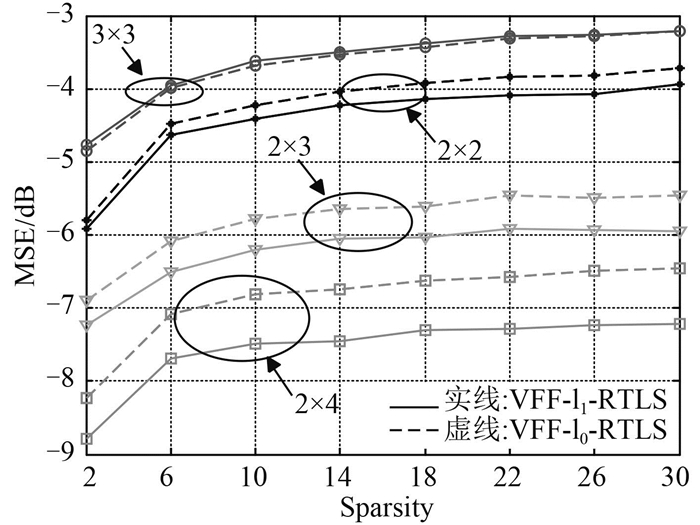
|
图 5 SNR=10 dB时2 × 2,3 × 3,2 × 3,2 × 4 MIMO稀疏信道情况的VFF-ℓ0-RTLS算法与VFF-ℓ1-RTLS算法的收敛MSE Fig. 5 SNR=10 dB时2 × 2, 3 × 3, 2 × 3, 2 × 4 Convergence MSE of VFF-ℓ0-RTLS algorithm and VFF-ℓ1-RTLS algorithm and 2 × 2, 3 × 3, 2 × 3, 2 × 4 MIMO systems when SNR=10 dB |
图 6显示了在2 × 2的MIMO稀疏系统中(K=2)发送3 000个BPSK信号,其中含1 000个训练序列时各算法线性均衡的BER表现。保持线性均衡器的输入噪声方差σi2和输出噪声方差σo2相等,随着信噪比的与RLS算法的BER表现越接近,信噪比大于11 dB时RTLS算法的BER与RLS算法的BER相同,但VFF-ℓ0-RTLS算法与VFF-ℓ0-RTLS算法的BER表现依然优于RLS算法和RTLS算法。
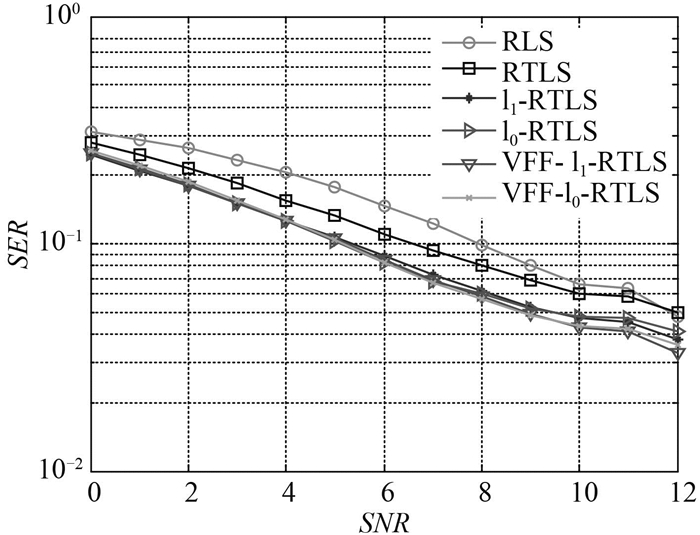
|
图 6 2 × 2 MIMO系统中不同信噪比情况下线性均衡BER Fig. 6 BER of linear equalization in 2 × 2 MIMO system at different SNR |
图 7为在2 × 4的MIMO稀疏系统中各算法线性均衡的BER表现。与2 × 2的仿真条件相同的情况下,可以看出各算法的BER表现都有所提高;由于算法趋于稳定时,输入信号向量的自相关矩阵可用其期望值代替,所以最小二乘估计偏差只与输入端噪声有关[3],随着信噪比的增大,输入噪声方差σi2减小,RLS算法估计偏差逐渐减小;由于输入噪声方差σi2和输出噪声方差σo2的比值β不变,根据式(4)可以发现β对TLS算法的代价函数的影响不变,但是随着噪声的减小,β的影响会使TLS算法表现趋于稳定,而不再有所提高。从图 7中看出RTLS估计在信噪比为9 dB时,RLS算法的BER表现已经比ℓ0-RTLS算法的BER表现好;随着信噪比的进一步增大到11 dB,RLS算法的BER表现最好。
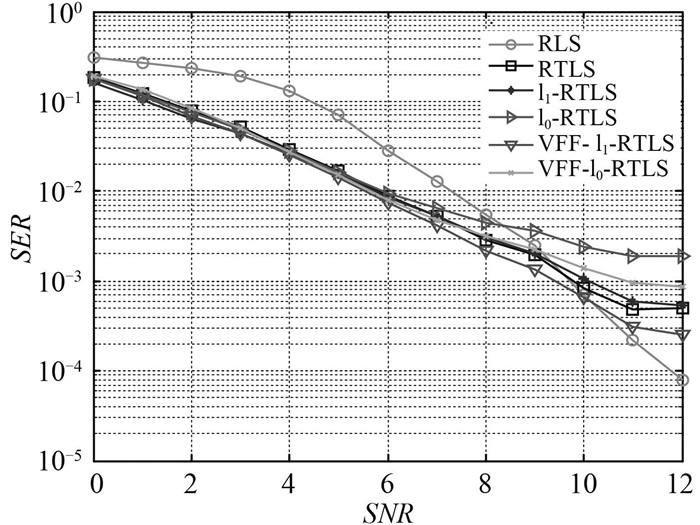
|
图 7 2 × 4 MIMO 系统中不同信噪比情况下线性均衡 BER Fig. 7 BER of linear equalization in 2 × 4 MIMO system at different SNR |
在稀疏MIMO系统线性均衡过程中,利用最速下降法更新遗忘因子λ,并利用次梯度下降法更新均衡滤波器系数,使加入惩罚函数ℓ1范数或ℓ0范数的RTLS代价函数,即加入ℓ1范数或ℓ0范数的瑞利商最小。惩罚函数充分利用了MIMO系统的稀疏性;变遗忘因子提高了算法对信道变化的适应能力。仿真对比变遗忘因子算法和固定遗忘因子算法均衡结果的MSE曲线说明,在一定信噪比范围内VFF-ℓ1-RTLS算法和VFF-ℓ0-RTLS算法对均衡器输入信号和输出信号都含有噪声情况的稀疏系统模型有更优的MSE表现;该算法的均衡效果随着稀疏程度的减小而衰退并且与MIMO系统发射天线和接收天线的个数有关。
| [1] | HAYKIN S. Adaptive filter theory[M]. Upper Saddle River, HJ: Prentice Hall, 2002. |
| [2] | LJUNG L, SÖDERSTRÖM T. Theory and practice of recursive identification[M]. Cambridge, MA: MIT Press, 1983. |
| [3] | DAVILA C E. An efficient recursive total least squares algorithm for FIR adaptive filtering[J]. IEEE Transactions on Signal Processing , 1994, 42 (2) :268–280. DOI: 10.1109/78.275601 |
| [4] | EKSIOGLU E M, TANC A K. RLS algorithm with convex regularization[J]. IEEE Signal Processing Letters , 2011, 18 (8) :470–473. DOI: 10.1109/LSP.2011.2159373 |
| [5] | ZAKHAROV Y V, NASCIMENTO V H. DCD-RLS adaptive filters with penalties for sparse identification[J]. IEEE Transactions on Signal Processing , 2013, 61 (12) :3198–3213. DOI: 10.1109/TSP.2013.2258340 |
| [6] | TANC A K. Sparsity regularized recursive total least-squares[J]. Digital Signal Processing , 2015, 40 :176–180. DOI: 10.1016/j.dsp.2015.02.018 |
| [7] | MALEKI-TEHRANI A, HASSIBI B, CIOFFI J M. Adaptive equalization of multiple-input multiple-output (MIMO) frequency selective channels[C]//Proceedings of the 33rd Asilomar Conference on Signals, Systems, and Computers. Pacific Grove, CA:IEEE, 1996:547-551. |
| [8] | FOSCHINI G J, GOLDEN G D, VALENZUELA R A, et al. Simplified processing for high spectral efficiency wireless communication employing multi-element arrays[J]. IEEE Journal on Selected Areas in Communications , 1999, 17 (11) :1841–1852. DOI: 10.1109/49.806815 |
| [9] | MALEKI-TEHRANI A, HASSIBI B, CIOFFI J M. Adaptive equalization of multiple-input multiple-output (MIMO) channels[C]//Proceedings of 2000 IEEE International Conference on Communications. New Orleans, LA:IEEE, 2000:1607-1674. |
| [10] | ARABLOUEI R, DOĞANÇAY K. Low-complexity adaptive decision-feedback equalization of MIMO channels[J]. Signal Processing , 2011, 92 (6) :1515–1524. |
| [11] | RONTOGIANNIS A A, KEKATOS V, BERBERIDIS K. An adaptive decision feedback equalizer for time-varying frequency selective MIMO channels[C]//Proceedings of the 7th Workshop on Signal Processing Advances on Wireless Communications. Cannes, France:IEEE, 2006. |
| [12] | FENG D Z, ZHANG X D, CHANG D X, et al. A fast recursive total least squares algorithm for adaptive FIR filtering[J]. IEEE Transactions on Signal Processing , 2004, 52 (10) :2729–2737. DOI: 10.1109/TSP.2004.834260 |
 2016, Vol. 38
2016, Vol. 38
