0 引言

水下目标探测的主要设备仍然是声呐系统，声呐是海军舰船的重要武器装备之一，承担对潜艇、舰艇及其他水中目标进行探测、定位和识别等重要任务^[1]。在实际的海洋探测情况中，真实目标的使用代价很大，由于受海洋环境、使用条件和成本等因素的限制，采用目标模拟器对真实目标进行模拟，更加实用。在多基地声呐协同探测中，如果缺乏真实目标的回波数据将无法准确的实现对多基地声呐中对目标的探测、定位与跟踪。声呐波形设计是声呐检测系统的重要组成部分，从理论与技术角度讲，不存在理想的最佳波形能使所有指标都能达到最佳，并适用于各种应用环境，因此在进行声呐波形设计的时候要根据本身的条件、主要性能指标要求以及使用环境合理设计声呐波形^[2-3]。本文根据实际需要多基地声呐目标模拟器的波形设计方法并对目标模拟器的应用背景及整体框架进行介绍。

本文所设计的目标模拟器应用于多基地协同探测试验中，其定位几何模型如图 1所示。T为发射站，R为接收站，它与发射站分开配置，只能被动接受来自目标的回波，因此具有很好的隐蔽性。S为目标。我们用目标模拟器代替真实的目标，实现接收并延迟转发主动声呐信号的功能。

r_T和r_R分别为发射站和接收站与目标之间的距离。而一般情况下，接收站测量的则是发射站到目标与接收站到目标的距离和，即r_∑=r_T+r_R。

D为接收站到发射站的距离，即基线长度。

θ_T和θ_R分别为发射站和接收站测量的角度，β=θ_R-θ_T为目标与发射站和接收站之间的夹角。

为了便于讨论，作以下假设。1）接收站和发射站位置固定不变；2）信号沿直线传的；3）不考虑多途效应；4）各基站测量误差服从各自独立的零均值高斯白分布。

研究基于接收站测量信息（r_∑，θ_R）的定位方法。基于接收站测量信息的定位方程可表示为：

$ \left\{ \begin{array}{l} {r_{_\Sigma} } = {r_{_T}} + {r_{_R}} = \sqrt {{{(x - {x_{_T}})}^2} + {{(y - {y_{_T}})}^2}} + \\[8pt] \quad \quad\sqrt {{{(x - {x_{_R}})}^2} + {{(y - {y_{_R}})}^2}} \text{，}\\[8pt] {\theta _R} = \arctan \displaystyle\frac{{y - {y_{_R}}}}{{x - {x_{_R}}}}\text{。} \end{array} \right. $

(1)

由上式可以解得目标S的位置坐标为：

$ \left\{ \begin{array}{l} x = {x_{_R}} + {r_{_R}}\cos {\theta _{_R}} \text{，}\\ y = {y_{_R}} + {r_{_R}}\sin {\theta _{_R}}\text{。} \end{array} \right. $

(2)

其中， ${r_{_R}} \!=\! \displaystyle\frac{{r_\Sigma ^2 - [{{({x_{_R}} \!-\! {x_{_T}})}^2} \!+\! {{({y_{_{_R}}} \!-\! {y_{_T}})}^2}]}}{{2[{r_{_\Sigma }} \!+\! ({x_{_R}} \!-\! {x_{_T}})\cos {\theta _{_R}} \!+\! ({y_{_R}} \!-\! {y_{_T}})\sin {\theta _{_R}}]}}$

假设各测量误差是零均值，彼此不相关的高斯白噪声，对应于接收站距离和、角度测量以及站址标准差分别为σ_r∑，σ_θR，σ_s，则由式（1）求微分可得定位误差方程如下：

$ \left[\!\!{\begin{array}{*{20}{c}} {{\rm d}{r_{_\Sigma }}}\\ {{\rm d}{\theta _{_R}}} \end{array}} \!\!\right] \!= \!\left[{\begin{array}{*{20}{c}} {{c_{_{T1}}} + {c_{_{R1}}}}\!\!& \!\!{{c_{_{T2}}} + {c_{_{R2}}}}\\ {-\displaystyle\frac{{{{\sin }^2}{\theta _{_R}}}}{{y-{y_{_R}}}}}\!\!& \!\! {\displaystyle\frac{{{{\cos }^2}{\theta _{_{_R}}}}}{{x-{x_{_{_R}}}}}} \end{array}} \right]\left[{\begin{array}{*{20}{l}} {{\rm d}x}\\ {{\rm d}y} \end{array}} \right] \!\!+\!\! \left[{\begin{array}{*{20}{c}} {{k_{_T}} + {k_{_R}}}\\ {{k_{_{\theta, R}}}} \end{array}} \right] $

(3)

其中，${c_{_{i1}}} = \displaystyle\frac{{x - {x_{_i}}}}{{{r_{_i}}}} = \cos {\theta _{_i}}$ ， ${c_{_{i2}}} = \displaystyle\frac{{y - {y_{_i}}}}{{{r_{_i}}}} = \sin {\theta _{_i}}$ ，$\left\{ \begin{array}{l} {k_i} =-\left( {{c_{i{\rm{l}}}}{\rm{d}}{x_i} + {c_{i2}}{\rm{d}}{y_i}} \right), \left( {i = R, T} \right), \\ {k_{\theta, R}} = \frac{{\sin {\theta _R}}}{{{r_R}}}{\rm{d}}{x_R}-\frac{{\cos {\theta _R}}}{{{r_R}}}{\rm{d}}{y_R}。 \end{array} \right.$

式（3）写成矩阵形式为：

$ {\rm d}V = C{\rm d}X + {\rm d}{X_s}\text{，} $

(4)

其中：$\left| C \right| = \displaystyle\frac{{({c_{_{R1}}} + {c_{_{T1}}})\cos {\theta _{_R}}}}{{{r_{_R}}}} + \displaystyle\frac{{({c_{_{R2}}} + {c_{_{T2}}})\cos {\theta _{_R}}}}{{{r_{_R}}}}$, ${\rm d}V = {[{\rm d}{r_{_\Sigma }}, {\rm d}{\theta _{_R}}]^{\rm T}}$ ， ${\rm d}X = {[{\rm d}x, {\rm d}y]^{\rm T}}$ ， ${\rm d}{X_s} = {[{k_{_T}} + {k_{_R}}, {k_{_{\theta, R}}}]^{\rm T}}$ ， $C = \left[{\begin{array}{*{20}{c}}{{c_{_{T1}}} + {c_{_{R1}}}} & {{c_{_{T2}}} + {c_{_{R2}}}}\\{-\displaystyle\frac{{{{\sin }^2}{\theta _{_R}}}}{{{r_{_R}}}}} & {\displaystyle\frac{{{{\cos }^2}{\theta _{_R}}}}{{{r_{_R}}}}}\end{array}} \right]$ 。

则目标位置误差矢量可由式（4）得到

$ {\rm d}X = {C^{ - 1}}\left[{{\rm d}V-{\rm d}{X_s}} \right]\text{，} $

(5)

由上式可得：目标位置误差（dx，dy）与站址测量误差（dx_T，dy_T），（dx_R，dy_R）和测量误差（dr_∑，dθ_R）成线性关系。且仍为均值为0的高斯分布误差。

定位误差的协方差矩阵为：

$ \begin{array}{l} {P_{dx}} = E\left[{{\rm d}X{\rm d}{X^{\rm{T}}}} \right] = \\[7pt] \quad \quad {C^{ - 1}}\left\{ {E\left[{{\rm d}V{\rm d}{V^{\rm T}}} \right] + E\left[{{\rm d}{X_s}{\rm d}{X_s}^{\rm T}} \right]} \right\}{C^{ - {\rm T}}}{\text {，}} \end{array} $

(6)

$ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} \begin{array}{l} \sigma _x^2 = \displaystyle\frac{1}{{{{\left| C \right|}^2}}}\left[{{{\cos }^2}{\theta _R}(\sigma _{{r_\Sigma }}^2 + 2\sigma _s^2)/r_R^2 + } \right.\\[10pt] \quad \quad \quad \quad \left. {{{({c_{R1}} + {c_{T1}})}^2}(\sigma _{{\theta _R}}^2 + \sigma _s^2/r_R^2)} \right] \end{array}{{\text{，}}}\\[10pt] {\sigma _y^2 = \displaystyle\frac{1}{{{{\left| C \right|}^2}}}\left[{{{\sin }^2}{\theta _R}(\sigma _{{r_\Sigma }}^2 + 2\sigma _s^2)/r_R^2 + } \right.} \end{array}\\[10pt] \quad \quad \quad \quad \quad \left. {{{({c_{R2}} + {c_{T2}})}^2}(\sigma _{{\theta _R}}^2 + \sigma _s^2/r_R^2)} \right]{{\text{。}}} \end{array} \right. $

(7)

其中， $\left| C \right| \!=\! \displaystyle\frac{{({c_{R1}} \!+\! {c_{T1}})\cos {\theta _R}}}{{{r_R}}} \!+\! \displaystyle\frac{{({c_{R2}} \!+\! {c_{T2}})\cos {\theta _R}}}{{{r_R}}}$ 。

在二维平面内，定位精度的几何解释GDOP（Geometrical Dilution of Precision）为：

$ \begin{array}{*{20}{c}} \begin{array}{l} GDOP = \sqrt {\sigma _x^2 + \sigma _y^2} = \displaystyle\frac{1}{{\left| {1 + \cos \beta } \right|}}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad\\[16pt] \quad \quad \quad \quad \sqrt {\sigma _{{r_\Sigma }}^2 + 2\sigma _s^2 + 2(r_R^2\sigma _{{\theta _R}}^2 + 1)(1 + \cos \beta )} \end{array}\\[16pt] \begin{array}{l} = \displaystyle\frac{1}{{\left| {1 + \cos \beta } \right|}} \\[16pt] \quad \sqrt {\sigma _{{r_\Sigma }}^2 + 2\sigma _s^2 + 2r_R^2\sigma _{{\theta _R}}^2(1 + \cos \beta ) + 2(1 + \cos \beta )} \end{array}\\[16pt] \begin{array}{l} = \displaystyle\frac{1}{{\left| {1 + \cos \beta } \right|}} \\[13pt] \quad \sqrt {{c^2}\sigma _t^2 + 2\sigma _s^2 + 2r_R^2\sigma _{{\theta _R}}^2(1 + \cos \beta ) + 2(1 + \cos \beta )} {\text{。}} \end{array} \end{array} $

(8)

其中，σ_r∑=c·σ_t为接收站距离和测量标准差，c为声速，σ_t为接收站时延和测量标准差。σ_θR为角度测量标准差，σ_s为站址测量标准差。β=θ_R-θ_T为目标与发射站和接收站之间的夹角。r_R为接收站与目标之间的距离。

由上述分析可知，接收站的时延测量精度直接影响多基地声呐系统的定位精度。而准确测量目标模拟器的转发时延并对其进行补偿是提高接收站测量目标回波时延精度的关键。

1 目标模拟器基本框架^[4-6]

声呐目标模拟器主要是实现信号的接收、检测、存储及延迟转发的过程，框架如图 2所示，水听器采集接收信号放大一定倍数后AD采集由工控机实现信号的处理过程，在检测到信号的时候对接收信号进行存储并延迟转发由DA输出，经过一定倍数的放大，给发射换能器实现转发功能。

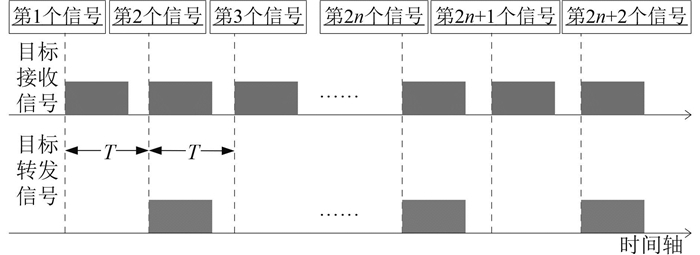
多基地协同探测中，主动声呐发送确知的周期信号，目标模拟器接收信号并在工控机内进行信号的检测，计算出信号的起始时刻后，目标模拟器截取信号部分，并在下一周期进行信号的转发，详见图 3。2个时间轴分别表示的是目标位置的接收信号和目标反射即转发信号来模拟目标的回波信号，设信号周期为T，目标模拟器接收第1个信号并检测到该信号，获取信号起始时刻位置并存储所需信号长度，以该起始时刻为基准延迟T即到达下一周期时将所存信号转发。

2 信号波形设计

为配合目标模拟器的信号检测，主动声呐发射波形设计为“头信号+主体信号”的形式，见图 4。头信号采用LFM信号，而主体信号可根据需要自行填充，头信号和主体信号之间有一定长度的间隔，实现对主体信号的保护。

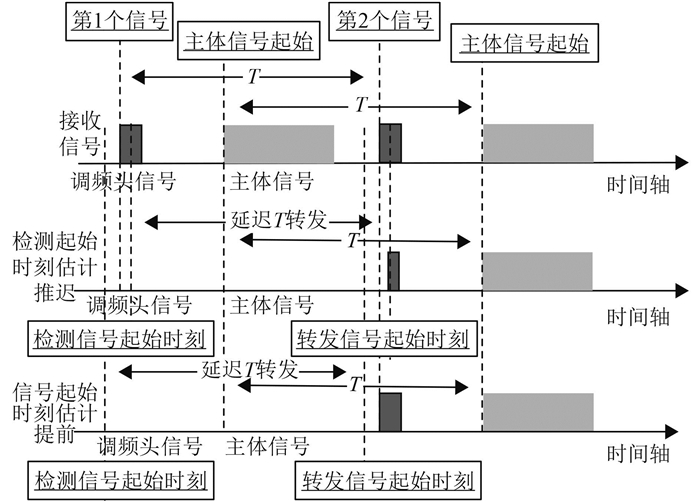
采用调频头加主体信号的形式的另一个优势是可以避免由于信号检测的对信号起始时刻的估计误差而带来的时延误差，见图 5。检测头信号并对其进行估计，当存在一定误差时，延迟T周期转发不变，带来的结果是头信号被截断或者超前转发，但对主体信号的时延不产生影响。从而解决了时延不精确的问题。

LFM信号的频率在脉冲宽度内与时间变化成线性关系。LFM信号的最大优点是匹配滤波器对回波信号的多普勒频移不敏感，即使回波信号具有较大的多普勒频移，采用原有的匹配滤器仍然能得到较好的脉冲压缩结果，因而可简化信号处理系统^[7]。因此，在本文中头信号采用线性调频信号。

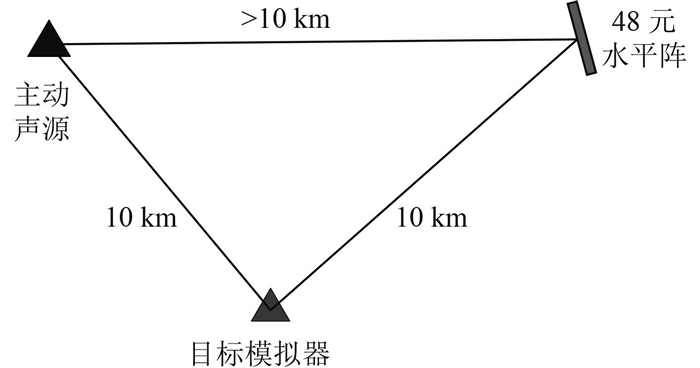
3 试验应用

在2015年12月使用目标模拟器代替真实的目标进行多基地协同试验，试验配置见图 6，主动声呐发射信号，目标模拟器接收并转发信号，而一条48元线阵水平布放在海底作为多基地声呐的接收站。其中主动声源与接收阵间距为12.1 km，与目标模拟器间距为9.8 km，而目标模拟器与接收阵间距为10.1 km。

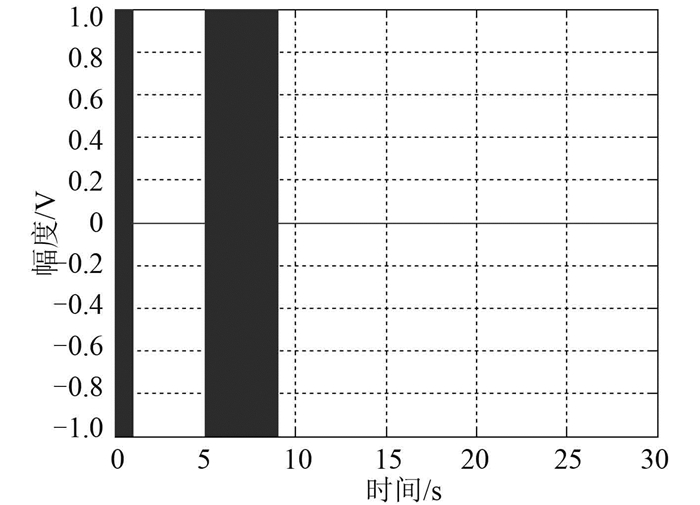
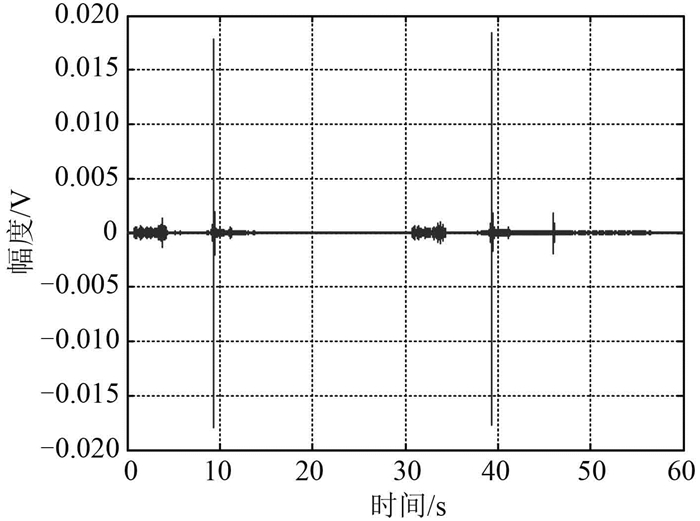
主动声呐发射信号波形见图 7，主动声呐发射信号周期为30 s，头信号为线性调频信号（脉宽为1 s，频带为1.5~2.5 kHz），头信号与主体信号间隔为4 s，主体信号也为LFM信号（脉宽为4 s，频带为1.5~2.0 kHz）。目标模拟器实际接收信号见图 8；而48元线列阵中某基元接收波形见图 9，滤波后可以看出直达波信号和转发信号；对主体信号进行时域相关结果见图 10，可以明显看出阵元接收直达波信号与转发信号匹配滤波峰值位置，即接收主体信号的起始时刻，通过直达波信号与转发信号的时差和它们之间距离信息进行对比，得到转发信号时延与理论值偏差30 ms左右。试验结果表明目标模拟器能够产生回波信号，实现模拟水下真实目标的功能，达到预期效果。

4 结语

本文主要研究多基地目标模拟器的波形设计方法，通过“头信号+主体信号”的方式设计主动声呐发射波形，可以实现目标模拟器对多种主体信号产生应答，并且目标模拟器对接收头信号的时延估计偏差不影响主体信号的转发时延。最后该目标模拟器及波形设计方法在海上试验进行了运用，能够满足多基地声呐探测的试验需求。