双层隔振可大大降低振动的传递,是隔离振动和结构噪声的有效措施。运用主动控制方法抑制振动的效果较好,对原结构改变不大,调节方便[1]。本文的目的是将双层隔振方法与主动控制技术相结合,探究双层主动控制实现方法。本文将在双层隔振主动控制模拟实验台架设计搭建及其误差通道辨识的仿真和实验方面开展一系列工作。
1 双层隔振主动控制模拟实验平台的设计及搭建本文所设计的双层隔振模拟实验平台如图 1所示,双层隔振系统的上层质量代替船舶主机,次级振源安装在第2层。双层模拟实验平台上层质量为0.56 kg,下层质量为5.6 kg。上层质量用30 mm×40 mm四个橡胶隔振器,均匀排列支撑。而第2层质量用50 mm×40 mm四个橡胶隔振器均匀排列支撑。

|
图 1 双层隔振主动控制实验平台 |
参考隔振原理及各种隔振器的性能特点,本实验选用橡胶隔振器对称布置在2层平台之间。在上层与第2层中间采用30 mm×40 mm VD型橡胶隔振器,第2层与底层中间采用50 mm×50 mm VD型橡胶隔振器,每层使用4个橡胶隔振器以主惯性轴对称分布。在实验过程中,橡胶隔振器承担实验平台的重量,并减弱振动源向底层基座传递的振动,尤其是传递的高频振动[2]。本试验台架的附属机构均采用对称布置,这样具有良好的解耦效果,并且简化设计难度。
分析计算表明,执行器的优化配置与系统的可控性条件紧密相关,执行器应布置在系统振动变形最大的地方。但是执行器不能位于或接近被控模态的节点或节线处,否则控制效果不理想,并且每个被控模态均需对应的执行器才能保证都能被有效控制。
本文中实验平台有3个被控模态,3个被控模态至少安装3个执行器。这时执行器的效率最大。但考虑到模拟实验平台有4个橡胶隔振器,为了便于系统调整,将垂直方向的执行器与每个橡胶隔振器作为一组,并平行安装。因而,在垂直方向就需要4个执行器。考虑到本实验台架的实际尺寸情况,将4个执行器分别对称放置在四角上。
与执行器的配置类似,传感器的位置和数量会影响最后的控制效果。如果传感器位于或者接近被控模态的节线处,将所测到的信噪比很差,无法正确反映所测平台整体的振动情况,因而也不可控。所以要对传感器的位置和数量进行优化配置。
由于所研究的双层隔振主动控制模拟实验平台只研究其垂直方向的振动,只研究其中3个被控模态,所以至少需要3个传感器才能使每个被控模态可观、可控,为了与4个执行器配合本文选取4个传感器。4个传感器应远离被控模态振型的节点或者节线,否则无法准备反映平台的振动情况。
2 滤波x-LMS算法及仿真基于LMS算法的自适应控制被广泛用于声、振的主动控制的实验和实践中。LMS算法通过采用误差信号单个样本方差的负梯度代替均方误差的负梯度来调节滤波器的权值,使二次性能指标到达最优。然而在实际应用中不可避免有误差通道的存在,如果采用标准的LMS算法,最后结果对性能函数负梯度的估计会不准确,权向量的调整没有按照理想的方式进行,因此我们引入x-LMS算法,滤波x-LMS算法的主动控制系统如图 2所示。

|
图 2 单通道滤波x-LMS算法的主动控制系统示意图 |
滤波x-LMS算法过程为:
| $ \left\{ \begin{array}{l} y(n) = {W^{\rm {\rm T}}}(n)W(n)\text{,}\\ e(n) = d(n) - S(z)\left[ {{W^{\rm T}}(n)X(n)} \right]\text{,}\\ W(n + 1) = W(n) + 2\mu e(n)\left[ {S(z)X(n)} \right]\text{。} \end{array} \right. $ | (1) |
性能函数为:
| $ J = E\left\{ {\sum\limits_{j = 1}^j {e_j^2(n)} } \right\} = E\left\{ {{e^{\rm T}}(n)e(n)} \right\}\text{,} $ | (2) |
以二执行器,二误差传感器为例,考虑到误差通道的耦合情况,流程图如图 3所示。
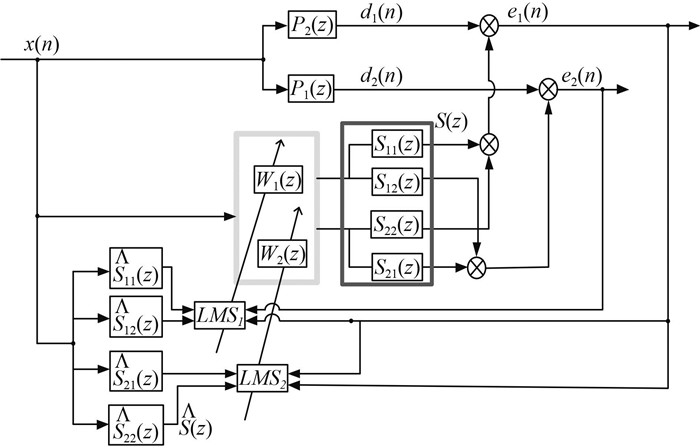
|
图 3 多通道滤波x-LMS算法的主动控制系统示意图 |
其x-LMS算法公式可推导为:
| $ \left\{ \begin{array}{l} {y_1}(n) = \sum\limits_{i = 0}^{L - 1} {{w_{1,i}}x(n - l)}\text{,} \\ {y_2}(n) = \sum\limits_{i = 1}^{L - 1} {{w_{2,i}}x(n - l)}\text{,} \end{array} \right. $ | (3) |
| $ \left\{ \begin{array}{l} {e_1}(n) = {d_1}(n) - \sum\limits_{i = 1}^2 {C_{i = 1}^{\rm T}{Y_i}(n)} \\ = {d_1}(n) - \left[ {C_{11}^{\rm T}{Y_1}(n) + C_{21}^T{Y_2}(n)} \right]\text{,}\\ {e_2}(n) = {d_2}(n) - \sum\limits_{i = 1}^2 {C_{i = 2}^{\rm T}{Y_i}(n)} \\ = {d_2}(n) - \left[ {C_{12}^{\rm T}{Y_1}(n) + C_{22}^T{Y_2}(n)} \right]\text{,} \end{array} \right. $ | (4) |
| $ \left\{ \begin{array}{l} {W_1}(n + 1) = {W_1}(n) + \mu \sum\limits_{j = 1}^2 {{{X'}_{1j}}(n){e_j}(n)} \\ = {W_1}(n) + \mu \left[ {{{X'}_{11}}(n){e_1}(n) + {{X'}_{12}}(n){e_2}(n)} \right]\text{,}\\ {W_2}(n + 1) = {W_2}(n) + \mu \sum\limits_{j = 1}^2 {{{X'}_{2j}}(n){e_j}(n)} \\ = {W_2}(n) + \mu \left[ {{{X'}_{21}}(n){e_1}(n) + {{X'}_{22}}(n){e_2}(n)} \right]\text{。} \end{array} \right. $ | (5) |
| $ \begin{array}{l} {{X'}_{ij}}(n) = {\left[ {{{x'}_{ij}}(n),{{x'}_{ij}}(n - 1), \cdots ,{{x'}_{ij}}(n - L + 1)} \right]^{\rm T}}\text{,}\\ {{x'}_{ij}}(n) = \sum\limits_{h = 0}^{H - 1} {{c_{ij,h}}x(n - h)} \text{。} \end{array} $ | (6) |
性能函数为:
| $ J = E\left\{ {\sum\limits_{j = 1}^j {e_j^2(n)} } \right\} = E\left\{ {{e^{\rm T}}(n)e(n)} \right\}\text{。} $ | (7) |
利用Simulink软件对两执行器两误差传感器,利用x-LMS算法的主动控制进行仿真,模型如图 4所示。图 5和图 6为仿真结果。

|
图 4 Simulink仿真模型 |
由图 5和图 6的仿真结果可知,在合理的范围内,适当增加步长μ值,其误差值在实验允许的范围内趋于稳定。

|
图 5 滤波器长度均为64阶,仿真停止时间设置为20 ms误差图 |

|
图 6 仿真停止时间设置为200 ms误差图 |
为验证所搭建的双层隔振主动控制实验台架的实用性,及优化理论分析的合理性,本文进行不同频率下的单通道误差通道辨识实验。
实验过程使用的实验设备如下:1)电磁式执行器1台,在通道辨识过程中作为激振器使用;2)加速度传感器1个,测量平台振动信号传给pulse机;3)功率放大器1台,连接在信号发生器与执行器之间,用于放大信号发生器产生的信号;4)信号发生器1台,发出不同频率的振动信号;5)示波器1台,分别与信号发生器和传感器连接,用来监测信号;6)多通道pulse机1台并配以相应的计算机pulse软件,取一通道与信号发生器连接,取另一通道与传感器连接,并将两路信号传输进计算机。

|
图 7 实验设备 |
实验过程如下:根据上述优化布置安置好各实验设备(见图 7),并根据图 8连接各个实验装置。先用信号发生器产生一组正弦信号,经功率放大器进行功放,驱动电磁式执行器产生激振力。信号发生器产生的信号同时输入pulse机中,作为LMS算法的输入信号。加速度传感器采集到的信号输入pulse中,作为LMS算法中的期望信号。然后,调节计算机中pulse软件的相应参数,导入2组信号,观测接受信号图象并生成输入信号数据和期望信号数据。最后将获得的数据导入到Matlab中进行数据处理,利用LMS算法得到误差值及权函数,误差在可接受范围,误差通道辨识实验完成。
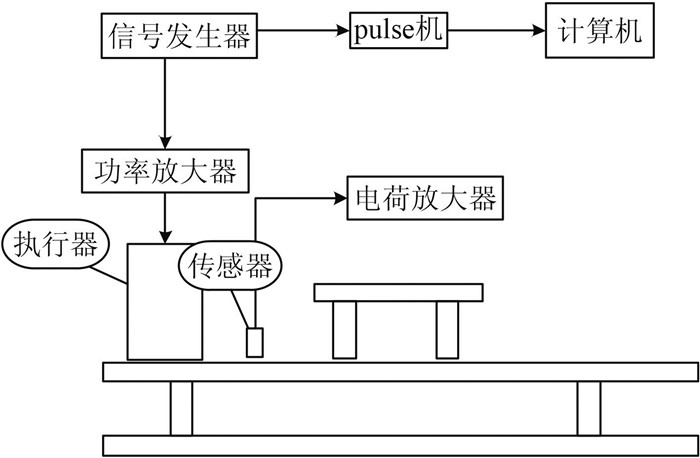
|
图 8 实验设备 |
改变信号发生器的频率,分别产生40 Hz和50 Hz的正弦激励信号,激励信号通过功率放大器进行功放,驱动电磁式执行器产生激振力。在误差通道阶数为128阶的情况下,得出以下实验结果,如图 9所示。

|
图 9 128 阶时不同频率下响应 |
不同频率下的通道辨识实验,误差信号波动均能收敛在理想范围内,如图 9(c),并得到较为理想的正弦函数权值,如图 9(d)。通过比较不同频率下的误差信号波动图像可知,随着频率增大,误差信号更为收敛,所得权函数更为准确。40 Hz时的信号波动较为强烈,可以估计出测试点的模态在40 Hz附近,本文不做过多讨论。实验证明本文所设计的控制系统通道辨识误差收敛在实验允许范围,能够满足主动控制系统的要求。
4 结语本文为深入的探究振动主动控制实现方法,通过查阅相关文献综合各种理论的优化方案,设计并搭建了双层隔振主动控制实验模拟台架。该实验台架的搭建综合考虑了实验台架耦合性及传感器、执行器的优化布置等方面,较为符合实际的振动环境并对控制方式有所完善,具有潜在的应用价值。试验台架结构紧凑,对模拟振动环境探究振动控制较为适宜。此试验台架的搭建完成为后续的实验工作打下了良好的基础。
本文实现了双通道双传感器的滤波x-LMS算法仿真,仿真结果误差综合考虑收敛性和稳定性,通过适当调整μ值,使其在实验可接受范围。仿真结果表明,双通道主动控制实现较为理想。
本文对所搭建的试验台架进行了误差通道辨识,结果较为理想。由于时间关系,本文未对所搭建实验台架进行主动控制实验探究,作者将在后续工作中完成。
| [1] | 高宏伟, 罗军, 贾建援. 双层隔振系统主动控制的建模与仿真[J]. 机械科学与技术 , 2005, 24 (11):1340–1342. |
| [2] | 梁威, 杨青芳, 薛丹, 等. 减震用橡胶材料及其应用[J]. 合成橡胶工业 , 2006, 29 (4):313–316. |
| [3] | 史晔.基于内模型控制算法的主动消振技术研究[D].哈尔滨:哈尔滨工程大学, 2013. |
| [4] | 严超.基于电动式作动器的主动消振技术研究[D].哈尔滨:哈尔滨工程大学, 2007. |
| [5] | 赵利颇.基于DSP的电磁作动器控制系统研究[D].石家庄:石家庄铁道学院, 2006. |
| [6] | 刘艳, 刘贵杰, 刘波. 传感器优化布置研究现状与展望[J]. 传感器与微系统 , 2010, 29 (11):4–6. |
 2016, Vol. 38
2016, Vol. 38
