相对于传统油液压系统而言,水液压技术因其独有的优势而越来越受到人们的重视[1 -2],而水液压阀则是其关键。在水液压系统中使用传统的液压阀时,总会有一些问题出现[3],之前相关的研究大多将侧重点放到气蚀对阀口处的损害,而高速液体携带的杂质对液压阀的冲蚀[4 -6]往往被忽略,因此本文将对水液压阀中的两相流侵蚀进行了仿真与分析。阀口附近的流场分析用到了全气蚀模型[7],并且建立了相应的粒子运动模型方程和冲蚀模型方程,进而通过FLUENT将液压阀口处的冲蚀、气蚀模型进行仿真,并且将气体体积百分比和冲蚀率计算出来。
传统的防气蚀方法主要用到如增加多级节流口、分级减压法和将特殊防侵蚀材料用到阀口处[3],而由于水液压系统中复杂的两相流环境,这些方法对降低水液压气蚀、冲蚀效果并不明显。考虑到红柳树的生活环境以及对泥沙冲蚀的良好抗性[11],本文提出一种基于Bio-TRIZ理论[8 -10]而设计的新型水液压阀结构,该阀的阀芯表面上均布着一系列特殊沟槽,这样可以降低流经的水流速度,减少气蚀,并且能在附近形成局部紊流和涡旋,进而将水中的泥沙带走。
在设计过程中面临的问题是如何选择一种最合适的沟槽,这就要求对沟槽的尺寸和形状进行最优化求解,因此本文利用到ISIGHT软件[12],通过将冲蚀率和气蚀率分别设置为多目标函数中的的因变量,将沟槽的各个尺寸设置为自变量,建立一个完整的优化模型方程,并进行相应的求解。本文的Bio-TRIZ设计过程和优化求解方法在机械设计领域有着独特的创新性参考价值,并且对于仿生设计方向的拓展和延伸意义也不可小觑,可以作为对未来相关学科交叉领域的研究基础。
1 理论分析文中假定不可压缩气体的质量百分比已知,故采用由美国CFD Research Corporation的研究人员Singhal等提出的全气蚀模型(Full Cavitation Model)[7]。考虑水液压工况下湍流感应波动压力和不可压缩气体的因素,将水蒸汽发生率和可缩率的表达式进行修正如下
| $ {R_v} = {C_v}\frac{{\sqrt k }}{\sigma }{\rho _l}{\rho _{{v}}}\sqrt {\frac{2}{3}\frac{{({p_{sat}} - p)}}{{{\rho _{\rm{l}}}}}} \left( {{\rm{1 - }}{f_{{v}}}{\rm{ - }}{f_{{g}}}} \right),p<{p_{{{sat}}}}\text{,} $ | (1) |
| $ {R_c} = {C_c}{\rho _l}{\rho _v}\sqrt {\frac{2}{3}\frac{{\left( {p - {p_{{{sat}}}}} \right)}}{{{\rho _l}}}} {f_v},\;p > {p_{{{sat}}}}\text{。} $ | (2) |
式中:k为湍动能;σ为表面张力系数;ρV为液相密度;ρl为汽相密度;fV和fg分别为水蒸气和空气的质量分数;psat为已知温度下的液体饱和气化压力;经验常数Cv=0.02,Cc=0.01。
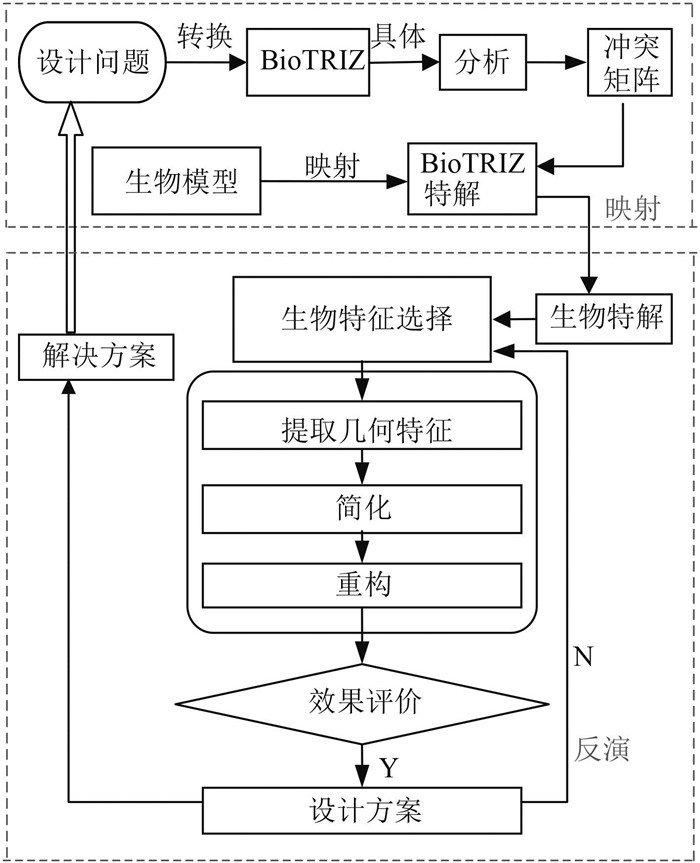
发明问题解决理论(TRIZ)是产品设计中常用的创新方法,Vincent等将其与仿生学相结合,提出了基于仿生学的设计方法:Bio-TRIZ理论[8],基于此,本文综合了关系-映射-反演原则[9]建立了仿生设计过程模型,如图 1所示。
|
图 1 基于BioTRIZ的仿生设计模型 Fig. 1 Bionic design process model based on BioTRIZ |
本文结合台湾国立成功大学的简燕辉所建造的生物实例资料库[10]进行生物实例搜索,选择红柳树作为防冲蚀设计的仿生学模型。
红柳树之所以能在沙漠中生长,抵抗风沙的侵蚀,因为树干表面上存在大量纵向分布的沟槽,这些沟槽形态各异,深度和宽度也不尽相同,这些沟槽不平行的表面结构能扰动流体流动,改变沙漠中风沙的运动状态,大大的提升其抗冲蚀性能,为了保证生物实例在设计过程中确实能够起到相应的仿生作用,现对仿生实例与设计目标进行相似性分析。相似性分析主要从功能相似性、结构相似性和边界条件相似性3方面进行。
利用仿生设计的相似性标准对红柳与设计目标的相似度进行计算,选取权重系数的评价因素集为U=[U1,U2,U3]=[功能,结构,边界条件]。基于评价因素集并结合判断矩阵标度及定度表格,得到判断矩阵M如下:
| $ M = \left[ {\begin{array}{*{20}{c}} 1 & 3 & 4\\ {1/3} & 1 & 2\\ {1/4} & {1/2} & 1 \end{array}} \right]\text{。} $ | (3) |
通过整理计算得到该矩阵的权重向量为
红柳树皮与设计目标的相似元相似度为:
红柳的树干表面上存在大量纵向分布的沟槽,这些沟槽形态各异,深度和宽度也不尽相同,如图 2(a)所示。通过观察红柳树皮的微观剖面,能看到红柳树皮表面分布着细密的沟槽,如图 2(b)所示。

|
图 2 红柳表皮上分布的纵向沟槽 Fig. 2 Structure of tamarisk epidermis |
因为气蚀和冲蚀都是水液压阀失效的原因[4 -6],在分析流场特性的时候,将用到CFD软件的RNGk-ε模型结合近壁面处理方法,结合气蚀模型、粒子运动模型及冲蚀模型分别计算气液平衡、粒子轨迹和冲蚀磨损率。
混合相的数值计算分3个部分:首先计算连续相的流场;其次在连续相流场稳定后加入离散相沙粒,对沙粒的运动轨迹进行跟踪;最后利用沙粒对近壁面的冲击反弹关系来计算它的磨损率。
用流体运动混合相连续性方程
流体运动混合相的动量守恒方程如下:
| $ \frac{\partial }{{\partial t}}\left( {\rho \mathop V\limits^{\rightharpoonup} } \right) + \nabla \left( {\rho \mathop V\limits^{\rightharpoonup} \mathop V\limits^{\rightharpoonup} } \right) = - \nabla P + \nabla \left[ {\mu \left( {\nabla \mathop V\limits^{\rightharpoonup} + \nabla {{\mathop V\limits^{\rightharpoonup} }^{\rm T}}} \right)} \right] - \mathop F\limits^{\rightharpoonup} \text{。} $ | (4) |
式中:
计算粒子运动及轨迹常用的方法为拉格朗日法(Lagrangian)。
考虑粒子扩散引起的湍流,粒子作用力平衡在笛卡尔坐标下的方程如下:
| $ \frac{{d\mathop {{u_p}}\limits^{\rightharpoonup} }}{{dt}} = \mathop {{F_D}}\limits^{\rightharpoonup} \left( {\mathop u\limits^{\rightharpoonup} - \mathop {{u_p}}\limits^{\rightharpoonup} } \right) + \frac{{\mathop g\limits^{\rightharpoonup} \left( {{\rho _p} - \rho } \right)}}{{{\rho _p}}} \text{,}$ | (5) |
| $ \left\{ \begin{array}{l} \mathop F\limits^ \rightharpoonup = \frac{1}{{\Delta V}}\sum {\left[ {\mathop {{F_D}}\limits^ \rightharpoonup \left( {\mathop {{u_p}}\limits^ \rightharpoonup - \mathop u\limits^ \rightharpoonup } \right)} \right]} {{\dot m}_p}\Delta t \text{,}\\ \mathop {{F_D}}\limits^ \rightharpoonup = \frac{{18\mu }}{{{\rho _p}d_p^2}}\frac{{{C_D}{R_e}}}{{24}}\text{。} \end{array} \right. $ | (6) |
式中:
当粒子穿过模型的控制体时,通过计算粒子的动量变化来求解连续相传递给离散相的动量值,其关系式为:
| $ F = \sum {\left[ {\frac{{18\mu }}{{{\rho _p}d_p^2}}\frac{{{C_D}{R_e}}}{{24}} + {F_o}} \right]} {m_p}\Delta t \text{。}$ | (7) |
其中Fo为其他外力,因为其影响不大可忽略。
冲蚀颗粒的属性可以直接设定,本文在数值模拟中选定为0.2 mm。沙粒冲击水液压阀腔内部材料表面时的能量损失,将使得反弹速度低于冲击速度,在研究中通常采用恢复系数来描述该作用,本文采用Forder A等[4]提出的的冲击反弹恢复系数公式:
| $ \!\left\{ {\begin{array}{*{20}{c}} \!\!\!\!\!\!\! {{e_N} \!=\! 0.998 \!-\! 0.78{\beta _1} \!\!+\! 0.19\beta _1^2 \!-\! 0.024\beta _1^3 \!+\! 0.027\beta _1^4}\text{,} \\[5pt] \!\!{{e_T} \!\!=\!\! 1 \!\!-\! 0.78{\beta _1}\!\!+\! 0.84\beta _1^2\! - \!0.21\beta _1^3 \!+\! 0.028\beta _1^4 \!-\! 0.022\beta _1^5}\text{。} \!\!\!\! \end{array}} \right.\!\!\!\! $ | (8) |
式中:eN为法向系数;eT为切向系数;β1为冲击角。冲蚀磨损率模型如下:
| $ {R_{erosion}} = \sum\nolimits_{p = 1}^{{N_p}} {\frac{{{m_d}C\left( {{d_p}} \right)f\left( \theta \right){v^{b\left( v \right)}}}}{{{A_{face}}}}}\text{。} $ | (9) |
式中:Rerosion为磨损率,md为颗粒质量;C(dp)为颗粒直径函数;f(θ)为冲击角函数;v为冲击速度;bv为速度函数;Aface为冲蚀面积。
2 仿真以及优化本文采将阀口开度与流量特性视为直线流量特性,其表达式如下:
| $ q = \frac{Q}{{{Q_{{\rm{max}}}}}} = \left( {1 - \frac{{{Q_{{\rm{min}}}}}}{{{Q_{{\rm{ma}}x}}}}} \right)\frac{L}{{{L_{{\rm{max}}}}}} + \frac{{{Q_{{\rm{min}}}}}}{{{Q_{{\rm{max}}}}}}\text{,} $ | (10) |
其中:Q为流量;L为阀口开度位置。
而水液压阀芯在某位置应该具有的开启截面积Ar可由流量系数Kv导出:
| $ {K_v} = \frac{{5.09A}}{{\sqrt {\left( {A/{A_r}} \right) - 1} }} \Rightarrow {A_r} = \sqrt {\frac{{K_v^2{A^2}}}{{{{5.09}^2}{A^2} + K_v^2}}} \text{。} $ | (11) |
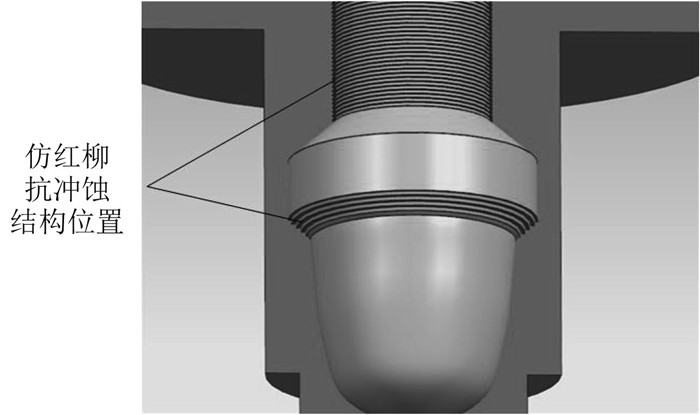
阀口在不同位置的开启横截面积可通过计算得出,文中最大可调位置时的流量系数Kv=2.0,Qmin=0.46 kg/s,Qmax=3 kg/s,建立的模型如图 3所示,抗冲蚀结构位于阀芯表面。
|
图 3 抗冲蚀结构在阀芯上的具体位置 Fig. 3 The anti-erosion structure of the valve core |
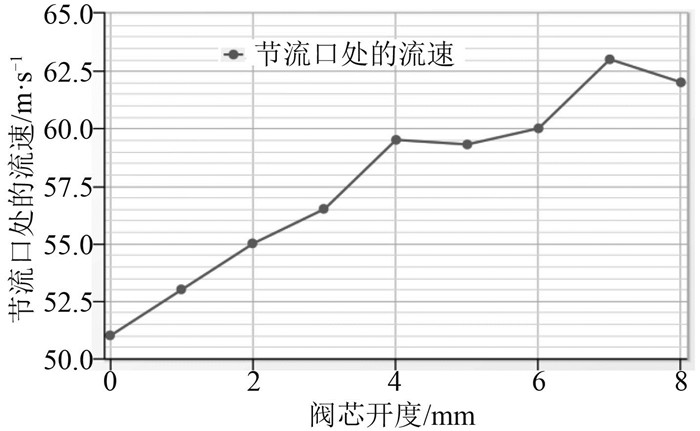
节流口处流体速度和对应的阀芯开度曲线如图 4所示,阀口的开度在7 mm处时的平均流速最大,对阀芯在此位置的模型进行相关的数值模拟。
|
图 4 阀节流处的速度随阀芯开度变化曲线 Fig. 4 The velocity-opening curve on valve orifice |
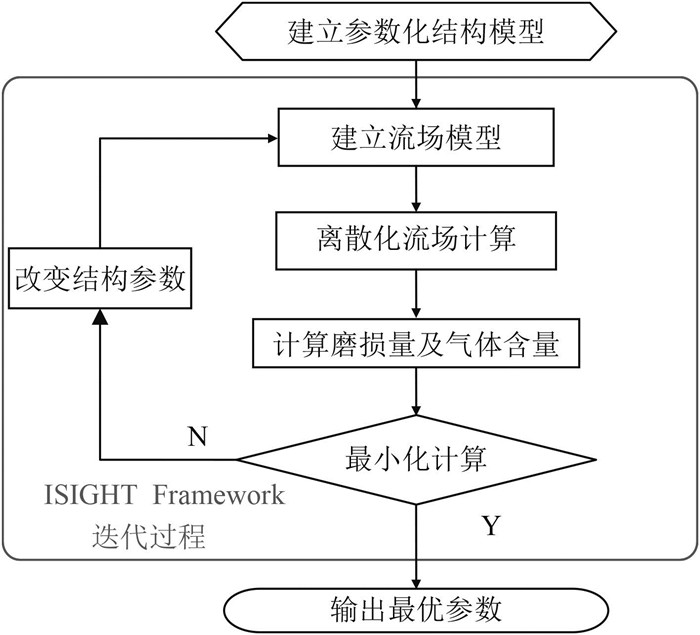
本文通过图 5所示的流程,使用ISIGHT优化软件,集成几何建模软件、网格划分软件和流体分析软件[12]。
|
图 5 抗冲蚀气蚀结构参数优化流程图s Fig. 5 Parameter optimization of anti-erosion structure |
设阀芯密封面处的冲蚀磨损率及气体体积百分比为目标函数,阀芯上沟槽尺寸作为复合自变量,数学表达式如下:
| $ \left\{ \begin{array}{l} X = \left[ {{s_i},{w_j},{t_k}} \right]{\text{,}}\\ {\rm{min}f}\left( X \right) = {\rm{min}}\left[ {{R_{erosion}}\left( X \right),{R_{cavitation}}\left( X \right)} \right]{\text{,}}\\ {\rm{s}}.{\rm{t}}.\:\:0.2{\rm{mm}} \leqslant {s_i} \leqslant 0.3{\rm{mm}},\:\left( {i = 1,2,3,4,5} \right){\text{,}}\\ 0.06{\rm{mm}} \leqslant {w_j}\leqslant 0.18{\rm{mm}},\:\:\left( {j = 1,2,3,4,5} \right){\text{,}}\\ 0.02{\rm{mm}} \leqslant {t_k} \leqslant 0.06{\rm{mm}},\:\:\left( {k = 1,2,3,4} \right){\text{。}} \end{array} \right. $ | (12) |
式中:Rerosion和Rcavitation分别为冲蚀率和气蚀率;si为每个槽的槽宽;wj为每个槽的槽深;tk为槽间距。需要优化的阀芯结构模型如图 6所示。
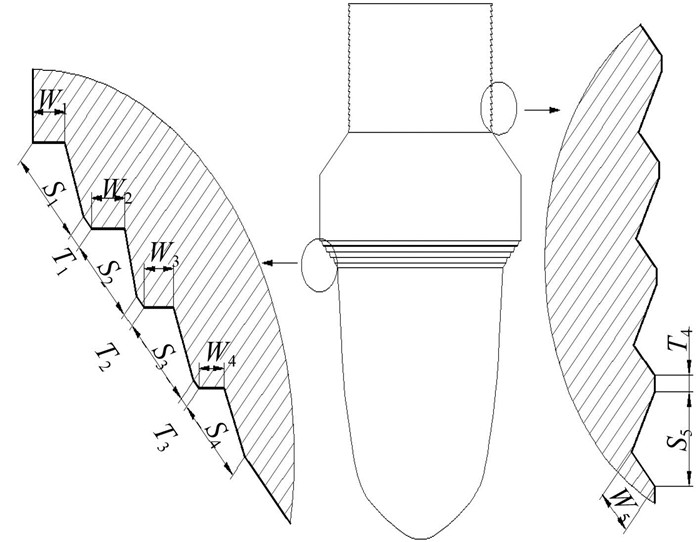
|
图 6 需要优化的锯齿形槽尺寸 Fig. 6 The groove structure |
本文使用最优拉丁超立方的试验方法对阀芯上的仿生型抗冲蚀结构参数进行分析[12],利用ISIGHT将几何建模软件UG、网格划分软件ICEM和数值模拟软件FLUENT集成在一起进行综合优化。最后得到优化后的仿生结构尺寸如表 1所示,经过优化后,冲蚀率为0.007 585 25 Kg/(m2s),较优化之前降低了77.34%(见图 7(a)),空化率为1.143 256%,较优化之前降低了36.15%(见图 7(b))。
|
|
表 1 优化后的结构尺寸 Tab.1 The bionic structure size after optimization |
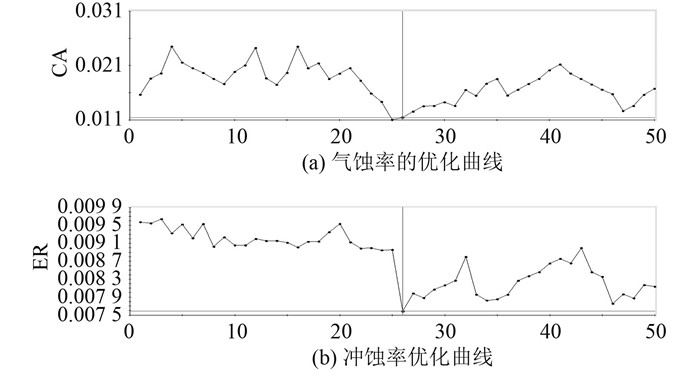
|
图 7 ISIGHT目标函数的气蚀率和冲蚀率优化历史 Fig. 7 Optimization of the objective function |
本文对水液压阀中的冲蚀-气蚀复合磨损进行了理论分析和仿真计算,并针对由此产生的液压阀失效结合Bio-TRIZ理论提出了一种解决方案,进而设计了一种模拟红柳树皮的仿生抗冲蚀水液压阀,对该阀的仿真流场分析可以看出,阀芯表面仿照红柳树皮的沟槽结构能够大大降低流经阀口的水的流速,减弱对阀的冲蚀。通过FLUENT软件对该仿生模型的气体含量和冲蚀率进行模拟分析,能够得到该阀内部磨损特性,另外通过ISIGHT对阀芯表面仿生沟槽尺寸的优化,构造一个以冲蚀、气蚀为因变量的多目标函数,经过计算后可以得到最优解,结果显示该仿生型水液压阀的气蚀率和冲蚀率被大大降低。
| [1] | URATA E. Technological aspects of the new water hydraulic[C]//Proceedings of the sixth Scandinavian International Conference on Fluid Power. Tampere, Finland:[s.n.], 1999:21-34. |
| [2] | VARANDILI E. Properties of tap water as a hydraulic pressure medium[C]//Proceedings of the sixth Scandinavian International Conference on Fluid Power. Tampere, Finland:[s.n.], 1999:113-127. |
| [3] |
弓永军.纯水液压控制阀关键技术研究[D].杭州:浙江大学, 2005:23-25.
GONG Yong-jun. Investigation into the key problems of water hydraulic control valves[D]. Hangzhou:Zhejiang University, 2005:23-25. |
| [4] | FORDER A, THEW M, HARRISON D. A numerical investigation of solid particle erosion experienced within oil field control valves[J]. Wear , 1998, 216 (2) :184–193. DOI: 10.1016/S0043-1648(97)00217-2 |
| [5] | BURAVOVA S N, GORDOPOLOV Y A. Cavitation erosion as a kind of dynamic damage[J]. International Journal of Fracture , 2011, 170 (1) :83–93. DOI: 10.1007/s10704-011-9604-z |
| [6] | GOHIL P P, SAINI R P. Coalesced effect of cavitation and silt erosion in hydro turbines-a review[J]. Renewable and Sustainable Energy Reviews , 2014, 33 :280–289. DOI: 10.1016/j.rser.2014.01.075 |
| [7] | SINGHAL A K, ATHAVALE M M, LI H Y, et al. Mathematical basis and validation of the full cavitation model[J]. Journal of Fluids Engineering , 2002, 124 (3) :617–624. DOI: 10.1115/1.1486223 |
| [8] | VINCENT J F V, BOGATYREVA O A, BOGATYREV N R, et al. Biomimetics:Its practice and theory[J]. Journal of the Royal Society Interface , 2006, 3 (9) :471–482. DOI: 10.1098/rsif.2006.0127 |
| [9] |
吉祥, 顾新建, 代风, 等. 基于BioTRIZ的产品创新设计过程[J]. 浙江大学学报(工学版) , 2014, 48 (1):35–41.
JI Xiang, GU Xin-jian, DAI Feng, et al. BioTRIZ-based product innovative design process[J]. Journal of Zhejiang University (Engineering Science) , 2014, 48 (1) :35–41. |
| [10] |
简燕辉.运用生物词汇结合仿生与TRIZ之绿色创新设计方法研究[D].台南:国立成功大学, 2013:49-78.
JIAN Yan-hui. Eco-innovative design method by integrating bionics with TRIZ through biological language[D]. Tainan:National Cheng Kung University, 2013:49-78. |
| [11] |
江佳廉.红柳抗风沙冲蚀机理及其仿生应用[D].长春:吉林大学, 2012:21-50.
JIANG Jia-lian. Anti-erosion mechanism of Tamarix Chinensis and its biomimetic application[D]. Changchun:Jilin University, 2012:21-50. |
| [12] |
赖宇阳.
ISIGHT参数优化理论与实例详解[M]. 北京: 北京航空航天大学出版社, 2012: 88-102.
LAI Yu-yang. ISIGHT parameter optimization theory and example explanation ISIGHT[M]. Beijing: Beihang University Press, 2012: 88-102. |
| [13] |
齐鄂荣, 曾玉红.
工程流体力学[M]. 武汉: 武汉大学出版社, 2005: 85-85.
QI E-rong, ZENG Yu-hong. Engineering fluid mechanics[M]. Wuhan: Wuhan University Press, 2005: 85-85. |
| [14] | YOSHIDA F, MIYAKAWA S. Dynamic characteristics of proportional control valve using tap water-experimental examination[C]//Proceedings of the twelfth Scandinavian International Conference On Fluid Power. Okinawa, Japan:[s.n.], 2011:18-20. |
 2016, Vol. 38
2016, Vol. 38
