2. 哈尔滨工程大学核科学与技术学院, 黑龙江 哈尔滨 150001
2. College of Nuclear Science and Technology, Harbin Engineering University, Harbin 150001, China
气泡广泛存在于核能、石油、化工、环境等工业过程。在船用核动力装置中,堆芯出口处、蒸汽发生器二回路侧都有大量的汽泡产生,气泡行为会影响系统的核、热特性,对系统安全性和可靠性至关重要。
对气泡上升运动的研究集中在气泡的速度、变形、脱离频率和受力分析[1 -3]。田恒斗[4]对气泡的上浮过程进行受力分析,得出了气泡瞬态加速度模型,结合流动传质边界层模型,依托非平衡传质理论,提出了气泡的瞬态非平衡传质模型。潘良明[5]从气泡受力平衡的机理出发,用VOF方法模拟了附加惯性力作用下竖直窄流道中气泡破裂的过程,分别对表面张力、附加惯性力大小及初始形状3个因素进行了讨论。以上学者的研究中,只关注了气泡在静水中的受力和运动状态,未考虑设备受外力而产生晃荡运动对气泡行为的影响,由于晃荡条件对气泡施加了附加惯性力,气泡的生长、脱离、上升规律都与静水中不同。强烈的晃荡运动还会引起一些重要设备如蒸汽发生器、冷凝器、除氧器的自由液面出现复杂变形及波动,包括驻波、行进波、水跃、组合波甚至漩涡、飞溅等甚为强烈的非线性现象[6]。这种情况下气泡的行为会极大地改变设备中流体流动和换热特性,因此需要对晃荡条件下气泡的运动状态进行分析。
本文研究依托晃荡实验台架,用高速摄影仪拍摄水箱内不同气流量下气泡的上升运动,得到晃荡2种工况下气泡的运动轨迹图和速度变化图。通过对气泡受力进行分析,阐述晃荡运动对气泡上升运动影响的机理。
1 气泡动力学基础假设气泡为球形刚体,不考虑多气泡间的相互作用,气泡在静水中受力可分以下几种[4]:
1)浮力FV 和重力FG
| ${{F}_{v}}=\frac{4}{3}{\rm{\pi }} {{R}^{3}}\rho {}_{l}\text{g}\text{,}$ | (1) |
| ${{F}_{G}}=\frac{4}{3}{\rm{\pi }} {{R}^{3}}\rho {}_{g}\text{g}\text{。}$ | (2) |
2)粘性阻力
| ${{F}_{D}}=\frac{1}{2}{{C}_{D}}{{\rho }_{l}}{\rm{\pi }} {{R}^{2}}{{v}_{b}}^{2}\text{。}$ | (3) |
式中:CD 为气泡上升的阻力系数; R为气泡半径,m;vb 为气泡的上升速度,m/s。
3)附加质量力
气泡在液体中上升时,会带动气泡附近的液体运动,这相当于增加了气泡的质量,带动这些液体所需要的惯性力叫做附加质量力,其表达式如下:
| ${{F}_{m}}=\frac{1}{2}{{\rho }_{l}}{{V}_{g}}\frac{{\rm d}{{v}_{b}}}{{\rm d}t}=\frac{2}{3}{\rm{\pi }} {{R}^{3}}{{\rho }_{l}}\frac{{\rm d}{{v}_{b}}}{{\rm d}t}\text{。}$ | (4) |
4)Basset力
在粘性流体中做加速运动的气泡,会受到一个瞬时的流动阻力,这个阻力与气泡的运动过程直接相关。
| ${{F}_{B}}=-6{{R}^{2}}\sqrt{{\rm{\pi }} {{\rho }_{l}}\mu }\int_{0}^{t}{\frac{{\rm d}{{v}_{b}}/{\rm d}\tau }{\sqrt{t-\tau }}}{\rm d}\tau\text{,} $ | (5) |
其中μ为液体动力粘度,Pa·s;Basset力的大小与气泡运动的历史有关。
上述均为气泡竖直方向受力。此外,由于气泡的变形运动,气泡在水平方向会产生压力梯度,气泡串中气泡的尾流也会影响到后续气泡的运动速度,在水箱按余弦规律横荡的情况下,气泡还会受到一个横向的惯性力,这个力可表示为:
| ${{F}_{e}}=-A{{\omega }^{2}}\cos (\omega t)\cdot \frac{4}{3}{{\rho }_{g}}{\rm{\pi }} {{R}^{3}}\text{。}$ | (6) |
其中A,
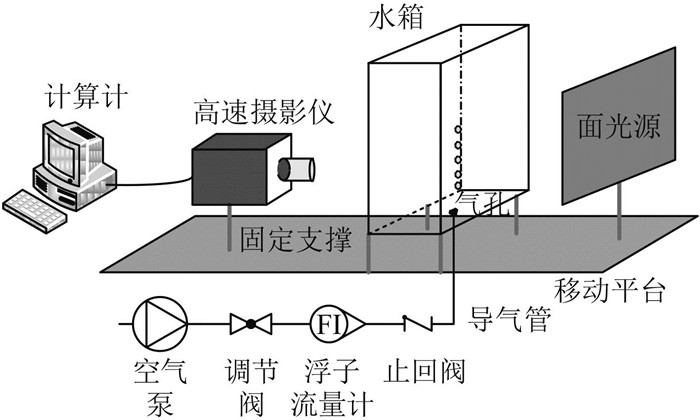
为研究晃荡条件下气泡的运动特性,设计并搭建了晃荡实验台,见图 1。实验装置包括玻璃水箱、步进电机、控制器、驱动器、移动平台、高速摄影仪和计算机等。
|
图 1 实验装置图 Fig. 1 Experimental apparatus |
1)运动系统:驱动器为步进电机供电并提供触发信号,步进电机带动丝杆正向或者反向转动,带动移动平台,使之横向移动。高速摄影仪、玻璃水箱和面光源通过固定装置与移动平台连接,以便使高速摄影仪能同步地拍摄水箱运动且图像的背景视野基本一致。控制器是一个有界面编程功能的单片机,可以设置步进电机转动的速度及方向,步进电机带动丝杆把旋转运动转化为水箱的平移运动, 使水箱在横荡条件下运行。晃荡的位移方程取余弦形式
| $x=A\cos (\omega t)\text{。}$ | (7) |
实验中晃荡幅度A取15 cm,晃荡周期T设定为为3.5 s。
2)供气系统:水箱底部装有可拆卸的气孔,气孔直径为1.5 mm;气孔通过导气管与气泵相连,管路中分别连接浮子流量计(测量范围16~160 mL/min)、流量调节阀和止回阀,这实现了不同流量下连续气泡的产生。
3)照明系统:为保证气泡图像与背景对比度明显、拍摄中背景亮度均匀一致,实验中采用40 cm × 40 cm的LED平面光源置于水箱背面,与高速摄影仪分列在水箱两侧;LED光源与移动平台固定,晃荡工况下能与水箱同步运动,保证了背景图象的一致性。
4)数据采集系统:移动平台上的高速摄影仪与水箱同步运动,同步拍摄气泡的运动图像,储存到摄影仪内部的存储器中。高速摄影仪可与计算机进行通信,通过PFV分析软件便可以实时地观测、分析气泡的运动,以调整至最佳的拍摄效果。实验中拍摄照片的分辨率为1024 × 512像素,拍摄速度选用1 000帧/s。
2.2 数据处理和误差分析采用Image Pro Plus(IPP)软件读入高速摄影仪拍摄的AVI格式视频,通过选取合适的灰度阈值,IPP自动识别气泡的边缘(要求图像中气泡与背景灰度差别明显)并追踪气泡的轨迹,如图 2所示。但是IPP只识别图像的像素位置,并不能确定具体距离,需要对图像进行尺寸标定。实验中气孔运圆柱体的直径为20 mm,以此为标尺,就得到气泡的相对坐标。数据处理时,将气泡刚出生时的位置作为坐标原点,气泡的瞬时速度计算公式为
| ${{v}_{xi}}=({{x}_{i+1}}-{{x}_{i}})/\Delta t\text{,}$ | (8) |
| ${{v}_{yi}}=({{y}_{i+1}}-{{y}_{i}})/\Delta t\text{。}$ | (9) |
式中i为气泡图片的帧序列号;

|
图 2 IPP识别的气泡运动轨迹(a)静止工况(b)晃荡工况 Fig. 2 bubble trajectory under stationary and sloshing condition in IPP software |
实验中浮子流量计为2.5级,即认为气泡的体积误差为2.5%,换算为气泡直径的误差为0.83%;标尺长度为20 mm,对应图像中标尺像素为93 pixels,故图像的缩放系数为0.215 mm/pixel。假设标定时的误差为为±1 pixel,则对于实验中一个直径5 mm的气泡,由误差传递公式计算实验测量误差为0.26 mm;高速摄影仪的曝光时间为10-6s,拍摄速率为1 000帧/s。对于速度为200 mm/s运动的气泡,图像处理时间每隔10帧保存1张图片。气泡在2张图片中的位置差为2 mm,而由于曝光时间造成的误差仅为2 × 10-4mm,相对于气泡位置测量误差可忽略不计,所以气泡的速度误差为26 mm/s, 在实验误差允许范围内。
3 实验数据分析 3.1 水箱静止条件下气泡的运动特性为研究晃荡运动对气泡行为的影响,首先在水箱静止工况下进行实验,记录气泡的上升轨迹和速度等参数,进而与晃荡条件下的实验结果进行对比。
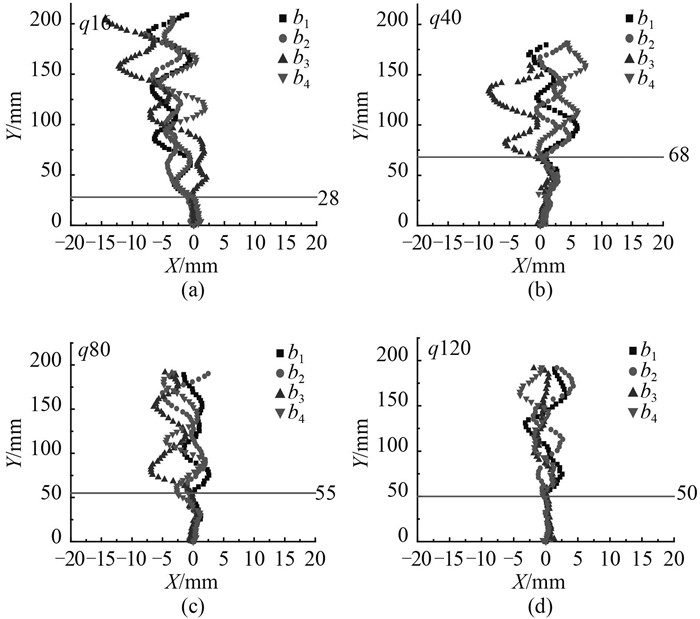
3.1.1 轨迹特性图 3展示了不同流量下气泡运动轨迹的变化规律,实验水位为25 cm,气孔直径1.5 mm,气流量为16~120 mL/min。b1,b2,b3,b4代表不同时刻生成的气泡。
|
图 3 不同流量时气泡运动轨迹(水箱静止) Fig. 3 Bubble trajectory of different gas flow |
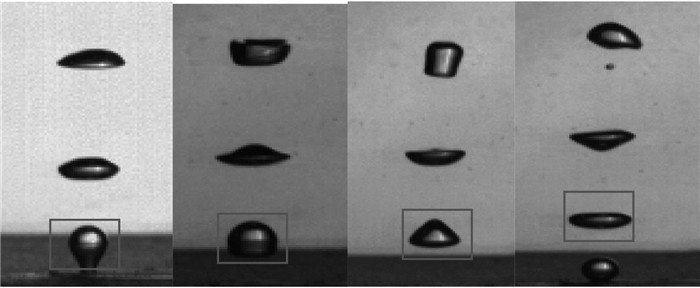
从图中可看出,在实验气流量条件下,水箱静止时气泡脱离气孔后都有一个近乎直线上升的阶段,随后气泡会在二维平面内摆动上升。由实验测量知,气泡直径随着流量的增加而增大,而“直线上升段”的距离先增加后减小(图中用与X轴的平行线标示了不同流量下气泡直线上升的距离)。这是由于气流量较小时气泡直径和脱离频率都很小,前一个气泡的尾流很难影响到随后的气泡,气泡的上升轨迹主要由气泡的变形情况决定,在气泡出生后很短的距离(不超过70 mm)内,气泡的运动就开始变得不稳定。实验中观察到,流量为40 mL/min时,气泡出生后,先由球形逐渐变为椭球形,然后变为扁平碟状;随后,椭球气泡的短轴突然拉伸,气泡形成一个柱状结构(见图 4)。随后气泡的变形和运动开始变得不规律。这个规律的变形阶段对应了图 3中所示的气泡的直线上升的直线段,这个阶段气泡只有竖直方向的变形,水平方向位移几乎为0。
|
图 4 静止工况下气泡产生后的形状变化 Fig. 4 Bubble shape change under stationary condition |
气泡未脱离气孔的时浮力与表面张力相等,受力平衡。气泡的颈部突然断裂后,气泡因受力不平衡开始加速,由于气体是可压缩的,气泡底部气体受表面张力作用先加速,气泡顶部气体从初速度0加速,上下表面速度不一致导致气泡被挤压。当气泡被挤压未扁平碟状时,气泡受到的浮力变小,气泡内气体压力大于气泡外压力,这个压差力使气泡突然拉伸,变为柱状。当气流量为16 mL/min时,气泡半径很小,气泡受力很快平衡,故其直线段相对较小。流量进增加到40 mL/min,气泡直径不太大,气泡变形慢,气泡串带动周围液体形成的带状流场对气泡的加速作用很明显,所以气泡可以稳定运动较长距离。当流量进一步增加时,气泡的直径快速增大,气泡变形更加剧烈,气泡运动轨迹越不稳定,故直线上升段的距离开始减小。
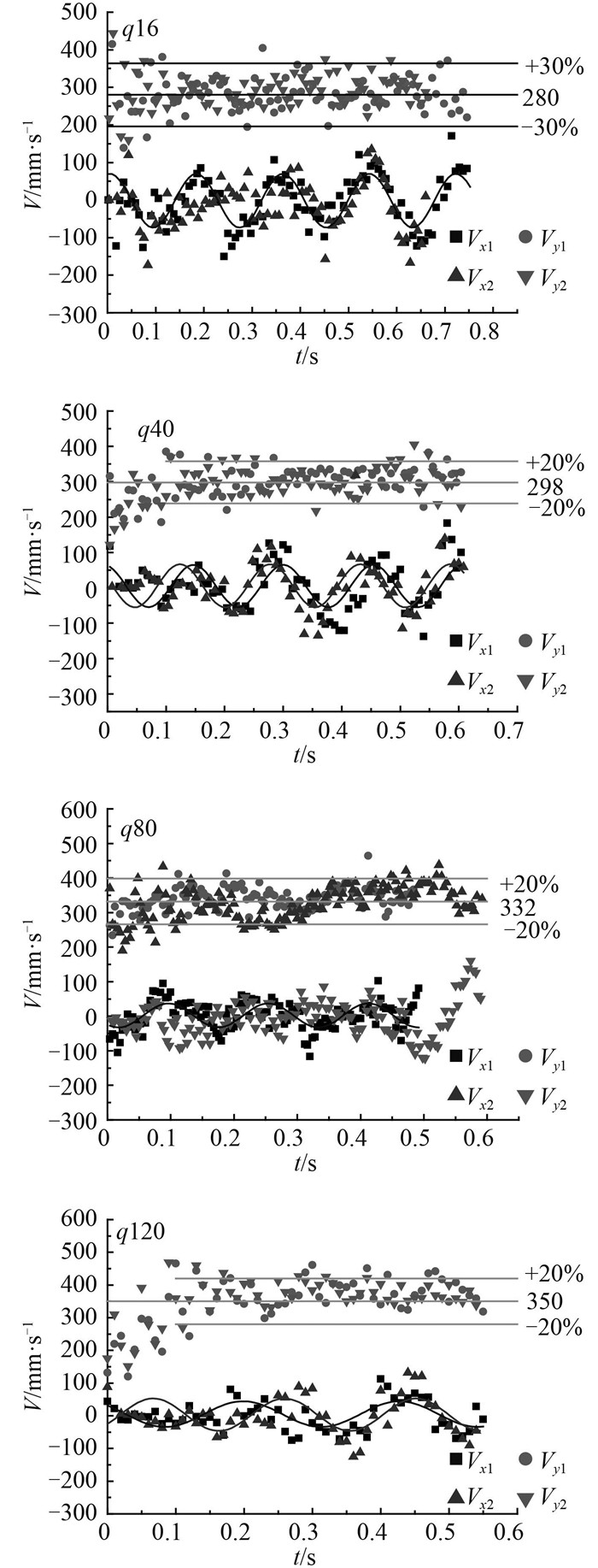
3.1.2 速度特性图 5展示了水箱静止时气泡运动的速度特征。Vx1,Vy1,Vx2,Vy2本别代表 2个不同时刻出生的气泡的水平方向和竖直方向的速度。分析知气泡竖直方向的速度在均值的20%~30%范围内上下波动,且气泡竖直方向速度随流量的增加而增大(实验流量范围内,气泡竖直速度从280 mm/s升高到350 mm/s);气泡体积越大,受到的浮力和流场的加速作用越明显,气泡受力平衡时,速度达到最大值,最大速度与阻力成正比,也就是与气泡直径正相关。
|
图 5 不同流量下气泡的速度(水箱静止) Fig. 5 Bubble velocity of different gas flow |
从图 5中可看出,随着气流量增加,气泡的竖直速度从0变化到平均速度需要的时间,时间也随之增长。文献[3]中推导了气泡加速时间的理论近似公式为:
| $t=\frac{4}{9\eta }{g}{{{r}}^{2}}{{\rho }_{\text{气}}}\text{。}$ | (10) |
式中:r为气泡半径;ρ气为气体密度;g为重力加速度。可知气泡加速时间与气泡直径的平方成正比,故气泡直径很小时,加速时间过短以至于在实验条件下难以监测。随着流量的增加,气泡直径也随之增大,由式(10)知,其加速时间变长,这与实验结果一致。
气泡水平方向速度呈正弦规律在均值0附近摆动,且摆动的周期随流量增加而增大。由文献[3]中的理论分析可知,
| ${{\omega }_{0}}\text{=}\sqrt{{k/ml}},\ \ \ \ \ T=2{\rm{\pi }} /{{\omega }_{0}}\text{。}$ | (11) |
式中:
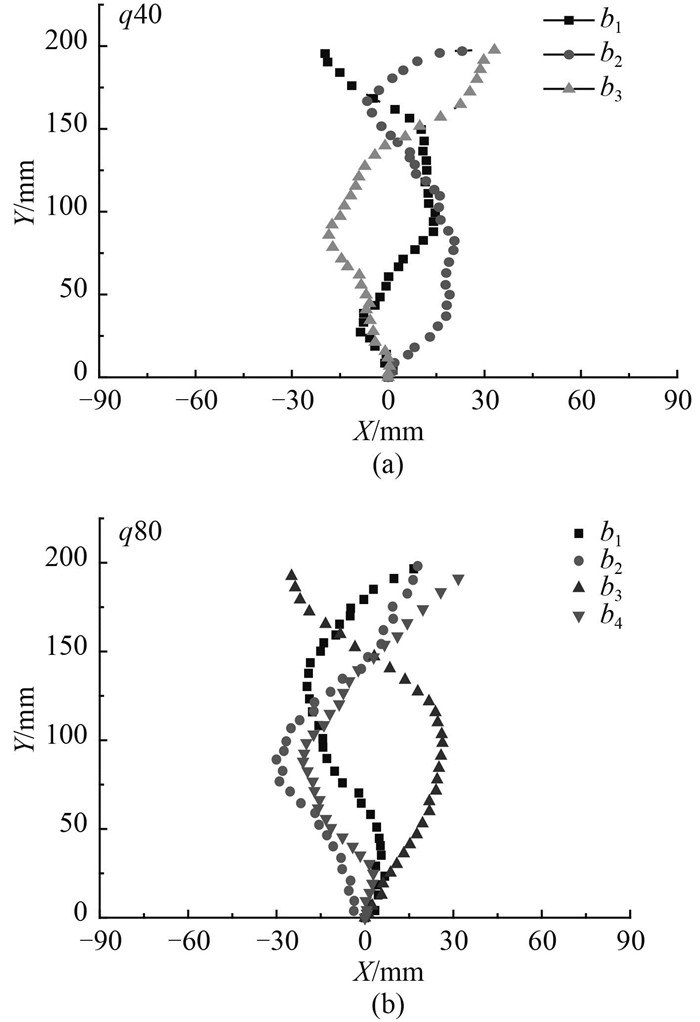
水箱横荡时产生气泡的运动轨迹如图 6所示,实验水位25 cm,晃荡周期为3.5 s,图中气流量分别为40 mL/min和80 mL/min,b1~b4代表在某晃荡周期内的不同时刻产生的气泡。
|
图 6 水箱晃荡时气泡运动轨迹图 Fig. 6 Bubble trajectory under sloshing condition |
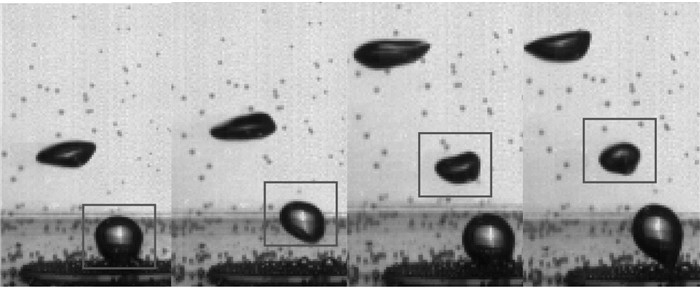
与水箱静止时的情况相比,气泡轨迹的直线上升阶段消失了,取而代之的是气泡串左右规律性的摆动,此时气泡出生后形状变化如图 7所示。由分析可知,气泡左右摆动的周期受到液面波动和水箱晃荡周期的共同影响。水箱横荡运动对气泡施加了水平惯性力,同时液面的周期性波动使水箱内压力和流场的分布更加复杂,故气泡不仅左右摆动幅度大大增加,而且在静止情况下近乎正弦上升的轨迹几乎消失的气泡跟随液面波动作大幅度的左右摆动。
|
图 7 静止工况下气泡出生后的形状变化 Fig. 7 Bubble shape change under sloshing condition |
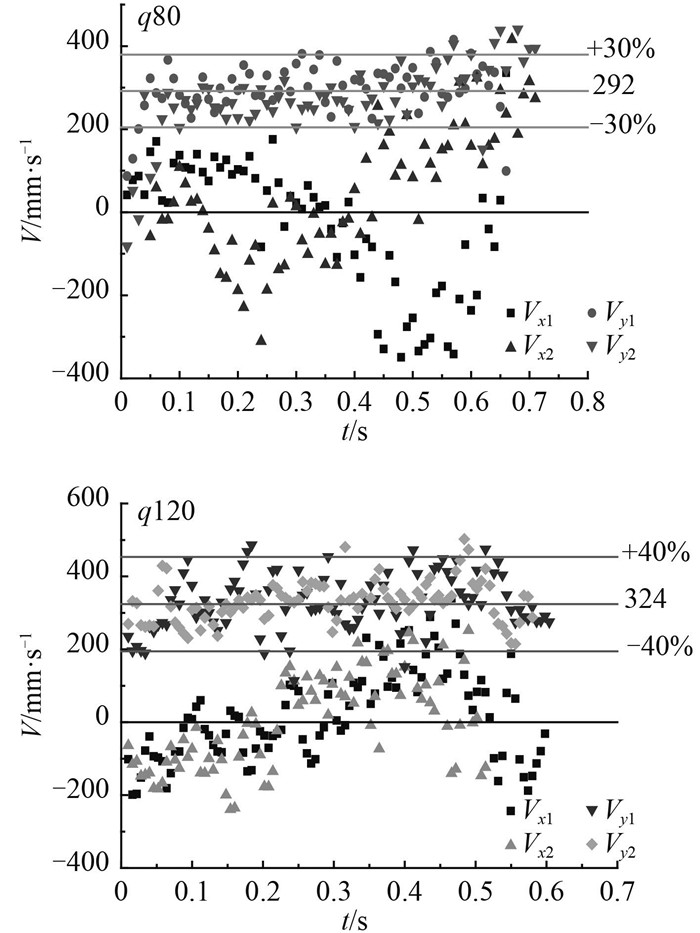
晃荡运动使得气泡受力情况变得复杂,导致气泡的速度特性与静止工况不同。图 8为晃荡周期3.5 s,气流量为80~120 mL/min时气泡的水平速度和竖直速度变化图。
|
图 8 晃荡周期为3.5 s时不同流量时气泡运动速度 Fig. 8 velocity of different gas flow (sloshing period is 3.5 s) |
表 1将晃荡和静止2种工况对应流量下气泡竖直速度和其波动范围进行对比,可以看出与静止工况相比,晃荡条件下气泡竖直方向的平均速度明显减小,竖直方向的速度在平均值附近波动的范围也相应增加。由于水箱横荡和液面的周期性波动,气泡变形更加复杂,由于气泡受到的粘滞阻力与气泡形状相关,故晃荡条件下气泡受到的粘滞力增加,导致气泡在竖直方向的平均速度减小。从图 6(b)可以看出晃荡运动还使得大流量(120 mL/min)时的加速段消失,晃荡运动使气泡出口处流场变得复杂,气泡加速度突变,气泡脱离气孔很短时间内就达到了平均速度的范围。
|
|
表 1 静止工况与晃荡工况气泡竖直方向速度对比 Tab.1 Bubble vertical velocity comparison in stationary and sloshing condition |
与静止情况相比,气泡由于受到液面波动的冲击,其水平方向速度除了自身的波动外,整体上在0附近大幅度摆动,这个摆动周期与液面的波动周期相同。静止状态下,气泡水平方向速度在0附近呈周期性的摆动,而在晃荡工况下,水平速度的周期性被破坏,取而代之的摆动是晃荡产生的附加惯性力以及液面波动造成的。
4 结语本文通过实验研究了静止和晃荡工况下矩形水箱内气泡的运动特性,分析得到了不同流量时气泡的运动轨迹、运动速度的变化情况,通过对气泡进行受力分析,解释了气泡运动参数变化的机理。得到了以下结论:
1)静止工况下气泡先直线上升后呈螺旋上升,随着流量增加,直线上升段长度先增加后减小。晃荡运动使气泡的直线上升段消失,气泡运动轨迹由螺旋上升改为大幅度摆动上升。
2)静止工况下,气泡由球形逐渐变为椭球形,然后变为扁平碟状;随后椭球气泡的短轴突然拉伸,气泡形成一个柱状结构,随后气泡开始螺旋上升,呈不规律变形;晃荡工况下,受附加惯性力影响,气泡的变形剧烈,加速时间变短。
3)与静止工况相比,晃荡运动产生的液面波动和横向力的共同作用,使气泡竖直方向速度减小,水平方向速度变化幅度变大,且变化频率与液面波动的频率一致。
本文的研究结果可为进一步研究晃荡条件下含有汽泡的两相流动设备的换热特性提供参考。
| [1] | BHAGA D, WEBER M E. Bubbles in viscous liquids:Shapes, wakes and velocities[J]. Journal of Fluid Mechanics , 1981, 105 :61–85. DOI: 10.1017/S002211208100311X |
| [2] | BOZZANO G, DENTE M. Shape and terminal velocity of single bubble motion:a novel approach[J]. Computers & Chemical Engineering , 2001, 25 (4/6) :571–576. |
| [3] |
潘守清, 欧阳俊. 气泡上升运动的观察与分析[J]. 武汉水利电力大学学报 , 1993, 26 (4):306–313.
PAN Shou-qing, OUYANG Jun. Observation and analysis of going-up movement of bubbles[J]. Journal of Wuhan University of Hydraulic and Electric Engineering , 1993, 26 (4) :306–313. |
| [4] |
田恒斗, 金良安, 丁兆红, 等. 液体中气泡上浮与传质过程的耦合模型[J]. 化工学报 , 2010, 61 (1):15–21.
TIAN Heng-dou, JIN Liang-an, DING Zhao-hong, et al. Coupling model for bubble rise and mass transfer process in liquid[J]. CIESC Journal , 2010, 61 (1) :15–21. |
| [5] |
潘良明, 张文志, 陈德奇, 等. 附加惯性力对气泡破裂的影响[J]. 核动力工程 , 2011, 32 (4):37–41.
PAN Liang-ming, ZHANG Wen-zhi, CHEN De-qi, et al. Effects of additional inertia force on bubble breakup[J]. Nuclear Power Engineering , 2011, 32 (4) :37–41. |
| [6] |
刘新立.船载液体晃荡载荷特性研究[D].武汉:武汉理工大学, 2009.
LIU Xin-li. The sloshing characteristics research of the liquid in ship tank[D]. Wuhan:Wuhan University of Technology, 2009. |
| [7] |
宋禹林.晃荡条件下气泡运动特性研究[D].哈尔滨:哈尔滨工程大学, 2014.
SONG Yu-lin. Research of rising bubble behavior in sloshing conditions[D]. Harbin:Harbin Engineering University, 2014. http://www.cqvip.com/QK/92273A/201506/665924127.html |
 2016, Vol. 38
2016, Vol. 38
