研究结构入水砰击问题最常用的二维模型是楔形体结构,陈震[1]对楔形结构在不同入水角度下的砰击问题进行研究,得到了压力峰值的变化规律。张健[2]考虑了气垫效应的影响,对砰击压力预报方法进行探究,得到了楔形体入水砰击载荷的预报公式。王珂[3]利用MSC.Dytran软件对LNG船的首部结构入水砰击过程进行了研究,探究结构曲率变化和入水速度变化对砰击压力的影响。
本文首先对二维楔形体的入水砰击过程进行数值模拟,分析入水过程中液面的变化和流场内物理量的变化,得到不同入水速度下楔形体上的砰击压力峰值与入水角度的关系。其次对三维刚性船舶尾部结构入水砰击问题进行研究,得到曲率变化对结构砰击载荷的影响规律。
1 二维楔形体结构入水砰击过程研究 1.1 有限元模型图 1为二维楔形体结构的有限元模型。楔形体结构x方向长度为0.4 m,高度为0.2 m,楔形体入水角β分别为1°~25°,结构距水面0.1 m。

|
图 1 典型楔形体有限元模型 Fig. 1 Finite element model |
图 2为楔形体入水砰击的计算模型。整个欧拉域水平方向范围为4.8 m,高度方向为3.7 m;其中空气域x方向长为4.8 m,高度方向为1.3 m,水域x方向长为4.8 m,高度方向为2.4 m。上部分欧拉区域为空气介质,采用理想气体本构单元,下部分欧拉区域为水介质,水域内的压力用多项式状态方程描述。在欧拉域的四周定义无反射边界条件。

|
图 2 典型楔形体有限元计算模型 Fig. 2 The calculation model |
对空气域和水域整个流场进行网格划分来描述材料间的流动,从而更真实地模拟流体运动。图 3为入水角度为15°的楔形体以10 m/s的均匀速度入水过程中欧拉域变化的情况。考虑到空气和重力情况下,自由液面变化情况与现有理论比较吻合。

|
图 3 自由液面的升高 Fig. 3 The elevation of free surface |
楔形体在入水砰击的过程中,流场内流体的物理量不断发生变化。当楔形体开始靠近水面时,空气的压力开始明显增加,出现较大的压力区域。随着楔形体结构入水角度的增加,砰击面上压力峰值以一定的速度沿着楔形面向上运动。
图 4为入水角为15°的楔形体以10 m/s均匀速度入水过程中的压力分布情况。压力波的位置基本上是位于喷射区的根部附近。
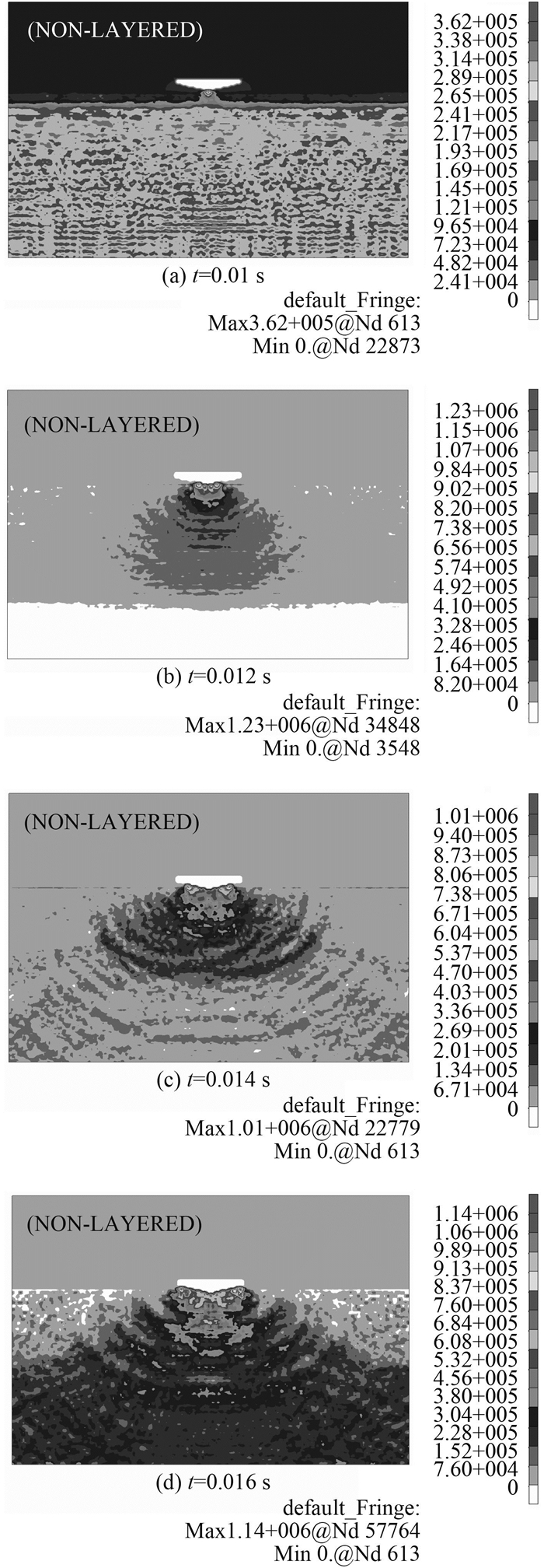
|
图 4 不同时刻流场内压力分布 Fig. 4 Pressure contour of the fluid field |
图 5为压力波传播速度与楔形体倾角的关系,其中VP是压力波在楔形体砰击面上的传播速度,Ve是楔形体等速入水速度。
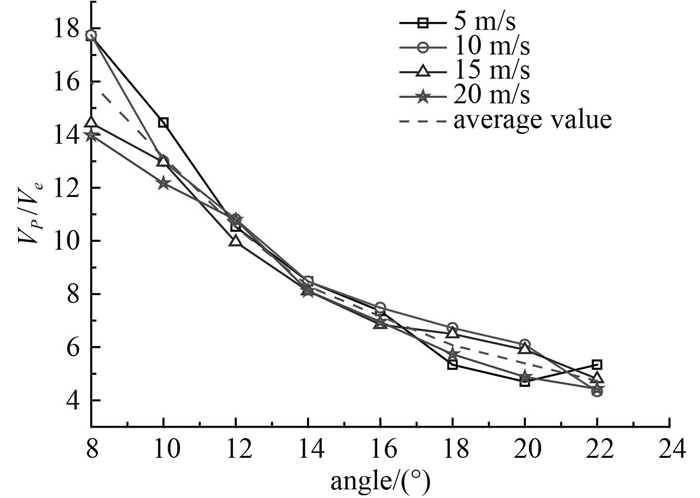
|
图 5 压力波传播速度曲线 Fig. 5 Velocity curve of the pressure wave |
图 6为入水角为15°的楔形体结以构15 m/s等速入水时结构附近流场速度矢量图。由图中可看到,气体流场的运动速度远大于水域流场的速度,并在其形体结构的边缘拐角处形成漩涡。

|
图 6 流场速度矢量图 Fig. 6 Velocity of euler elements |
根据冲量砰击理论,楔形体入水所受到的砰击压力峰值可以写成:
| $ {P_P}=k{\rho _w}V_n^2{。} $ | (1) |
式中:ρw为水的密度;Vn为楔形体砰击面的法相速度相对于水面的分量;k为楔形体入水砰击压力系数。
根据动力学原理,垂直于结构表面的速度沿水平面法向方向的速度分量才会产生冲击压力。如图 7所示,对于楔形体以速度Ve入水情况来说,相对速度为[5]:
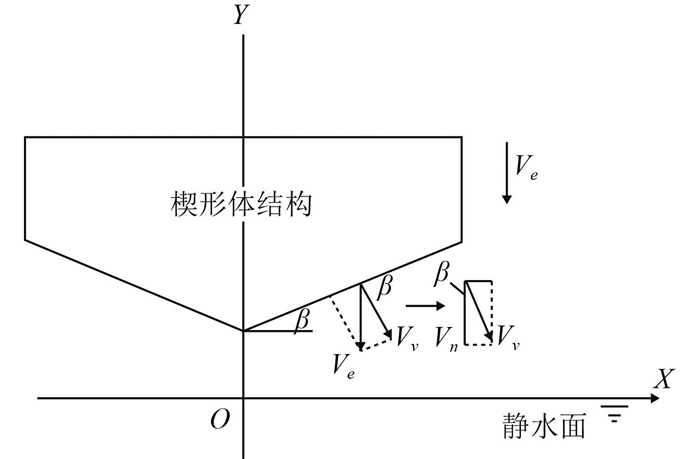
|
图 7 楔形体法向入水速度 Fig. 7 Normal velocity of the water entry |
| $ {V_n}={V_e}{\cos ^2}(\beta){,} $ | (2) |
将式(2)代入式(1),可得到砰击压力峰值为:
| $ {P_P}=k{\rho _w}{[{V_e}{\cos ^2}(\beta)]^2}=k{\cos ^4}(\beta){\rho _w}V_e^2{,} $ | (3) |
令
| $ {P_P}={k_1}{\rho _w}V_e^2{,} $ | (4) |
式中:系数k1为入水角度与冲击压力峰值的关系。
对不同倾角的楔形体以不同入水速度入水的k1值进行计算并与Chuang[6]试验结果相比较,如图 8所示。由图可知,中等速度入水时,k1曲线在结构的入水角2°~3°左右出现最大值,之后随着入水角度的增加而减小,在15°以后k1值变化区域平稳。k1值这种变化特点反映了当结构入水角度小于3°时,空气垫对冲击压力具有一定的影响。随着入水角度的增加,在结构边缘空气逃逸面积增大,空气比较容易从结构边缘处逃逸,空气垫的缓冲作用降低。虽然入水角度的增加有利于冲击压力的减小,但是整体上冲击压力有所增加。由于冲击压力为结构与水之间相互作用的动力效应,故随着结构入水角度的继续增加,空气层的影响较小。当入水速度为5 m/s和15 m/s时,数值模拟结果与试验结果吻合较好,入水速度为10 m/s和20 m/s,入水角度小于5°时,数值模拟结果要高于试验值,当入水角度大于5°时,2个速度下二者之间吻合较好。

|
图 8 不同速度下k1值曲线 Fig. 8 k1 curve at different impact velocity |
表 1为不同速度等速入水时不同倾角楔形体中间节点的压力峰值。由表可得,随着入水速度的增加,楔形体结构砰击面上的压力峰值增加,这主要是由于砰击压力峰值的大小与入水砰击速度平方成正比增加;随着楔形体结构入水角度的增加砰击面上压力峰值先增加再降低,最终趋于平缓。
|
|
表 1 不同速度入水时不同倾角楔形体的砰击压力峰值 Tab.1 The peak pressure with different inclination angles at different velocities |
船舶尾部结构包括水密横舱壁、水平桁、船底纵桁、舷侧外板、甲板、甲板横梁等等构件。尾部结构有限元模型如图 9所示。
|
图 9 尾部结构有限元模型 Fig. 9 Model of stern structure |
计算船舶尾部入水砰击过程时,刚性尾部结构恒速入水速度分别为5 m/s,10 m/s,15 m/s和20 m/s,三维流固耦合计算时间较长,因此本文在模拟三维模型入水砰击过程时,流场单位取模型尺寸的2~3倍,在边界上施加无反射边界条件,从而模拟无限水域情况,有限元计算模型见图 10。

|
图 10 有限元计算模型 Fig. 10 Calculation model |
船舶尾部结构入水过程中,水域液面受到尾部结构的挤压作用发生变形,入水砰击初始时刻,结构和水面之间的空气层随着结构被压入水中,空气垫的存在在结构和液面之间起到了缓冲作用,但对于船舶尾部结构型线变化比较大,横向斜率较大,尾部结构和水域之间的空气层将很快向四周超逸,因此对于船舶尾部结构空气垫的作用不是很明显。图 11和图 12为刚性尾部结构10 m/s入水过程中不同时刻横向和纵向液面的变化情况。

|
图 11 典型横剖面液面变化 Fig. 11 Liquid level in typical cross section |

|
图 12 中纵剖面液面变化 Fig. 12 Liquid level in middle longitudinal section |
为探究曲率对砰击压力的影响,对三维尾部结构在4种砰击速度下纵向和横向砰击压力分布进行了比较研究。
图 13为船舶尾部结构中纵剖面不同节点在4种砰击入水速度下砰击压力峰值。由图可以得到,随着船舶尾部结构入水速度的增加,结构上各个节点砰击压力峰值增加。由于尾部纵向曲率是逐渐减小,因此中纵剖面上砰击压力峰值随着纵向曲率降低砰击压力峰值呈增加趋势。
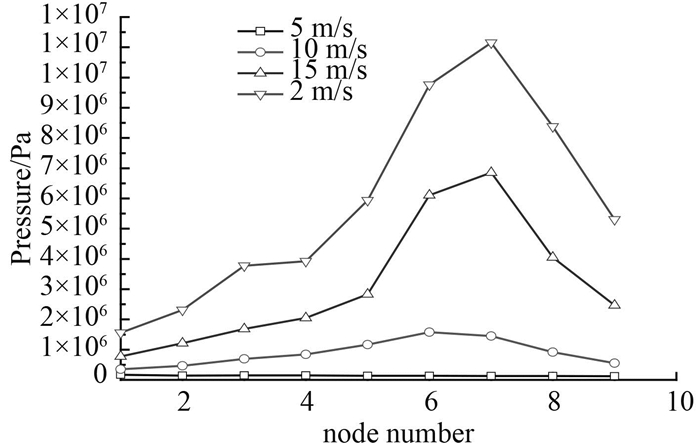
|
图 13 尾部压力峰值纵向分布曲线 Fig. 13 Pressure peak in longitudinal distribution |
图 14为3个典型横剖面上横向不同位置砰击压力峰值曲线。由于3个横剖面位置横向曲率变化规律的不同,因此3个剖面上砰击压力峰值趋势也是不相同的;对于船舶尾部FR2剖面曲率先增加后降低趋势,因此该剖面横向砰击压力峰值变化趋势为降低后增加;对于FR0和FR-2两个剖面横向曲率变化趋势近似为增加,因此该2个剖面的砰击压力峰值近似呈增加趋势。

|
图 14 尾部压力峰值横向分布曲线 Fig. 14 Pressure peak in transverse distribution |
本文对二维楔形体和刚性船舶尾部结构入水砰击过程进行了数值模拟研究,得到以下结论:
1)考虑流固耦合作用和重力等因素影响,给出了不同时刻二维楔形体结构考虑了空气和重力因素的液面升高的变化情况;
2)当入水速度为5 m/s和15 m/s时,二维楔形体结构入水砰击载荷的数值模拟结果与Chuang试验结果吻合较好,入水速度为10 m/s和20 m/s,入水角度小于5°时,数值模拟结果要高于试验值,当入水角度大于5°时,2种速度下二者之间吻合较好。
3)当楔形体入水角度增加时,结构砰击面上压力峰值的先增加再降低,最终趋于平缓。
4)三维结构横向和纵向的曲率对结构上的砰击压力峰值具有较大的影响,这主要是由于曲率的不同使得流场在曲率上的流动差异造成的。因此,在分析三维结构入水砰击问题时除了要考虑入水砰击速度不同之外,还要考虑结构曲率对砰击压力峰值的影响。
| [1] |
陈震, 肖熙. 二维楔形体入水砰击仿真研究[J]. 上海交通大学学报 , 2007, 41 (9):1425–1428.
CHEN Zhen, XIAO Xi. The simulation study on water entry of 2D wedge bodies[J]. Journal of Shanghai Jiaotong University , 2007, 41 (9) :1425–1428. |
| [2] |
张健, 尤恽, 王珂, 等. 基于气垫效应的二维楔形体入水砰击载荷预报方法研究[J]. 舰船科学技术 , 2016, 38 (3):7–12.
ZHANG Jian, YOU Yun, WANG Ke, et al. Prediction of the slamming pressure on a 2D wedge-shaped section based on the air cushion[J]. Ship Science and Technology , 2016, 38 (3) :7–12. |
| [3] |
王珂, 王志东, 米旭峰. LNG船三维首部结构入水砰击载荷数值研究[J]. 江苏科技大学学报(自然科学版) , 2012, 26 (3):218–221.
WANG Ke, WANG Zhi-dong, MI Xu-feng. Simulation of the slamming pressure of 3D bow construction for LNG carriers[J]. Journal of Jiangsu University of Science and Technology , 2012, 26 (3) :218–221. |
| [4] | OCHI M K, MOTTER L E. Prediction of slamming characteristics and hull responses for ship design[C]//Presented at Annual Meeting of SNAME 1973. New York:Society of Naval Architects and Marine Engineers, 1973, 81:144-177. |
| [5] | ZHAO R, FALTINSEN O M. Water entry of two-dimensional bodies[J]. Journal of Fluid Mechanics , 1993, 246 :593–612. DOI: 10.1017/S002211209300028X |
| [6] | CHUANG S L. Experiments on slamming of wedges-shaped bodies[J]. Journal of Ship Research , 1967, 11 (3) :190–198. |
 2016, Vol. 38
2016, Vol. 38
