0 引言

端部舱壁是潜艇耐压壳体的重要组成部分，需要有足够的结构强度来抵抗外部深水压力。端部舱壁从结构型式上可以分为平面舱壁和球面舱壁^[1]。随着潜艇大潜深的发展趋势，球面舱壁更能体现出结构重量轻、材料强度和布置空间利用率高等优势^[2]。本文将研究球面舱壁作为研究对象，分析其结构强度性能。

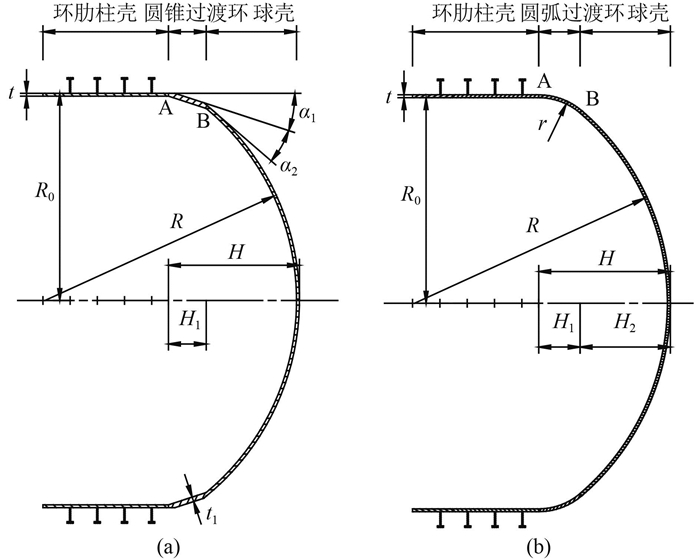
端部球面舱壁主要由球壳、过渡环和与过渡环连接的部分耐压柱（锥）体构成。由于首舱耐压船体为环肋圆柱壳，首舱壁中心线与耐压船体中心线重合，因此圆柱壳与球冠之间可采用轴对称过渡环连接，即整个球面舱壁为轴对称结构。过渡环形式可以分为锥壳过渡（采用厚板削斜连接）和圆环过渡，结构形式如图 1所示。

传递矩阵法^[3]是一种半解析半数值计算方法，适用于变截面厚度、结构不连续（斜率突变、加设肋骨等）的旋转组合壳结构强度计算，且便于结构参数分析。Riccati变换能将传统传递矩阵法的不稳定边值问题转化成稳定初值问题，且减小运算规模^[4]，具有计算稳定性好和精度高的优点。上述2种结构形式的球面舱壁均为轴对称旋转组合壳结构，因此Riccati传递矩阵法适合于球面舱壁结构强度计算。

本文采用Riccati传递矩阵法对2种舱壁结构进行强度分析。利用隐式Runge-Kutta方法离散舱壁结构微分控制方程，借助Riccati变换结合边界条件进行求解。借助Matlab编制传递矩阵法计算程序，利用程序对锥壳过渡形式、圆环过渡形式2种球面舱壁结构进行应力计算，分析应力强度性能及其差异。

1 Riccati传递矩阵法在球面舱壁结构应力计算中的应用

对旋转壳结构进行应力计算时，一般选取截面状态向量：

${\boldsymbol U}=\{u, w, {{\gamma }_{1}}, {{T}_{1}}, {{N}_{1}}, {{M}_{1}}\}{，}$

(1)

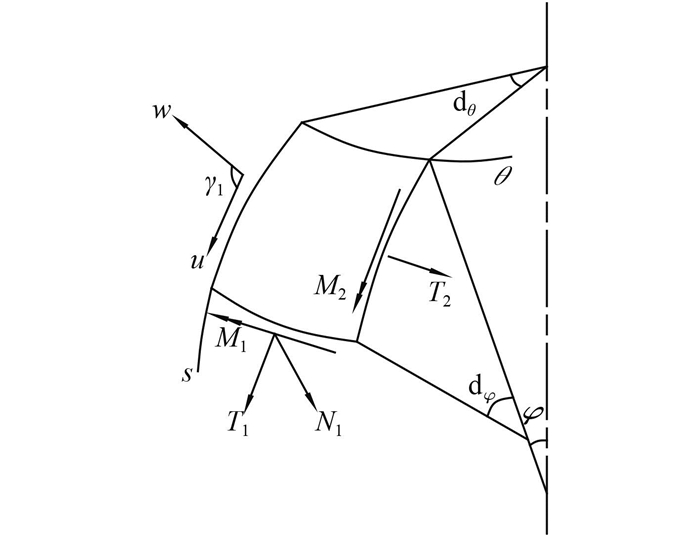
旋转壳状态向量及几何参数如图 2所示。由壳体理论推导出旋转壳结构状态向量关于弧长的一阶微分方程：

$\frac{\operatorname{d}}{\operatorname{d}s}{\boldsymbol U}={\boldsymbol A}\cdot {\boldsymbol U}+{\boldsymbol C}{。}$

(2)

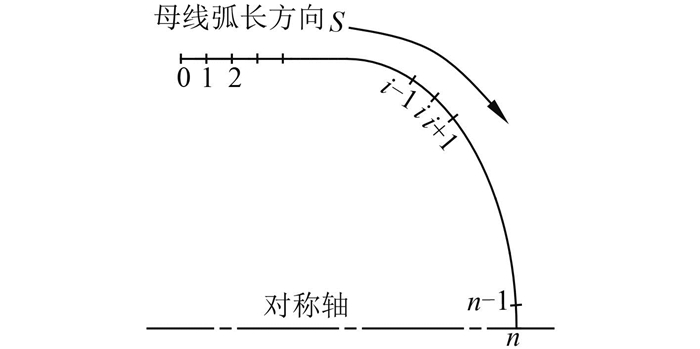
对球面舱壁结构沿母线弧长方向进行离散（见图 3），采用基于两点高斯积分的隐式Runge-Kutta方法推导得到状态向量满足的递推关系式^[5]：

$ {\boldsymbol{U}_{i + 1}} = {\boldsymbol{W}_{i + 1}} \cdot {\boldsymbol{U}_i} + {\boldsymbol{P}_{i + 1}},$

(3)

式中：$\boldsymbol{W}$为场传递矩阵；$\boldsymbol P$为载荷向量。

对于结构不连续（锥壳两端连接斜率突变和肋骨位置）的节点，需要根据力和位移的连续协调条件，建立该节点左右截面状态向量之间的传递关系^[3]：

$\{ \boldsymbol{U}\} _i^R = {\boldsymbol{W}_D}_i \cdot U_i^L,$

(4)

式中：${\boldsymbol{W}_{D}}$为结构不连续处节点的点传递矩阵。

根据起始边界条件将状态向量$\boldsymbol U$分解成状态分向量$\boldsymbol e$和$\boldsymbol f$，分别对应起始边界未知分量和已知分量，采用Riccati变换，即有

${{\boldsymbol f}_{i}}={\boldsymbol{S}_{i}}\cdot {{\boldsymbol e}_{i}}+{\boldsymbol{P}_{i}}{，}$

(5)

按$\boldsymbol f$和$\boldsymbol e$对式（3）矩阵关系进行重排并结合式（5）可得如下关系：

${{\boldsymbol f}_{i+1}}={\boldsymbol{S}_{i+1}}\cdot {{\boldsymbol e}_{i+1}}+{\boldsymbol{P}_{i+1}}{，}$

(6)

${{\boldsymbol e}_{i}}={\boldsymbol{T}_{i}}\cdot {{\boldsymbol e}_{i+1}}+{\boldsymbol{Q}_{i}}{。}$

(7)

其中S，P，T和Q称为Riccati变化矩阵，上述两式分别建立了$\boldsymbol f$和$\boldsymbol e$、i和i+1节点之间状态分量$\boldsymbol e$的关系。

环肋柱壳端部采用固支约束，对应于起始端奇次边界条件，有${\boldsymbol{S}_{0}}=0$和${\boldsymbol{P}_{0}}=0$，由式（5）~式（7）得到各节点$\boldsymbol f$和$\boldsymbol e$满足的矩阵关系；对于末端球壳极点，由于结构形式和载荷的对称性，不难分析得出$u=0$、${{\gamma }_{1}}=0$、${{M}_{1}}=0$或${{N}_{1}}=0$，结合此边界条件即可求解。

本文采用的基于高斯积分的隐式Runge-Kutta数值方法，能有效解决球壳极点处矩阵病态奇异的问题^[5]；Riccati变换使得迭代矩阵的阶数减半，运算量大幅缩减。上述方法的运用保证了传递矩阵法用于球面舱壁结构应力分析计算必要的稳定性和精度。

2 两种舱壁结构强度分析

基于上述Riccati传递矩阵法原理，借助Matlab编制应力计算程序，能直接得到沿舱壁母线上各节点的应力和内力状态量，便于参数化分析。下文将利用应力程序对锥壳过渡、圆环过渡2种球面舱壁进行结构计算，考察过渡环及球壳部分的应力强度。

2.1 锥壳过渡球面舱壁

锥壳过渡球面舱壁结构形式如图 1(a)所示，可以看作球-锥-柱组合旋转壳结构。计算中取球壳半径R=1 340 mm，柱壳半径R₀=1 100 mm，球面舱壁长度H=650 mm，锥壳过渡环长度H₁=221 mm，由几何关系得出半锥角α₁=20.5°和球-锥折角α₂=18.4°，舱壁厚度t=15 mm，过渡锥壳厚度t₁=25 mm，锥壳采用厚板削斜分别与环肋柱壳和球壳连接，A为柱-锥连接点，B为球-锥连接点。

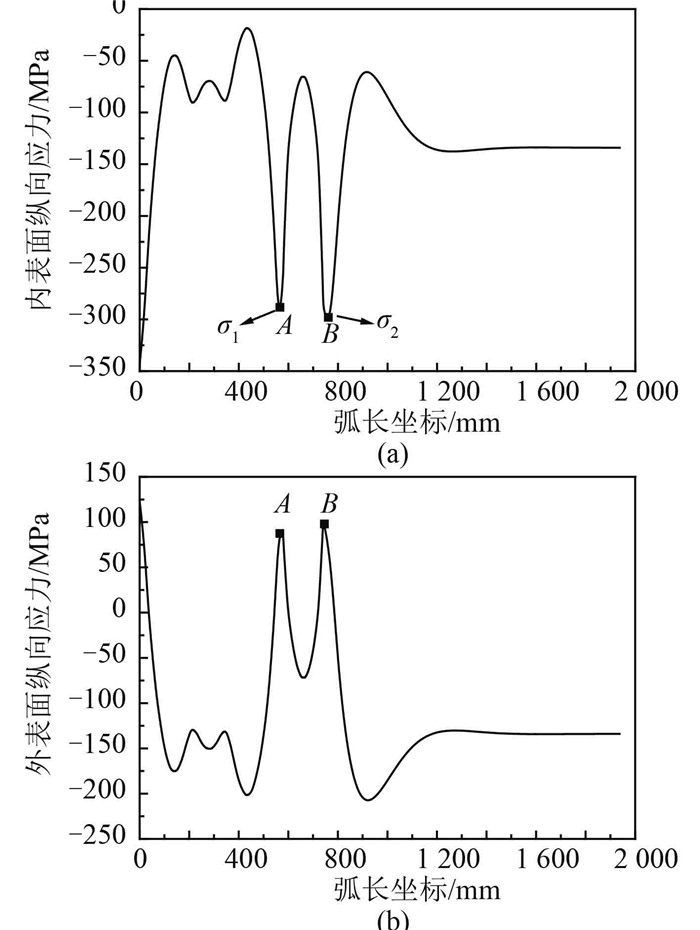
锥壳过渡球面舱壁在均匀外压作用下，有如下应力特征：在柱-锥及球-锥连接处，由于存在高水平的纵向（母线方向）弯矩，内表面纵向应力取得较大峰值σ₁和σ₂（见图 4（a）），显著大于其他应力分量；邻近球-锥连接处的球壳区域在反向弯矩作用下，外表面纵向应力较大（见图 4（b））；环向应力分量幅值相对较小；在球壳部分存在较大的薄膜应力状态区域。

过渡锥壳两端连接处A和B点，由于存在斜率突变出现应力集中现象，应将此两处的内表面纵向应力作为应力校核重点。为了更好地控制锥壳过渡球面舱壁的应力值水平，下文将分析连接处半锥角α₁和球-锥折角α₂对A、B两点内表面纵向应力σ₁和σ₂的影响。

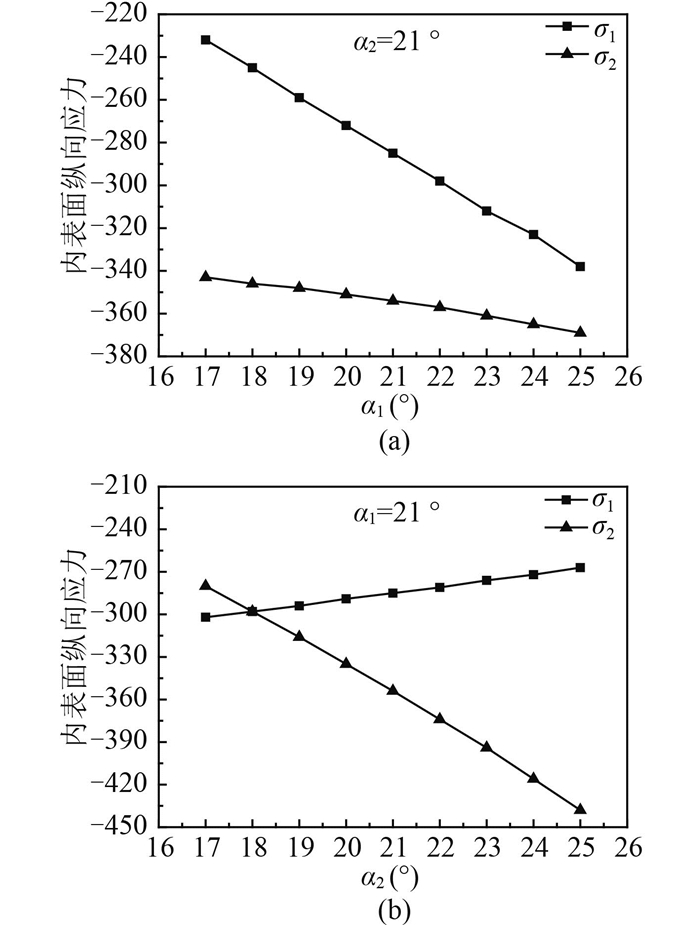
保持锥壳长度H₁不变，分别改变α₁和α₂的值，分析其对σ₁和σ₂的影响。如图 5所示，分别保持α₂=21°和α₁=21°不变。σ₁和σ₂均随α₁和α₂基本呈线性变化；随α₁增大，σ₁和σ₂（幅值，下同）均随之增大，σ₁增大更为显著；随α₁增大，σ₂显著增大，但σ₁却随之减小。在一般情况下，σ₁小于σ₂，α₂对σ₂影响较为显著，因此应优先考虑α₂。

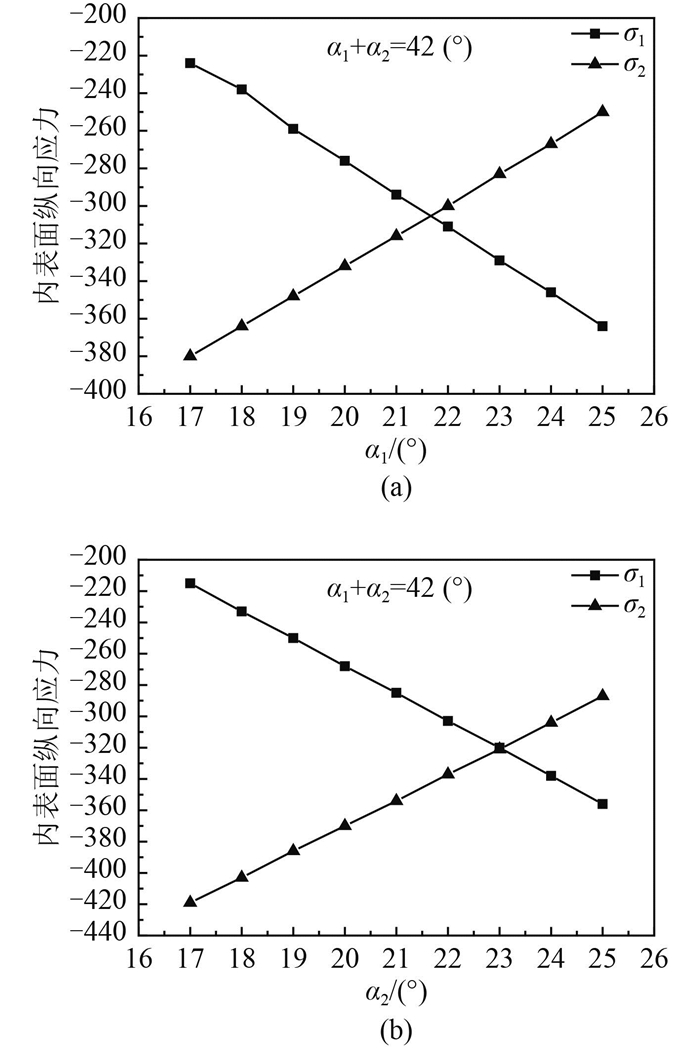
当α₁和α₂越小时，球壳半径R越小，球面舱壁长度H越大，此时σ₁和σ₂均越小，但是H由于其它因素约束一般被限定。在H一定时，如何选取α₁和α₂使得σ₁和σ₂均较小，在锥壳过渡段长度H₁变化不大的条件下，α₁+α₂为定值时，球面舱壁长度H和球壳半径R变化均较小，可近似为保持不变。分别取α₁+α₂=40°和α₁+α₂=42°进行分析，如图 6所示。当α₁稍大于α₂时，σ₁=σ₂取得应力最小值。因此，在H限定条件下，取较小折角α₂（α₂也不宜过小）时，能使得应力水平较低。

2.2 圆环过渡球面舱壁

圆环过渡球面舱壁结构形式如图 1(b)。取球壳半径R=1 340 mm，过渡环半径r=340 mm，柱壳半径R₀=1 100 mm，舱壁厚度t=15 mm，由几何关系可得球面舱壁长度H=690 mm和锥壳过渡环长度H₁=221 mm，圆弧环壳两端分别与环肋柱壳和球壳光滑连接，A为柱-环连接点，B为球-环连接点。

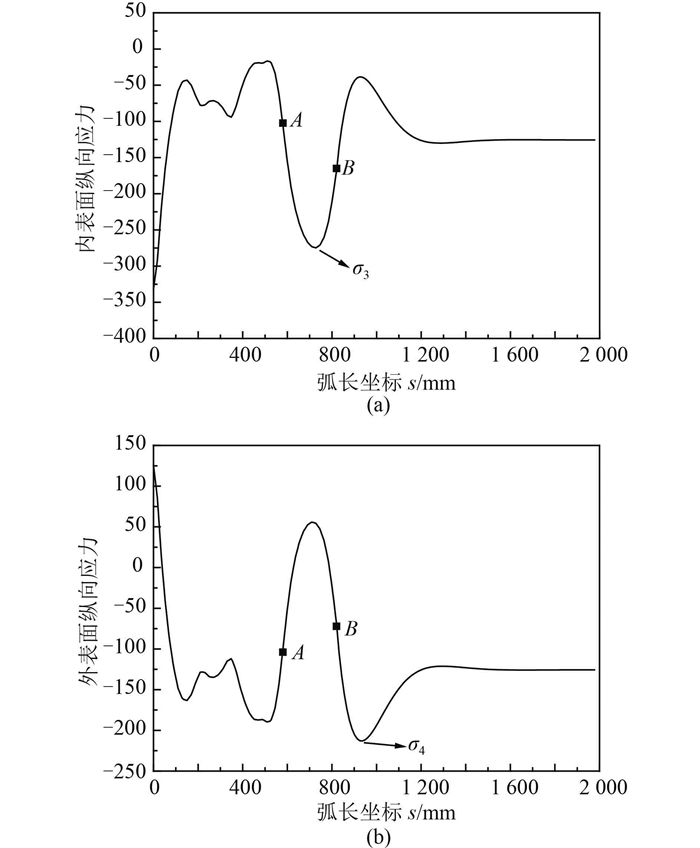
如图 7所示，与锥壳过渡球面舱壁不同的是，内表面最大纵向压应力σ₃出现在过渡环中间区域，而连接点A和B处由于光顺过渡应力水平较低；与壳过渡球面舱壁类似，邻近球-环连接处的球壳区域外表面纵向应力σ₄较大，球壳部分较大区域处于薄膜应力状态。

圆弧过渡球面舱壁中，R尽量取小，r取大时，对应的H也越大，整体应力水平较低^[2]。然而在H一定的条件下，又该如何选取r或R（此时R与r之间存在几何关系），为与柱壳过渡球面舱壁保持一致，取H=650 mm为例，取不同r进行计算，如表 1所示。当r过小时，由于圆环段过短，过渡急促，使σ₃较大；但r过大时，R也较大，舱壁过于扁平，纵向弯矩及其分布范围越大，使σ₄显著增大，σ₃反而增大。因此，对于一定的H，存在特定r或R使得应力状态最佳。本算例中大致取r=413 mm，R=1 527 mm时，应力水平最低。

2.3 两种球面舱壁应力特征对比

为了研究2种球面舱壁结构应力特征的差异，应尽量保持两者结构参数一致，取柱壳半径R₀=1 100 mm，球面舱壁长度H=650 mm，球壳半径R=1 440 mm，舱壁厚度t=15 mm，并保持锥壳和圆环过渡环长度H₁相同。

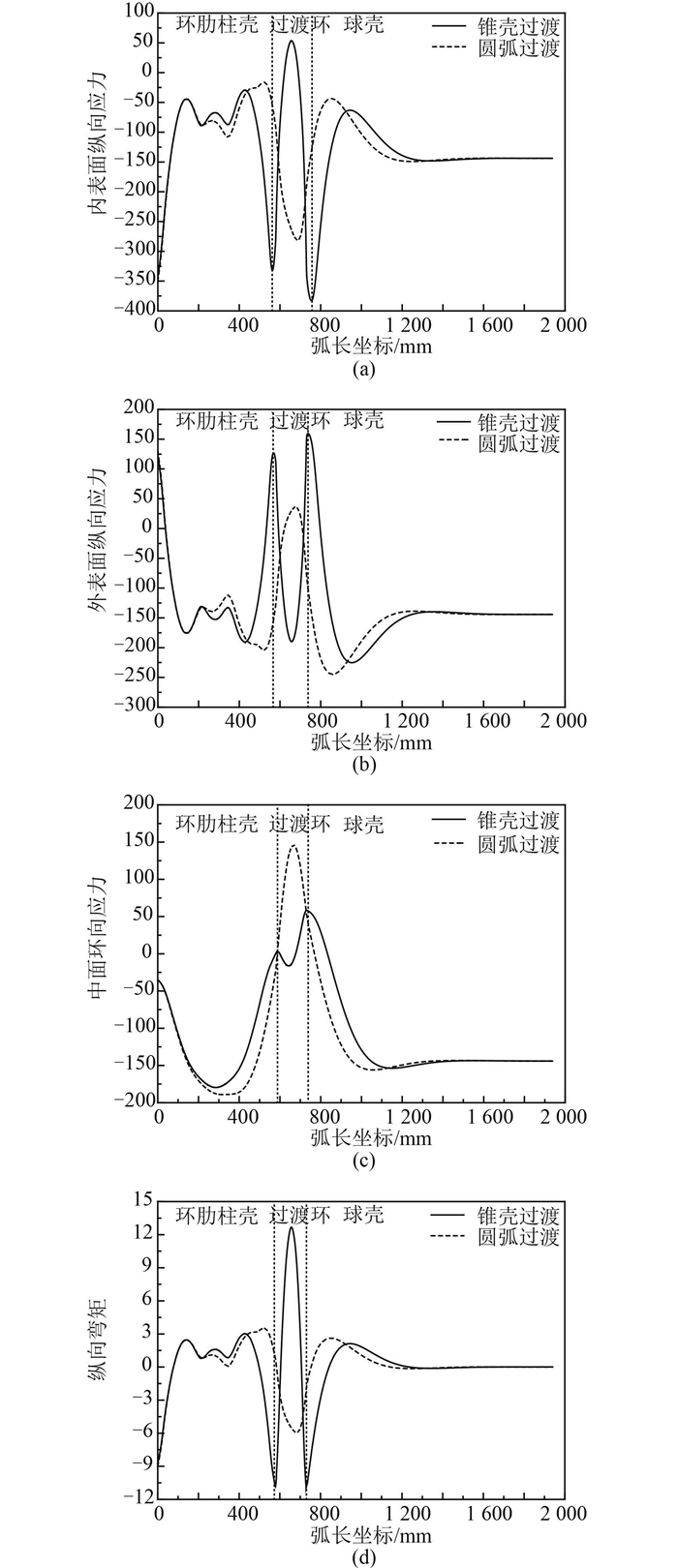
如图 8所示，锥壳过渡形式球面舱壁在A、B两点及过渡环中点存在高水平的纵向弯矩值（图 8（d）弯矩为单位长度的弯矩），使过渡环区域应力分布变化剧烈，A、B点内表面纵向应力峰值σ₁和σ₂较大，容易产生结构疲劳问题；圆环过渡球面舱壁由于过渡环的光顺连接，消除了应力集中现象，但由于过渡环两端还存在曲率突变，在过渡环中间区域和靠近球-环连接处的球壳区域出现了较大纵向弯矩，使得该区域内表面纵向应力值σ₃较大；锥壳过渡球面舱壁的中面环向应力幅值反而较圆弧过渡的低。一般而言，圆弧过渡球面舱壁强度性能更优越。

表 2中，当H₁取值较小时，圆弧过渡球面舱壁中σ₃较大，其应力性能反而不如锥壳过渡球面舱壁；当H₁增大时，σ₃显著减小，球面舱壁应力水平更佳。因此在应用球面舱壁结构时，需要合理选取结构参数，才能体现出圆弧过渡球面舱壁强度性能的优越性。锥壳过渡环球面舱壁虽然力学性能相对较差，但厚板削斜过渡连接已在工程上具有广泛应用，施工工艺成熟；圆环壳为双曲率壳体，高精度成型加工困难，与相邻结构装配精度要求高。

3 结语

本文利用Riccati传递矩阵法对锥壳过渡和圆弧过渡两种球面舱壁结构强度进行了分析。分析表明：锥壳过渡球面舱壁在过渡环两端连接处存在应力峰值，球-环折角α₂较半锥角α₁对应力峰值影响更为敏感，应优先取较小的α₂；对于圆弧过渡球面舱壁，当舱壁长度H一定时，环壳半径r不宜过大也不宜过小，即存在特定的r和球壳半径R，使得应力水平最低；圆弧过渡球面舱壁结构强度性能较锥壳过渡球面舱壁更好，但其工艺要求较高。