0 引言

圆柱壳在工程中得到广泛应用，如船舶、航空、化工和汽车等行业都有圆柱壳的大量实例。圆柱壳的自由振动问题更是得到了持续广泛的研究^[1]。很多学者对于圆柱壳在各种边界条件下的振动问题进行了讨论^[2-5]。除了薄膜简支边界能够得到封闭解外，其他边界的求解往往是采用数值方法获得。对于任意边界问题，系统频率求解都能够转化为一个8阶系数矩阵行列式等于0的问题。

任意边界情况下圆柱壳的自由振动频率求解领域还出现了波传播方法^{[6, 7]}。该方法的主要思路是用梁横向弯曲振动对应的波数代替了圆柱壳的轴向波数，然后代入系统3阶的控制方程进行频率求解。因此它实际上是一种近似方法。

本文采用Flügge薄壳理论^[8]研究任意边界下圆柱壳的振动问题，基于奇异值分解的方法，把行列式的求解问题转化为奇异值求解问题。根据矩阵奇异值的特点，如果系数矩阵的最小奇异值为0，则系数矩阵的行列式也就等于0，从而获得圆柱壳的振动频率。并且，在系统的频散特性曲线上，给出了对应边界条件下的特征频率对应点。本文还和针对任意边界中常用的波传播方法进行比较。对于频散曲线上纯虚数波分支的意义进行探讨。

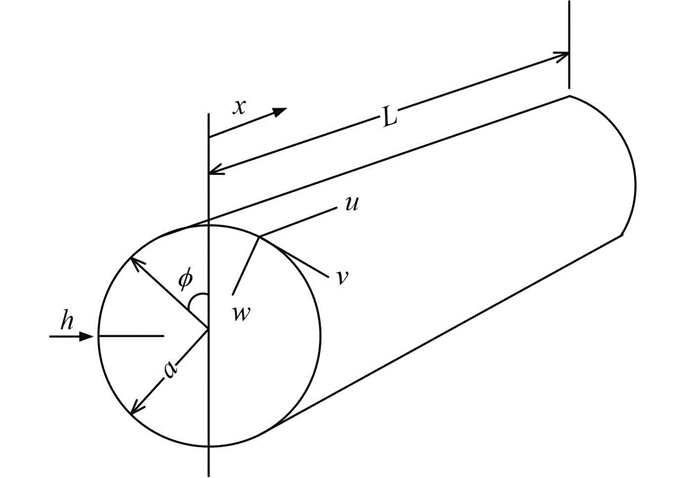
1 理论分析

各向同性材料圆柱壳模型如图 1所示。壳体长度L，中面半径R，厚度h。材料的弹性模量E，泊松比v，剪切模量G，密度ρ。壳体中面在坐标轴（x，φ，z）上位移分量分别为u，v和w（向内为正）。

1.1 圆柱壳控制方程

基于Flugge弹性薄壳理论^[8]，圆柱壳的自由振动方程可表示为：

$ \begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} \begin{array}{l} \displaystyle\frac{{{\partial ^2}u}}{{\partial {x^2}}}+\left({1+k} \right)\displaystyle\frac{{1 - v}}{2}\displaystyle\frac{{{\partial ^2}u}}{{{R^2}\partial {\phi ^2}}}+\frac{{1+v}}{2}\displaystyle\frac{{{\partial ^2}v}}{{R\partial x\partial \phi }} - v\displaystyle\frac{{\partial w}}{{R\partial x}}+\\[10pt] \end{array}\\ \begin{array}{l} \quad \quad \, \, \, \, \, kR\displaystyle\frac{{{\partial ^2}w}}{{\partial {x^3}}} - k\displaystyle\frac{{1 - v}}{2}\displaystyle\frac{{{\partial ^3}w}}{{R\partial x\partial {\phi ^2}}}=\displaystyle \frac{{\rho h}}{D}\displaystyle\frac{{{\partial ^2}u}}{{\partial {t^2}}}{，}\\[10pt] \end{array} \end{array}}\\ {\begin{array}{*{20}{l}} \begin{array}{l} \displaystyle\frac{{1+v}}{2}\displaystyle\frac{{{\partial ^2}v}}{{R\partial x\partial \phi }}+\frac{{{\partial ^2}v}}{{{R^2}\partial {\phi ^2}}}+\left({1+3k} \right)\frac{{1 - v}}{2}\displaystyle\frac{{{\partial ^2}v}}{{\partial {x^2}}} - \\[10pt] \end{array}\\[5pt] {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} \begin{array}{l} \quad \quad \quad \quad \, \, \, \, \, \, \, \displaystyle\frac{{\partial w}}{{{R^2}\partial \phi }}+k\displaystyle\frac{{3 - v}}{2}\displaystyle\frac{{{\partial ^3}w}}{{R\partial {x^2}\partial \phi }}=\displaystyle\frac{{\rho h}}{D}\displaystyle\frac{{{\partial ^2}v}}{{\partial {t^2}}}{，}\\[10pt] \end{array}\\[5pt] \begin{array}{l} v\displaystyle\frac{{\partial u}}{{R\partial x}}+k\displaystyle\frac{{1 - v}}{2}\displaystyle\frac{{{\partial ^3}u}}{{R\partial x\partial {\phi ^2}}} - Rk\displaystyle\frac{{{\partial ^3}u}}{{\partial {x^3}}}+\displaystyle\frac{{\partial v}}{{{R^2}\partial \phi }} - \\[10pt] \end{array} \end{array}}\\ \begin{array}{l} \displaystyle\frac{{3 - v}}{2}k\displaystyle\frac{{{\partial ^3}v}}{{\partial {x^2}\partial \phi }} - {R^2}k\displaystyle\frac{{{\partial ^4}w}}{{\partial {x^4}}} - 2k\displaystyle\frac{{{\partial ^4}w}}{{\partial {x^2}\partial {\phi ^2}}} - \\[10pt] \end{array} \end{array}}\\[5pt] {\begin{array}{*{20}{l}} {k\displaystyle\frac{{{\partial ^4}w}}{{{R^2}\partial {\phi ^4}}} - 2k\displaystyle\frac{{{\partial ^2}w}}{{{R^2}\partial {\phi ^2}}} - \left({1+k} \right)\displaystyle\frac{w}{{{R^2}}}=\displaystyle\frac{{\rho h}}{D}\displaystyle\frac{{{\partial ^2}w}}{{\partial {t^2}}}}{。}\\ \end{array}} \end{array}} \end{array} $

(1)

其中：t为时间；$D=\displaystyle\frac{{Eh}}{{1 - {v^2}}}$；$k=\displaystyle\frac{{{h^2}}}{{12{R^2}}}$。

对于任意边界条件，假设壳体中面位移可表示为：

$ \begin{array}{l} u\left({x, \phi, t} \right)={U_0}{e^{\lambda x}}\cos \left({n\phi } \right)\cos \left({\omega t} \right){，}\\ v\left({x, \phi, t} \right)={V_0}{e^{\lambda x}}\cos \left({n\phi } \right)\cos \left({\omega t} \right){，}\\ w\left({x, \phi, t} \right)={W_0}{e^{\lambda x}}\cos \left({n\phi } \right)\cos \left({\omega t} \right){。} \end{array} $

(2)

式中：U₀，V₀和W₀为振幅；λ为轴向波数；n为周向波数；ω为振动圆频率（1/s）。将式（2）代入式（1），可得到如下矩阵形式的控制方程：

$ \left[{\begin{array}{*{20}{c}} {{C_{11}}} &{{C_{12}}} &{{C_{13}}}\\ {{C_{21}}} &{{C_{22}}} &{{C_{23}}}\\ {{C_{31}}} &{{C_{32}}} &{{C_{33}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{U_0}}\\ {{V_0}}\\ {{W_0}} \end{array}} \right\}=\left\{ {\begin{array}{*{20}{c}} 0\\ 0\\ 0 \end{array}} \right\}{。} $

(3)

系数矩阵$C=\left[{{C_{ij}}} \right]\left({i, j=1, 2, 3} \right)$的元素如下：

$ \begin{array}{l} {C_{11}}={R^2}{\lambda ^2}+\frac{1}{2}\left({1+k} \right){n^2}\left({ - 1+\nu } \right)+{\Omega ^2}, \\ {C_{12}}=\frac{1}{2}nR\lambda \left({1+\nu } \right), \\ {C_{13}}=k\left({{R^3}{\lambda ^3}+\frac{1}{2}{n^2}R\lambda \left({1 - \nu } \right)} \right)- R\lambda \nu, \\ {C_{21}}=- \frac{1}{2}nR\lambda \left({1+\nu } \right), \\ {C_{21}}=- \frac{1}{2}nR\lambda \left({1+\nu } \right), \\ {C_{22}}=\frac{1}{2}\left({ - 2{n^2} - \left({1+3k} \right){R^2}{\lambda ^2}\left({ - 1+\nu } \right)+2{\Omega ^2}} \right), \\ {C_{23}}=n+\frac{1}{2}kn{R^2}{\lambda ^2}\left({ - 3+\nu } \right), \\ {C_{31}}=k\left({ - {R^3}{\lambda ^3} - \frac{1}{2}{n^2}R\lambda \left({1 - \nu } \right)} \right)+R\lambda \nu, \\ {C_{31}}=k(- {R^3}{\lambda ^3} - \frac{1}{2}{n^2}R\lambda(1 - v))+R\lambda v, \\ {C_{32}}=n+\frac{1}{2}kn{R^2}{\lambda ^2}\left({ - 3+\nu } \right), \\ {C_{33}}=- 1 - k\left({1+{n^4}+{R^4}{\lambda ^4} - 2{n^2}\left({1+{R^2}{\lambda ^2}} \right)} \right)+{\Omega ^2}. \end{array} $

方程（3）存在非零解的条件是系数行列式等于0，即

$ \det \left({\left[C \right]} \right)=0{。} $

(4)

式（4）即为圆柱壳自由振动的控制方程。该方程是关于圆柱壳几何参数以及材料参数的特征方程，该方程展开之后，可改成为关于轴向波数λ的8次方程或者频率ω的6次代数方程，即

$ {g_8}{\lambda ^8}+{g_6}{\lambda ^6}+{g_4}{\lambda ^4}+{g_2}{\lambda ^2}+{g_0}=0{，} $

(5)

或者

$ {b_6}{\omega ^6}+{b_4}{\omega ^4}+{b_2}{\omega ^2}+{b_0}=0{。} $

(6)

设定圆柱壳的几何参数和材料参数，并假设环向振动波数n之后，对于方程（4）而言，未知数就是轴向波数λ和频率ω。

对于圆柱壳而言，端部（x=0，L）的边界条件包括位移和转角约束以及力、力矩约束，即

$ \begin{array}{l} u=0, \;v=0, \;w=0, \;\displaystyle\frac{{\partial w}}{{\partial x}}=0{，}\\[5pt] {N_x}=0, \;{R_x}=0, \;{S_x}=0, \;{M_x}=0{。} \end{array} $

(7)

其中：${R_x}={N_{x\theta }} -\displaystyle\frac{1}{R}{M_{x\theta }}$，为Kirchhoff薄膜力；${S_x}={Q_x}+\frac{1}{R}\displaystyle\frac{{\partial {M_{x\theta }}}}{{\partial \theta }}$，为Kirchhoff薄膜剪力。把位移表达式（2）代入边界条件（7），就能够得到未知数轴向波数λ和频率ω的边界控制方程。

联立边界控制方程（7）及方程（4）就能够求解任意边界下圆柱壳的振动频率以及对应的轴向波数、环向波数。依据（5）式，对于自由振动问题，方程的根可写成

$ \lambda=\pm {\lambda _1}, \;\pm i{\lambda _2}\;\pm \left({{\lambda _3} \pm i{\lambda _4}} \right){，} $

(8)

其中λ₁，λ₂，λ₃，λ₄都是正的实数。对于这8个根，再分别求出振型。

$ \alpha=\frac{{{U_0}}}{{{W_0}}}，beta=\frac{{{V_0}}}{{{W_0}}}{。} $

(9)

位移函数式（2）可改写成为

$ \begin{array}{l} u\left[{x, \phi, t} \right]=\sum\limits_{i=1}^8 {{\alpha _i}{W_i}{e^{{\lambda _i}x}}\cos \left({n\phi } \right)\cos \left({\omega t} \right)} {，}\\ v\left[{x, \phi, t} \right]=\sum\limits_{i=1}^8 {{\beta _i}{W_i}{e^{{\lambda _i}x}}\cos \left({n\phi } \right)\cos \left({\omega t} \right)}{，} \\ w\left[{x, \phi, t} \right]=\sum\limits_{i=1}^8 {{W_i}{e^{{\lambda _i}x}}\cos \left({n\phi } \right)\cos \left({\omega t} \right)} {。} \end{array} $

(10)

代入边界条件（7），可以得到一个关于W_i的8阶齐次方程组

$ { \boldsymbol A _{8 \times 8}}\left\{ W \right\}=\left\{ 0 \right\}{，} $

(11)

其中：${\boldsymbol W}={\left\{ {{W_1}, {W_2} \ldots {W_8}} \right\}^{\rm T}}$为8×1的列向量。式（11）含1个未知量即圆柱壳的振动频率ω。令系数矩阵A的行列式等于0：

$ \det(A)=0{。} $

(12)

可以求得频率ω。式（12）是一个关于频率的超越方程。注意，A是一个复数矩阵。

1.2 基于SVD技术的特征方程求解

同时满足式（4）和式（12）的频率就是圆柱壳的自由振动特征频率。对于不包括边界条件的式（5）或者式（6），波数λ（或频率ω）可以用频率（或者波数）精确表达。对于上述求解过程，边界条件方程（12），很难给出频率封闭解的形式。通常采用“扫频”的数值算法进行求解。即设定一定的频率范围，依照一定的频率步长进行扫频计算。这个方法涉及到8阶矩阵行列式的计算问题。大量的算例表明，在一定的几何参数和振型状态下这个系数矩阵会变成病态矩阵^[9]，即矩阵的条件数很大。矩阵元素细微的改变，都会引起行列式剧烈的改变，计算的难度也相应增大。

本文拟采用奇异值分解技术进行探讨。假定A是M×N的矩阵，可以将A矩阵分解为^[10]

$ A=U\sum {{V^{\rm T}}}{。} $

(13)

其中：${\boldsymbol U_{M \times M}}$和${\boldsymbol V_{N \times N}}$为列向量正交的单位矩阵，即U和V分别满足$\boldsymbol U \times {\boldsymbol U^{\rm T}}=I$，$V \times {V^{\rm T}}={\boldsymbol I}$；I为单位矩阵，分别称为A矩阵的左、右奇异向量；∑为M× N的对角矩阵；$S=diag\left({{s_1}, {s_2}, \ldots {s_p}} \right)$；并且满足${s_1} \geqslant {s_2} \geqslant \ldots \geqslant {s_p} \geqslant 0$；p为矩阵A的奇异值。根据行列式的性质，

$ \begin{aligned} \det \left(\boldsymbol A \right)&=\det \left({U\sum {{V^{\rm T}}} } \right)=\det \left(U \right)\det \left(\Sigma \right)\det \left({{V^{\rm T}}} \right)=\\ &\left({ \pm 1} \right)\det \left(\Sigma \right)=\left({ \pm 1} \right){s_1} \times {s_2} \times \ldots \times {s_p}{。} \end{aligned} $

(14)

注意，$\det \left(U \right)=\pm 1, \;\det \left({{V^T}} \right)=\pm 1$，式（14）说明，A矩阵的行列式是它的奇异值的乘积（带正负符号）。当A矩阵的最小奇异值为0，A矩阵的系数行列式也为0。于是对（12）式零点的寻找，就转换为求解那些使得A矩阵最小奇异值为0的频率点。

对于本文讨论的式（12），A矩阵在扫频过程中，仅仅是在频率点处，最小奇异值为0，其秩变7。其余的频率点上A是满秩矩阵，共有8个奇异值。

在实际计算过程中，频率点处最小奇异值并不精确等于零。如果最小奇异值很小，或者利用矩阵条件数极值判断，最小奇异值相对其他7个奇异值非常小，则该最小奇异值可以近似认为是0，也就是可以认为det（A）=0，即找到频率点。

在奇异值求解过程中，还存在前1~2阶极小值点的判断问题情况。本文结合方程（4）给出频散曲线，此图能够很好解决该问题。

2 数值算例和讨论

基于Matlab平台，采用奇异值分解技术讨论了圆柱壳在任意边界条件下的自由振动计算问题。本文首先计算1个两端薄膜简（SD-SD）圆柱壳的算例。基本参数是：L=0.4 m，h=0.004 m，R=0.1 m，E=2.1×10¹¹ N/m²，v=0.3，即

$ v=0, \;w=0, \;{N_x}=0, \;{M_x}=0, \;x=0{，} $

(15)

引入频率无因次表达式

$ {\Omega ^2}=\frac{{\rho {R^2}\left({1 - {v^2}} \right)}}{E}{\omega ^2}{。} $

(16)

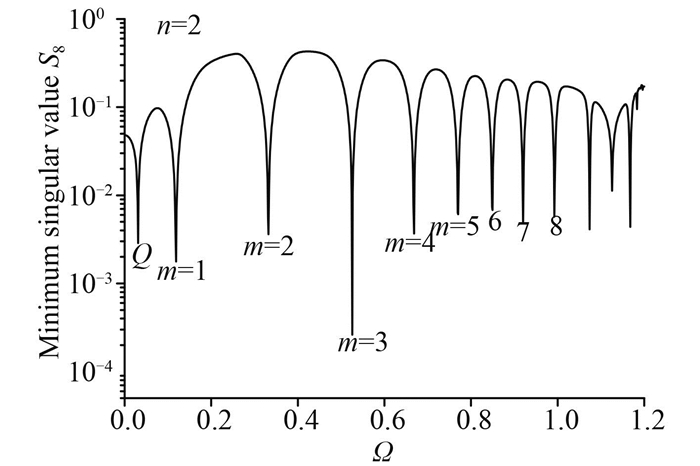
图 2给出了n=2时最低奇异值s₈随频率Ω变化的曲线图。从图中可看出，由于数值误差，最小奇异值并不严格等于0，曲线出现了连续的局部极小值。

分析这些局部极小值点频率以及它们对应的8个波数λ，通过径向位移${e^{{\lambda _2}x}}$（即λ的纯虚根，见方程（8））的虚部值沿x的方向判断壳体的轴向振型。这些尖点对应着轴向振型半波数m=1，2，…。图 3给出了前3阶轴向振型，标注了这3阶振型对应λ的纯虚数根。前8阶的频率对应值分别为0.118 8，0.332 4，0.525 6，0.668 4，0.769 2，0.848 4，0.920 4和0.992 4。

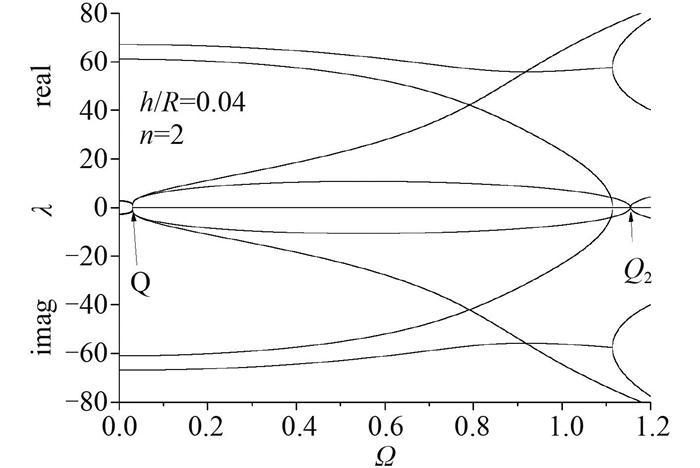
注意到图 2中Q点，它也是最小奇异值曲线的第一个局部极小值点，对应频率Ω_Q=0.031 0。对于该点是否为自振频率的判断还需要借助方程（4）。方程（4）是关于波数λ和频率Ω的方程，实际上就是圆柱壳的频散方程（见图 4）。在图 4中，Q点其实是第1支传播波的起始频率^[11]。当外界激励频率小于Ω_Q时，圆柱壳内的波均为耗散波，此时对应的波数λ是8个复数，并没有纯虚根出现。当激励频率大于Ω_Q，圆柱壳内才产生第1支传播波。起始频率也是波数λ=0对应的频率。在（6）式中令λ=0可以求解出3个起始频率分别为（0.031 0，1.183 2，2.236）。第2支传播波的起始频率用Q₂（Ω_Q2=1.183 2）点标注在图 4中。

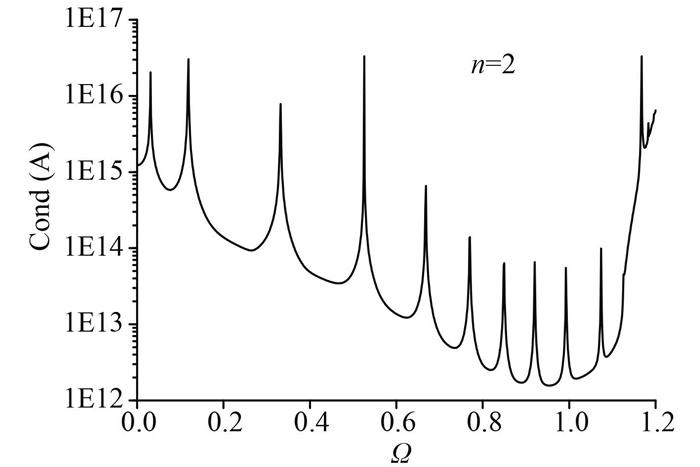
条件数是判断矩阵是否为病态的重要参数，同时也能够作为频率和轴向振型的判断依据。图 5给出了系数矩阵A的条件数随频率变化的情况。从图中看出，条件数的变化范围在10¹²~10¹⁷之间。根据矩阵理论，如果A矩阵非奇异，其条件数的定义为^[10]：

$ cond\left(\boldsymbol A \right)=\left\| \boldsymbol A \right\| \cdot \left\| {{\boldsymbol A^{ - 1}}} \right\|{，} $

(17)

其中$\left\| A \right\|$为矩阵的范数。注意，条件数也是最大奇异值和最小奇异值的比值^[10]，即

$ cond\left(A \right)=\frac{{{s_{\max }}}}{{{s_{\min }}}}=\frac{{{s_1}}}{{{s_8}}}{。} $

(18)

根据矩阵奇异值分解的特点，奇异值具有稳定性特点，当矩阵受到微小的扰动其变化并不明显。在自由振动的频率处，根据式（12）此时A矩阵恰好是奇异的。表现在图 5中，这些频率对应的条件数是其局部极大值。

对于奇异值分解的精度判断依据，可以根据式（13）计算残差

$ \Delta={\left\| {U\sum {{V^{\rm T}}} - A} \right\|_2}{。} $

(19)

其中下标2为矩阵的2-范数。

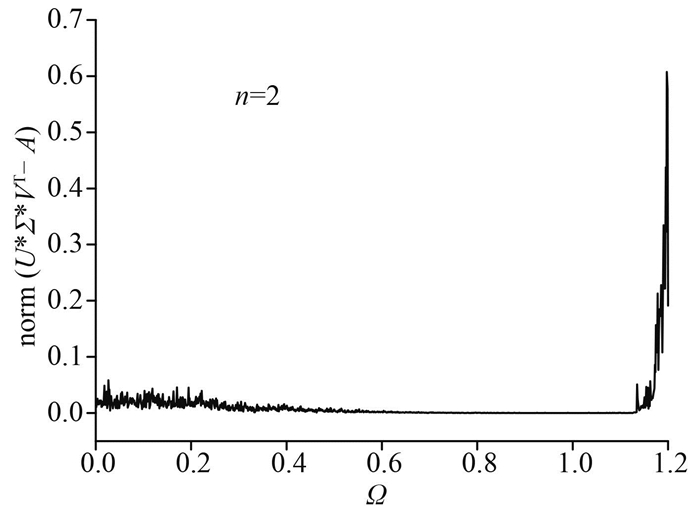
图 6给出了残差的变化情况。从图 6可以看出，奇异值分解的精度可信。

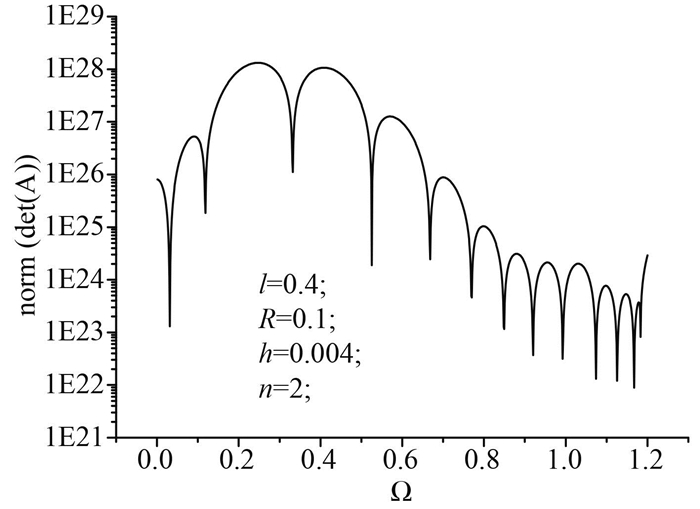
在Matlab平台中，矩阵行列式的求解是基于LU分解的^[12]。在条件数很大的情况下，系数矩阵行列式的计算就可能导致不准确，图 7给出了系数矩阵A行列式的变化。A是一个复数矩阵，其行列式一般也是复数，图 7给出的是行列式的模。与最小奇异值的变化规律类似，图中也出现了连续的极小值分布情况。经过大量的数值试验发现，对于一些特定的参数组合情况，存在计算残差比较大的情况，就需要联合行列式和最小奇异值图及频散曲线共同判断。

通过变换式（7）的不同组合形式，可以计算其他的边界情况。这里计算了C-C和C-SD两种边界下的频率，并且和其他的算法及实验结果进行了比较（见表 1和表 2）。从表中可看出，使用最小奇异值求解的方法精度良好。

本文给出的是一种精确解法。对于圆柱壳的轴向振动模态表示，除了式（2）中的指数型以外，还采用多项式（1次，2次）等形式。采用多项式可以简单模拟圆柱壳的边界条件，可以简化计算过程。在多项式表达中最简单的是采用梁的振型函数，即把圆柱壳在端部3个方向上的边界用一维梁结构的边界代替，也就是通过设定边界预先得到了轴向波数λ（纯实数）。然后代入圆柱壳控制方程（4）（或者式（6）），可以得到频率的封闭解。这也是波传播法的主要思路。这些的简化是会带来误差的。本文的方法能够作为一个基准，可以校核其他方法的精确度。

圆柱壳的频散曲线是反映无限长圆柱壳受到外界激励频率之后波传递的特性，同时也能够帮助理解壳体的自由振动和边界特性。频散曲线是不包括边界条件的，当边界确定之后，圆柱壳的振动特征参数（频率和对应波数）就分布在这个曲线的某个部分。因此，频散曲线也包括了各种边界条件下圆柱壳自由振动的信息频率。下面讨论不同边界自振频率和频散曲线之间的联系。考虑如下圆柱壳算例：L=0.3 m，R=0.1 m，h=0.005 m，v=0.3，n=5。

以SD-SD边界为例，采用前述方法，得到轴向振型m=1，2，3的频率是0.356 4，0.423 8，和0.546 1。计算这3个频率对应的8个轴向波数中纯虚数解iλ₂分别是：10.429 7i，21.000 7i和31.432 7i。图 8给出了对应的频散图，并标注了SD-SD边界对应的波数值（表达在下半部图形）。

若采用经典简支梁的函数，根据梁弯曲振动的控制方程^[16]：

$ \sin \left({{\lambda _{beam1}}L} \right)=0{，} $

(20)

得到对应的波数λ_beam1=mπ/L=（1，2，3）π/L=10.472，20.944，31.415 9。可见采用梁边界的计算与圆柱壳的精确计算很接近。在频散图形中，纯虚数波那一支曲线上，包括了边界条件对应的频率-波数解。

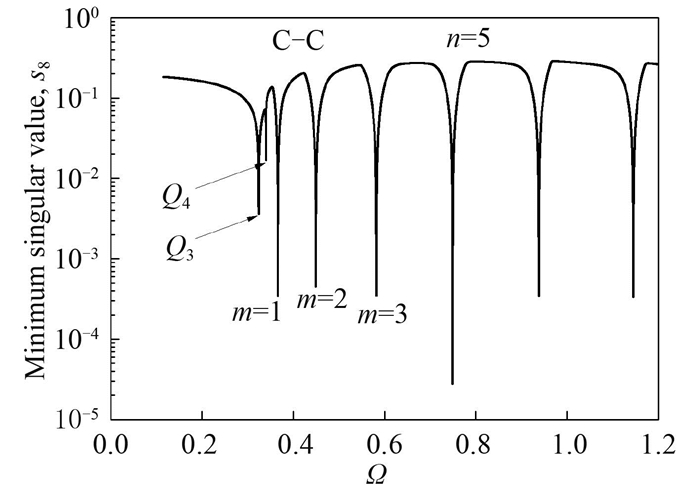
对于其他边界情况，当边界约束加上之后，圆柱壳的自振频率点仍然包括在纯虚数分支曲线上的。假设边界条件为C-C，则轴向m=1，2，3对应的前3个频率是0.366 1，0.449 9和0.581 8，见图 9。图对应的纯虚数波数iλ₂分别是12.759 3i，23.611 8i和33.975 8i。固定支撑边界梁弯曲的特征方程为

$ 1 - \cosh \left({{\lambda _{beam2}}L} \right)\cos \left({{\lambda _{beam2}}L} \right)=0{。} $

(21)

前3阶特征根为λ_beam2=4.730，7.853和10.996，对应的波数则为15.766 6，26.176 6和36.653 3。这也说明，随着约束条件的增强，采用梁的边界条件近似圆柱壳的边界条件引起误差会变大。

从图 9可看到，在第1阶轴向模态之前，最小奇异值曲线还有2个极小值点Ω_Q3=0.324 0和Ω_Q4=0.339 7。经过和频散曲线（见图 8）联合分析可以知道，Q₃和Q₄两点的波数均为0。Q₃对应于8个复数波开始分化为传播波、耗散波。Q₄是起始频率点，它对应于耗散波的一个分支，大于此起始频率后，第1支传播波开始形成。注意到，起始频率也是无限长圆柱壳（即波数为0）时的频率，Rayleigh曾给出无伸长弯曲振动圆柱壳的频率公式^[17]

$ \varOmega _R^2=\frac{{k{n^2}{{\left({{n^2} - 1} \right)}^2}}}{{{n^2}+1}}{。} $

(22)

经过计算Ω_R=0.339 7，和Ω_Q4相等。

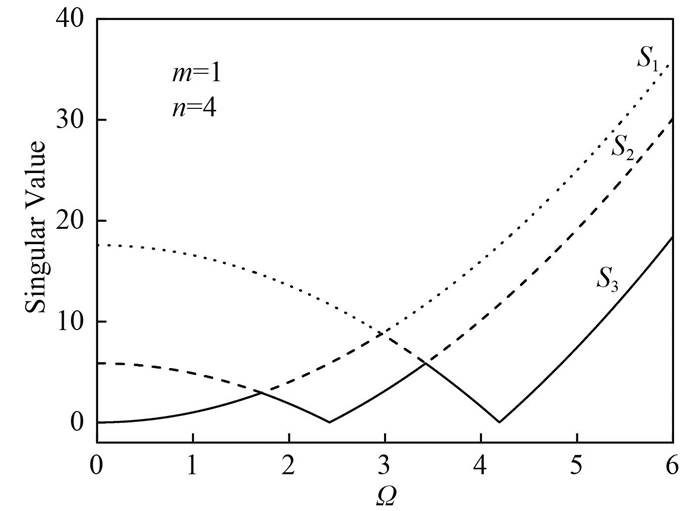
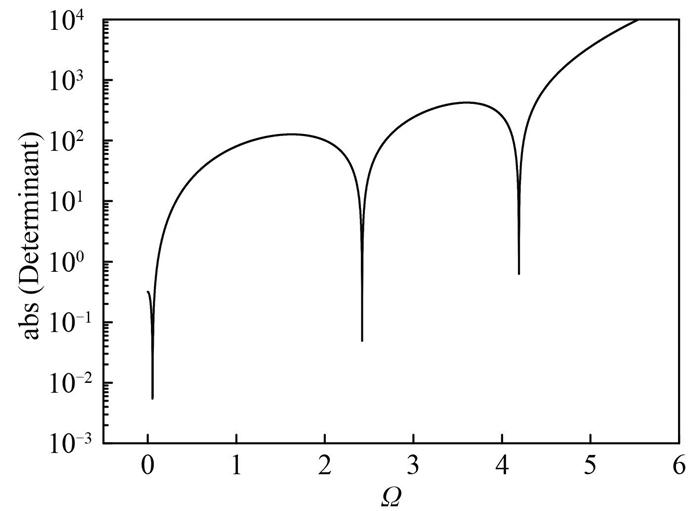
对于圆柱壳的SD-SD边界，有很多研究者使用梁的特征波数λ_beam=m×πL求解圆柱壳的频率。在这种情况下也可以针对3阶矩阵C进行奇异值分解而求解圆柱壳的频率。假设圆柱壳的主要参数R=0.1 m；L=0.4 m；h=0.001 m；m=1；n=4；此时圆柱壳的3个振动频率是0.055 5，2.421 1和4.191 6。这3个频率分别对应径向、轴向和环向为主的振动形式。3个奇异值以及系数矩阵行列式随频率的变化曲线如图 10，11所示。当边界条件用梁的条件给定，此时系数矩阵C的条件数很小，是一个普通的矩阵，通过图 11可以知道，系统行列式的精度很好。

3 结语

本文采用奇异值分解和频散曲线讨论了任意边界条件下圆柱壳的自由振动问题。经过分析可以得出以下结论：

1）最小奇异值曲线的极小值可以给出不同轴向振型时的频率。该曲线最初的1个或者2个频率极小点往往是耗散波的截止频率或者是传播波的起始频率。对于最低自振频率的确定需要结合频散曲线进行分析判断。

2）圆柱壳的轴向振型通过纯虚数波数给出，对于任意边界，其自然频率-波数点对应于频散图中的纯虚数波那条曲线上。

3）基于通常梁横向振动特征波数的波传播法是一种近似的方法，它对于较长的圆柱壳精度良好，但是当圆柱壳比较短，环向波数较大，边界约束越大，则误差也越大。