船舶一般都是从事特种作业,对定位要求很高,因而其定位精度和可靠性尤为重要[1]。对于船舶状态估计器来说,它的主要作用就是滤去测量值的高频噪声,将测量值分为低频和高频两部分,以便将低频信号反馈给控制器。由于根据运动学和动力学建立的船舶运动数学模型非线性,所以船舶状态估计的问题就转化为非线性滤波的问题[2]。
对于线性高斯滤波问题,用卡尔曼滤波方法设计的估计器就可以很好地近似系统真实状态。而我们所研究的船舶模型现实中具有很强的非线性,所以传统的卡尔曼滤波并不适用。
近几十年来,学者们提出各种非线性滤波方法,其中比较有代表性的有扩展卡尔曼滤波(EKF)[3]、无迹卡尔曼滤波(UKF)[4]、容积卡尔曼滤波(CKF)等[5]。这些滤波方法都要求假设噪声服从高斯分布,不具备对测量野值的鲁棒性。当有测量野值出现时,滤波效果变差甚至发散。
以上滤波方法都对适用的系统模型或噪声分布作出了一定的限制[6],直到基于序贯重要性采样的蒙特卡罗模拟思想引入贝叶斯滤波理论(Bayesian Filtering Theory),即粒子滤波的提出,才完全摆脱了滤波方法对于系统状态模型的特性以及噪声分布的限制[7]。粒子滤波基于蒙特卡罗模拟方法实现递推贝叶斯滤波估计,采用加权的随机样本集合近似系统状态的后验概率密度分布,能够有效处理非线性、非高斯系统的状态估计问题;并且由于蒙特卡罗模拟方法以大数定律为基础,因此粒子滤波方法可以方便地扩展到高维情况[8]。从提出之初,到目前历经20余年的发展,粒子滤波的算法和概念逐步完善成一整套理论和框架。当然其中仍然存在一些缺点及不足,如粒子退化现象、样本贫化问题,以及运算量较大、实时性难以保证等问题,为此不同领域的研究者们提出了多种优化改进方法,促进了粒子滤波研究的蓬勃发展。
在建议分布的选择方面,Zaritskii证明最优的重要密度函数为
此外,Arash Mohammadi and Amir Asif提出了一种基于一致性的分布式无迹粒子滤波方法(CD/UPF),扩展了分布式卡尔曼滤波框架,非高斯激励的分布式动力系统。它的主要优点是在推导动力系统中使用所有可利用的局部观测值,包括最近值;从局部估计到全局估计的计算过程中基于最优融合规则,其追踪性能与中心粒子滤波相同[10]。文献[11]提出了一种改进的无迹粒子滤波算法(IUPF)。与传统的粒子滤波算法不同,IUPF中每个粒子并不代表状态序列的一个可能实现,而是代表由初始状态以及过程噪声序列所构成的扩展过程噪声序列的一个可能实现。IUPF可以采用不同的无迹变换方法来设计建议分布,借鉴了基于无迹变换的辅助粒子滤波器(UTAPF)的思想来改进重采样过程,体现了较好的估计能力。文献[12]将无迹粒子滤波应用在AUVs的协同控制上,让无迹卡尔曼滤波作用在粒子滤波算法的每个粒子上,当粒子更新时,让粒子混合到测量值的后验信息中,在一定程度上解决了粒子损耗问题,提高了滤波的有效性。目前,粒子滤波技术已经应用到诸多领域,如目标跟踪及导航制导系统,故障检测,参数估计与系统识别等。但粒子滤波对海洋运动控制方面的应用很少,粒子滤波可以在复杂的海洋状况下进行目标识别定位和环境参数估计,最后可以给出高精度的目标估计和环境参数估计。
本文将主要针对粒子滤波存在的粒子退化现象以及样本贫化问题,进行粒子滤波改进算法的研究;并结合船舶非线性观测器问题的应用,采用一种基于高斯粒子滤波的状态估计器[13],用Unscented卡尔曼滤波求得的高斯分布来近似后验分布,提出一种改进的高斯粒子滤波,此非线性滤波算法不会产生粒子退化问题,省去了重采样的步骤,使算法的计算量降低,复杂度也降低。将改进高斯粒子滤波非线性状态估计器用于船舶动力定位系统,仿真结果验证了其有效性。
1 非线性滤波方法 1.1 序贯重要性采样考虑如下非线性状态空间模型:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\boldsymbol{x}}_k}={f_{k - 1}}({{\boldsymbol{x}}_{k - 1}}, {{\boldsymbol{w}}_{k - 1}})},\\ {{{\boldsymbol{z}}_k}={h_k}({{\boldsymbol{x}}_k}, {{\boldsymbol{v}}_k})}。\end{array}}\right.$ | (1) |
式中:
非线性系统最优滤波方法可由递推贝叶斯滤波描述,递推贝叶斯滤波将系统状态估计问题转化成计算后验概率密度问题,其预测和更新过程如下:
| $ p({{\boldsymbol{x}}_k}|{{\boldsymbol{Z}}^{k - 1}})=\int {p({{\boldsymbol{x}}_k}, {{\boldsymbol{x}}_{k - 1}})p({{\boldsymbol{x}}_{k - 1}}|{{\boldsymbol{Z}}^{k - 1}}){\rm d}{{\boldsymbol{x}}_{k - 1}}},$ | (2) |
| $ p({{\boldsymbol{x}}_k}|{{\boldsymbol{Z}}^k})=\frac{{p({{\boldsymbol{z}}_k}|{{\boldsymbol{x}}_k})p({{\boldsymbol{x}}_k}|{{\boldsymbol{Z}}^{k - 1}})}}{{\int {p({{\boldsymbol{z}}_k}|{{\boldsymbol{x}}_k})} p({{\boldsymbol{x}}_k}|{{\boldsymbol{Z}}^{k - 1}}){ \rm d} {{\boldsymbol{x}}_k}}}。$ | (3) |
其中
| $ \hat p({{\boldsymbol{x}}_k}|{{\boldsymbol{Z}}^k})=\frac{1}{N}\sum\limits_{i=1}^N {\delta({{\boldsymbol{x}}_k} - {\boldsymbol{x}}_k^i)}。$ | (4) |
其中
| $\begin{array}{c} E({{\boldsymbol{x}}_{0:k}})\!=\!\! \int\!\! {{{\boldsymbol{x}}_{0:k}}} \frac{{p({{\boldsymbol{x}}_{0:k}}|{{\boldsymbol{Z}}^k})}}{{q({{\boldsymbol{x}}_{0:k}}|{{\boldsymbol{Z}}^k})}}q({{\boldsymbol{x}}_{0:k}}|{{\boldsymbol{Z}}^k}){\rm d}{{\boldsymbol{x}}_{0:k}} \approx \!\frac{1}{N}\sum\limits_{i=1}^N {\omega _k^i} {\boldsymbol{x}}_{0:k}^i。\!\!\!\!\end{array} $ | (5) |
其中
| $ \omega _k^i=\omega _{k - 1}^i\frac{{p({{\boldsymbol{z}}_k}|{\boldsymbol{x}}_k^i)p({\boldsymbol{x}}_k^i|{\boldsymbol{x}}_{k - 1}^i)}}{{q({\boldsymbol{x}}_k^i|{\boldsymbol{x}}_{k - 1}^i, {{\boldsymbol{Z}}^k})}}。$ | (6) |
对于上述非线性状态空间模型,选取先验概率密度
1)初始化
从
2)序贯重要性采样(SIS)
①重要密度函数:
从重要密度函数中抽取N个预测粒子
②计算粒子权值
| $ \omega _k^i=\omega _{k - 1}^i\frac{{p({{\boldsymbol{z}}_k}|{\boldsymbol{x}}_k^i)p({\boldsymbol{x}}_k^i|{\boldsymbol{x}}_{k - 1}^i)}}{{q({\boldsymbol{x}}_k^i|{\boldsymbol{x}}_{k - 1}^i, {{\boldsymbol{Z}}^k})}};$ | (7) |
③归一化权值
| $ \hat \omega _k^i=\omega _k^i/\sum\limits_{i=1}^N {\omega _k^i}。$ | (8) |
3)重采样
①计算有效粒子容量
| $ {N_{eff}} \approx \frac{1}{{\sum\limits_{i=1}^N {{{(\hat \omega _k^i)}^2}} }};$ | (9) |
②若
4)状态和方差估计
| $ {{\boldsymbol{\hat x}}_k}=\sum\limits_{i=1}^N {\hat \omega _k^i{\boldsymbol{x}}_k^i},$ | (10) |
| $ {P_k}=\sum\limits_{i=1}^N {\hat \omega _k^i({{{\boldsymbol{\hat x}}}_k} - {\boldsymbol{x}}_k^i)} {({{\boldsymbol{\hat x}}_k} - {\boldsymbol{x}}_k^i)^{\rm T}}{。}$ | (11) |
粒子滤波最常见的问题就是粒子退化和贫化,即经过若干次递推,少数粒子的权重很高,这些粒子被反复选择,最终导致滤波效果不良甚至发散。为了克服这个问题,本文采用高斯分布来构造重要性密度函数
| $ \!N({{\boldsymbol{x}}_k};{{\boldsymbol{\mu }}_k}, {{\boldsymbol{\delta }}_k\!})\!=\! {(2\pi)^{ - m/2}}{\left| {{{\boldsymbol{\delta }}_k}} \right|^{ - 1/2}}\! \times\! {e^{(- \frac{1}{2}{{({{\boldsymbol{\!x\!}}_k} - {{\boldsymbol{\mu }}_k})}^{\rm T}}{\boldsymbol{\delta }}_k^{ - 1}({{\boldsymbol{x}}_k} - {{\boldsymbol{\mu }}_k}))}}\!。\!\!\!\!\!\!\! $ | (12) |
式中:m为高斯函数的维数;
系统后验概率密度的估计为:
| $ \hat p({{\boldsymbol{x}}_k}|{{\boldsymbol{Z}}^k})=N({{\boldsymbol{x}}_k};{{\boldsymbol{\mu }}_k}, {{\boldsymbol{\delta }}_k})。$ | (13) |
高斯粒子滤波的具体算法如下:
1)初始化
从
2)确定粒子权值并归一化
| $ \omega _k^i=\omega _{k - 1}^i\frac{{p({{\boldsymbol{z}}_k}|{\boldsymbol{x}}_k^i)p({\boldsymbol{x}}_k^i|{\boldsymbol{x}}_{k - 1}^i)}}{{q({\boldsymbol{x}}_k^i|{\boldsymbol{x}}_{k - 1}^i, {{\boldsymbol{Z}}^k})}},$ | (14) |
| $ \hat \omega _k^i=\omega _k^i/\sum\limits_{i=1}^N {\omega _k^i}。$ | (15) |
3)估计状态的均值和方差
| $ {\mu _k}=\sum\limits_{i=1}^N {\hat \omega _k^i{\boldsymbol{x}}_k^i},$ | (16) |
| $ {\Sigma _k}=\sum\limits_{i=1}^N {\hat \omega _k^i({{{\boldsymbol{\hat x}}}_k} - {\boldsymbol{x}}_k^i)} {({{\boldsymbol{\hat x}}_k} - {\boldsymbol{x}}_k^i)^{\rm T}}。$ | (17) |
4)更新粒子
①直接对
②由重要性密度函数即状态转移概率分布得k+1时刻的粒子集
5)返回第2步
1.4 改进高斯粒子滤波通常情况下,高斯粒子滤波的重要性密度函数
| $ q({{\boldsymbol{x}}_{0:k}}|{{\boldsymbol{Z}}^k})N({{\boldsymbol{x}}_{0:k}}|{{\boldsymbol{\bar \mu }}_k}, {{\boldsymbol{\bar \Sigma }}_k}),$ | (18) |
其中:
| $ {{\boldsymbol{\bar \mu }}_k}=\frac{1}{N}\sum\limits_{i=1}^N {{\boldsymbol{x}}_{k|k - 1}^i} \;\;({\boldsymbol{x}}_{k|k - 1}^i=f({\boldsymbol{x}}_{k - 1}^i)),$ | (19) |
| $ {{\boldsymbol{\bar \Sigma }}_k}=\frac{1}{N}\sum\limits_{i=1}^N {{\boldsymbol{x}}_{k|k - 1}^i} {\boldsymbol{x}}_{k|k - 1}^{i{\rm T}} - {{\boldsymbol{\bar \mu }}_k}{\boldsymbol{\bar \mu }}_k^{\rm T}+{\boldsymbol{Q}}。$ | (20) |
这样的高斯分布虽然与系统状态的后验概率密度有着很大的相似性,但由于没有融合实时测量值,所以当过程噪声较大时,重要密度函数还和真实分布有着较大区别,从而导致滤波效果不良,所需粒子规模和算法运行时间会相对较长。
为了使重要性密度函数更加接近真实分布,采用Unscented卡尔曼滤波来产生高斯分布,由于Unscented卡尔曼本身能融合有效观测信息,能够将采样粒子推向高似然区,所以可以有效的近似真实分布,并且将Unscented卡尔曼滤波引入高斯粒子滤波,不存在当过程噪声
Unscented卡尔曼滤波是基于UT变换的Sigma卡尔曼滤波,其实现过程具体如下:
1)初始化
| $ {{\boldsymbol{\hat x}}_0}=E[{{\boldsymbol{x}}_0}],$ | (21) |
| $ {{\boldsymbol{P}}_0}=E\left[{({{\boldsymbol{x}}_0}-{{{\boldsymbol{\hat x}}}_0}){{({{\boldsymbol{x}}_0}-{{{\boldsymbol{\hat x}}}_0})}^{\rm T}}} \right]。$ | (22) |
2)样点计算
运用对称采样策略,计算2n+1个采样点
| $ \left\{ {\begin{array}{*{20}{l}} {{{\boldsymbol{\xi }}_{0, k - 1}}={{{\boldsymbol{\hat x}}}_{k - 1}}},\\ {{{\boldsymbol{\xi }}_{i, k - 1}}={{{\boldsymbol{\hat x}}}_{k - 1}}+{{\left({\sqrt {(n+\kappa){{\boldsymbol{P}}_k}} } \right)}_i}},\\ {{{\boldsymbol{\xi }}_{i+n, k - 1}}={{{\boldsymbol{\hat x}}}_{k - 1}} - {{\left({\sqrt {(n+\kappa){{\boldsymbol{P}}_k}} } \right)}_i}},\end{array}} \!\!\right.i=1, 2, \cdot \cdot \cdot, n,$ | (23) |
对应的Sigma点的权值为:
| $ {\boldsymbol{W}}_i^m={\boldsymbol{W}}_i^c=\left\{ {\begin{array}{l} {k/(n+k)\;\;i=0},\\ {1/[2(n+k)]\;\;i \ne 0}。\end{array}} \right.$ | (24) |
式中,κ为用来调节Sigma点与
3)时间更新
由(2)得到的Sigma点,通过状态转移方程
| $ {\gamma _{i, k|k - 1}}=f({\xi _{i, k - 1}})+{q_{k - 1}}\;\;i=0, 1, \cdot \cdot \cdot, L, $ | (25) |
| $ \begin{split}\\[-12pt] {{{\boldsymbol{\hat x}}}_{k|k - 1}}\!=\! \sum\limits_{i=0}^L {{\boldsymbol{W}}_i^m{{\boldsymbol{\gamma }}_{i, k|k - 1}}} \!=\!\sum\limits_{i=0}^L {{\boldsymbol{W}}_i^m{{\boldsymbol{f}}_{k - 1}}({{\boldsymbol{\xi }}_{i, k - 1}})}+{{\boldsymbol{q}}_{k - 1}},\end{split} $ | (26) |
| $ \begin{split}\\[-12pt] {P_{k|k - 1}}=\sum\limits_{i=0}^L {W_i^c}({\gamma _{i, k|k - 1}} - \\ {{\hat x}_{k\backslash k - 1}}){({\gamma _{i, k|k - 1}} - {{\hat x}_{k\backslash k - 1}})^{\rm{T}}}+{Q_{k - 1}}。\end{split} $ | (27) |
4)测量更新
同样运用对称采样策略,由
| $ {{\boldsymbol{\hat z}}_{k|k - 1}}=\sum\limits_{i=0}^L {{\boldsymbol{W}}_i^m{{\boldsymbol{h}}_k}({{\boldsymbol{\xi }}_{i, k|k - 1}})+{{\boldsymbol{r}}_k},} $ | (28) |
| $ \!\begin{array}{c} \!\!{{\boldsymbol{P}}_{{{{\boldsymbol{\tilde z}}}_k}}}\!\!=\!\! \sum\limits_{i=0}^L {{\boldsymbol{W}}_i^c({{\boldsymbol{\chi }}_{i, k|k - 1}}\! -\! {{{\boldsymbol{\hat z}}}_{k|k - 1}}){{({{\boldsymbol{\chi }}_{i, k|k - 1}} \!-\! {{{\boldsymbol{\hat z}}}_{k|k - 1}})}^{\rm T}}}\!\!+\! {{\boldsymbol{R}}_k},\!\!\!\! \end{array} $ | (29) |
| $ {{\boldsymbol{P}}_{{{{\boldsymbol{\tilde x}}}_k}{{{\boldsymbol{\tilde z}}}_k}}}=\sum\limits_{i=0}^L {{\boldsymbol{W}}_i^c({{\boldsymbol{\xi }}_{i, k|k - 1}} - {{{\boldsymbol{\hat x}}}_{k|k - 1}})} {({{\boldsymbol{\chi }}_{i, k|k - 1}} - {{\boldsymbol{\hat z}}_{k|k - 1}})^{\rm T}},$ | (30) |
| $ {{\boldsymbol{\hat x}}_k}={{\boldsymbol{\hat x}}_{k|k - 1}}+{{\boldsymbol{K}}_k}({{\boldsymbol{z}}_k} - {{\boldsymbol{\hat z}}_{k|k - 1}}),$ | (31) |
| $ {{\boldsymbol{K}}_k}={{\boldsymbol{P}}_{{{{\boldsymbol{\tilde x}}}_k}{{{\boldsymbol{\tilde z}}}_k}}}{\boldsymbol{P}}_{{{{\boldsymbol{\tilde z}}}_k}}^{ - 1},$ | (32) |
| $ {{\boldsymbol{P}}_k}={{\boldsymbol{P}}_{k|k - 1}} - {{\boldsymbol{K}}_k}{{\boldsymbol{P}}_{{{{\boldsymbol{\tilde z}}}_k}}}{\boldsymbol{K}}_k^{\rm T}。$ | (33) |
至此,可得到经过Unscented卡尔曼滤波获得的高斯分布来作为重要概率密度函数:
| $ q({{\boldsymbol{x}}_{0:k}}|{{\boldsymbol{Z}}^k})N({{\boldsymbol{x}}_{0:k}}|{{\boldsymbol{\bar \mu }}_k}, {{\boldsymbol{\bar \Sigma }}_k})。$ | (34) |
其中
将上述高斯粒子滤波的步骤4中的重要性密度函数替换为式(34),即为本文提出的改进高斯粒子滤波。
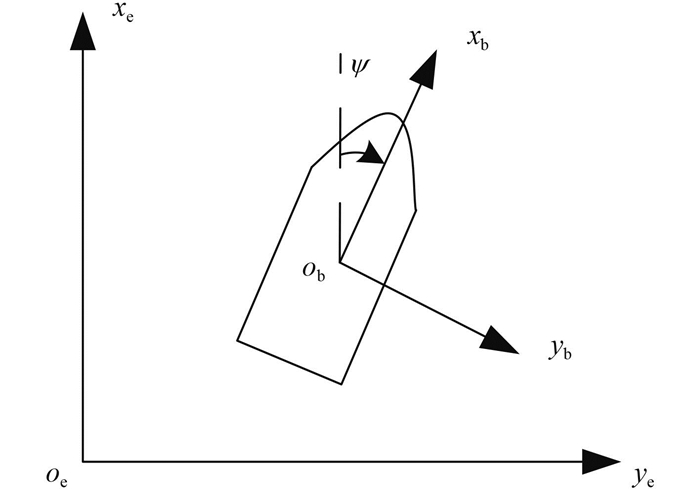
2 非线性状态估计器设计 2.1 船舶模型选取低速航行的动力定位船为研究对象,忽略横摇、纵摇和升沉运动,只考虑船的水平面运动,分别建立三自由度高频运动模型和低频运动模型。
|
图 1 东向位移测量值和估计值 Fig. 1 Ship's movement in the horizontal plane |
由于船的位姿和线速度分别在北东坐标系和船体坐标系下表述,所以要利用欧拉变换对其进行转换,转换关系为[14-15]:
| $ {\boldsymbol{\dot \eta }}={\boldsymbol{R}}(\psi){\boldsymbol{\nu }}。$ | (35) |
式中:
对于一大类水面船都可以用式(36)和式(37)表示的数学模型来描述其低频运动。
| $ {\boldsymbol{M\dot \nu }}+{\boldsymbol{D\nu }}={\boldsymbol{\tau }}+{{\boldsymbol{R}}^{\rm T}}(\psi){\boldsymbol{b}},$ | (36) |
| $ {\boldsymbol{\tau }}={{\boldsymbol{B}}_u}{\boldsymbol{u}},$ | (37) |
| $ {\boldsymbol{\dot b}}=- {{\boldsymbol{T}}^{ - 1}}{\boldsymbol{b}}+{{\boldsymbol{E}}_b}{{\boldsymbol{\omega }}_b}。$ | (38) |
式中,
| $ {\boldsymbol{M}}=\left[{\begin{array}{*{20}{c}} {m-{X_{\dot u}}} &0 &0\\ 0 &{m-{Y_{\dot v}}} &{m{x_G}-{Y_{\dot r}}}\\ 0 &{m{x_G} - {Y_{\dot r}}} &{{I_z} - {N_{\dot r}}} \end{array}} \right],$ | (39) |
| $ {\boldsymbol{D}}=\left[{\begin{array}{*{20}{c}} {-{X_u}} &0 &0\\ 0 &{-{Y_v}} &{-{Y_r}}\\ 0 &{ - {N_v}} &{ - {N_r}} \end{array}} \right]。$ | (40) |
本文采用2阶模型来描述由1阶波浪力引起的船舶运动和状态空间:
| $ \left[{\begin{array}{*{20}{c}} {{{{\boldsymbol{\dot \xi }}}_{\rm{1}}}}\\ {{{{\boldsymbol{\dot \xi }}}_{\rm{2}}}} \end{array}} \right]=\left[{\begin{array}{*{20}{c}} {\boldsymbol{0}} &{\boldsymbol{I}}\\ {{{\boldsymbol{\varOmega }}_{{\rm{21}}}}} &{{{\boldsymbol{\varOmega }}_{{\rm{22}}}}} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{{\boldsymbol{\xi }}_{\rm{1}}}}\\ {{{\boldsymbol{\xi }}_{\rm{2}}}} \end{array}} \right]+\left[{\begin{array}{*{20}{c}} {\boldsymbol{0}}\\ {{{\boldsymbol{E}}_{h2}}} \end{array}} \right]{{\boldsymbol{\omega }}_h},$ | (41) |
| $ {{\boldsymbol{\eta }}_h}=\left[{\begin{array}{*{20}{c}} {\boldsymbol{0}} &{\boldsymbol{I}} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{{\boldsymbol{\xi }}_1}}\\ {{{\boldsymbol{\xi }}_2}} \end{array}} \right]。$ | (42) |
式中,
动力定位中的测量系统通常只能获得船的位置和首向信息,本文设计一种基于改进高斯粒子滤波的非线性状态估计器,将高频运动滤除,并把低频运动反馈给控制系统。
观测方程如下:
| $ {\boldsymbol{y}}={\boldsymbol{\eta }}+{{\boldsymbol{\eta }}_h}+{{\boldsymbol{\omega }}_y}。$ | (43) |
式中:
结合上述三自由度船舶高频、低频模型,可以得到船舶动力定位状态空间表述:
| $ {\boldsymbol{\dot x}}={\boldsymbol{f}}({\boldsymbol{x}})+{\boldsymbol{Bu}}+{\boldsymbol{E\omega }},$ | (44) |
| $ {\boldsymbol{y}}={\boldsymbol{Hx}}+{\boldsymbol{\upsilon }}。$ | (45) |
式中:
| $ {\boldsymbol{f(x)}}=\left[{\begin{array}{*{20}{c}} {{\boldsymbol{\Omega \xi }}}\\ {{\boldsymbol{R}}\left({\psi+{\psi _h}} \right){\boldsymbol{v}}}\\ {-{{\boldsymbol{T}}^{-1}}{\boldsymbol{b}}}\\ {-{{\boldsymbol{M}}^{ - 1}}{\boldsymbol{Dv}}+{{\boldsymbol{M}}^{ - 1}}{{\boldsymbol{R}}^T}\left({\psi+{\psi _h}} \right){\boldsymbol{b}}} \end{array}} \right],$ | (46) |
| $ {\boldsymbol{B}}=\left[{\begin{array}{*{20}{c}} {{{\boldsymbol{0}}_{6 \times p}}}\\ {{{\boldsymbol{0}}_{3 \times p}}}\\ {{{\boldsymbol{0}}_{3 \times p}}}\\ {{{\boldsymbol{M}}^{-1}}{{\boldsymbol{B}}_u}} \end{array}} \right],$ | (47) |
| $ {\boldsymbol{E}}=\left[{\begin{array}{*{20}{c}} {{{\boldsymbol{E}}_{\rm{h}}}} &{{{\boldsymbol{0}}_{6 \times 3}}} &{{{\boldsymbol{0}}_{6 \times 3}}}\\ {{{\boldsymbol{0}}_{3 \times 3}}} &{{{\boldsymbol{0}}_{3 \times 3}}} &{{{\boldsymbol{0}}_{3 \times 3}}}\\ {{{\boldsymbol{0}}_{3 \times 3}}} &{{{\boldsymbol{E}}_{\rm{b}}}} &{{{\boldsymbol{0}}_{3 \times 3}}}\\ {{{\boldsymbol{0}}_{3 \times 3}}} &{{{\boldsymbol{0}}_{3 \times 3}}} &{{{\boldsymbol{E}}_{\rm{s}}}} \end{array}} \right],$ | (48) |
| $ {\boldsymbol{H}}=\left[{\begin{array}{*{20}{c}} {\boldsymbol{\Gamma }} &{{{\boldsymbol{I}}_{3 \times 3}}} &{{{\boldsymbol{0}}_{3 \times 3}}} &{{{\boldsymbol{0}}_{3 \times 3}}} \end{array}} \right],$ | (49) |
用1.5阶Ito-Taylor将过程方程离散化[16]:
| $\begin{split}\\[-12pt] {\boldsymbol{x}}\left({t+\delta } \right)=\underbrace {{\boldsymbol{x}}\left(t \right)+\delta {\boldsymbol{f}}\left({{\boldsymbol{x}}\left(t \right), t} \right)+\frac{1}{2}{\delta ^2}\left({{\nabla _0}{\boldsymbol{f}}\left({{\boldsymbol{x}}\left(t \right), t} \right)} \right)}_{{{\boldsymbol{f}}_d}\left({{\boldsymbol{x}}\left(t \right), t} \right)}{+}\\ \sqrt {\boldsymbol{Q}} \varepsilon+\left({\nabla {\boldsymbol{f}}\left({{\boldsymbol{x}}\left(t \right), t} \right)} \right){\boldsymbol{e}}{。}\quad \quad \quad \quad \quad \quad \end{split}$ | (50) |
在离散时间上,去除噪声的过程方程可表示为:
| $ \begin{split}\\[-12pt] {{\boldsymbol{f}}_d}\left({{\boldsymbol{x}}\left(t \right), t} \right)={\boldsymbol{x}}\left(t \right)+\delta f\left({{\boldsymbol{x}}\left(t \right), t} \right)+\\[5pt] \frac{1}{2}{\delta ^2}\left({{\nabla _0}{\boldsymbol{f}}\left({x\left(t \right), t} \right)} \right),\end{split} $ | (51) |
微分算符
| $ \!\begin{array}{c} \!\!\!\!{\nabla _0}=\frac{\partial }{{\partial t}} \!+\! \sum\limits_{i=1}^n {{{\boldsymbol{f}}_i}} \frac{\partial }{{\partial {{\boldsymbol{x}}_i}}}+\frac{1}{2}\!\sum\limits_{j, p, q=1}^n {\sqrt {{{\boldsymbol{Q}}_{p, j}}} } \sqrt {{{\boldsymbol{Q}}_{j, p}}} {{\boldsymbol{f}}_i}\frac{{{\partial ^2}}}{{\partial {{\boldsymbol{x}}_p}\partial {{\boldsymbol{x}}_q}}},\!\!\! \end{array} $ | (52) |
| $ {\nabla _j}=\sum\limits_{i=1}^n {\sqrt {{{\boldsymbol{Q}}_{ij}}} } \frac{\partial }{{\partial {{\boldsymbol{x}}_i}}}。$ | (53) |
至此,可采用改进高斯粒子滤波来进行船舶状态估计,算法流程如第1.3中描述。
3 仿真分析用于仿真实验的某动力定位船参数如表 1所示。
|
|
表 1 某动力定位船舶的部分船体参数 Tab.1 Part of one DP vessel's hull parameters |
选择低频运动模型的参数为:
| $ \begin{array}{*{20}{l}} {\boldsymbol{M}=\left[{\begin{array}{*{20}{c}} {2.641532 \times {{10}^7}}&0&0\\ 0&{3.345547 \times {{10}^7}}&{1.491735 \times {{10}^7}}\\ 0&{1.491735 \times {{10}^7}}&{6.520948 \times {{10}^{10}}} \end{array}} \right], }\\ {\boldsymbol{D}=\left[{\begin{array}{*{20}{c}} {2.220421 \times {{10}^4}}&0&0\\ 0&{2.220421 \times {{10}^5}}&{-1.774611 \times {{10}^6}}\\ 0&{-1.774611 \times {{10}^6}}&{7.150578 \times {{10}^8}} \end{array}} \right], } \end{array} $ |
取式(2-20)中的时间常数矩阵为:
| $ \boldsymbol{T}=\left[{\begin{array}{*{20}{c}} {2500}&0&0\\ 0&{2500}&0\\ 0&0&{2500} \end{array}} \right]. $ |
选取船舶高频运动模型的参数,相对阻尼系数
为了验证所设计估计器性能,选取CKF估计器作为对比,使用Matlab进行仿真,仿真总时长为200 s,在t=50 s处加入测量野值,仿真结果如图 2~图 6所示。
|
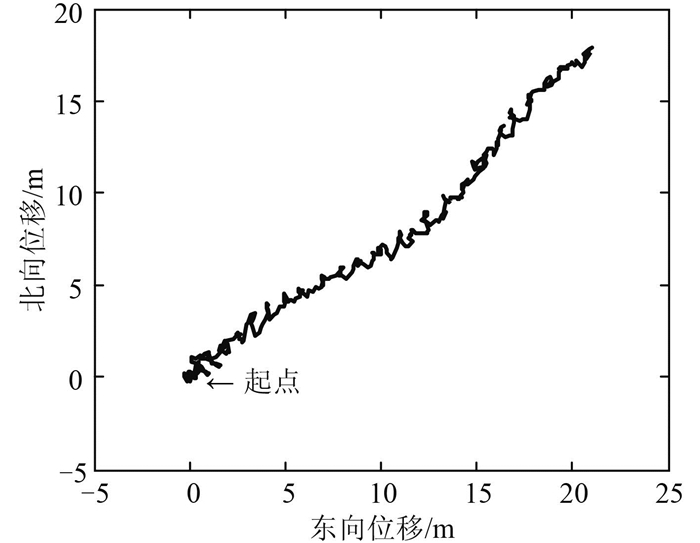
图 2 船舶水平面运动 Fig. 2 Horizontal position of vessel |
|
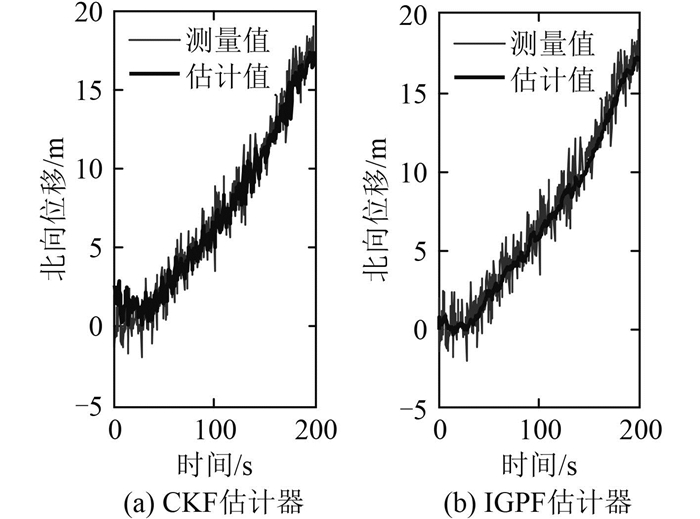
图 3 北向位移测量值和估计值 Fig. 3 The measurement and estimate data of ship surge displacement |
|
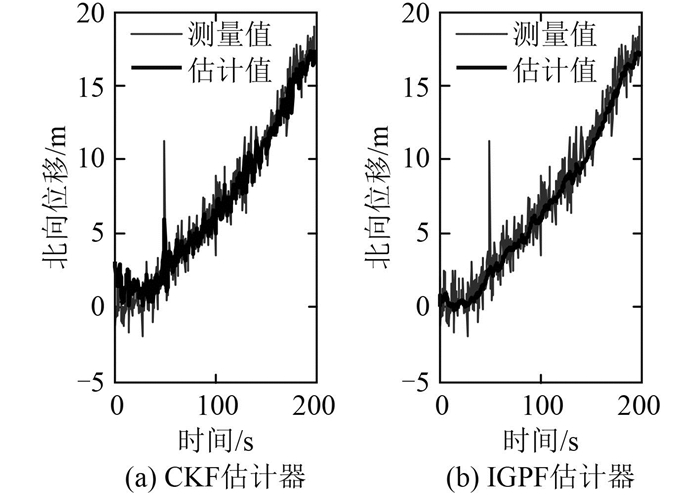
图 4 加野值时北向位移测量值和估计值 Fig. 4 The measurement and estimate data of ship surge displacement with outliers |
|
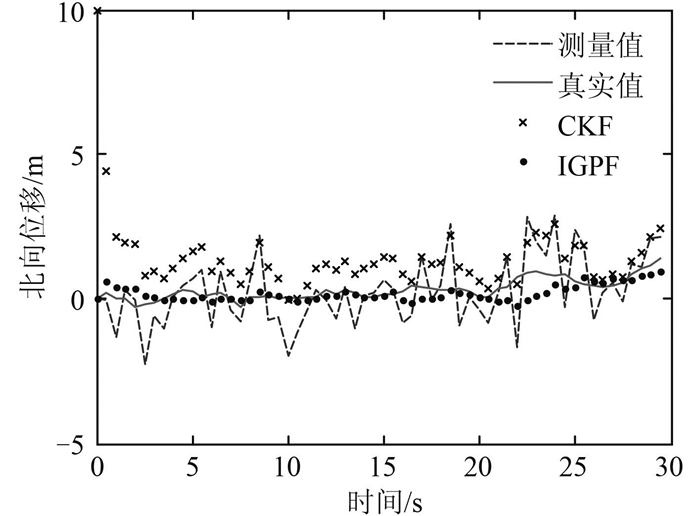
图 5 初始阶段状态估计器收敛速度对比 Fig. 5 Comparison of convergence speed in the first stage |
|
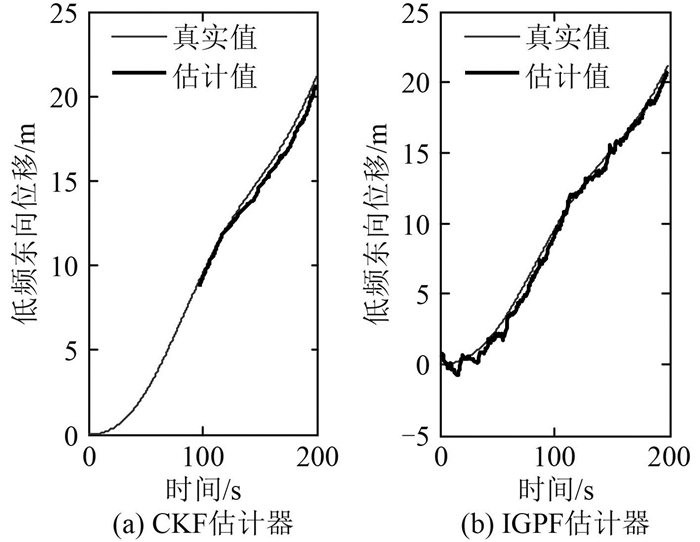
图 6 北向位移测量值和估计值 Fig. 6 The measurement and estimate data of ship surge displacement |
图 2描述了动力定位船在水平面内低速运动的轨迹;从图 3可看出,CKF和IGPF估计器均能估计出船舶状态,但IGPF的效果更加平滑;从图 4可知,IGPF可有效抵抗传感器测量野值的影响,状态估计值几乎没有波动,优于CKF;图 5给出开始30 s内的估计情况,CKF的收敛速度明显比IGPF慢,并且误差较大,而IGPF能快速跟跟踪船舶的真实状态;图 6显示在低频位移估计上,CKF和IGPF性能相近。
4 结语从仿真结果可看出,本文所采用的IGPF状态估计器和CKF估计器在白噪声环境下均能估计出船舶的状态,并且IGPF的估计曲线更为平滑,可以更好地反馈给控制器;当测量噪声中出现野值时,IGPF的估计值仍能接近真实值,有较好的鲁棒性,而CKF则随野值有较大波动。
综上所述,本仿真结果验证了IGPF观测器的有效性,并对噪声的变化有一定的鲁棒性。不足之处在于文中还未对非高斯噪声进行建模和仿真,有待进一步研究。
| [1] | SØRESEN A J. A survey of dynamic positioning control systems[J]. Annual Reviews in Control , 2011, 35 (1) :123–136. DOI: 10.1016/j.arcontrol.2011.03.008 |
| [2] |
边信黔, 付明玉, 王元慧.
船舶动力定位[M]. 北京: 科学出版社, 2011.
Bian Xin-qian, FU Ming-yu, WANG Yuan-hui. Dynamic positioning[M]. Beijing: Science Press, 2011. |
| [3] | SUNAHARA Y. An approximate method of state estimation for nonlinear dynamical systems[C]//Joint Automatic Control Conference. Colorado:University of Colorado, 1969. |
| [4] | JULIER S J, UHLMANN J K. New extension of the Kalman filter to nonlinear systems[C]//Proceedings of Aero Sence:the 11th International Symposium on Aerospace/Defense Sensing, Simulation and Controls. Orlando, Florida:SPIE, 1997. |
| [5] | ARASARATNAM I, HAYKIN S. Cubature Kalman filters[J]. IEEE Transactions on Automatic Control , 2009, 54 (6) :1254–1269. DOI: 10.1109/TAC.2009.2019800 |
| [6] | GILKS I L, BERZUINI C. Following a moving target-Monte Carlo inference for dynamic Bayesian models[J]. Journal of the Royal Statistical Society Series B:Statistical Methodology , 2001, 63 (1) :127–146. DOI: 10.1111/rssb.2001.63.issue-1 |
| [7] | SHREIDER Y A. Method of statistical testing:Monte Carlo method)[M]. Oxford: Pergamon Press, 1964. |
| [8] |
赵琳.
非线性系统滤波理论[M]. 北京: 国防工业出版社, 2012: 6-8.
ZHAO Lin. Nonlinear system filtering theory[M]. Beijing: National Defense Industry Press, 2012: 6-8. |
| [9] | VO B N, SINGH S, DOUCET A. Sequential Monte Carlo methods for multitarget filtering with random finite sets[J]. IEEE Transactions on Aerospace and Electronic Systems , 2005, 41 (4) :1224–1245. DOI: 10.1109/TAES.2005.1561884 |
| [10] | MOHAMMADI A, ASIF A. Consensus-based distributed unscented particle filter[C]//Proceedings of 2011 IEEE Statistical Signal Processing Workshop (SSP). Nice:IEEE, 2011:237-240. |
| [11] |
曲彦文, 张二华, 杨静宇. 改进的无迹粒子滤波算法[J]. 控制理论与应用 , 2010, 27 (9):1152–1158.
QU Yan-wen, ZHANG Er-hua, YANG Jing-yu. Improved unscented particle filter[J]. Control Theory & Applications , 2010, 27 (9) :1152–1158. |
| [12] | ZHAO Y X, XING W, YUAN H R, et al. A collaborative control framework with multi-leaders for AUVs based on unscented particle filter[J]. Journal of the Franklin Institute , 2016, 353 (3) :657–669. DOI: 10.1016/j.jfranklin.2015.11.016 |
| [13] | KOTECHA J H, DJURIC P M. Gaussian particle filtering[J]. IEEE Transactions on Signal Processing , 2003, 51 (10) :2592–2601. DOI: 10.1109/TSP.2003.816758 |
| [14] |
李殿璞.
船舶运动与建模[M]. 北京: 国防工业出版社, 1999: 1-17.
LI Dian-pu. Ship motion and modeling[M]. Harbin: Harbin Engineering University Press, 1999: 1-17. |
| [15] | FOSSEN T I. Marine control systems:guidance, navigation and control of ships, rigs and underwater vehicles[M]. Trondheim, Norway: Marine Cybernetics, 2002. |
| [16] | KLOEDEN P E, PLATEN E. Higher-order implicit strong numerical schemes for stochastic differential equations[J]. Journal of Statistical Physics , 1992, 66 (1/2) :283–314. |
 2016, Vol. 38
2016, Vol. 38
