小水线面双体船[1](Small Water-plane Area TwinHull Ship,SWATH)是近年来发展起来的一种高性能船型,具有常规双体船甲板面积大横稳性好的特点;同时凭借其水线面处流线型的支柱体,使此类船型的耐波性,高速航行时的阻力性能得到很大的提升。对于常规的船体,由于水线面面积较大从而纵倾力恢复力矩也较大,可与水动力纵倾力矩抵消一部分,减缓船体相对于水面的攻角。然而,SWATH航行时其左右下潜体将会受到纵倾力矩的作用,该力矩与航速的平方成正比。当船体的航速增大时,下潜体所受到的纵倾力矩将会迅速增大[2]。而狭窄的水线面面积则使得SWATH获得的恢复力矩也很小,当纵向恢复力矩不足以抵抗其所受到的纵倾力矩时,船体在纵向方向上的运动便易出现失稳现象。显然,船体失稳将使船体的安全性、适航性、舒适度直接下降,还有可能导致其他船舶设备无法正常适用。因此,必须采取有效的措施来保证SWATH运动的稳定性。
通过资料发现,由于SWATH船在美国、日本、德国等发达国家设计开发的时间较早,其姿态控制系统的技术水平较高,采用2对角度均能自动控制的鳍,同时控制SWATH的横摇、纵摇和垂荡等运动。近年来的研究和工程实践表明,稳定鳍对于提高小水线面双体船的纵向稳定性具有十分良好的效果。鳍工作的基本原理是船体在波浪中航行的纵向运动,在固定鳍上依靠船体自身的纵摇及该处的垂向运动产生的攻角引起的动升阻尼力矩,始终与舰船纵向运动方向相反,这样首尾鳍组合将产生较大的纵向运动稳定力矩,以达到减缓纵向运动的目的。考虑在支柱体内侧首尾处安装2对固定鳍,以改善其纵向运动性能。
1 船舶纵向运动方程虽然船体在波浪中的运动是相互影响的六自由度摇荡运动,但工程中在求解船体的运动时往往将运动进行解耦处理[3],以便提高计算效率。纵向运动和横向运动之间的藕合影响很小,可以忽略。在纵向运动中,由于进退运动对升沉和纵摇运动的藕合作用较小,通常亦予以忽略。加装中固定式减摇鳍目的主要是为了改善目标船的纵向运动性能。本文着重研究目标船型的纵向运动,尤其是升沉和纵摇运动。
当以随船坐标系为参考系时升沉与纵摇耦合的2阶线性微分方程:
| $ \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} (M+{A_{33}})\ddot z+{B_{33}}\dot z+{C_{33}}z+{A_{35}}\ddot \theta+{B_{35}}\dot \theta+{C_{35}}\theta=\\[4pt] {F_{zc}}\cos {\omega _e}t+{F_{zs}}\sin {\omega _e}t ,\end{array}\\[12pt] \begin{array}{l} ({J_{\theta \theta }}+{A_{55}})\ddot \theta+{B_{55}}\dot \theta+{C_{55}}\theta+{A_{53}}\ddot z+{B_{53}}\dot z+{C_{53}}z=\\[4pt] {M_{\theta c}}\cos {\omega _e}t+{M_{\theta s}}\sin {\omega _e}t 。\end{array} \end{array}} \right. $ | (1) |
其中:M为船体和鳍总重量;Jθθ为带鳍船体的纵向转动惯量。
式(1)中A33,B33,…,A55,B55,…,为船体的水动力系数。
2 纵向运动方程的修正在小水线面双体船的首尾支柱体内侧各安装一对固定式减摇鳍有助于减小船体的纵向运动。鳍抑制船的纵向运动,主要是基于鳍的流体动升力原理。当船在流体中以一定速度前进时,由于鳍与水流间形成一攻角,便可在鳍上产生一升力,这升力就可对抗船所受的外部干扰力。
设船体航速为U,鳍与来流之间的夹角为α,则单鳍上的产生的动升力[4]为:
| $ {F_f}=\frac{1}{2}\rho {U^2}SC_L^\alpha \alpha 。 $ | (2) |
其中,S为鳍面积,m2;CLα为鳍的升力系数对攻角的导数;U为航速,m/s;α为的来流与夹角;
鳍上攻角为
| $ \alpha=\theta+\left[{\dot Z-{x_f}\dot \theta-\dot \zeta \left({{x_f}, 0, -{d_f}} \right)} \right]/U+{\alpha _0} 。 $ | (3) |
其中,θ为船体的纵摇角,
单个鳍上的升力可表示为:
| $ \begin{split} &{F^f}=\dfrac{1}{2}r{U^2}SC_L^a\{ q+[\dot z-x{}_fq-\\ & x({x^f}, {y^f}, -{d^f})]/U+{a_0}\}, \end{split} $ | (4) |
单个鳍上的升力矩可表示为:
| $ \begin{split} &{M^f}=- \dfrac{1}{2}{x^f}r{U^2}SC_L^a\{ q+[\dot z-x{}_fq-\\ & x({x^f}, {y^f}, -{d^f})]/U+{a_0}\}。 \end{split} $ | (5) |
单个鳍上的流体惯性力为:
| $ K=\left({{m_f}+\Delta {m_f}} \right)\left({\ddot z - {x_f}\ddot \theta } \right) , $ | (6) |
因此,由鳍产生的总的垂向水动力可表示为:
| $ {F_f}=L+K , $ | (7) |
由鳍产生的总的垂向水动力纵倾力矩可表示为:
| $ {M_f}=- {x_f}{F_f} , $ | (8) |
同时,Mf,Ff又可分别写成下列各种力之和:
| $ {F_f}=A_{33}^f\ddot z+B_{33}^f\dot z+A_{35}^f\ddot \theta+B_{35}^f\dot \theta+C_{35}^f\theta+{F_{fv}} \cdot {e^{ - j{\omega _e}t}} , $ | (9) |
| $ {M_f} \!=\! A_{55}^f\ddot \theta \!+\! B_{55}^f\dot \theta \!+\! C_{55}^f\theta \!+\! A_{53}^f\ddot z \!+\! B_{53}^f\dot z \!+\! {M_{fv}} \cdot {e^{ - j{\omega _e}t}} 。 $ | (10) |
因此可得:
| $ \begin{split} \\[-12pt] &A_{33}^f=2\left({{m_f}+\Delta {m_f}} \right)=\dfrac{\pi }{2}\rho \dfrac{{{l^2} \cdot {d^2}}}{{\sqrt {{l^2}+{d^2}} }}, \\ & A_{35}^f=- 2\left({{m_f}+\Delta {m_f}} \right){x_f}, A_{53}^f=- 2\left({{m_f}+\Delta {m_f}} \right)x_f^2, \\ & B_{33}^f=\rho USC_L^\alpha, \;B_{35}^f=- \rho USC_L^\alpha {x_f}, \\ & B_{55}^f=\rho USC_L^\alpha x_f^2, \;B_{53}^f=- \rho USC_L^\alpha {x_f}, \\ & C_{35}^f=\rho {U^2}SC_L^\alpha, \;C_{55}^f=- \rho {U^2}SC_L^\alpha {x_f}, \\ & {F_{fv}}=j\omega A\rho USC_L^\alpha {e^{ - k{d_f}}}{e^{\left({jk{x_f}\cos \beta } \right)}}+\dfrac{1}{2}\rho {U^2}SC_L^\alpha \cdot {\alpha _0}\\ & {{M^{fv}}=- 2 \times j\omega A\rho USC_{\rm{L}}^\alpha {x^f}{e^{ - kd}}{e^{(jk{x^f}\cos \beta)}}}- \\ & \quad\;{ \dfrac{1}{2}\rho {x_f}{U^2}SC_L^\alpha \cdot {\alpha _0}}。 \end{split} $ | (11) |
式中,xf为鳍的纵向位置,df为鳍的垂向位置,l和d分别为鳍的弦长和展长。
计算出首尾鳍的动升力修正系数(如B33f、B35f、C35f等),并将其添加至原纵向运动方程中即可到计及首尾鳍动升力修正后船体纵向运动方程[5]:
| $ \left\{ \begin{array}{l} (M+{A_{33}}+A_{33}^f)\ddot z+({B_{33}}+B_{33}^f)\dot z+\\[8pt] {C_{33}}z+({A_{35}}+A_{35}^f)\ddot \theta+({B_{35}}+B_{35}^f)\dot \theta+\\[8pt] ({C_{35}}+C_{35}^f)\theta=[{F_3}-{F_{fv}}]{e^{ - j\omega t}},\\[8pt] ({I_\theta }+{A_{55}}+A_{55}^f)\ddot \theta+({B_{55}}+B_{55}^f)\dot \theta+\\[8pt] {C_{33}}\theta+({A_{53}}+A_{53}^f)\ddot z+({B_{53}}+B_{53}^f)\dot z+\\[8pt] ({C_{53}}+C_{53}^f)z=[{F_5}-{F_{fv}}]{e^{ - j\omega t}}。 \end{array} \right. $ | (12) |
因此,首先要考虑计算鳍的动升力力修正系数。
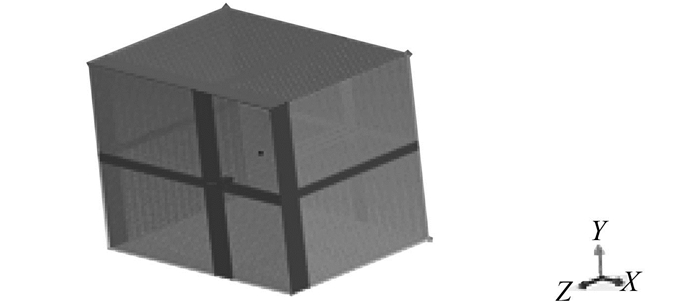
3 鳍的动升力修正系数计算本文采用Fluent软件计算鳍的动升力修正系数。计算流域在来流前方取5倍弦长,来流后方取10倍弦长,垂直于鳍的方向(即Y方向)5倍弦长,垂直于与鳍连接壁面的方向5倍弦长,如图 1所示。
|
图 1 ICEM-CFD中计算流域范围示意图 Fig. 1 Calculation basin in the ICEM-CFD |
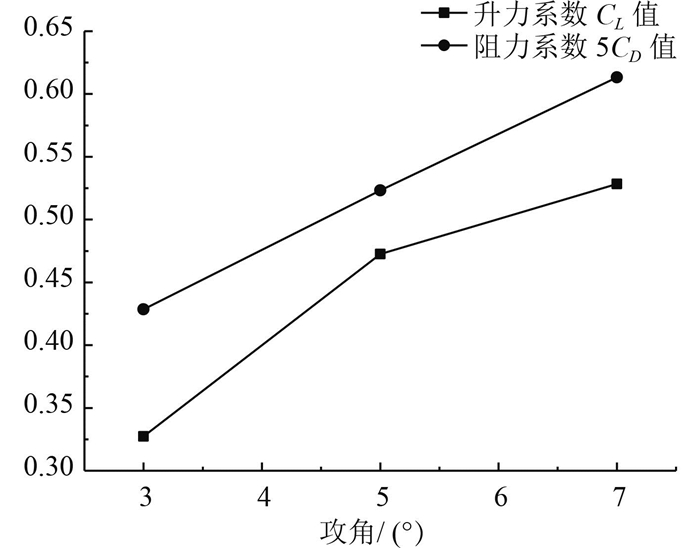
在小攻角范围内,升力系数CL与几何攻角呈线性关系。因此本文对鳍分别在攻角为3°,5°和7°时进行了计算(见图 2),通过计算各攻角下升力系数对攻角的导数求得动升力修正系数。
|
图 2 尾鳍的CL,CD与攻角的关系曲线 Fig. 2 The change of CL, CD with angle of attack |
由升力系数与攻角的关系曲线可知,当攻角较小时升力系数与攻角之间基本成线性关系。故可用线性拟合升力系数CL与攻角的关系曲线,拟合得到的CL与攻角的函数关系表达式为:CL=2.645·α+0.290 8,其中攻角的单位为弧度。由于首鳍和尾鳍形状相似,首鳍的升力修正系数可与尾鳍作相似处理。基于以上计算结果,可得到目标船首尾鳍的动升力系数为2.645。
依据前文中鳍动升力修正系数的公式推导结果和相关参数,可求得目标船首尾鳍的动升力修正系数,具体计算结果如表 1所示。
|
|
表 1 首尾鳍动升力修正系数计算结果 Tab.1 The calculation results of fin lift coefficient |
本文采用三维势流软件COMPASS-WALCS-BASIC对目标船进行预报,并对有鳍和无鳍船体预报结果进行对比,分析鳍对目标船的运动预报结果影响。计算时,首先在MSC.PATRAN中建立目标船的三维外壳模型,再将鳍导入WALCS软件中,对目标船进行湿表面水动力网格划分,划分后的结果如图 3所示。

|
图 3 目标船水动力外壳 Fig. 3 Target ship hydrodynamic shell |
船体质量分布是求解运动方程时的必要条件。一般情况下,质量分布按站位分布即可,横向均认为重心在中心线上。由于目标船型为双体船,计算时我们选取多体质量模型来模拟其质量分布。现将目标船的质量沿船长均匀划分成20部分,沿船宽划分成4部分(每个片体1部分、连接桥2部分),即用由80个小质量块构成的质量模型来模拟目标船的质量分布。目标船的整体质量模型和质量块划分情况如图 4所示。

|
图 4 全船质量块划分 Fig. 4 Whole ship quality division |
1)规则波中带鳍SWATH运动响应预报
规则波计算时,计算航速取为13 kn,波浪入射角取为0°~180°,间隔为30°。
基于前述计算原理,可求得在修正后规则波中带首尾鳍的SWATH的运动响应。
规则波中的响应结果如表 2所示。
|
|
表 2 带鳍船体运动情况统计 Tab.2 Statistical analysis of ship motion with fin |
2)不规则波中带鳍SWATH运动响应预报
安装减摇鳍的目的主要是为了改善其纵向运动,因此,主要关注升沉和纵摇的预报结果,对纵摇和升沉的短期预报,结果如表 3所示。
|
|
表 3 不规则波中升沉、纵摇运动比较 Tab.3 Heave and pitch motion comparison on the irregular wave |
3)无鳍船体与带鳍船体运动响应比较
无鳍与有鳍船体在规则波中的预报结果对比如表 4所示。
|
|
表 4 无鳍船体与带鳍船体运动RAO情况统计 Tab.4 Statistical analysis of the RAO condition of the hull with fins and with no fins |
由表中数据可知,横向运动如横荡、横摇有一定幅度的变小,这是因为鳍的存在增加了船体横向运动时的阻尼力矩及阻尼恢复力矩,但横向力臂较小,影响不是很大。纵向运动如纵摇、升沉变化很大,这是因为鳍上产生的动升力阻尼力矩与船体运动方向相反,可以很好地抑制船体纵向运动。纵荡、首摇几乎无变化,主要是鳍对其运动没有产生有效阻尼力矩的结果。
不规则波下的短期预报结果如表 5所示。
|
|
表 5 无鳍与带鳍船体升沉、纵摇短期预报比较 Tab.5 Short term prediction value of the heave and pitch between hull with fins and without fins |
由表 5可知,升沉幅值减小约7%,纵摇幅值减小约12%,有鳍船体的升沉和纵摇运动幅值均比无鳍船体有了很大的改善。这说明加装固定式首尾鳍对于减小船体的升沉和纵摇有益。且随着海况的增大,纵摇的减摇效果越来越好,8级海况下减摇效果可达17%左右。
从长期预报也可看到上面类似的结果。首尾鳍主要对船舶的纵向运动减摇效果明显,都达到了10%以上,对于纵荡、横荡等其他自由度的运动减摇效果不是很明显。
4)首尾鳍垂向速度和加速度研究
除了船舶六自由度的运动外,船舶运动的速度和加速度也是关注的重点。由WALCS可输出速度加速度计算结果,为了便于对比选择首尾处作为速度及加速度的计算点。
|
|
表 6 无鳍船体与带鳍船体运动长期预报值对比 Tab.6 Long term prediction value between hull with fins and with no fins |
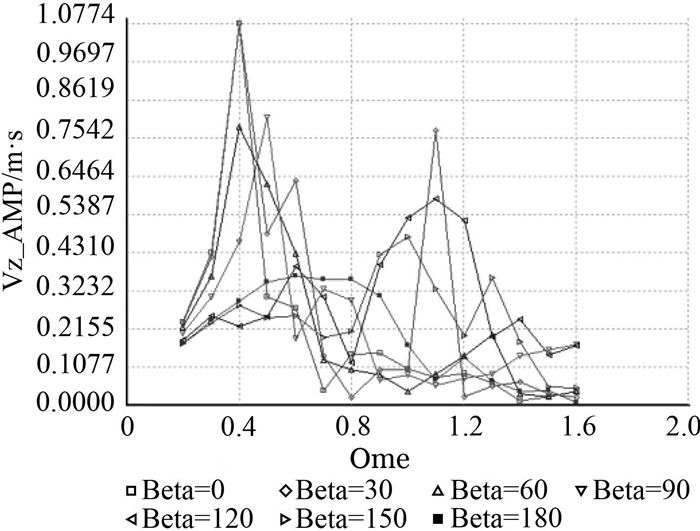
规则波中,首鳍和尾鳍的垂向速度和垂向加速度RAO曲线如图 5~图 8所示,计算结果如表 7所示。
|
图 5 首鳍垂向速度RAO曲线 Fig. 5 RAO curve of vertical velocity of head fill |
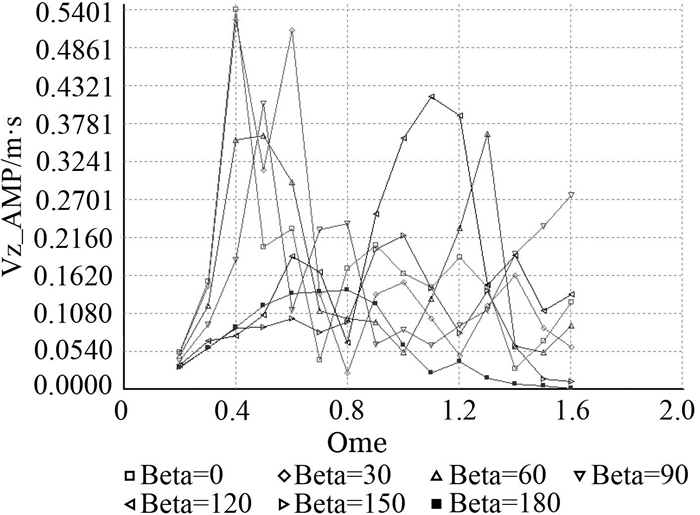
|
图 6 首鳍垂向加速度RAO曲线 Fig. 6 RAO curve of vertical acceleration of head fin |
|
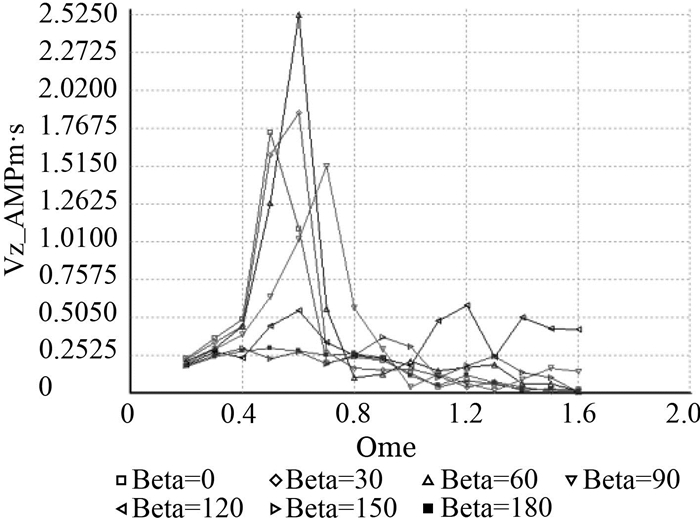
图 7 尾鳍垂向速度RAO曲线 Fig. 7 RAO curve of vertical velocity |
|
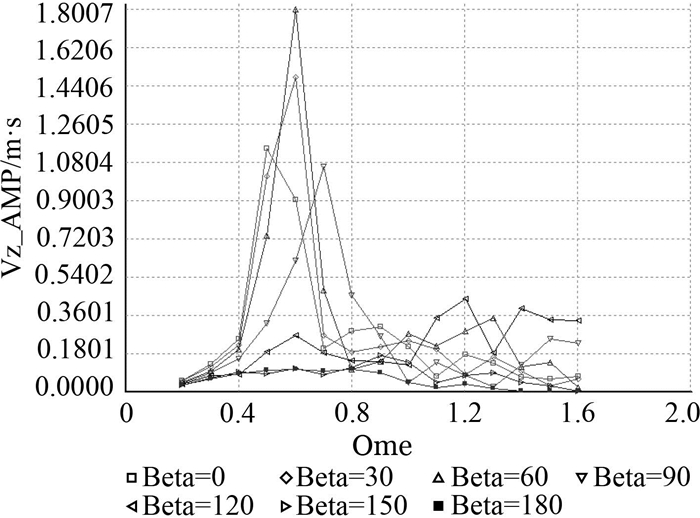
图 8 首尾鳍垂向速度和加速度规则波计算结果 Fig. 8 Vertical velocity and acceleration calculation results on fins |
|
|
表 7 首尾鳍垂向速度和加速度规则波计算结果 Tab.7 Vertical velocity and acceleration calculation results on fins |
|
|
表 8 无鳍船体首尾垂向速度和加速度规则波结果 Tab.8 Vertical velocity and acceleration calculation results with no fins |
由以上计算结果可知,有鳍船体相对于无鳍船体加速度大大降低,减少可达20%以上,速度也有一定程度的减小。首鳍的垂向速度和垂向加速度均在迎浪即0°浪向下达到最大,对应波浪圆频率为0.4 rad/s。尾鳍的垂向速度和垂向加速度均在斜浪即60°浪向下达到最大,对应波浪圆频率为0.6 rad/s。
5 结语1)本文根据由鳍产生的水动力系数对船舶纵向运动方程进行修正,通过WALCS软件进行运动预报。预报结果表明,安装固定式减摇鳍之后,船体纵向运动改善明显,尤其纵摇和升沉运动,在航速13 kn时,减摇效果达到10%以上,首尾加速度减小达20%以上。可见,安装固定式减摇鳍在理论上可行,能够很好地改善纵向运动。
2)计算鳍的水动力系数时,没有考虑鳍与船体的相互作用,不可避免的产生误差,需要从理论方面进一步完善。
| [1] |
林伟国, 朱云翔, 范井峰, 等. 小水线面双体船的发展及在海军舰船领域中的应用前景[J]. 船舶 , 2007, 18 (3):1–5.
LIN Wei-guo, ZHU Yun-xiang, FAN Jing-feng, et al. Development of small waterplane area twin hull and its application prospect in navy[J]. Ship & Boat , 2007, 18 (3) :1–5. |
| [2] |
戴遗山, 段文洋.
船舶在波浪中运动的势流理论[M]. 北京: 国防工业出版社, 2008.
DAI Yi-shan, DUAN Wen-yang. Potential flow theory of ship motions in waves[M]. Beijing: National Defence Industry Press, 2008. |
| [3] |
蔡新功, 李积德, 刘亚东, 等. 加装减纵摇组合附体舰船运动预报[J]. 水动力学研究与进展 , 2003, 18 (2):148–155.
CAI Xin-gong, LI Ji-de, LIU Ya-dong, et al. Prediction of motion of ships with built-up stabilizing appendage[J]. Journal of Hydrodynamics , 2003, 18 (2) :148–155. |
| [4] | LEE C M, CURPHEY R M. Prediction of motion, stability, and wave load of small-waterplane-area, twin-hull ships[C]//Presented at the Annual Meeting 1977. Jersey City, NJ:Society of Naval Architects and Marine Engineers, 1977:94-130. |
| [5] | SALVESEN N, TUCK E O, FALTINSEN O. Ship motions and sea loads[C]//Advance Copy of Paper to be Presented at the Annual Meeting 1970. New York:Society of Naval Architects and Marine Engineers, 1970(78):250-287. |
 2016, Vol. 38
2016, Vol. 38
