2. 武汉第二船舶设计研究所, 湖北 武汉 430064
2. Wuhan Second Ship Design and Research Institute, Wuhan 430064, China
有关光滑平板声辐射特性研究的文献比较多。其中,Laulagent[1]给出了求解简支矩形板声辐射问题的基本方法:首先,将外力和平板的振动位移按照简支板的模态振型级数展开;接着利用Green函数求出声场中任意一点的辐射声压;最后,进一步通过求解结构的运动控制方程便可对简支板进行声振特性分析。当边界条件不同时,Park[2]和Berry等[3]指出可以用弹簧和扭簧来等效代替边界支撑对矩形平板所产生的反力和反力矩作用。固支、简支、自由和其他边界条件可以通过不断调整等效弹簧和扭簧的刚度来模拟。接着便可采用Hamilton原理和Rayleigh-Ritz法得到其振动位移和声辐射功率。
针对周期性结构波动和声学行为研究比较深入的是英国南安普顿大学的学者们。Mead[4]系统综述了该大学于1964-1995年期间有关波在连续性周期结构中传播特征的研究,并且指出利用空间谐波展开法和傅里叶积分变换法都可分析周期加筋结构的声振行为。Mead[5]采用导纳法分析了具有周期性弹性支撑的无限长梁中的自由波运动。他指出这些自由波分成两部分,并分别沿x轴正向和负向传播从而形成了正向波和负向波。接着,Mead[6]从梁的振动控制方程出发,并结合周期性边界条件,研究了流体负载的周期支撑梁在简谐压力作用下的动态响应。基于空间谐波展开法,Mead和Pujara[7]首次研究了周期支撑梁中声波的传播问题,并指出该方法的数值截断解收敛速度很快。为了考虑流体载荷的影响,Mead和Mallik[8]采用相同方法研究了具有周期线支撑平板的声辐射问题,得到了令人满意的结果。Mathur等[9]基于空间谐波展开法建立了声波透射周期加筋板的理论分析模型,但是他们并给出详细的数值解。Lee和Kim[10]在文献[7]基础上,通过将加强筋等效成弹簧和扭簧组合模型,并结合虚功原理给出了平行加筋板传声损失的解析表达式,通过数值计算研究了不同系统参数对平行加筋板隔声性能的影响规律。他们指出平行加筋板的传声损失曲线在低频段是刚度控制域,在高频段则是质量控制域,而阻尼主要影响共振频率处的传声损失。
Rumerman[11]研究了无限大周期加筋板中波传播和受迫振动的问题。他将周期加强筋对薄板的影响用离散、平行分布的线力和力矩代替,推导出简谐压力作用在平板上的精确解,然后采用叠加原理便得到任意载荷激励下的解。Mace[12-16]采用与之相似的处理方法,基于傅里叶变换,先研究了具有流体负载的平行加筋板中的自由波传播问题。在他的研究中,结构的振动控制方程被变换到了波数域中来求解,这样使研究问题得到了极大的简化,且若考虑流体负载作用时便能同时给出表征结构响应的表达式。接着,Mace[17]将自己的方法进一步拓展,研究了在流体负载和点激励和线激励作用下无限大单向加筋平板的动态响应。研究表明:在低频段,当加强筋间距远小于平板弯曲波波长时可以将加筋板等效简化为正交各向异性的平板。Maxit[18]采用离散傅里叶变换法求得了平行加筋板在点激励作用下的波数空间和物理空间中振动位移响应和辐射声压,并且给出了结构在波数域中的横向位移谱。不过他的方法理解和实施起来会比较困难。Maidanik[19]研究由周期刚性线支撑的无限大平板的声振特性发现:刚性支撑会在频率低于临界频率时增加平板的辐射效率。Lyon[20]和Nayak[21]通过研究得到了相同的规律,同时,Lyon[20]和Nayak[21]通过研究单根梁加强的平板的声振特性还发现:增大弹性梁的横向运动可以降低无限大平板的辐射效率。Romanov[22]和Evseev[23]通过研究由多个刚性线支撑加强平板的声辐射效率发现:相邻线支撑间平板是否共振直接决定辐射效率曲线的峰值。
本文以均匀流中无限大流体负载金属平板为研究对象,基于对流波动方程和对流边界条件,提出用傅里叶变换在波数域中求解无限大平板在机械点力激励下振动和声辐射响应的基本思路;然后基于此通过引入脉冲函数,并充分考虑加强筋弯曲和扭转运动,建立均匀流中无限大单向周期加筋平板的声振理论模型,给出一种方便数值编程计算的矩阵表达式;接着通过有效性分析来验证本文理论模型和数值计算方法的正确性;最后分析不同系统参数对结构振动和声辐射特性的影响规律。
1 理论模型及其数值求解 1.1 无限大光滑平板考虑如图 1所示的无限大光滑平板,坐标系x-y平面位于板厚中间,平板厚度为h,材料密度为ρ,弹性模量和泊松比分别为E和μ,剪切模量为G=E/2(1+μ)。平板的下表面受到简谐点力F0e-jωt的作用,上表面(x-y)存在匀速运动的理想流体,流体密度为ρ0,流体中的声速为c0,流体运动速度为U。在下面的公式推导过程中,简谐时间项e-jωt将被省略。
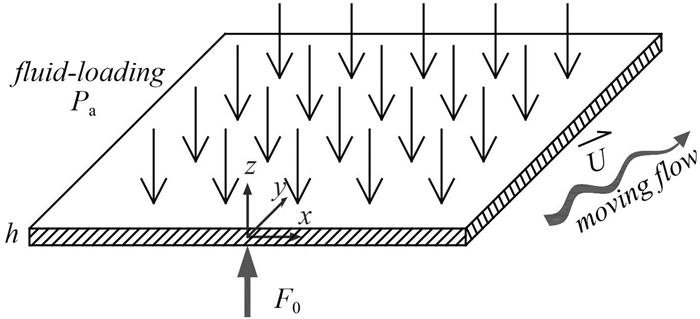
|
图 1 均匀流中无限大流体负载光滑平板的声辐射 Fig. 1 Sound radiation for an infinite fluid-loaded bare plate in moving flow |
平板上半空间内均匀流的声压Pa1(x,y,z)满足如下对流波动方程[24]:
| $ c_{0}^{2}{{\nabla }^{2}}{{P}_{a1}}={{(\frac{\partial }{\partial t}+U\cdot \nabla)}^{2}}{{P}_{a1}}, $ | (1) |
同时,声压在流固交界面上满足如下边界条件[24]:
| $ -{{\rho }_{0}}{{(\frac{\partial }{\partial t}+U\cdot \nabla)}^{2}}w={{\left.\frac{\partial {{P}_{a1}}}{\partial z} \right|}_{z=0}}, $ | (2) |
| $ U={{u}_{x}}i+{{u}_{y}}j=U\cos \varepsilon i+U\sin \varepsilon j. $ | (3) |
式中:
当无限大流体负载光滑平板受到外部简谐点力作用时,其声振耦合方程为:
| $ {{D}_{1}}w(x, y)={{F}_{0}}\delta({{x}_{0}})\delta({{y}_{0}})-{{P}_{a1}}(x, y, 0), $ | (4) |
| $ {{D}_{1}}=D(\frac{{{\partial }^{4}}}{\partial {{x}^{4}}}+2\frac{{{\partial }^{4}}}{\partial {{x}^{2}}\partial {{y}^{2}}}+\frac{{{\partial }^{4}}}{\partial {{x}^{4}}})-{{m}_{p}}\frac{{{\partial }^{2}}}{\partial {{t}^{2}}}. $ | (5) |
式中:D1为计及弹性力和惯性力在内的广义线性微分算子;D=Eh3/12(1-μ2)为平板的弯曲刚度;mp=ρh为平板单位面积上的密度;δ为Dirac delta函数;Pa1(x;y,0)为平板上表面处的壁面声压;F0为点激励力的幅值。
1.1.3 波数变换域中求解函数f(x,y)关于空间位置的Fourier变换及其逆变换定义为[16]:
| $ \tilde{f}(\alpha, \beta)=\int_{-\infty }^{+\infty }{\int_{-\infty }^{+\infty }{f(x, y)}}{{\text{e}}^{-\text{j}(\alpha x+\beta y)}}\text{d}x\text{d}y, $ | (6) |
| $ f(x, y)=\frac{1}{4{{\text{ }\!\!\pi\!\!\text{ }}^{2}}}\int_{-\infty }^{+\infty }{\int_{-\infty }^{+\infty }{\tilde{f}(\alpha, \beta)}}{{\text{e}}^{\text{j}(\alpha x+\beta y)}}\text{d}\alpha \text{d}\beta. $ | (7) |
下面将利用波数变换法求解以方程(1)和方程(4)分别为流体和结构运动控制方程,以方程(2)为边界条件的光滑平板的声振耦合问题。
1)根据式(3)可知,方程(1)和方程(2)可表示为:
| $ \begin{array}{l} [-15pt][\frac{{{\partial ^2}}}{{\partial {t^2}}}+2{u_x}\frac{{{\partial ^2}}}{{\partial x\partial t}}+2{u_y}\frac{{{\partial ^2}}}{{\partial y\partial t}}+u_x^2\frac{{{\partial ^2}}}{{\partial {x^2}}}+u_y^2\frac{{{\partial ^2}}}{{\partial {y^2}}}+\\ \;\;\;\;\;\;\;\;\;\;\;\;2{u_x}{u_y}\frac{{{\partial ^2}}}{{\partial x\partial y}}]{P_{a1}}=c_0^2(\frac{{{\partial ^2}}}{{\partial {x^2}}}+\frac{{{\partial ^2}}}{{\partial {y^2}}}+\frac{{{\partial ^2}}}{{\partial {z^2}}}){P_{a1}}, \end{array} $ | (8) |
| $ \begin{array}{l} {\rho _0}[\frac{{{\partial ^2}}}{{\partial {t^2}}}+2{u_x}\frac{{{\partial ^2}}}{{\partial x\partial t}}+2{u_y}\frac{{{\partial ^2}}}{{\partial y\partial t}}+u_x^2\frac{{{\partial ^2}}}{{\partial {x^2}}}+u_y^2\frac{{{\partial ^2}}}{{\partial {y^2}}}+\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;2{u_x}{u_y}\frac{{{\partial ^2}}}{{\partial x\partial y}}]w={\left.{\frac{{\partial {P_{a1}}}}{{\partial z}}} \right|_{z=0}}. \end{array} $ | (9) |
2)利用式(6)对方程(8)和方程(9)进行Fourier变换,可以得到均匀流中的波数域声压
| $ {{\tilde P}_{a1}}(\alpha, \beta, z)=\frac{{-{\rho _0}{\omega _1}^2{e^{-\lambda 1z}}}}{{{\lambda _1}\left({\alpha, \beta } \right)}}\tilde w\left({\alpha, \beta } \right), $ | (10) |
| $ {\lambda _1}(\alpha, \beta)=\left\{ \begin{array}{l} \sqrt {{\alpha ^2}+{\beta ^2}-{k_1}^2}, \;\;{\alpha ^2}+{\beta ^2} \ge {k_1}^2{\rm{, }}\\ -{\rm{j}}\sqrt {{k_1}^2-{\alpha ^2} - {\beta ^2}}, \;\;{\alpha ^2}+{\beta ^2} <{k_1}^2. \end{array} \right. $ | (11) |
式中:ω1=ω -(uxα+uyβ)为均匀流中的计算频率;k1=k0 -(Mxα+Myβ)为均匀流中的波数;Mx=ux/c0和My=uy/c0为均匀流在x及y方向上的马赫数;α=k1cosθsinφ和β=k1sinθsinφ分别为均匀流中声波在x及y方向上的波数。
通过上述表达式,均匀流中波数k1进而可表示为:
| $ {k_1}={k_0}/(1+{M_x}\cos \theta \sin \varphi+{M_y}\sin \theta \sin \varphi). $ | (12) |
式中:k0=ω/c0为静止流体中的波数;θ和φ分别为方位角和仰角,如图 2所示。
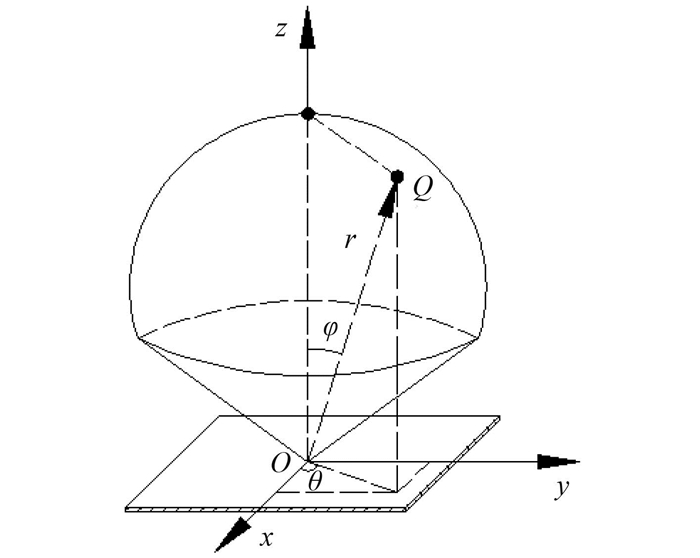
|
图 2 无限大点激励板中的球坐标示意图 Fig. 2 Sphere coordinate of the infinite point excited plate |
根据式(10)可得到波数域中光滑平板上表面(z=0)处的壁面声压为:
| $ {{\tilde P}_{a1}}(\alpha, \beta, 0)=-{\rho _0}{\omega _1}^2\tilde w(\alpha, \beta)/{\lambda _1}(\alpha, \beta){\rm{.}} $ | (13) |
3)利用式(6)对方程(4)进行Fourier变换,可得:
| $ \begin{array}{l} \left[{D{{({\alpha ^2}+{\beta ^2})}^2}-{m_p}{\omega ^2}} \right]\tilde w(\alpha, \beta)=\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{F_0}{{\rm{e}}^{ -j(\alpha {x_0}+\beta {y_0})}} -{{\tilde P}_{a1}}(\alpha, \beta, 0). \end{array} $ | (14) |
将式(13)代入方程(14)中,可将均匀流中平板在波数域的位移
| $ \tilde w(\alpha, \beta)={{\tilde w}_0}(\alpha, \beta){F_0}{{\rm{e}}^{-j(\alpha {x_0}+\beta {y_0})}}, $ | (15) |
| $ {{\tilde w}_0}(\alpha, \beta)=1/Z(\alpha, \beta), $ | (16) |
| $ Z(\alpha, \beta)=D{({\alpha ^2}+{\beta ^2})^2}-{m_p}{\omega ^2}-{\rho _0}{\omega _1}^2/{\lambda _1}(\alpha, \beta). $ | (17) |
式中:
考虑特殊情况,当流体静止时,ux=uy=0,即Mx=My=0,则k1=k0且ω1=ω。将其代入式(13)可得静止流体中流固交界面处的壁面声压表达式为:
| $ {{\tilde P}_a}(\alpha, \beta, 0)=-{\rho _0}{\omega ^2}\tilde w(\alpha, \beta)/\lambda(\alpha, \beta), $ | (18) |
其中:
| $ {\lambda _1}(\alpha, \beta)=\left\{ \begin{array}{l} \sqrt {{\alpha ^2}+{\beta ^2}-{k_0}^2}, {\alpha ^2}+{\beta ^2} \ge {k_0}^2{\rm{, }}\\ -{\rm{j}}\sqrt {{k_0}^2-{\alpha ^2} - {\beta ^2}}, {\alpha ^2}+{\beta ^2} <{k_0}^2. \end{array} \right. $ | (19) |
同时,当流体静止时,光滑平板的阻抗Z(α,β)可表示为:
| $ Z(\alpha, \beta)=D{({\alpha ^2}+{\beta ^2})^2}-{m_p}{\omega ^2}-{\rho _0}{\omega ^2}/\lambda(\alpha, \beta). $ | (20) |
根据式(15)~式(17),可以得到均匀流中光滑平板在波数域中的横向位移。然后,利用稳相法[16],可以求出图 2所示的球坐标系下均匀流中光滑平板的远场辐射声压为:
| $ \begin{array}{l} {P_{a1}}(r, \theta, \varphi)=\\ \frac{{-{\rho _0}{\omega _1}^2{{\rm{e}}^{-{\rm{j}}{k_1}r}}}}{{2{\rm{\pi }}r}}\int\limits_{-\infty }^{+\infty } {\int\limits_{ - \infty }^{+\infty } {w(x, y)} } {{\rm{e}}^{ - {\rm{j}}(\alpha x+\beta y)}}{\rm{d}}x{\rm{d}}y. \end{array} $ | (21) |
其中r为球面半径,表示机械点力作用点(即球坐标原点O)到声场点(球面上一参考点Q)的距离。
根据光滑平板波数域中的横向位移的表达式,可以将式(21)表示为:
| $ {P_{a1}}(r, \theta, \varphi)=\frac{{-{\rho _0}{\omega _1}^2{{\rm{e}}^{-{\rm{j}}{k_1}r}}}}{{2{\rm{\pi }}r}}\tilde w(\alpha, \beta), $ | (22) |
特别地,当流体静止时,光滑平板的远场辐射声压可表示为:
| $ {P_a}(r, \theta, \varphi)=\frac{{-{\rho _0}{\omega ^2}{e^{-{\rm{j}}{k_0}r}}}}{{2{\rm{\pi }}r}}\tilde w(\alpha, \beta){\rm{, }} $ | (23) |
根据光滑平板波数域中的远场辐射声压可以计算其远场辐射声压级(SPL)为:
| $ SPL=20{\log _{10}}\left| {{P_{a1}}/{P_0}} \right|. $ | (24) |
其中P0为参考声压,水中参考声压一般取P0=1 μPa。
1.2 单向加筋平板考虑如图 3所示的均匀流中无限大单向加筋平板,y方向上有一系列平行排列的加强筋沿着x方向等间距均匀分布,加强筋间距为L。假设平板和加强筋都为各向同性材料。当从平板下侧(x0,y0)位置处施加一单位简谐点激励平板或加强筋上时,会使得加筋平板产生振动继而向平板上侧的流场中辐射声压,同时流场中的声压也会影响加筋平板的运动。由于加筋平板结构在y轴方向上无限性,为了简便研究一般令y0=0。
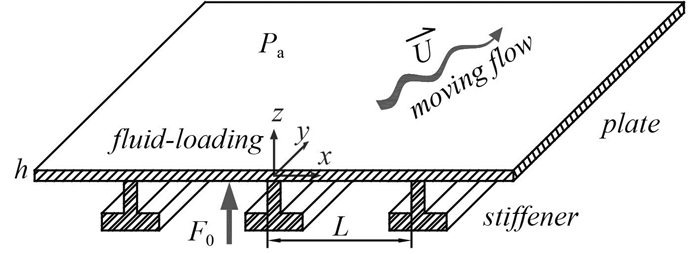
|
图 3 均匀流中的单向加筋板 Fig. 3 Unidirectionally stiffened fluid-loaded plate in moving flow |
为了让本文的研究更具一般性,建立的理论模型能同时研究运动和静止流体中单向加筋平板的声振特性。基于薄板理论,并引入脉冲函数来处理离散分布的加强筋,单向加筋平板的声振耦合方程将写成如下形式:
| $ \begin{array}{l} {D_1}\{ w(x, y)\}=-\sum\limits_{m=-\infty }^{+\infty } F(x, y)\delta(x-mL)+\sum\limits_{m=- \infty }^{+\infty } M(x, y)\delta '\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(x- mL)+{F_0}\delta({x_0})\delta({y_0})- {P_{a*}}(x, y, 0). \end{array} $ | (25) |
式中:F(x,y)δ(x-mL)和M(x,y)δ′(x-mL)分别为x=mL处的加强筋作用在平板上的反力和反力矩;Pa*(x,y,0)为平板上表面的广义壁面声压。当流体运动时,用符号Pa1表示;当流体静止时,用符号Pa表示。
1.2.2 加强筋的反力和反力矩当平板受到外力作用做弯曲运动时,加强筋也随之做受迫运动。为了研究方便,本文假设:1)平板与加强筋之间是线接触;2)加强筋具有对称截面且其中心轴线垂直于平板,故加强筋的弯曲和扭转运动之间耦合作用可以忽略。因此,基于Euler-Bernoulli梁理论,并结合平板和加强筋之间的位移连续条件可知做弯曲和扭转运动的加强筋的运动方程如下:
| $ {E_s}{I_s}\frac{{{\partial ^4}w}}{{\partial {y^4}}}+{\rho _s}{A_s}\frac{{{\partial ^2}w}}{{\partial {t^2}}}=F(x, y), $ | (26) |
| $ -{G_s}{J_s}\frac{{{\partial ^3}w}}{{\partial x\partial {y^2}}}-{\omega ^2}\rho {I_{os}}\frac{{\partial w}}{{\partial x}}=M(x, y). $ | (27) |
式中:Es,Gs,μs和ρs分别为加强筋材料的弹性模量、剪切模量及泊松比和密度;As,Is,Ios和Js分别为横截面面积、惯性矩、极惯性矩和横截面扭转常数。
1.2.3 波数变换域中求解根据图 1所示的单向加筋平板结构的周期特性,利用泊松求和公式,可以用空间谐波级数求和的形式来表示结构中的波数分量:
| $ \sum\limits_{m=-\infty }^{+\infty } {\delta(x-mL)}=\frac{1}{L}\sum\limits_{m=-\infty }^{+\infty } {{{\rm{e}}^{- j(\frac{{2m{\rm{\pi }}}}{L})x}}}. $ | (28) |
为了求解方程(25),需要对方程(25)~方程(27)左右两边做傅里叶变换,结合式(13)和式(18),同时应用泊松求和公式,可以得到下列表达式:
| $ \begin{array}{l} Z(\alpha, \beta)\tilde w(\alpha, \beta)={F_0}{{\rm{e}}^{-{\rm{j}}(\alpha {x_0}+\beta {y_0})}}-R(\beta)\sum\limits_{m=-\infty }^{+\infty } {\tilde w} \\ ({\alpha _m}, \beta)\alpha S(\beta)\sum\limits_{m=- \infty }^{+\infty } {{\alpha _m}\tilde w({\alpha _m}, \beta)} \end{array} $ | (29) |
| $ R(\beta)=\frac{1}{L}({E_s}{I_s}{\beta ^4}-{\omega ^2}{\rho _s}{A_s}), $ | (30) |
| $ S(\beta)=\frac{1}{L}({G_s}{J_s}{\beta ^2}-{\omega ^2}{\rho _s}{I_{os}}). $ | (31) |
式中:αm=α+2πm/L(m=-∞~+∞);R(β)和S(β)为加强筋的弯曲和扭转阻抗;Z(α,β)为流体负载平板的广义阻抗,可以由式(17)计算得到。
由方程(29)可以得到计算均匀流中单向加筋平板在波数域的横向位移的一般表示式为:
| $ \begin{array}{*{20}{l}} {\tilde w(\alpha, \beta)={{\tilde w}_0}(\alpha, \beta)[{F_0}{{\rm{e}}^{-{\rm{j}}(\alpha {x_0}+\beta {y_0})}}-R(\beta)\sum\limits_{m=-\infty }^{+\infty } \tilde w({\alpha _m}, \beta)- }\\ {\quad \quad \quad \alpha S(\beta)\sum\limits_{m=- \infty }^{+\infty } {{\alpha _m}\tilde w({\alpha _m}, \beta)}]{\rm{.}}} \end{array} $ | (32) |
其中
将方程(32)展开并做移项处理将得到下式:
| $ \begin{array}{l} \tilde w(\alpha, \beta)+{{\tilde w}_0}(\alpha, \beta)R(\beta)\zeta(\alpha, \beta)+{{\tilde w}_0}(\alpha, \beta)+\\ \alpha S(\beta)\xi(\alpha, \beta)={{\tilde w}_0}(\alpha, \beta)[{F_0}{{\rm{e}}^{-{\rm{j}}(\alpha {x_0}+\beta {y_0})}}], \end{array} $ | (33) |
其中ξ(α,β)和ζ(α,β)的表达式分别表示如下:
| $ \begin{array}{*{20}{l}} {\xi(\alpha, \beta)=\sum\limits_{m=-\infty }^{+\infty } {{\alpha _m}\tilde w({\alpha _m}, \beta)}, }\\ {\zeta(\alpha, \beta)=\sum\limits_{m=-\infty }^{+\infty } {\tilde w({\alpha _m}, \beta)} {\rm{.}}} \end{array} $ | (34) |
根据结构的周期特性可知,ξ(α,β)和ζ(α,β)满足下述关系式[18]:
| $ \xi(\alpha, \beta)=\xi({\alpha _m}, \beta), \;\;\zeta(\alpha, \beta)=\zeta({\alpha _m}, \beta), $ | (35) |
为了求解方程(33),令α=αm,并将其代入方程(33)可得:
| $ \begin{array}{l} \tilde w({\alpha _{m'}}, \beta)+{{\tilde w}_0}({\alpha _{m'}}, \beta)R(\beta)\zeta({\alpha _{m'}}, \beta)+{{\tilde w}_0}({\alpha _{m'}}, \beta), \\ {\alpha _{m'}}S(\beta)\xi({\alpha _{m'}}, \beta)={{\tilde w}_0}({\alpha _{m'}}, \beta)[{F_0}{{\rm{e}}^{-{\rm{j}}({\alpha _{m'}}{x_0}+\beta {y_0})}}], \end{array} $ | (36) |
将式(34)和式(35)代入方程(36)可得:
| $ \begin{array}{*{20}{l}} {\tilde w({\alpha _{m'}}, \beta)+{{\tilde w}_0}({\alpha _{m'}}, \beta)R(\beta)\sum\limits_{m=- \infty }^{+\infty } \tilde w({\alpha _m}, \beta)+{{\tilde w}_0}({\alpha _{m'}}, \beta), }\\ {S(\beta){\alpha _{m'}}\sum\limits_{m=- \infty }^{+\infty } {\alpha _m}\tilde w({\alpha _m}, \beta)={{\tilde w}_0}({\alpha _{m'}}, \beta)\left[{{F_0}{{\rm{e}}^{-{\rm{j}}({\alpha _{m'}}{x_0}+\beta {y_0})}}} \right].} \end{array} $ | (37) |
其中αm′=α+2πm′/L(m′=-∞~+∞)。
方程(37)是关于
| $ {[\boldsymbol{T}]_{M \times M}}{\{ \tilde w({\alpha _{m'}}, \beta)\} _{M \times 1}}={\{ {q_m}\} _{M \times 1}}. $ | (38) |
通过数值求解方程(38)可以得到单向加筋平板在波数域中的横向振动位移
方程(38)中的矩阵维数M等于2k+1,因此,k即使取一个较小的值时,也会使得矩阵的维数变得很大。为了叙述的方便,本文在介绍数值阶段方法时,令k=2,则m′的取值为m′=-2,-1,0,1,2。这样方程中的未知数为
| $ \left[{\begin{array}{*{20}{l}} {{T_{11}}{T_{12}}{T_{13}}{T_{14}}{T_{15}}}\\ {{T_{21}}{T_{22}}{T_{23}}{T_{24}}{T_{25}}}\\ {{T_{31}}{T_{32}}{T_{33}}{T_{34}}{T_{35}}}\\ {{T_{41}}{T_{42}}{T_{43}}{T_{44}}{T_{45}}}\\ {{T_{51}}{T_{52}}{T_{53}}{T_{54}}{T_{55}}} \end{array}} \right]\left[{\begin{array}{*{20}{l}} {\tilde w({\alpha _{-2}}, \beta)}\\ {\tilde w({\alpha _{-1}}, \beta)}\\ {\tilde w({\alpha _0}, \beta)}\\ {\tilde w({\alpha _1}, \beta)}\\ {\tilde w({\alpha _2}, \beta)} \end{array}} \right]=\left[{\begin{array}{*{20}{l}} {{q_{-2}}}\\ {{q_{-1}}}\\ {{q_0}}\\ {{q_1}}\\ {{q_2}} \end{array}} \right], $ | (39) |
其中系数矩阵和载荷向量中的各系数表示如下:
| $ \begin{array}{l} {T_{11}}=1+[R(\beta)+S(\beta){\alpha _{-2}}{\alpha _{-2}}]{{\bar w}_0}({\alpha _{ - 2}}, \beta)\text{,}\\[2pt] {T_{21}}=[R(\beta)+S(\beta){\alpha _{-1}}{\alpha _{-2}}]{{\bar w}_0}({\alpha _{ - 1}}, \beta)\text{,}\\[2pt] {T_{12}}=[R(\beta)+S(\beta){\alpha _{-2}}{\alpha _{-1}}]{{\bar w}_0}({\alpha _{ - 2}}, \beta)\text{,}\\[2pt] {T_{22}}=1+[R(\beta)+S(\beta){\alpha _{-1}}{\alpha _{-1}}]{{\bar w}_0}({\alpha _{ - 1}}, \beta)\text{,}\\[2pt] {T_{13}}=[R(\beta)+S(\beta){\alpha _{-2}}{\alpha _0}]{{\bar w}_0}({\alpha _{ - 2}}, \beta)\text{,}\\[2pt] {T_{23}}=[R(\beta)+S(\beta){\alpha _{-1}}{\alpha _0}]{{\bar w}_0}({\alpha _{ - 1}}, \beta)\text{,}\\[2pt] {T_{14}}=[R(\beta)+S(\beta){\alpha _{-2}}{\alpha _1}]{{\bar w}_0}({\alpha _{ - 2}}, \beta)\text{,}\\[2pt] {T_{24}}=[R(\beta)+S(\beta){\alpha _{-1}}{\alpha _1}]{{\bar w}_0}({\alpha _{ - 1}}, \beta)\text{,}\\[2pt] {T_{15}}=[R(\beta)+S(\beta){\alpha _{-2}}{\alpha _2}]{{\bar w}_0}({\alpha _{ - 2}}, \beta)\text{,}\\[2pt] {T_{25}}=[R(\beta)+S(\beta){\alpha _{-1}}{\alpha _2}]{{\bar w}_0}({\alpha _{ - 1}}, \beta)\text{,}\\[2pt] {T_{31}}=[R(\beta)+S(\beta){\alpha _0}{\alpha _{-2}}]{{\bar w}_0}({\alpha _0}, \beta)\text{,}\\[2pt] {T_{41}}=[R(\beta)+S(\beta){\alpha _1}{\alpha _{-2}}]{{\bar w}_0}({\alpha _1}, \beta)\text{,}\\[2pt] {T_{32}}=[R(\beta)+S(\beta){\alpha _0}{\alpha _{-1}}]{{\bar w}_0}({\alpha _0}, \beta)\text{,}\\[2pt] {T_{42}}=[R(\beta)+S(\beta){\alpha _1}{\alpha _{-1}}]{{\bar w}_0}({\alpha _1}, \beta)\text{,}\\[2pt] {T_{33}}=1+[R(\beta)+S(\beta){\alpha _0}{\alpha _0}]{{\bar w}_0}({\alpha _0}, \beta)\text{,}\\[2pt] {T_{43}}=[R(\beta)+S(\beta){\alpha _1}{\alpha _0}]{{\bar w}_0}({\alpha _1}, \beta)\text{,}\\[2pt] {T_{34}}=[R(\beta)+S(\beta){\alpha _0}{\alpha _1}]{{\bar w}_0}({\alpha _0}, \beta)\text{,}\\[2pt] {T_{44}}=1+[R(\beta)+S(\beta){\alpha _1}{\alpha _1}]{{\bar w}_0}({\alpha _1}, \beta)\text{,}\\[2pt] {T_{35}}=[R(\beta)+S(\beta){\alpha _0}{\alpha _2}]{{\bar w}_0}({\alpha _0}, \beta)\text{,}\\[2pt] {T_{45}}=[R(\beta)+S(\beta){\alpha _1}{\alpha _2}]{{\bar w}_0}({\alpha _1}, \beta)\text{,}\\[2pt] {T_{51}}=[R(\beta)+S(\beta){\alpha _2}{\alpha _{-2}}]{{\bar w}_0}({\alpha _2}, \beta)\text{,}\\[3pt] {q_{ - 2}}={{\bar w}_0}({\alpha _{ - 2}}, \beta)[{F_0}{{\rm{e}}^{-{\rm{j}}({\alpha _{-2}}{x_0}+\beta {y_0})}}]\text{,}\\[3pt] {T_{52}}=[R(\beta)+S(\beta){\alpha _2}{\alpha _{-1}}]{{\bar w}_0}({\alpha _2}, \beta)\text{,}\\[3pt] {q_{ - 1}}={{\bar w}_0}({\alpha _{ - 1}}, \beta)[{F_0}{{\rm{e}}^{-{\rm{j}}({\alpha _{-1}}{x_0}+\beta {y_0})}}]\text{,}\\[2pt] {T_{53}}=[R(\beta)+S(\beta){\alpha _2}{\alpha _0}]{{\bar w}_0}({\alpha _2}, \beta)\text{,}\\[2pt] {q_0}={{\bar w}_0}({\alpha _0}, \beta)[{F_0}{{\rm{e}}^{-{\rm{j}}({\alpha _0}{x_0}+\beta {y_0})}}]\text{,}\\[3pt] {T_{54}}=[R(\beta)+S(\beta){\alpha _2}{\alpha _1}]{{\bar w}_0}({\alpha _2}, \beta)\text{,}\\[3pt] {q_1}={{\bar w}_0}({\alpha _1}, \beta)[{F_0}{{\rm{e}}^{-{\rm{j}}({\alpha _1}{x_0}+\beta {y_0})}}]\text{,}\\[3pt] {T_{55}}=1+[R(\beta)+S(\beta){\alpha _2}{\alpha _2}]{{\bar w}_0}({\alpha _2}, \beta)\text{,}\\[3pt] {q_2}={{\bar w}_0}({\alpha _2}, \beta)[{F_0}{{\rm{e}}^{-{\rm{j}}({\alpha _2}{x_0}+\beta {y_0})}}]\text{。} \end{array} $ | (40) |
根据方程(39)可以求解出位移向量,进而根据
利用波数变换法和数值截断法计算得到的光滑平板和单向加筋平板的横向位移,结合(24)式,分析点激励作用下,系统参数对无限大光滑平板和单向加筋平板在静止流场和匀速流场中远场声辐射特性的影响规律。结构阻尼通过复弹性模量E(1+jη)计及,其中η为结构损耗因子,下文中分别用ηp和ηs表示平板和加强筋的损耗因子。
2.1 参数定义进行数值研究之前,需要先确定计算过程中所需用到的各种参数。本文数值计算中,令ηp=ηs=0.02,假设平板上半空间流体为水,其密度ρ0=1 000 kg/m3,水中声速c0=1 500 m/s,点激励力的幅值F0=1 N,作用点的位置为(x0,0),数值计算过程中,其值可取(0,0),(L/4,0),(L/3,0)和(L/2,0)。球坐标系中声压考察点Q的坐标为(r,θ,φ)=(50 m,45°,45°)。最后将得到的远场辐射声压级都换算成r=1 m处的声源级。如果没有特别说明上述所选定的参数在接下来的分析中将保持不变。在接下来的数值计算中,平板和加强筋都取相同的各向同性材料,如表 1所示。
|
|
表 1 各向同性平板的材料属性 Tab.1 Material properties of the isotropic plate |
为了便于与文献中的计算结果进行对比,在计算单向加筋平板的远场辐射声压级(SPL)时,加强筋的横截面定为对称的矩形截面。不同计算工况下的矩形截面加强筋的截面参数如表 2所示。
|
|
表 2 矩形截面加强筋 Tab.2 Cross-section parameters of rectangle stiffeners |
为了验证本文所建立的无限大光滑平板和单向加筋平板声振理论模型以及计算方法的有效性,先通过本文方法计算静止流体中单向加筋平板的远场声压级与Maxit的方法所给出的结果来对比,接着再与有限元法的计算结果进行对比。由于Maxit是通过离散傅里叶变换法建立的求解静止流场中周期加筋板振动响应和声压的理论方法,并与Mace所给出的结果进行了对比,且结果吻合的很好。因此,如果同样工况下本文方法和Maxit的方法所给出的结果一致或相差不大,就能证明本文方法合理有效。在理论模型验证过程中,平板和加强筋的材料都采用表 1中的钢,加强筋的截面参数如表 2工况1所示,其余参数按照上节介绍的来选取。图 4给出了本文方法和Maxit的方法来计算单向加筋平板在10 Hz~10 kHz频率范围内,作用点位置为(x0,y0)=(0,0)和(L/2,0)时的声压级曲线对比图。
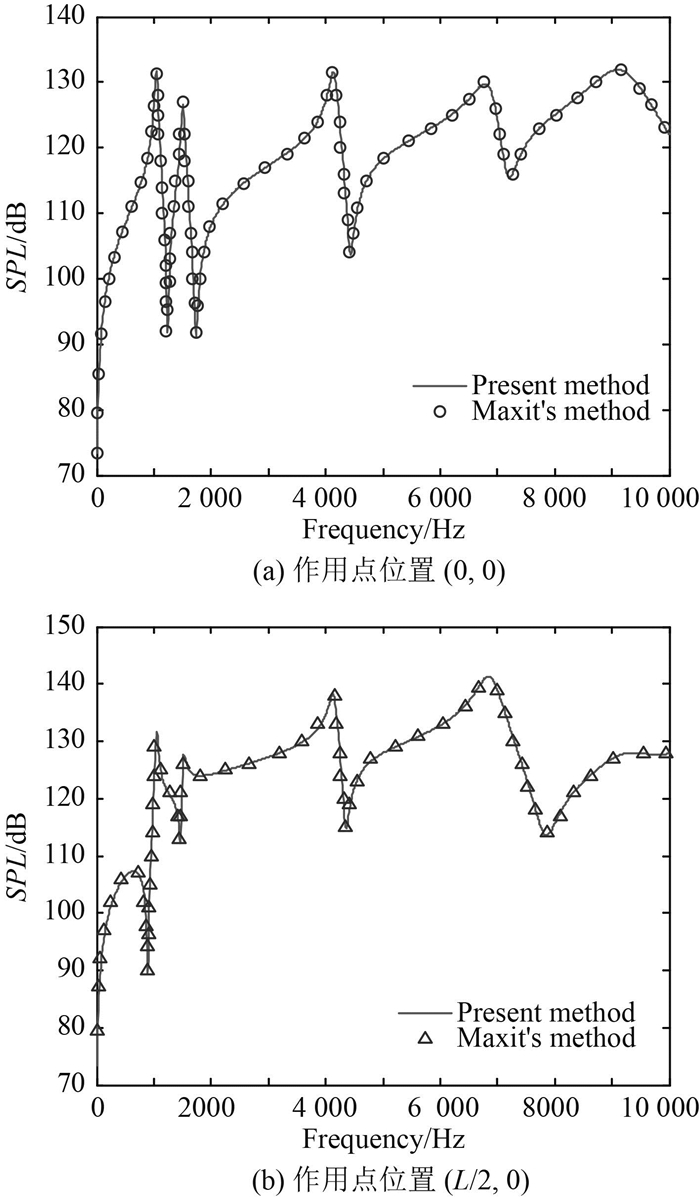
|
图 4 理论结果与Maxit理论结果的对比 Fig. 4 Comparison between present model predictions and Maxit's results for SPL |
由图 4可知,本文方法计算结果与Maxit方法所给出的计算结果在2个作用点位置处的SPL曲线完全吻合,这说明本文理论模型合理,计算方法是正确且精度高。
在将本文方法与有限元法进行对比时,结构的关键参数定义如下:平板厚度h=0.004 mm,加强筋间距L=0.156 m,加强筋为矩形截面,截面宽度为a=0.013 m,截面高度为b=0.038 m,作用点位置为(x0,y0)=(L/2,0),计算频率范围为100~3 000 Hz,有限元模型的尺寸为:5 m ×5 m。这样有限元模型中就包含31个周期单元,加强筋和平板都采用有限元软件ANSYS来建模,为了减少尺寸效应的影响本文将板和加强筋的材料损耗因子扩大10倍(即令η=0.2)。有限元模型的四角采用简支约束,其他参数与理论模型相同,进行谐响应分析。由此计算得到单向加筋平板声辐射的理论计算结果与有限元模拟结果如图 5所示。
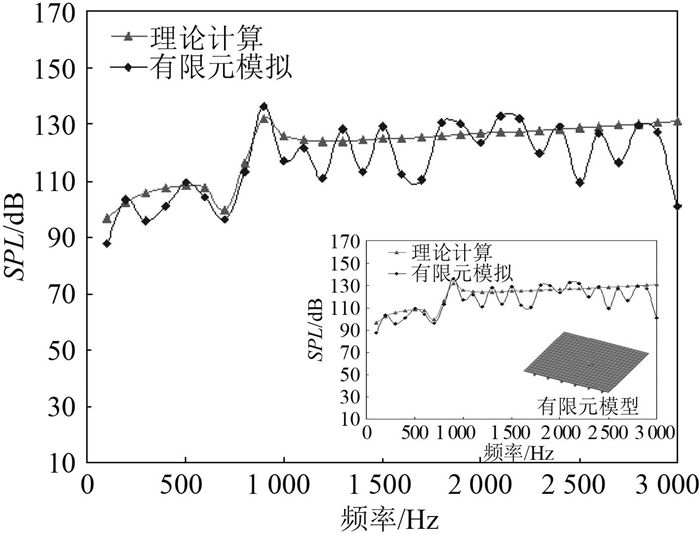
|
图 5 单向加筋平板声辐射理论计算结果与有限元模拟结果对比 Fig. 5 Comparison between present model predictions and FE results |
由图 5可知,由本文理论模型计算得到的单向加筋平板的远场辐射声压(SPL)曲线在频率分别等于700 Hz和900 Hz两个频点处出现了辐射波谷和波峰,在其他部分都是比较光滑的曲线。虽然由有限元法计算得到的SPL曲线随频率变化会波动,但是它基本上还是在理论计算曲线上下摆动,而且在700 Hz和900 Hz两个频点处同样出现了明显的辐射波谷和波峰。有限元模拟的SPL曲线出现波动的原因是因为采用有限大结构来模拟无限大结构时,平板弯曲波会在平板边缘处发生反射所造成的。由上可知无限大结构的理论计算结果能反映出实际有限大结构声辐射的整体变化趋势。由此可知,本文所建立的理论模型合理有效。
2.2.2 收敛性分析由于本文最后的计算方法通过将无限大线性代数方程组截断成有限大小来求解,因此后续进行数值研究的第1步是要确定级数求解的项数是多少才能使得所求结果收敛且满足精度要求(容差为0.01 dB)。同时,由收敛性知识可知[10],如果所求结果在某一“给定频率”下收敛,那么当频率低于该“给定频率”时其计算结果都收敛。
数值计算时,先假设单向加筋平板的材料为各向同性钢材料,加强筋截面参数如表 2工况1所示,单位力的作用点为(x0,y0)=(0,0),其他参数保持不变。图 6给出了不同频率f=0.5,1,10 kHz时,SPL值随项数变化的收敛性曲线。由于本文所研究的最高频率为10 kHz,因此以10 kHz为“给定频率”所确定的级数求和项数能使得所有低于10 kHz频率的计算结果都能达到精度要求。
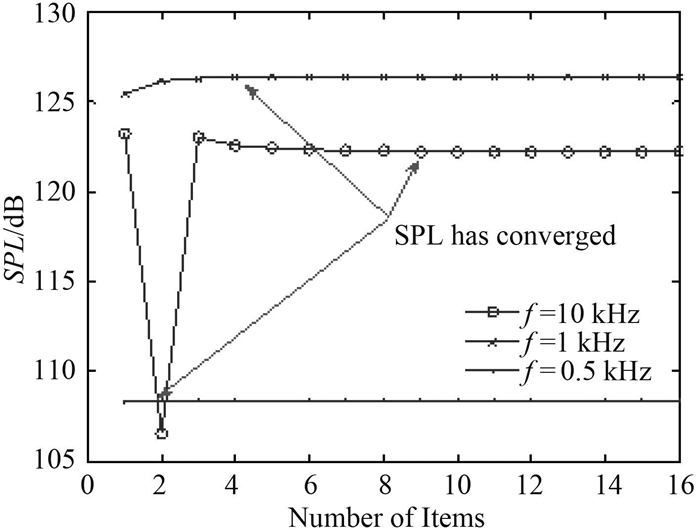
|
图 6 不同频率时单向加筋平板数值解收敛性分析图 Fig. 6 Convergence check of numerical solution for sound radiation from parallel stiffened plate with different frequencies |
由图 6可知,随着频率不断增加,SPL值达到0.01 dB精度要求所需的级数求和项数也在不断增加。其中,f=0.5,1,10 kHz时,为了保证结果收敛所需的项数分别为2,4,9项。由此可知,频率越高时结果收敛所需项数也越多。这与前面结论相同。因而,当k=9(M=2k+1=19)时,所有计算结果都能在f≤10 kHz时收敛且达到精度为0.01 dB的要求。
2.3 参数影响分析通过将本文方法与文献中的计算结果以及成熟的数值计算方法的对比,证明了本文理论模型与计算方法的正确性,同时,通过收敛性分析,确定了在本文所关注的频段内,无限大线性方程组数值截断计算结果收敛的所需截断项数。本节将运用上述理论模型和数值方法分析模型参数对单向加筋平板远场声辐射特性的影响规律。
2.3.1 加强筋的影响为了研究加强筋作用的影响,本节将比较静止流场中无限大平板和无限大单向加筋平板的远场辐射声压级曲线。数值计算时,假设平板和加强筋都钢,其材料属性见表 1。计算远场辐射声压级SPL(0≤f≤10 kHz)和远场指向性曲线(f=1 kHz,θ=45°)时,平板厚度取0.004 8 m,加强筋间距为0.156 m,坚加强筋截面参数取表 2中的工况1,载荷作用位置为(x0,y0)=(0,0)。图 8给出了静止流体中无限大光滑平板和单向加筋平板远场辐射声压级SPL的对比结果。
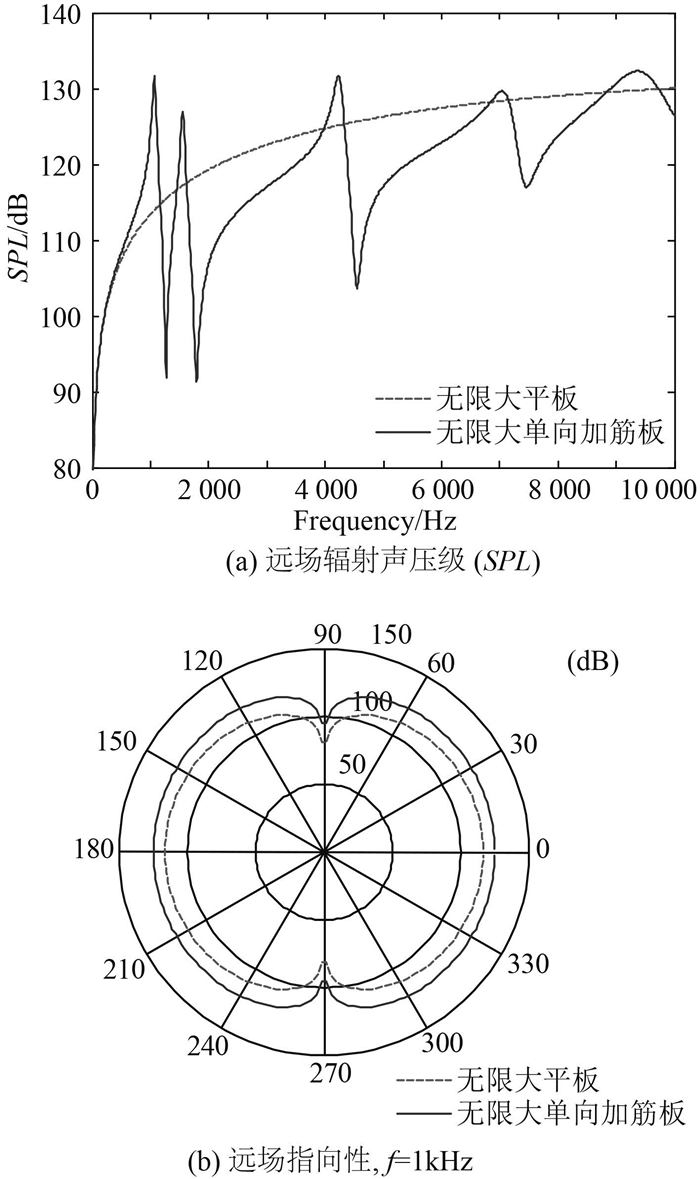
|
图 7 无限大平板和单向加筋平板声辐射的对比,作用点(0,0) Fig. 7 Comparison between infinite and parallel stiffened plate for sound radiation, when the point force located at (0, 0) |
|
图 8 不同马赫数Ma下光滑平板和单向加筋平板的SPL曲线 Fig. 8 SPL curves for bare and parallel stiffened plate with different Mach number |
观察图 7(a)发现,无限大光滑平板的SPL曲线是1条逐渐上升的光滑曲线;在较低频段,无限大单向加筋平板的SPL曲线与无限大光滑平板的SPL曲线,也是一段光滑曲线;随着频率不断增加,无限大单向加筋平板的SPL曲线会围绕着无限大光滑平板的光滑SPL曲线上下振荡,其SPL曲线多出了很多与最大和最小声辐射对应的波峰和波谷。这是由于与无限大光滑平板相比,无限大单向加筋平板中由于加强筋的存在使得其振动模态变得丰富。不过,二者的总体变化趋势还是保持一致。由图 7(b)可知,无限大光滑平板和单向加筋平板的远场指向性曲线相同,都对称于φ=90°这条轴线。只不过单向加筋平板的声压值要比无限大平板的声压值大,这可以从图 7(a)得到证明。
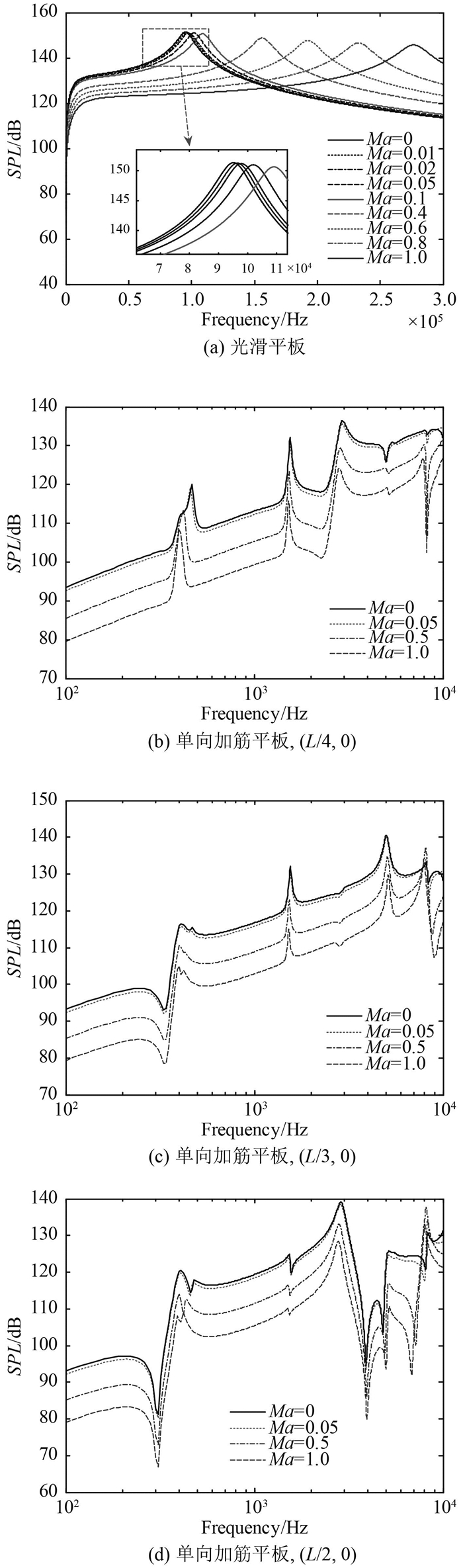
2.3.2 流体运动的影响图 8给出了来流入射角ε=45°时不同马赫数下无限大光滑平板和单向加筋平板的SPL曲线。计算光滑平板的SPL时,平板厚度不变,马赫数取0,0.01,0.02,0.05,0.1,0.4,0.6,0.8和1.0等9种不同情况。计算单向加筋平板的SPL时,作用点取(L/4,0),(L/3,0)和(L/2,0)等3种不同情况,每种情况下马赫数都取了4种不同情况。
但实际上舰艇在水中的运动速度都不会太大,因此它们的马赫数一般都比较小,若按35 kn来折算的话,马赫数才达到0.012。按照Ma=0.012来计算辐射声压与Ma=0时结果之间的误差不会超过0.3 dB。由于本文是做理论定性分析,所以这种误差是可以接受的。因此,为了研究方便本文接下来的研究中理论推导还是按照运动场结构的辐射特性来建模,但是实际数值计算时则按照静止流体来进行计算。
2.3.3 材料的影响图 9给出了材料对单向加筋平板远场辐射声压级(SPL)的影响规律。材料分别选取钢、铝和黄铜3种不同材料,其具体属性见表 1。在计算单向加筋平板的远场辐射声压级时,板厚取0.004 8 m,加强筋间距取0.2 m,加强筋界面参数取表 3中工况一,作用点位置分别取(0,0),(L/4,0),(L/3,0)和(L/2,0),计算频率为0.1~10 kHz。
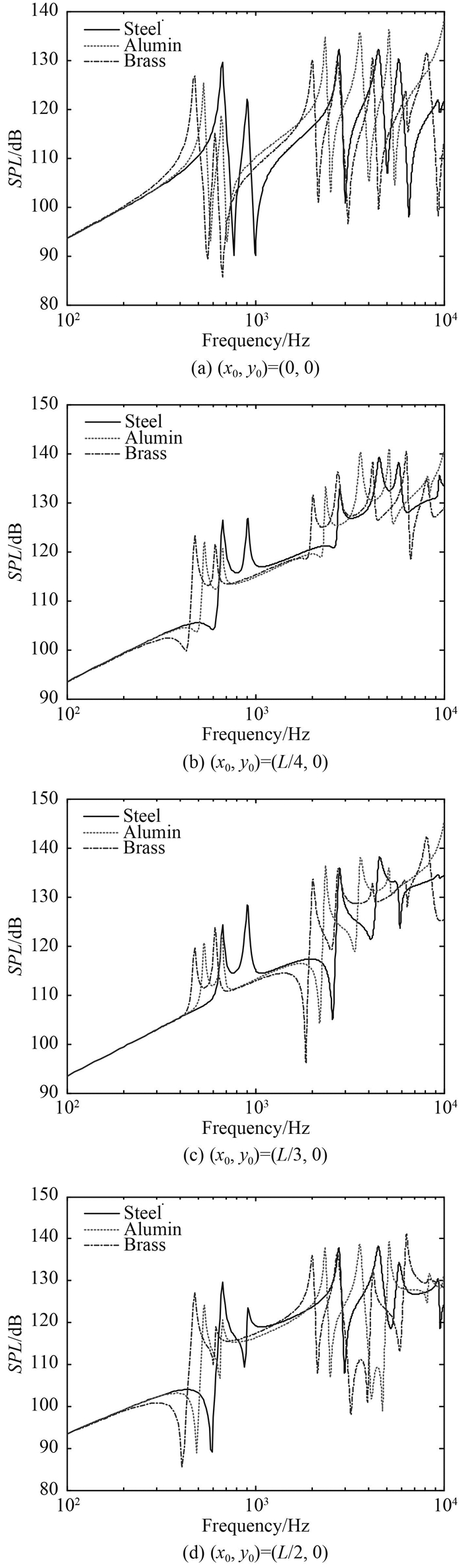
|
图 9 不同材料时单向加筋平板的SPL曲线 Fig. 9 SPL curve for parallel stiffened plate with different materials |
由图 9可知,材料对结构声辐射的影响也取决于材料的质量和刚度比。在低频段上,3种材料是SPL曲线基本上是重合在一起的,此时结构的声辐射是由流体负载的属性所决定的,这已经在上面的内容中被屡次提到;但是随着频率不断增加,材料对结构声辐射的影响也取决于材料的质量和刚度比。材料的质量和刚度比越大SPL值越小。由于钢的质量和刚度比最小,黄铜最大,所以材料为钢时的SPL曲线整体上要高于其他两种材料。
从图 9还可以看出,当材料分别取钢,铝和黄铜时,其对应的SPL曲线上所有的波峰和波谷都向低频推移,其中材料为钢时的SPL曲线上所有波峰波谷所对应的频率最大。这是因为辐射波峰和波谷取决于结构的固有频率,而固有频率则由材料的刚度与质量之比所决定。由表 1中材料的弹性模量和密度可知,钢的刚度与质量之比最大,铝次之,黄铜最小,所以对应的SPL曲线才会逐渐向低频偏移。为了方便研究,后续分析中加强筋和平板的材料都选钢。
2.3.4 平板厚度的影响图 10给出了4种不同作用点位置下,0.003 m,0.004 m和0.005 m等3种平板厚度下单向加筋平板的SPL曲线。
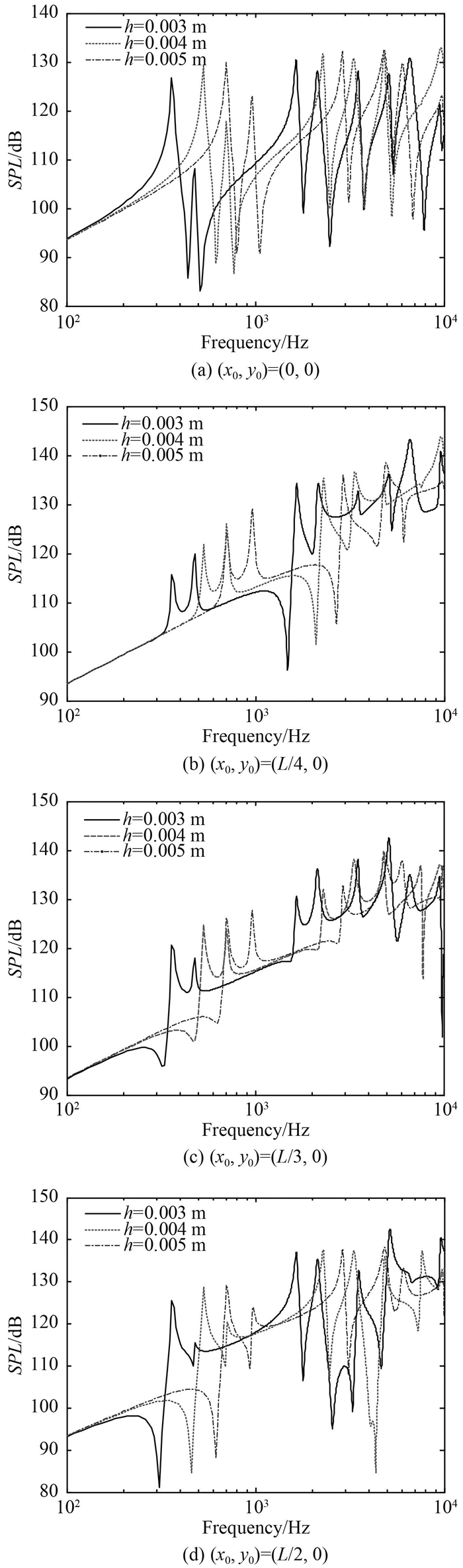
|
图 10 不同平板厚度下单向加筋平板的SPL曲线 Fig. 10 SPL curve for parallel stiffened plate with different plate thickness |
由图 10可知,平板厚度变化对单向加筋平板声辐射曲线的影响度非常明显。由图 10可知,3种不同平板厚度时结构的SPL曲线总体趋势一致,这是因为单向加筋平板结构具有高度相似的周期特性。不断增加平板厚度会使得SPL曲线上对应的辐射声压波峰和波谷逐渐向高频段推移,而SPL曲线的低频光滑段则会随着不断增加。这是由于平板厚度增加后会使得结构的固有频率增加,从而使得结构的SPL曲线会整体向高频方向移动。
2.3.5 加强筋间距的影响由于加强筋周期间距L是描述周期加筋平板结构周期特性的关键系统参数,所以加强筋间距L变化必然会对结构的声振耦合特性产生重要影响。本节将研究不断改变加强筋间距对单向加筋平板远场辐射声压的影响规律。在分析加强筋间距对单向加筋平板横远场辐射声压级的影响时,平板厚度取0.005 m,载荷作用位置分别取(0,0),(L/4,0),(L/3,0)和(L/2,0),加强筋截面参数取表 3中工况一,加强筋间距分别取0.15 m,0.20 m和0.25 m四种情况,计算频率为0.1~10 kHz,由此得到的远场辐射声压级如图 11所示。
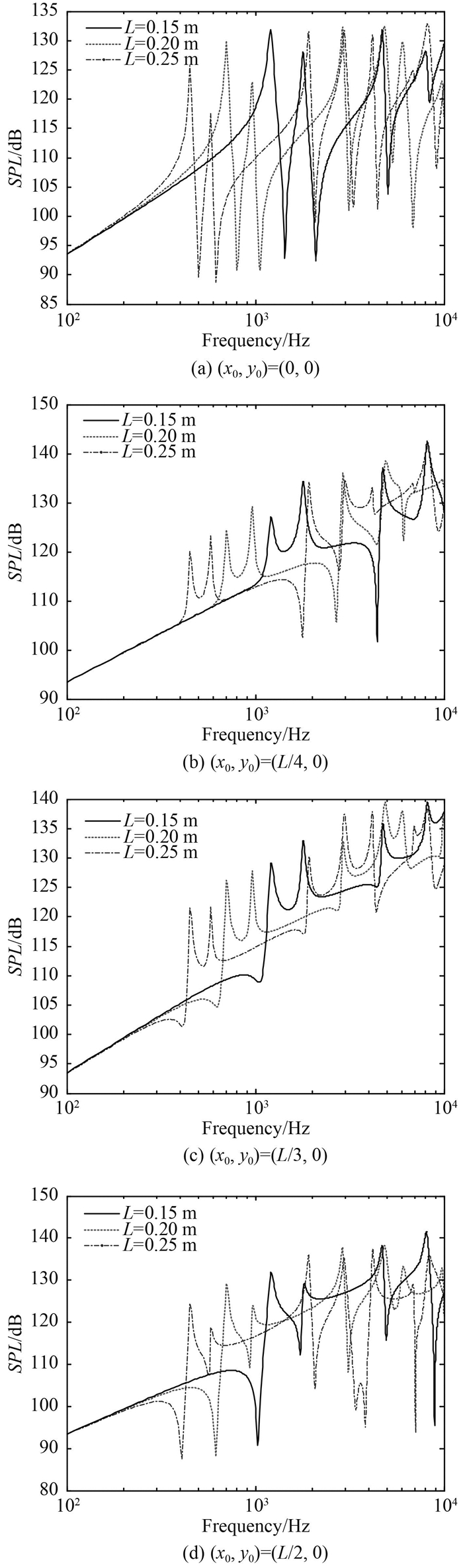
|
图 11 不同加强筋间距下单向加筋平板的SPL曲线 Fig. 11 SPL curves for parallel stiffened plate with different stiffener spacing |
由图 11可知,3条SPL曲线总体上的变化趋势还是能保持很好的一致性。在低频段,改变加强筋间距对结构声辐射的影响不大,3种不同强筋间距时的SPL曲线基本上重合;加强筋间距变化主要在中高频段显著影响结构的声辐射,这是因为此时平板弯曲波波长与结构加强筋间距在量值上相当。随着加强筋间距不断增加,结构SPL曲线上的波峰和波谷不断向低频方向移动。这是因为结构的固有频率随着加强筋间距不断增加而减少,因而SPL曲线上与结构固有频率所对应的波峰和波谷才会逐渐向低频推移。与改变平板厚度一样,通过合理选择加强筋间距可以设计出力学和声学性能最优的结构形式。
3 结语为了研究航行态舰艇结构声辐射特性,本文从舰艇结构中选取最简单的光滑平和单向加筋平板结构,开展初步理论分析和数值计算研究。本文分别从光滑平板和单向加筋平板的声振耦合方程,均匀流中的波动方程和边界条件出发,利用傅里叶变换法和泊松求和公式建立波数域中光滑平板单向加筋平板声振耦合理论模型;然后以单向加筋平板为例给出了截断求解理论模型的数值计算方法,并且通过与已有理论方法计算得到结果及有限元模型得到结果对比验证了本文方法的合理性和有效性。数值分析中详细讨论了系统参数对结构远场声辐射特性的影响规律,结论如下:
1)当流体运动时的马赫数(Ma) > 0.05时,由于其折射效应的影响可以降低结构的辐射声压。但是实际舰艇航行时的马赫数要远低于0.05,此时这种影响可以忽略。因此以静止流体来代替均匀流分析结构的声辐射特性不会造成太大误差。
2)材料对单向加筋平板的振动和声辐射有重要影响。通过数值分析可知,其声辐射曲线中低频段为刚度控制域,而高频段为质量控制域。
3)平板厚度对单向加筋平板声辐射特性影响显著。随着平板厚度增加会使得结构的固有频率增加,从而使得结构的SPL曲线会整体向高频方向移动,其低频平滑段增加。
4)改变加强筋间距影响非常明显。随着加强筋间距不断增加会使得结构的固有频率降低,使得结构的SPL曲线会向低频段偏移,而低频平滑段减少。
| [1] | LAULAGNET B. Sound radiation by a simply supported unbaffled plate[J]. The Journal of the Acoustical Society of America , 1998, 103 (5) :2451–2462. DOI: 10.1121/1.422765 |
| [2] | PARK J, MONGEAU L, SIEGMUND T. Influence of support properties on the sound radiated from the vibrations of rectangular plates[J]. Journal of Sound and Vibration , 2003, 264 (4) :775–794. DOI: 10.1016/S0022-460X(02)01215-4 |
| [3] | BERRY A, GUYADER J L, NICOLAS J. A general formulation for the sound radiation from rectangular, baffled plates with arbitrary boundary conditions[J]. The Journal of the Acoustical Society of America , 1990, 88 (6) :2792–2802. DOI: 10.1121/1.399682 |
| [4] | MEAD D J. Free wave propagation in periodically supported, infinite beams[J]. Journal of Sound and Vibration , 1970, 11 (2) :181–197. DOI: 10.1016/S0022-460X(70)80062-1 |
| [5] | MEAD D J. Vibration response and wave propagation in periodic structures[J]. Journal of Engineering for Industry , 1971, 93 (3) :783–792. DOI: 10.1115/1.3428014 |
| [6] | MEAD D J, PUJARA K K. Space-harmonic analysis of periodically supported beams:Response to convected random loading[J]. Journal of Sound and Vibration , 1971, 14 (4) :525–541. DOI: 10.1016/0022-460X(71)90579-7 |
| [7] | MEAD D M. Wave propagation in continuous periodic structures:Research contributions from Southampton, 1964-1995[J]. Journal of Sound and Vibration , 1996, 190 (3) :495–524. DOI: 10.1006/jsvi.1996.0076 |
| [8] | MEAD D J, MALLIK A K. An approximate theory for the sound radiated from a periodic line-supported plate[J]. Journal of Sound and Vibration , 1978, 61 (3) :315–326. DOI: 10.1016/0022-460X(78)90383-8 |
| [9] | MATHUR G P, TRAN B N. BOLTON J S, et al. Sound transmission through stiffened double-panel structures lined with elastic porous materials[C]//Proceedings of the 14th DGLR/AIAA Aero-Acoustics Conference. Aachen, Germany:AIAA, 1992:102-105. |
| [10] | LEE J H, KIM J. Analysis of sound transmission through periodically stiffened panels by space-harmonic expansion method[J]. Journal of Sound and Vibration , 2002, 251 (2) :349–366. DOI: 10.1006/jsvi.2001.4008 |
| [11] | RUMERMAN M L. Vibration and wave propagation in ribbed plates[J]. The Journal of the Acoustical Society of America , 1975, 57 (2) :370–373. DOI: 10.1121/1.380450 |
| [12] | MACE B R. Periodically stiffened fluid-loaded plates. Ⅰ:Response to convected harmonic pressure and free wave propagation[J]. Journal of Sound and Vibration , 1980, 73 (4) :473–486. DOI: 10.1016/0022-460X(80)90662-8 |
| [13] | MACE B R. Periodically stiffened fluid-loaded plates. Ⅱ:Response to line and point forces[J]. Journal of Sound and Vibration , 1980, 73 (4) :487–504. DOI: 10.1016/0022-460X(80)90663-X |
| [14] | MACE B R. Sound radiation from a plate reinforced by two sets of parallel stiffeners[J]. Journal of Sound and Vibration , 1980, 71 (3) :435–441. DOI: 10.1016/0022-460X(80)90425-3 |
| [15] | MACE B R. The vibration of plates on two-dimensionally periodic point supports[J]. Journal of Sound and Vibration , 1996, 192 (3) :629–643. DOI: 10.1006/jsvi.1996.0211 |
| [16] | MACE B R. Sound radiation from fluid loaded orthogonally stiffened plates[J]. Journal of Sound and Vibration , 1981, 79 (3) :439–452. DOI: 10.1016/0022-460X(81)90321-7 |
| [17] | MACE B R. Periodically stiffened fluid-loaded plates. Ⅱ:Response to line and point forces[J]. Journal of Sound and Vibration , 1980, 73 (4) :487–504. DOI: 10.1016/0022-460X(80)90663-X |
| [18] | MAXIT L. Wavenumber space and physical space responses of a periodically ribbed plate to a point drive:A discrete approach[J]. Applied Acoustics , 2009, 70 (4) :563–578. DOI: 10.1016/j.apacoust.2008.06.012 |
| [19] | MAIDANIK G. Surface-Impedance nonuniformities as wave-vector convertors[J]. The Journal of the Acoustical Society of America , 1969, 46 (5A) :1062–1073. DOI: 10.1121/1.1911822 |
| [20] | LYON R H. Sound radiation from a beam attached to a plate[J]. The Journal of the Acoustical Society of America , 1962, 34 (9A) :1265–1268. DOI: 10.1121/1.1918317 |
| [21] | NAYAK P R. Line admittance of infinite isotropic fluid-loaded plates[J]. The Journal of the Acoustical Society of America , 1970, 47 (1B) :191–201. DOI: 10.1121/1.1911462 |
| [22] | ROMANOV V N. Radiation of sound by an infinite plate with reinforcing beams[J]. Soviet Physics:Acoustics , 1971, 17 (1) :92–96. |
| [23] | EVSEEV V N. Sound radiation from an infinite plate with periodic inhomogeneities[J]. Soviet Physics:Acoustics , 1973, 19 (3) :226–229. |
| [24] | FRAMPTON K D. Radiation efficiency of convected fluid-loaded plates[J]. The Journal of the Acoustical Society of America , 2003, 113 (5) :2663–2673. DOI: 10.1121/1.1559173 |
 2016, Vol. 38
2016, Vol. 38
