0 引言

三体船作为一种新型的高性能船舶，拥有优良的耐波性以及快速性^[1]，其在军民舰船中拥有广阔的应用前景，世界各国也愈加重视对其阻力性能的研究^[2]。三体船一般由1个中体和1对侧体组成，侧体分布在中体两侧，一般侧体的排水量不超过总排水量的10%^[3]。三体船的中体一般都设计成瘦长型，以减小其兴波阻力，但船体的细长会导致稳性的不足，采用安装在三体船两侧的侧体恰恰弥补了其稳性不足的缺陷。同时，对于军用船舶而言，侧体一般为三体船的关键部位的防护^[4]，即便侧体收到损伤，浮力的损失也不大，提高了舰船的生存能力。过小的侧体排水量比会导致三体船稳性的不足，不利于甲板布置等；过大的侧体则会直接增大三体船的湿表面积^[5]，对三体船的阻力性能不利。选择合适的三体船侧体排水量比是三体船设计工作中的重要组成部分。

本文针对一艘高速三体船设计了5种侧体排水量比方案，基于时均化的Navier-Stokes方程的方法，采用VOF法捕捉自由液面，数值模拟不同侧体排水量比下的总阻力以及摩擦阻力，计算相应的剩余阻力系数，分析各方案下自由面波形变化，对侧体排水量比对兴波阻力的影响进行了探讨，并将计算结果与试验结果进行比较，验证CFD计算的可靠性。

1 CFD数值计算 1.1 基本方程及湍流模型

对于空间固定的无限小流体元模型，假设流体不可压，则流场的连续性方程为：

$ \frac{\partial {{u}_{i}}}{\partial {{x}_{i}}}=0, $

(1)

动量守恒方程为：

$ \rho \left[\frac{\partial \overline{{{u}_{i}}}}{\partial t}+\frac{\partial(\overline{{{u}_{i}}{{u}_{j}}})}{\partial {{x}_{j}}} \right]=-\frac{\partial \bar{p}}{\partial {{x}_{i}}}+\mu {{\nabla }^{2}}{{u}_{i}}+\frac{\partial }{\partial {{x}_{j}}}(-\rho \overline{{{u}_{{{i}'}}}{{u}_{{{j}'}}}})\text{.} $

(2)

式中：$\overline {{u_i}} $，$\overline {{u_j}} $为速度分量时均值（i，j=1，2，3），$\bar p$为压力时均值，ρ为流体密度，μ为流体的动力粘性系数，$\rho \overline {u_i'u_j'} $为雷诺应力项。由于湍流运动的方程组引入的雷诺应力项为新的未知量，需引入新的湍流模型，将湍流的脉动值与时均值联系起来，从而使方程组封闭。

工程中比较常用的湍流模型为涡粘模型^[6]，采用引入湍流粘度μ_t，然后把湍流应力表示成湍流粘度的函数。涡粘模型包含零方程模型、一方程模型、二方程模型。其中，标准k-ε模型为目前使用最为广泛的二方程模型^[7]，但由于标准k-ε模型由于湍流粘度μ_t是定义为各向同性的标量，在应用于带强旋流及弯曲壁面流动时，会产生一定的失真，因此本文采用改进的Realizablek-ε模型，认为湍流粘度计算式中的系数C_μ不应是常数，而应与应变率联系起来。该模型的湍动能k和耗散率ε的输送方程分别为：

$ \frac{\partial \left(\rho k \right)}{\partial t}+\frac{\partial \left(\rho k{{u}_{i}} \right)}{\partial {{x}_{i}}}=\frac{\partial }{\partial {{x}_{j}}}\left[\left(\mu+\frac{{{\mu }_{t}}}{{{\sigma }_{k}}} \right)\frac{\partial k}{\partial {{x}_{j}}} \right]+{{G}_{k}}-\rho \varepsilon \text{, } $

(3)

$ \frac{\partial \left(\rho \varepsilon \right)}{\partial t}+\frac{\partial \left(\rho \varepsilon {{u}_{i}} \right)}{\partial {{x}_{i}}}=\frac{\partial }{\partial {{x}_{j}}}\left[\left(\mu+\frac{{{\mu }_{t}}}{{{\sigma }_{\varepsilon }}} \right)\frac{\partial \varepsilon }{\partial {{x}_{j}}} \right]+\rho {{C}_{1}}E\varepsilon -\rho {{C}_{2}}\frac{{{\varepsilon }^{2}}}{k+\sqrt{\nu \varepsilon }}\text{.} $

(4)

其中，S_k和S_ε 为指定的源项，σ_k =1.0，σ_ε =1.2， ${C_1}={\rm{max}}\left({0.43, \dfrac{\eta }{{5+\eta }}} \right)$ ， $\eta={\left({2{E_{ij}} \cdot {E_{ij}}} \right)^{1/2}}\dfrac{k}{\varepsilon }$ ， ${E_{{\rm{ij}}}}=\dfrac{1}{2}\left({\dfrac{{\partial {u_i}}}{{\partial {x_j}}}+\dfrac{{\partial {u_j}}}{{\partial {x_i}}}} \right)$ ，C₂=1.9。

湍流粘度不再认为是常数，而是： ${\mu _t}=\rho {C_\mu }\dfrac{{{k^2}}}{\varepsilon }$ ，

系数C_μ为

$ {{C}_{\mu }}=\frac{1}{{{A}_{0}}+{{A}_{S}}{{U}^{\left(* \right)}}\frac{k}{\varepsilon }}\text{.} $

(5)

其中： ${A_S} \!=\! \sqrt 6 {\rm{cos}}\varphi $ ， $\varphi \!=\! \dfrac{1}{3}{\rm{arccos}}\left({\sqrt 6 W} \right)$ ， $W \!=\! \dfrac{{{E_{{\rm{ij}}}}{E_{jk}}{E_{ki}}}}{{\left({{E_{ij}}{E_{ij}}} \right)}}$ ， ${U^{\left(* \right)}}=\sqrt {{E_{ij}}{E_{ij}}+{{\overline \varOmega }_{ij}}{{\overline \varOmega }_{ij}}}$ 。

${\overline \varOmega _{{\rm{ij}}}}$为角速度为ω_k的参考系中观察到的时均转动速率张量：

$ {{{\bar{\Omega }}}_{ij}}={{\Omega }_{ij}}-2{{\varepsilon }_{ijk}}{{\omega }_{k}}\text{, } $

(6)

$ {{\Omega }_{\text{ij}}}={{{\bar{\Omega }}}_{ij}}-{{\varepsilon }_{ijk}}{{\omega }_{k}}\text{, } $

(7)

其他参数：A₀=4.0，C_ε2=1.9，σ_k =1.0，σ_ε =1.2。

1.2 自由液面处理

采用界面捕捉法中的VOF法^[8]，其思想为通过在网格上定义流体体积因子α，其值为该网格内流体域网格的体积比值。定义函数：

$ \alpha(\vec{x}, t)=\left\{ \begin{array}{*{35}{l}} 1, \vec{x}\in {{V}_{1}}\text{;} \\ 0, \vec{x}\in {{V}_{2}}\text{.} \\ \end{array} \right. $

(8)

对于2种不同的流体介质组成的流场，$\alpha(\overrightarrow x, t)$满足

$ \frac{\partial \alpha }{\partial t}+\vec{U}\cdot \nabla \alpha=0. $

(9)

其中 $\overrightarrow U $ 为流体的速度场，定义VOF函数C_ijk 为 $\alpha(\overrightarrow x, t)$ 在网格单元上的积分除以单元体积，即

$ {{C}_{ijk}}=\frac{1}{\Delta {{V}_{ijk}}}\int_{{{I}_{ijk}}}{\alpha(\vec{x}, t)\text{d}\vec{v}}\text{, } $

(10)

$ \text{且}{{C}_{ijk}}\text{满足}\frac{\partial C}{\partial t}+\vec{U}\cdot \nabla C=0. $

(11)

当C=1时，网格内充满流体1；当C=2时，网格内充满流体2；当C值介于0~1之间，则网格内包含流体1和流体2，即存在交界面。通过求出每个网格中的C值，得出网格单元上的流体填充情况，计算自由面的扭曲倾斜率，进而生成比较精确的自由面。

2 数值计算 2.1 计算模型

计算模型为1艘高速三体船船型，该模型由1个中体和1对侧体组成，左右侧体相对中体的纵中剖线对称布置，其大小、形状完全相同，该三体船的中体和侧体均为大长宽比的圆舭船型，其中，中体为带球艏的细长体方尾圆舭船型；侧体为超细长体方尾圆舭船型。在工程较为实用的侧体排水量比的范围内，选择5个典型的侧体排水量比，三体船的侧体排水量比的变化是通过调整三体船的中体和侧体的垂向相对位置而实现，在调整过程中保证三体船的总排水量不变。模型主尺度参见表 1和表 2。其中，Δs/Δ为侧体排水量占总排水量百分比，L为设计水线长，B为设计水线宽，d为设计吃水，Δ为排水量，b为侧体相对于中体的横向相对位置。所选取的5个排水体积比三体船模型的侧体布局均一致，即纵向位置侧体与中体的尾封板对齐，横向位置上侧体相对于中体的中纵剖面距离都为0.55 m。三体船计算模型如图 1所示。

2.2 网格划分

网格生成是CFD计算的基础^[9]，建立高质量的计算网格对CFD计算精度和计算效率有重要影响^[10]。由于三体船表面构型复杂，使用更具灵活性的目前使用更为广泛的非结构化混合网格进行网格划分。采用商业软件star-ccm的自动生成网格技术，采用对三体船表面进行网格重构生成高质量面网格，体网格则采用和面网格相接合的棱柱层（prism）网格和切割体（trim）网格。

流体计算域采用长方体型，入流口距离船首为1.5倍船长，出流口距离船尾3倍船长，流体域顶部距离船体底部为1倍船长，流体域底部距离船体底部为1.5倍船长。针对三体船中体和侧体之间采用加密区以捕捉之间的兴波干扰，对开尔文波系、尾流区域均进行了三层网格过渡加密，最终生成网格数量为1.26×10⁶。

2.3 边界条件

计算域入流口设置为速度入口，来流速度沿x轴向，湍流强度取常数；出流口设置为压力出口；顶部、底部和侧壁设置为速度入口，条件同入流口；船中纵剖面相切边界面设置对称面；船体为固壁无滑移条件。

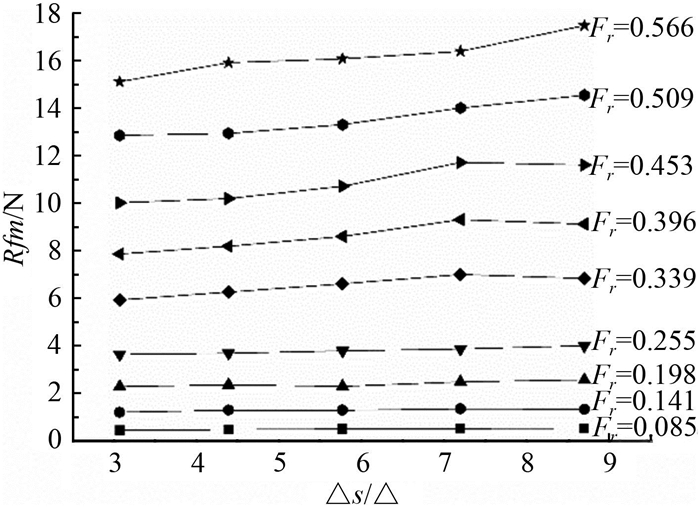
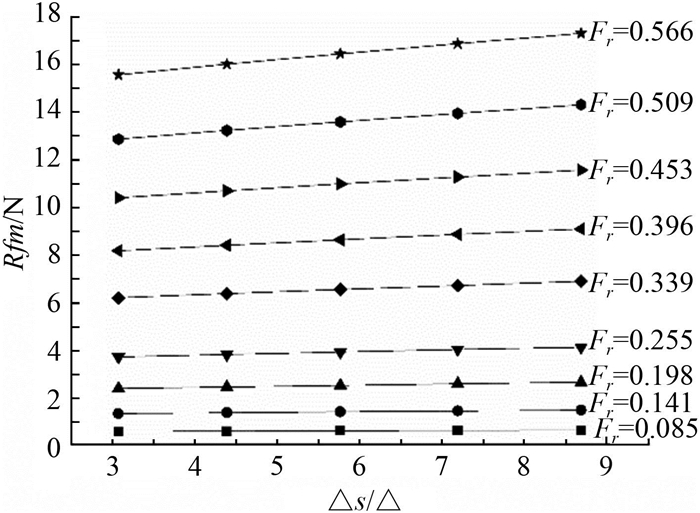
2.4 计算结果及分析

本文主要研究不同的侧体排水量比对三体船阻力性能的影响，针对5种侧体排水量比设计方案，对每种布局的三体船于傅汝德数F_r为0.085，0.141，0.198，0.255，0.339，0.396，0.453，0.509，0.566时分别进行了计算。一般计算剩余阻力系数，首先是对摩擦阻力进行计算，通常采用傅汝德方法（二因次法）计算，由于三体船的中、侧体设计水线长不一样，同样速度下各自的雷诺数不同，所以在计算摩擦阻力R_f时将中体与侧体分开，分别计算其雷诺数、摩擦阻力系数C_f并根据测得的中、侧体湿表面积计算各自的摩擦阻力，最后将中侧体的摩擦阻力值相加得到总摩擦阻力Rfm；另外一种方法就是通过求解RANSE方程，将数值计算求解得到的船身网格各节点处的应力，对船体水下表面进行积分，得到船体的总摩擦阻力。基于RANSE方法计算得到的摩擦阻力结果如图 3所示；按照二因次方法计算得到的摩擦阻力结果如图 4所示。

由上述结果可以看出，RANSE方法计算的摩擦阻力与二因次方法计算结果相比，在航速较低时，二者计算结果较为接近，当航速较高时，二者计算结果呈现较大偏差。分析原因，三体船航速较低时，航行姿态变化小，船体湿表面积变化不大，基本与正浮状态时相同，而傅汝德方法计算摩擦阻力所采用的为恒定的正浮状态时船体湿表面积，因而相差不大；当三体船处于高航速时，航行姿态发生较大变化，由于升沉、纵倾以及兴波的影响，三体船总湿表面积发生较大变化，摩擦阻力也随之而变。

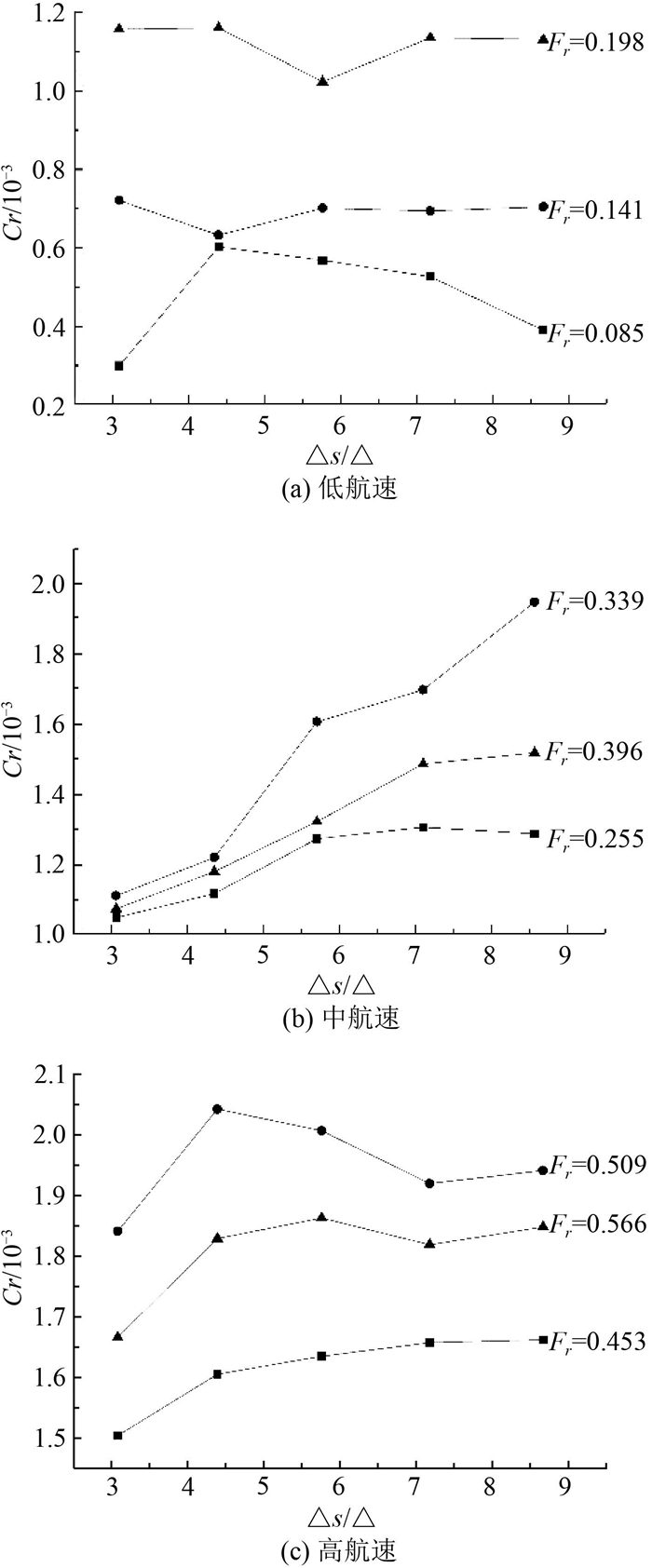
一般来讲，船舶的剩余阻力系数曲线一定程度上可反映出其兴波阻力的特点，由计算结果得到三体船剩余阻力系数曲线分析，进而对三体船的兴波阻力特征进行分析。由计算值得到的剩余阻力系数值绘制曲线如图 5所示。

由上述结果可见，侧体排水量对三体船的兴波阻力有一定的影响，同时这种影响还跟三体船的航速有关。在低航速段（F_r < 0.198），侧体排水量的变化对三体船剩余阻力影响不大，剩余阻力变化曲线呈现出相对平稳的状态；在中间航速段（0.255 < F_r < 0.396），同航速下，侧体排水量比较小的三体船布局具有较小的剩余阻力；在高航速段（F_r > 0.453），三体船的剩余阻力在侧体排水量比为4%~5%之间出现峰值，再增大侧体的排水体积比对三体船的剩余阻力影响不大。分析原因，航速较低时，三体船兴波较小，三体船总阻力中兴波阻力的比重较小，侧体排水量比变化对兴波阻力影响较小；当航速增加时，三体船兴波逐渐明显，波形之间干扰叠加作用愈加强烈，侧体排水量比较小的三体船的侧体兴波越小，与中体的兴波叠加干扰作用也就越小。当三体船处于高航速区时，三体船侧体兴波会随着排水体积比增大而增大，但侧体排水量比增大到一定程度时，三体船侧体兴波变化将不再明显。

为了较为直观地分析阻力变化情况，绘制了在F_r 为0.339时的5个侧体排水量比的三体船兴波波高云图，如图 6所示。

由以上自由液面波高图可知，数值模拟能较好地模拟出三体船片体之间的强烈的兴波干扰。在一定航速范围内，改变三体船的侧体排水量比对侧体的兴波影响较为显著，当三体船侧体排水量比为3.08%时，侧体的兴波最小，与中体产生的兴波干扰也最小，其后方的尾波波峰波谷范围也较小，兴波阻力也较小；逐渐增大三体船的侧体排水量比（8.67%内），侧体的兴波逐渐增大，与中体产生的兴波干扰作用也愈加强烈，分析原因，较小的侧体排水量比导致侧体的水下形状也较小，对水面的扰动作用也就越小；当增大侧体排水量比时，侧体的水下形状也随之增大，产生的兴波亦较大。由图可见，在侧体排水体积在3.08%~8.67%范围内变化时，中体的首部及尾部的兴波几乎没有变化，分析原因，三体船侧体排水量比在小范围内变化时，中体的排水量以及水下形状等变化不大，其兴波等变化亦不明显。

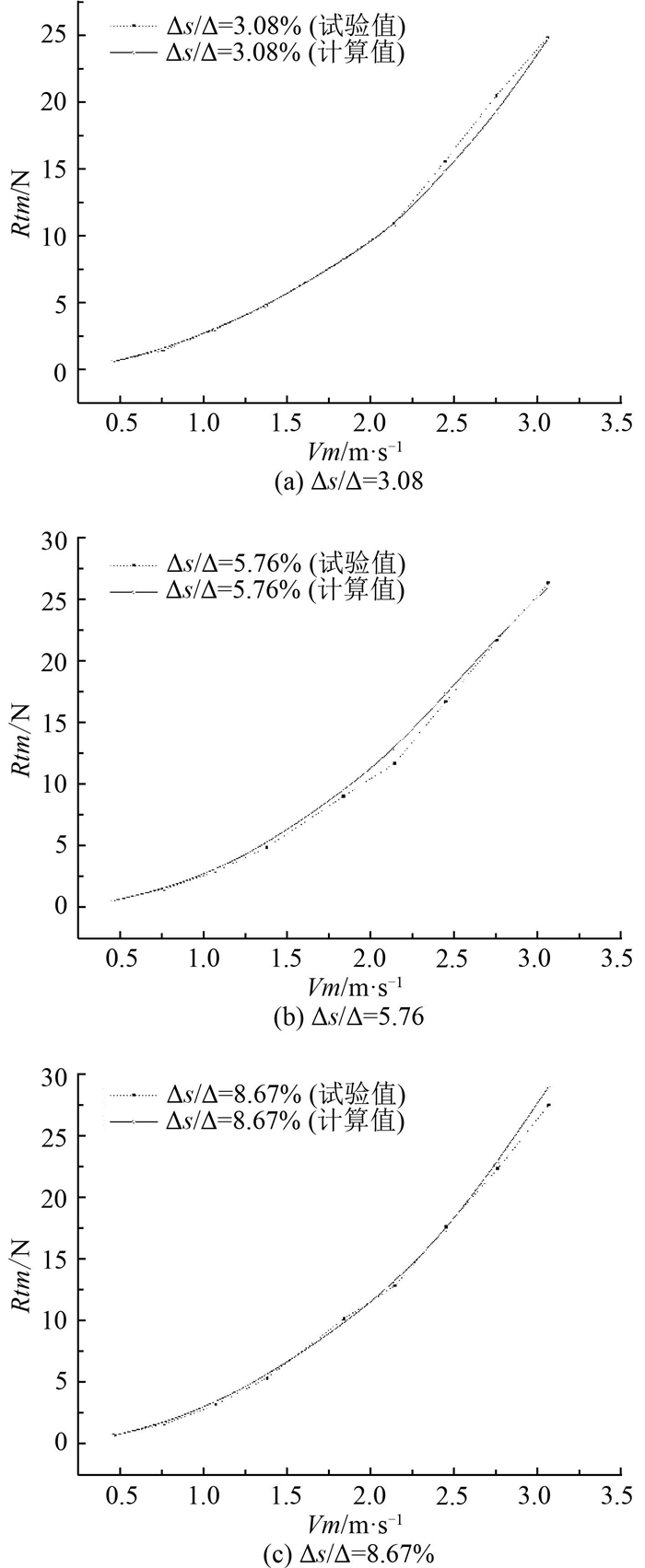
3 模型试验结果对比分析

为对数值计算结果的准确性进行验证，将三体船阻力计算结果与模型试验结果进行对比，如图 7所示。

从计算结果与实验结果的对比上可以看出，计算值与试验值吻合良好，表明计算结果具有较高的准确性，可以作为研究三体船阻力性能的一种方法。对于3种侧体排水量比模型，在中低速段时（F_r < 0.255），阻力的数值计算值与模型试验值很接近，误差在2%以内；在高速段（F_r > 0.339）时，阻力的数值计算值相对于模型试验值误差较大一些，平均约4%左右。原因可能是在高速运动时，三体船的航行姿态会发生变化，以及船首的破波和飞溅等现象，通过数值计算难以模拟；此外，在数值计算过程中会产生截断误差，由于网格数量较大，截断误差在高速时产生一定的积累。

4 结语

本文基于RANSE方法，对5种侧体排水量比的三体船布局进行阻力性能进行了计算及分析，探讨了主侧体间的兴波干扰特征，并与船模试验结果对比，得到结论如下：

1）三体船的阻力性能不仅与侧体的排水量比有关，同时还与航速密切相关，当F_r < 0.198时，由于兴波阻力占总阻力的比例不大，侧体的排水量变化对三体船的阻力性能影响不大。当F_r > 0.255时，侧体排水量比在3.08%左右的三体船兴波干扰较小，阻力性能亦较优。

2）侧体排水量比的变化对三体船侧体兴波影响较大，对三体船中体兴波影响较小。侧体排水量比的变化致使三体船侧体水下形状的变化，较小的侧体水下形状形成的兴波也较小。

3）当F_r > 0.453时，侧体排水量比超过4.39%后，再在一定范围内（小于8.67%）增大侧体排水量比，其兴波阻力变化不大，湿表面积的增大导致的摩擦阻力的上升为影响三体船阻力性能的主要因素。

本文就三体船侧体排水量变化对三体船阻力性能的影响进行了数值模拟研究，从计算结果来看，较小的侧体排水量比的三体船阻力性能更好，但三体船侧体排水量比的设计还需要结合稳定以及船体布置等进行综合考虑。本文仅进行了侧体排水量比变化对三体船阻力性能的影响，暂未考虑侧体布局位置及浮心纵向位置等因素对三体船阻力的影响，对此有待深入研究。