舰船雷达散射截面(RCS)是度量舰船对照射电磁波散射能力的一个物理量,它与舰船的几何形状物理参数、入射雷达波参数和舰船相对于雷达姿态角有关。水面舰船外形结构复杂,在掠海水平方向回波是舰船众多散射源和多路径综合的结果,其舷向、姿态变化和海面波动都将引起散射特性的变化。为保障岸基雷达设备测试舰船 RCS 的精度,需要规范舰船 RCS 岸基测试和处理方法,测试舰船各种状态下 RCS 特性及其参数间的关系,用统计方法说明其散射特性规律,以满足舰船设计、武器装备论证、试验鉴定等对舰船 RCS 应用需求。
1 雷达散射截面定义雷达目标散射截面(RCS)有基于电磁散射理论和雷达测试 2 种观点,两者的基本概念统一。
1.1 电磁散射理论定义雷达散射截面定义为单位立体角内目标朝接收方向散射功率与从给定方向入射于该目标平面波功率密度之比的
| $ \sigma = 4\pi \mathop {\lim }\limits_{R \to \infty } {{{R}}^2}\frac{{{{\left| {{{{E}}^s}} \right|}^2}}}{{{{\left| {{{{E}}^i}} \right|}^2}}} = 4\pi \mathop {\lim }\limits_{R \to \infty } {{{R}}^2}\frac{{{{\left| {{{{H}}^s}} \right|}^2}}}{{{{\left| {{{{H}}^i}} \right|}^2}}}{\text{。}} $ | (1) |
式中:Ei 和Hi 分别为入射雷达波在目标处的电磁场强度;Es 和Hs 为目标散射波在雷达处的电磁场强度,R 为雷达天线到目标的距离。
1.2 雷达测试理论定义雷达测试目标雷达散射截面,其电磁波传播途径由发射机、发射天线到目标、目标到接收天线、接收机等几部分组成。由雷达方程可知,接收功率的表达式为:
| $ \begin{aligned} {{{P}}_r} = & \frac{{{{{P}}_t}{{{G}}_t}}}{{{{{L}}_t}}} \cdot \frac{1}{{4\pi {{R}}_t^2{{{L}}_{mt}}}} \cdot \sigma \cdot \frac{1}{{4\pi {{R}}_r^2{{{L}}_{mr}}}} \cdot \frac{{{{{G}}_r}{\lambda ^2}}}{{4\pi {{{L}}_r}}}\\ & \Rightarrow (\text{发射}) \cdot (\text{传播}) \cdot (\text{目标}) \cdot (\text{传播}) \cdot (\text{接收}){\text{。}} \end{aligned} $ | (2) |
式中:Pr 为接收机输入端功率,W;Gr 和Gt 分别为接收天线与发射天线的增益;Lt 和Lmt 分别为发射机内馈线与发射天线到目标传播途径的损耗;Lr 和Lmr分别为接收机内馈线与目标到接收天线传播途径的损耗;σ为目标散射截面,m2;Rt 和Rr分别为发射天线到目标与目标到天线的距离,m。当是单站(收、发同一地点)时,Rt =Rr;λ 为雷达工作波长。
当忽略各种损耗,即Lt,Lmt,Lr,Lmr 均为 1 时,令
| $ \sigma = 4\pi \cdot \frac{{{{{P}}_r}}}{{{{\rm{A}}_r}/{{R}}_r^2}} \cdot \frac{1}{{\frac{{{{{P}}_t}{{{G}}_t}}}{{4\pi {{R}}_t^2}}}}{\text{。}} $ | (3) |
从式(3)中可看出,雷达散射截面等于接收天线所张立体角内的散射功率除以目标处照射功率密度的
根据雷达方程,测试舰船雷达散射截面通常采用相对比较法,公式为:
| $ \begin{aligned} \sigma = & \left( {\frac{{{{{P}}_{ts}}}}{{{{{P}}_t}}}} \right)\left( {\frac{{{{{P}}_r}}}{{{{{P}}_{rs}}}}} \right){\left( {\frac{{{G}}}{{{{{G}}_s}}}} \right)^2}{\left( {\frac{\lambda }{{{\lambda _s}}}} \right)^2}{\left( {\frac{{{R}}}{{{{{R}}_s}}}} \right)^4} \times \\ & {\left( {\frac{{{{{L}}_m}}}{{{{{L}}_{ms}}}}} \right)^2}\left( {\frac{{{{{L}}_t}}}{{{{{L}}_{ts}}}}} \right)\left( {\frac{{{{{L}}_r}}}{{{{{L}}_{rs}}}}} \right)\left( {\frac{{{{{L}}_p}}}{{{{{L}}_{ps}}}}} \right){\sigma _s}{\text{。}} \end{aligned} $ | (4) |
式中:σ 为目标雷达散射截面,m2;Pts 为测试标准体时雷达发射功率,W;Pt 为测试目标时雷达发射功率,W;Pr 为测试目标时接收目标回波功率,W;Prs 为测试标准体时接收标准体回波功率,W;G 和Gs 为测试目标、标准体时雷达天线增益;λ 和λs 为测试目标、标准体时雷达工作波长,m;R 和Rs 为目标、标准体到天线的距离,m;Lm 和Lms 为雷达到目标与标准体之间的大气传输损耗;Lt 和Lts 为发射机内馈线与发射天线到目标传播途径的损耗;Lr 和Lrs 为接收机内馈线与目标到接收天线传播途径的损耗;Lr 和Lrs 为测试目标与标准体时极化损耗;σs 为标准体的雷达散射截面,m2。
在测试过程中,将雷达方程中难以直接测量且只与雷达系统本身密切相关的各参数由雷达标定常数K 表示为:
| $ {{K}} = \frac{{{{(4\pi )}^3}{{{L}}_P}{{{L}}_t}{{{L}}_r}}}{{{{{G}}^2}{\lambda ^2}}} = \frac{{\sigma {{{P}}_t}}}{{{{{P}}_r}{{{R}}^4}{{L}}_m^2}}{\text{。}} $ | (5) |
由于标准体的 RCS 是已知量,通过对标准体测量,可求得雷达定标常数K。
舰船雷达散射截面与舰船在雷达波照射下后向散射回波功率、雷达发射功率、舰船与雷达的距离有关,将雷达常数K 值代入式(6),得到舰船 RCS 测量值。
| $ \sigma = {{K}}{{{P}}_r}{({{R}})^4}{{{L}}_m}^2/{{{P}}_t}{\text{。}} $ | (6) |
为了保障舰船 RCS 测量精度,提出 RCS 测试需求。
3.1 测试所需信噪比RCS 动态测量过程舰船与背景信号之间的关系如下式:
| $ {\sigma _A} + {\sigma _B}-2\sqrt {{\sigma _A} \cdot {\sigma _B}} \leqslant \sigma \leqslant {\sigma _A} + {\sigma _B} + 2\sqrt {{\sigma _A} \cdot {\sigma _B}} {\text{。}} $ | (7) |
式中:σA 为舰船真实 RCS;σB 为背景真实 RCS;φ 为舰船回波与背景回波之间的相对相位。
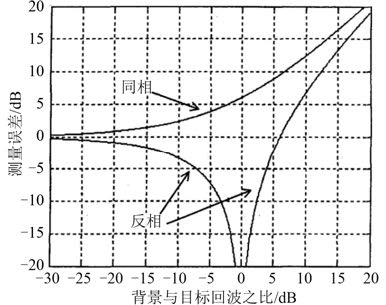
从图 1 可看出,满足测量 ± 1 dB 精度要求,测量累积信噪比一般要大于 20 dB。
|
图 1 雷达散射截面测量误差上下限与信噪比的关系 Fig. 1 The relationship between the radar cross section measurement error and the signal to noise ratio |
在测试舰船雷达散射截面过程中,照射舰船的雷达波幅度和相位必须是均匀的或工程上可接受的平面波,于是可得到经典的 RCS 远场测量条件为:
| $ {{R}} \geqslant 2\frac{{{{{D}}^2}}}{\lambda } $ | (8) |
式中:R 为被测舰船距离,m;D 为测量雷达视轴线垂直方向上的舰船最大尺寸,m;λ 为雷达波长,m;
对于高频动态测量,远场条件一般可修正为常用远场条件的 0.2~0.5 倍。
3.3 近场测试由于测试海域环境和测量设备的限制,有时测试过程很难满足远场测量条件。依据梅林理论,在比经典远场条件小得多的近距离上测得的散射截面随方向角的变化曲线σr (φ)经过一定角度φc 平均后,与在R = ∞ 时测得的σ∞(φ)经φc 平均后的结果相同。测量距离与角度宽度关系为:
| $ {{{R}}_{\min }} = \frac{{720{{D}}}}{{\pi {\varphi _c}}}(1-\frac{{27}}{{\pi {\varphi _c}{{FD}}}}){\text{。}} $ | (9) |
式中:F 为雷达测量频率,GHz;φc 为角度宽度;R 为被测舰船距离,m;D 为测量雷达视轴线垂直方向上的舰船最大尺寸,m。
3.4 测试距离选择测试距离应满足下列条件:
1)最远测试距离
在 RCS 测试过程中,测量系统需对被测舰船进行完全照射,测量距离应不大于天线中心高度处的有效视距,如下式:
| $ {{{R}}_{\text{最远}}}={\rm{4}}{\rm{.12}} \times {\rm{1}}{{\rm{0}}^{\rm{3}}}\sqrt {{H}}{\text{。}} $ | (10) |
式中:R最远 为最远测量距离,m;H 为天线中心距海平面高度,m;b 为最近测试距离。
测试过程中,应满足雷达主波束完全覆盖舰船,如下式:
| $ {{{R}}_{\text{最近}}} > 1.5{{D}}/\theta{\text{。}} $ | (11) |
式中:R最近 为最近测量距离,m;D 为舰船最大尺寸,m;θ 为天线半功率波瓣宽度,rad。
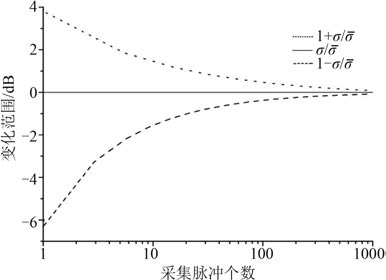
3.5 测量数据样本量要求舰船由许多散射体构成,由于散射体之间相互干涉,舰船的散射信号发生起伏,可以用统计模型来描述其特性。脉冲个数与均值精度的关系如图 3 所示,其中,∆σ 是 RCS 标准偏差, σ 是 RCS 均值。从图 2 可看出,累计 7 个脉冲变化范围在 ± 2 dB,要保障变化范围在 ± 1 dB之内,需累计 25 个脉冲以上,在实际应用中,推荐 RCS 测量数据点 50~256 个脉冲平均。
|
图 2 采集脉个数与均值精度的关系 Fig. 2 Relationship between the number of pulses and the mean accuraly |
用统计方法和数据处理方法完成舰船 RCS 数据处理。
4.1 统计方法 4.1.1 算术平均值和标准偏差的计算1)算术平均值
统计窗口宽度内或扇形区内的动态 RCS 算术平均按下式计算:
| $ \bar \sigma = \frac{1}{{{N}}}\sum\limits_{i = 1}^n {{\sigma _i}} {\text{。}} $ | (12) |
式中:N 为待统计角扇区范围内的 RCS 数据总数。
2)标准偏差
标准偏差STD 按下式计算:
| $ {{STD}} = {\left[ {\frac{{\sum\limits_{i = 1}^N {{{({\sigma _i}-\bar \sigma )}^2}} }}{{{{N}}-1}}} \right]^{\frac{1}{2}}}{\text{。}} $ | (13) |
式中:σi 即可以是线性空间的值,也可以是对数空间的值; $\bar \sigma $为对应空间上的均值;STD 为对应空间上的标准偏差。
4.1.2 概率密度函数和累积分布函数舰船动态 RCS 数据离散的概率密度函数PDF 和累积分布函数CDF 的计算如下:
概率密度函数定义为雷达散射面积位于σ0 和σ0 +dσ 之间的概率P 按下式计算:
| $ {{P}}({\sigma _0} \leqslant \sigma \leqslant {\sigma _0} + {\text{d}}\sigma ) = \int_{{\sigma _0}}^{{\sigma _0} + d\sigma } {PDF(\sigma ){\rm{d}}\sigma } {\text{,}} $ | (14) |
累积分布函数为:
| $ {{CDF}}(\sigma ) = \int_{-\infty }^\sigma {PDF(\sigma ){\rm{d}}\sigma } {\text{。}} $ | (15) |
统计分析中,有时也常用X% 概率的 RCS 值,记作σx% 计算公式为:
| $ {{CDF}}({\sigma _x}) = \int_{-\infty }^{{\sigma _x}} {{{PDF}}(\sigma ){\text{d}}\sigma = x\% } {\text{。}} $ | (16) |
中位值或称中值,是出现概率为 50% 的 RCS 值,一般记作σ50。取累积分布函数CDF = 0.5,可表示为:
| $ CDF({\sigma _{50}}) = \int_{-\infty }^{{\sigma _{50}}} {PDF(\sigma ){\text{d}}\sigma = 0.5} {\text{。}} $ | (17) |
式中:PDF 为概率密度函数;CDF 为累积分布函数。
4.2 处理方法1)扇形区间窗口和阀值的确定
在求平均值或取中值时,必须确定连续取多少个数据点,实际上就等于选择一个统计的角度窗口宽度。
该窗口宽度须根据以下 2 个因素而定:一是舰船姿态相对于雷达视线的变化范围,对于海上舰船,由于风浪的影响,它对雷达视线的变化可达 ± 5°,甚至还大;二是舰船的散射起伏特性,其理论准则是在选定的窗口内至少要包括 3~4 个起伏波瓣。通常这个窗口宽度的典型值在 1°~10°,随不同型号舰船具体情况而定。
2)滑动步长
在确定角度窗口宽度的同时,还必须选择滑动步长,即角度窗口每次沿 RCS 散射图的移动量。滑动步长可以小到等于数据采集时的角度分辨力,即每次只有一个新的数据进入待统计的集合,同时舍去最老的一个数据。滑动步长也可以大到与窗口宽度本身一样大,因此每次取来进行处理的是一整套全新的数据。显然,滑动步长过大,处理结果将过于粗疏;反之,滑动步长越小,生成的散射图越精细,但所需的处理时间也长,简化处理后的数据起伏仍然很大。其大小根据具体要求而定,对舰船数据处理而言 1°、2° 或 5° 都是惯常采用的。
3)二次采样和移动平均
动态舰船 RCS 测量中,一定扇区范围内的 RCS 原始数据往往存在分布不均匀的特性。为了消除这种不均匀性给统计处理带来的影响,可以根据等间隔的方位角原始记录数据进行二次采样,也可以根据雷达方位角和舰船航向角的对应关系,转换成舰船舷向与 RCS 对应关系,移动平均是利用二次采样,对动态 RCS 高速采样的原始数据,用一个平均值来代替该时刻若干个密集采样点的方法。这种方法既压缩了数据量,又起到了增强信杂比的效果。
4)特征值统计
对实测舰船 RCS 数据统计,反映舰船不同舷向雷达散射特性的特征值。
为获取舰船的 RCS 量级,对舰船回旋状态下的 RCS 方向特性测量数据进行全舷向(360°)综合统计,统计出全方位 RCS 最大值、最小值、中值、均值和均方差值。
舰船的 4 个特征方向(舷角为 0°,90°,180°,270°)是测量分析和研究的重点。对上述特定舷向窗口区间内的 RCS 值进行综合统计,得出这些特定区间内的 RCS 最大值、最小值、中值、均值和均方差值。
5 结 语舰船 RCS 测试是一个复杂的过程,通过本文阐述的测试和数据处理方法,获取舰船原始 RCS 测试数据,并进行相应的数据处理,确保了 RCS 测量的可信性和置信度,满足各种电子武器试验对舰船电磁散射特性的需求。
| [1] | 何国瑜, 卢才成, 洪家才, 等. 电磁散射的计算和测量[M]. 北京: 北京航空航天大学出版社, 2006 : 244 -245. |
| [2] | 聂在平, 方大纲. 目标与环境电磁散射特性建模[M]. 北京: 国防工业出版社, 2009 : 367 -370. |
| [3] | 黄培康. 雷达目标特征信号[M]. 北京: 宇航出版社, 1993 : 223 -239. |
| [4] | 黄培康, 殷红成, 许小剑. 雷达目标特性[M]. 北京: 电子工业出版社, 2005 : 112 -114. |
| [5] | SKOLNIK M I. 雷达手册[M]. 南京电子技术研究所, 译. 北京: 电子工业出版社, 2010 : 566 -567. |
| [6] | 庄钊文, 袁乃昌. 雷达散射截面测量[M]. 长沙: 国防科技大学出版社, 2000 : 7 -8. |
| [7] | 航天工业总公司. 目标雷达散射截面数据格式要求:GJB[S]. 1999:3830-1999. |
| [8] | 陈勇, 董纯柱, 王超, 等. 基于HPP/PO的舰船与海面耦合散射快速算法[J]. 系统工程与电子技术 , 2008, 30 (4) :589–592. |
 2016, Vol. 38
2016, Vol. 38
