声呐系统捕捉到目标信号后,需要对目标进行实时测向,给出目标精确的方位值。因此,目标的测向精度是声纳系统的一项重要的技术指标。波束形成方法能够提供阵增益和目标方位估计,是声呐系统用于测向的主要方法。常规的波束形成方法所提供的阵增益有限,抑制噪声的能力不强,方位估计精度不高。Macdonald 和 Schultheiss 的研究表明分裂波束形成方法具有接近最优的目标方位估计精度[1],能够有效提高对目标的分辨能力,这种方法目前在线列阵精确测向中已得到广泛应用[2-7]。
互谱方法和超波束方法是 2 种高分辨率的分裂阵波束形成方法,其共同点是将均匀线列阵等分为左右 2 个子阵,通过时延补偿分别进行左波束形成和右波束形成,不同点在于对左右波束形成的处理。超波束方法由于其对左右波束采取和差运算,对分辨力的改善要明显优于互谱方法,但是由于进行了绝对值运算,使得输出的结果中缺少了相位信息。本文结合互谱和超波束 2 种技术,采用一种新的方法,即超波束互谱测向方法,将超波束形成得到的方位谱加权到互谱结果上,既能够改善主瓣、抑制旁瓣,又能保留相位信息。通过实验室水池测试,验证了该方法的可行性和有效性。
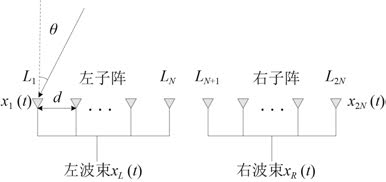
1 超波束互谱测向法均匀线列阵分裂波束形成的原理如图 1 所示[8],总阵元数为 2N 的均匀线列阵,相邻 2 个阵元之间的间隔为d,目标入射角为θ,将阵列等分为左右 2 个子阵,每个子阵各有N 个阵元,其中左子阵L1,L2,…,LN ,右子阵LN+1,…,L2N,左子阵波束输出记为xL (t),右子阵波束输出记为xR (t)。
|
图 1 均匀线列阵分裂波束形成原理图 Fig. 1 Schematic diagram of uniform linear array split beam forming |
以第 1 个阵元为参考阵元,预成波束为阵元法线方向,对于单频信号f0,设第i 个阵元接收的信号为:
| $ {s_i}(t) = \cos (2\pi {f_0}(t + {\tau _i}(\theta ))){\text{,}} $ | (1) |
式中:τi
(θ)为第i 个阵元和第 1 个阵元的输出信号时延差,
则左、右波束信号的时域输出分别为
| $ \begin{aligned} {x_L}(t) = \sum\limits_{i = 1}^N {\cos [2{\rm{\pi }}{f_0}(t + {\tau _i}(\theta ))]} = \displaystyle\frac{{{\rm{sin}}\frac{{N{\rm{\pi }}d\sin \theta }}{\lambda }}}{{{\rm{sin}}\displaystyle\frac{{{\rm{\pi }}d\sin \theta }}{\lambda }}}\; \times \\ {\rm{cos}}(2{\rm{\pi }}{f_0}t + /ok\frac{{(N-1){\rm{\pi }}d\sin \theta }}{\lambda }){\text{,}} \end{aligned} $ | (2) |
| $ \begin{aligned} \!\!\! {x_R}(t) = & \sum\limits_{i = N + 1}^{2N} {\cos [2\pi {f_0}(t + {\tau _i}(\theta ))]} = \frac{{{\text{sin}}\frac{{N\pi d{\text{sin}} \theta }}{\lambda }}}{{{\text{sin}}\frac{{\pi d{\text{sin}} \theta }}{\lambda }}}\ \times \\ & {\text{cos}} (2\pi {f_0}t + \frac{{(3N-1)\pi d\sin \theta }}{\lambda }){\text{。}}\quad\quad \end{aligned} $ | (3) |
由以上可得,左右波束时延差τ 为:
| $ \tau = \frac{{Nd\sin \theta }}{c}{\text{。}} $ | (4) |
对各阵元信号进行傅里叶变换,得到各阵元频域信号Si (f),令参考阵元的频域信号为S(f)。
则左、右波束信号的频域输出分别为:
| $ {X_L}(f) = X(f)\exp \left[ {j\pi f\frac{{\left( {N-1} \right)d\sin \theta }}{c}} \right]{\text{,}} $ | (5) |
| $ {X_R}(f) = X(f)\exp \left[ {j\pi f\frac{{\left( {3N-1} \right)d\sin \theta }}{c}} \right]{\text{。}} $ | (6) |
其中
可以得到左右波束输出的互功率谱:
| $ {\varPhi _{LR}}(f) = {X_L}(f) \cdot {X_R}(f) = {\left| {X(f)} \right|^2}\exp (j2\pi f\tau ){\text{。}} $ | (7) |
对左右波束进行超波束计算,可得到
| $ \begin{aligned} {X_H}(f) = & {\left[ {{{\left( {\left| {{X_L}(f)} \right| + \left| {{X_R}(f)} \right|} \right)}^n}-{{\left| {{X_L}(f)-{X_R}(f)} \right|}^n}} \right]^{\frac{1}{n}}}=\\ & 2\left| {X(f)} \right|{\left[ {1-{{\left| {\sin \frac{{N\pi d\sin \theta }}{\lambda }} \right|}^n}} \right]^{\frac{1}{n}}}{\text{。}} \end{aligned} $ | (8) |
将超波束得到的谱信息加权到互谱得到的结果上,得到最终的波束输出为:
| $ Y(f,{\theta _m}) = \frac{{{X_H}(f,{\theta _m})}}{{\sum\limits_m {{X_H}(f,{\theta _m})} }}{\varPhi _{LR}}(f,{\theta _m}){\text{。}} $ | (9) |
其中m 为波束号。
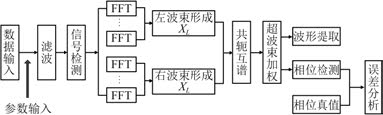
2 试验研究 2.1 实验室测试在实验室消声水池中,利用接收阵对中心频率为 37.5 kHz 的声源信号进行测向试验。接收阵为 1 条 16 元均匀直线阵,阵元间距为 0.016 m,采集器滤波设置为 20~50 kHz,信号采样率为 500 kHz。声源与接收阵的距离为 6 m,消声水池中基阵与声源吊放深度为水下 3 m,水温 14 °。针对不同的测试角度采集基阵相应的数据,每组测试时间 20 s。分裂阵频域波束测向分辨力的检测数据处理流程如图 2 所示,其中超波束指数n 为 0.5。
|
图 2 分裂阵频域波束形成处理流程 Fig. 2 Process flow of split array beam forming in frequency domain |
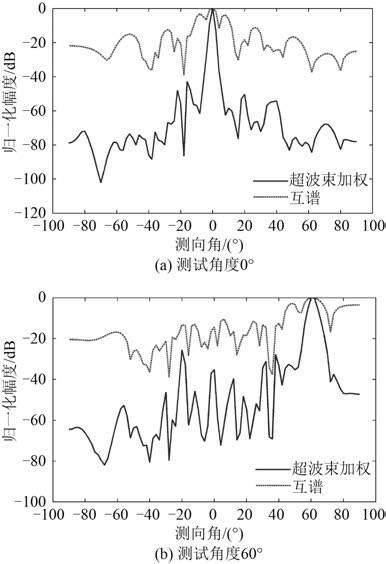
根据实验室实测数据得到超波束互谱方法和互谱方法指向性曲线对比如图 3 所示,图中的测试角度分别为 0° 和 60°。与互谱方法相比较,超波束互谱方法在 0° 和 60° 的主瓣宽度分别减小了 3.8° 和 6.9°,旁瓣幅度降低超过 30 dB,测向分辨力得到提高,从而验证了超波束互谱测向方法的可行性和有效性。
|
图 3 超波束互谱方法与互谱方法指向性曲线对比 Fig. 3 Comparison of detective patterns for the hyper beam & cross spectrum method and the cross spectrum method |
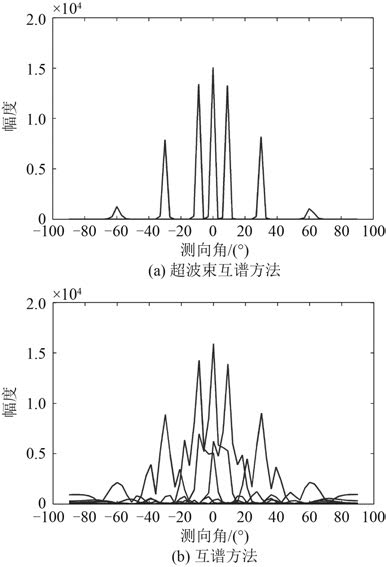
图 4 为各测试角度的能量对比图,测试角度为 0°,± 9°,± 30° 和 ± 60°,可以看到超波束互谱方法与互谱方法相比,减小了主瓣宽度,降低了旁瓣幅度,虚警概率减小,分辨力明显提高,并且保证了各测试角度能量的分布趋势一致。
|
图 4 能量对比 Fig. 4 Power comparison |
超波束指数、阵元个数及个别阵元失效等情况会影响到测向分辨力,下面给出超波束互谱方法和互谱方法 2 种情况下各因素对分辨力的影响分析。
1)超波束指数的影响
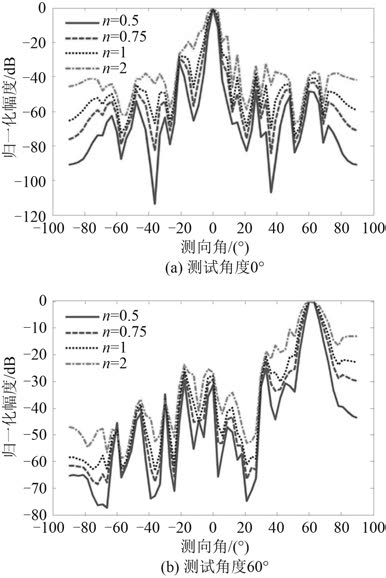
图 5 是超波束指数对分辨力的影响分析图。图中的测试角度分别为 0° 和 60°,可以看到随着超波束指数n 的增大,主瓣宽度变宽,旁瓣幅度变大,测向分辨力变差,因此基于分辨力的考虑,n 值越小越好,通常n 的取值范围为(0~1)。但n 值太小可能会出现较大的解算值误差,并且性能稳定度也会降低,在实际情况中应折中考虑,在不出现较大的解算值误差的范围内,选取能够最大限度提高分辨力的n 值。
|
图 5 超波束指数n 对分辨力的影响 Fig. 5 Effect of hyper beam indexn on resolution |
2)阵元数的影响
阵元数是影响测向分辨率的主要因素,图 6 是阵元数对分辨力的影响分析图,图中测试角度为 60°。可以看出,相同阵元间距情况下,阵元数越多,阵列的有效孔径越大,测向分辨力越高。并且进行超波束加权之后,对相同阵元数线列阵来说,分辨力有明显提高。

|
图 6 阵元数对分辨力的影响 Fig. 6 Effect of array number on resolution |
3)阵元损坏的影响
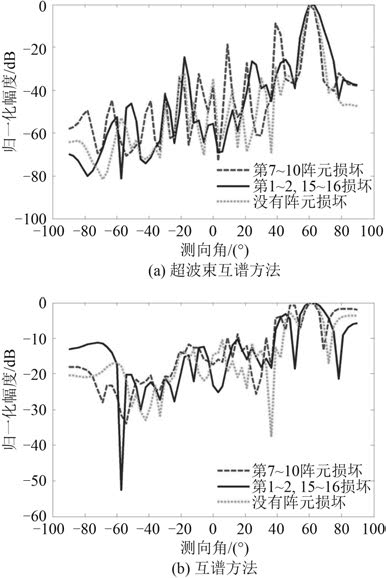
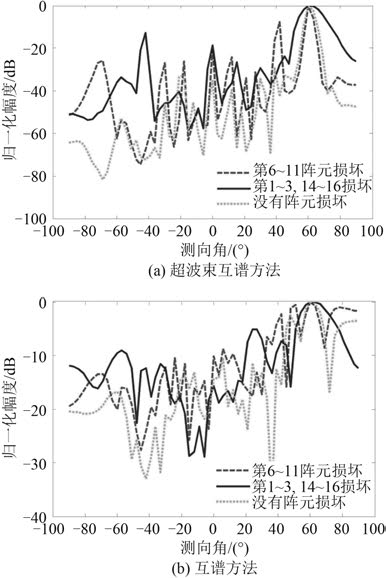
某 1 个或几个阵元损坏会对分裂阵频域波束形成的测向分辨力产生影响。图 7 和图 8 中分别为 16 元均匀线列阵中有 4 个阵元损坏和有 6 个阵元损坏的情况,测试角度为 60°。横向对比,无论是分裂阵中心阵元损坏还是两端阵元损坏,超波束互谱方法分辨力的恶化的程度要明显小于互谱方法的情况。分裂阵中心连续阵元损坏后,主要影响曲线的旁瓣,使旁瓣变大,增加了虚警的概率,而两端阵元损坏后主要影响曲线的主瓣,使主瓣变宽,降低检测能力。这种现象同样可以在有 6 个阵元损坏的情况下看到。纵向对比,阵元损坏的个数越多,分辨力越差。但如果阵元数损坏过多,会造成测向结果的失效,因此在实验过程中应及时检查各阵元的健康状况,保证没有或尽量少的阵元损坏,避免因阵元损坏而影响测向结果。同时也可以看出,超波束互谱测向方法对阵元损坏有更好的容错性。
|
图 7 有 4 个阵元损坏的情况对比 Fig. 7 Cases for 4 array elements damaged |
|
图 8 有 6 个阵元损坏的情况对比 Fig. 8 Cases for 6 array elements damaged |
利用超波束互谱方法进行数据处理的过程中,存在测试角度真值和解算值之间的误差,即解算值误差,上述分析的超波束指数,阵元数以及个别阵元损坏会影响解算值误差的大小。根据实验测试的 25 个角度(0°、± 0.5°,± 1°,± 8°,± 9°,± 12°,± 27°,± 30°,± 33°,± 51°,± 54°,± 57°,± 60°)的数据处理结果,得到各影响因素下的解算值误差如表 1 所示。
|
|
表 1 超波束互谱方法解算值误差影响 Tab.1 Computation error effect of the hyper beam and cross spectrum method |
从表 1 可看出,超波束指数n 取值过小时,会增大解算值误差;阵元数越少,解算值误差越大;16 元分裂阵中阵元损坏个数在 6 个以下时,与无损坏时相比较,对解算值误差的影响不大。对于 16 元线性分裂阵来说,超波束指数n 为 0.75 时,超波束指数和个别阵元损坏影响下的解算值误差最大值不超过 3°,误差均值不超过 0.44°,方差不超过 0.71。可见超波束互谱测向方法具有较高的测向精度。
3 结 语文中提出了一种线性分裂阵频域波束形成的方法,即超波束互谱测向方法,通过实验室测量验证了该方法能够很好地改善主瓣、降低旁瓣,提高测向分辨力,而且能够将互谱输出中的相位信息保留下来,为后续的分析处理提供有效信息。同时分析并总结了超波束指数、阵元数以及个别阵元损坏对分辨力和解算值误差的影响,从侧面验证了该方法具有较高的测向精度,具有实际应用价值。
| [1] | STERGIOPOULOS S, ASHLEY A T. An experimental evaluation of split-beam processing as a broadband bearing estimator for line array sonar system[J]. The Journal of the Acoustical Society of America , 1997, 102 (6) :3556–3563. DOI:10.1121/1.420146 |
| [2] |
钱韬. 线阵分裂波束处理技术在水声探测中的应用[J]. 声学技术 , 2015, 34 (6) :551–555.
QIAN Tao. Application of split-beam processing of line array in underwater acoustic detection[J]. Technical Acoustics , 2015, 34 (6) :551–555. |
| [3] |
李晋, 王晓庆, 陈卫东. 基于常规波束合成的分裂阵互谱定向研究[J]. 无线电工程 , 2016, 46 (2) :36–40.
LI Jin, WANG Xiao-qing, CHEN Wei-dong. Research on cross-spectrum direction-finding with splitting beam based on conventional beam-forming[J]. Radio Engineering , 2016, 46 (2) :36–40. |
| [4] |
郭冉. 水下目标测向算法研究与实时实现[D]. 哈尔滨:哈尔滨工程大学, 2013.
GUO Ran. Research on direction finding algorithm and the real-time implementation of underwater target[D]. Harbin:Harbin Engineering University, 2013. |
| [5] | SCHLIETER H. Passive sonar detection improvement by Hyper-beam technique[C]//Proceedings UDT Europe. 2006. |
| [6] |
周胜增, 刘东涛, 杜选民. 超波束处理在被动声纳频谱分析中的应用[J]. 声学技术 , 2011, 30 (5) :460–462.
ZHOU Sheng-zeng, LIU Dong-tao, DU Xuan-min. Application of hyper-beamforming in spectrum analysis of passive sonar[J]. Technical Acoustics , 2011, 30 (5) :460–462. |
| [7] |
王永丰, 王昭辉. 超波束处理方法的快速实现及试验验证[J]. 声学技术 , 2012, 31 (5) :522–525.
WANG Yong-feng, WANG Zhao-hui. Fast implementation of hyper beam method and its performance evaluation[J]. Technical Acoustics , 2012, 31 (5) :522–525. |
| [8] | 李启虎. 数字式声纳设计原理[M]. 合肥: 安徽教育出版社, 2002 . |
 2016, Vol. 38
2016, Vol. 38
