目前,线阵广泛应用于水下目标波达方向(DOA)估计,并且在实际应用中由于均匀线阵(ULA)结构简单、易于实现,多被采用。均匀线阵在物理阵元数确定的情况下,其分辨率就确定了,要实现高分辨方位估计,一种方法是从算法角度考虑,即软件方面考虑,如多重信号分类(MUSIC)算法[1],在一定条件下,该算法可以有效打破“瑞利限”的限制,实现对多个信号的高分辨 DOA 估计;另一种方法,是从硬件方面考虑,即增加阵元数,以达到孔径的扩展。
实际应用中增加阵元数目将会增加设备层,同时对整个系统的可靠性也带来影响,故很多学者研究通过虚拟出阵元的方法以达到扩展孔径的目的。如通过阵列的匀速运动,将时间增益转换为空间增益的被动合成孔径方法[2];通过高阶累积量扩展孔径的方法[3];通过非均匀布阵,基于冗余度的概念设计的最小冗余线阵,用较少的阵元达到较大的孔径[4]。本文应用文献[5]提出的互素阵的概念来实现阵列孔径的扩展,仿真验证了孔径扩展所达到的高分辨性能,同时消声水池试验验证了其孔径扩展所达到的效果。
1 互素阵孔径扩展 1.1 互素定理令M 和N 是互素数,且M <N,任给一整数k,0≤k≤MN,都存在整数m 和n,使得k =Nm-Mn,其中 0≤m≤2M-1,0≤n≤N-1。选择同样的m 和n 同样也可以产生-k,表示负的差。
互素定理表明在满足一定条件下只需要N + 2M-1 个整数就可以通过 2 个数的差产生 2MN + 1 个连续的整数,这就可以用于非均匀阵列相位相减产生虚拟阵列,下面将详细介绍孔径扩展的方法。
1.2 孔径扩展现假设有N + 2M-1 个阵元够成的非均匀线阵,非均匀线阵在假想的均匀线阵中的序号(位置)如图 1 所示。
| $S=\{Mnd,0nN-1\}\cup \{Nmd,1m2M-1\}$ | (1) |
图中d 为均匀线阵的阵元间距,为半波长,该非均匀阵可看做 2 个均匀的子阵,第 1 个子阵阵元间的间距为Md,且有N 个阵元;第 2 个子阵阵元间的间距为Nd,有 2M-1 个阵元。

|
图 1 互素孔径扩展 Fig. 1 Extended aperture use coprime theorems |
例如当M = 2、N = 3 时,该非均匀阵第 1 个子阵阵元在假想的均匀线阵中的位置为 0,2,4,第 2 个子阵阵元在假想的均匀线阵中的位置为 3,6,9。
根据互素定理,可以由N + 2M-1 个整数,产生出 0≤k≤MN 的任一整数,并且对于均匀线阵接收同一个远场信号s,每个阵元所接收到该信号s 的相位相差为线性,这一点通过均匀线阵的阵列流行向量就可以知道,即 2 个阵元上接收到的信号相位差与这 2 个阵元之间的相对位置D 有关,故只要非均匀线阵的 2 个子阵中阵元位置按互素定理之定义位置来取,则可以通过这 2 个子阵中某 2 个阵元的相位差得到该非均匀线阵中不存在的物理阵元的相位,实际操作中可以使用这 2 个阵元的其中一个阵元接收到的信号与另外一个阵元接收到的信号共轭相乘来实现相位求差。例如M = 2、N = 3 时,k =N·1-M·1 = 1,则由第 1 个子阵的 1 号阵元和第 2 个子阵的 1 号阵元可以产生假想均匀线阵的 1 号阵元(阵元位置从 0 开始排)。
2 仿真实验假设 4 个远场相关信号,声源频率f = 1 000 Hz,入射角度分别为-50°、-20°、10°与 40°,采样频率fs = 15 kHz,水下声速估计为c = 1 500 m/s,假想均匀线阵的间距d = 0.75 m。两非均匀线阵的M = 2,N = 3,按照互素阵孔径扩展方法使用N + 2M-1 个物理阵元,可以得到拥有MN + 1 个阵元的均匀线阵,图 2 为采用互素阵的孔径扩展后对上述 4 个远场声源 DOA 估计的效果与拥有N + 2M-1 个阵元的均匀线阵 DOA 估计的对比,DOA 估计采用的是 MUSIC 方法。

|
图 2 四个目标 DOA 估计对比 Fig. 2 Four target DOA estimation comparison |
由图 2 可知,采用相同的物理阵元数,使用互素孔径扩展后的虚拟阵列 DOA 估计与未扩展的均匀线阵相比,前者具有更高的空间分辨率与更低的旁瓣级,且优势明显。
3 水池实验验证本次试验是在国内某高校消声水池进行的,水池长 20 m,宽 8 m,深 7 m。接收阵为拥有 10 个阵元的垂直均匀线阵,首阵元距水面 0.7 m。
发射信号频率为 3 kHz 的 CW 脉冲,脉冲长度为 400 ms,周期为 1 s。发射换能器距离接收阵为 7 m。
取该垂直均匀线阵的第 0,2,4 阵元作为第 1 个子阵,取第 3,6,9 阵元为第 2 个子阵,进行互素孔径扩展。图 3 为使用常规波束形成(CBF)算法 DOA 估计的结果,将孔径扩展后的 DOA 估计与连续取 0,1,2,3,4,5 阵元的 DOA 估计进行对比;同样的阵元取法,图 4 是使用 MUSIC 算法的进行 DOA 估计的对比。

|
图 3 CBF 算法 DOA 估计对比 Fig. 3 CBF algorithm DOA estimation comparison |
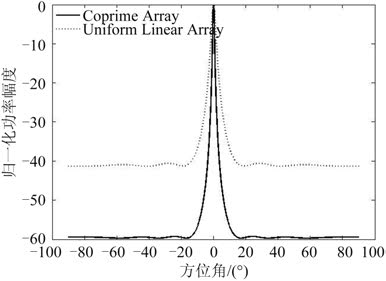
|
图 4 MUSIC 算法 DOA 估计对比 Fig. 4 MUSIC algorithm DOA estimation comparison |
从图 3、图 4 可以看出使用相同的物理阵元数,水池试验验证了互素阵孔径扩展后的 DOA 估计与均匀线阵比较,孔径扩展可以显著地提高空间分辨率并得到更低的旁瓣级。
4 结 语本文通过采用互素阵的孔径扩展方法,对阵列孔径进行扩展,即在相同的物理阵元下,互素阵孔径扩展方法使用 2 个均匀线阵,在间距满足一定的条件下,根据互素定理产生虚拟阵元;从本质上说这是一种非均匀布阵方法,只不过是在阵元间距上做了满足互素定理地要求。仿真和水池试验验证该孔径扩展方法可以显著地提高空间分辨率且能得到更低的旁瓣级,该孔径扩展方法通过非均匀布阵,用N + 2M-1 个物理阵元可以扩展得到MN + 1 的孔径,故可以显著地节省物理阵元,对实际工程来说能降低成本,具有良好的工程应用前景。
| [1] | SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation , 1986, 34 (3) :276–280. DOI:10.1109/TAP.1986.1143830 |
| [2] | STERGIOPOULOS S, SULLIVAN E J. Extended towed array processing by an overlap correlator[J]. The Journal of the Acoustical Society of America , 1989, 86 (1) :158–171. DOI:10.1121/1.398335 |
| [3] |
陈建, 王树勋. 基于高阶累积量虚拟阵列扩展的DOA估计[J]. 电子与信息学报 , 2007, 29 (5) :1041–1044.
CHEN Jian, WANG Shu-xun. DOA estimation of virtual array extension based on fourth-order cumulant[J]. Journal of Electronics&Information Technology , 2007, 29 (5) :1041–1044. |
| [4] |
张利强, 全厚德. 最小冗余线阵的DOA估计[J]. 火力与指挥控制 , 2012, 37 (10) :10–13.
ZHANG Li-qiang, QUAN Hou-de. A study on DOA estimation of minimum-redundancy linear arrays[J]. Fire Control&Command Control , 2012, 37 (10) :10–13. |
| [5] | VAIDYANATHAN P P, PAL P. Sparse sensing with co-prime samplers and arrays[J]. IEEE Transactions on Signal Processing , 2011, 59 (2) :573–586. DOI:10.1109/TSP.2010.2089682 |
 2016, Vol. 38
2016, Vol. 38
