与表面声道相比,深海声道(SOFAR)受季节变化的影响较小,声道效应更加趋于稳定[1]。深海中当满足一定条件时会形成会聚区,Hale[2]较早地在海上实验中观察到会聚区, 并对会聚区进行了一系列研究。Urick[3]分析了不同声源深度时会聚带的变化情况。A.O.Williams[4]指出会聚现象是大量同相简正波叠加的结果。范培勤等[5]分析了深海会聚区现象的形成机理,给出了会聚区距离计算模型。郭李等[6]将会聚区效应应用于定位,给出了一种基于会聚区声强匹配的声源定位方法, 张仁[7]和利用简正波理论讨论了反转点会聚区,前人对会聚区进行了一定的研究,但针对会聚区目标相对强度的特征研究还较少。
本文分析深海会聚区的形成条件,为充分利用会聚区效应实行远程探测提供了基础,同时研究一定深度目标的相对强度在会聚区中的分布特性,为通过会聚区实现目标深度判定提供了一种方法。
1 深海会聚区形成条件 1.1 SOFAR 声道的上限与下限深海声道的上下限定义为声速剖面中在声道轴上下两侧的 2 个相等最大声速所对应的深度,在图 1 中,上下限分别对应于A 和B 点,C 点对应的深度称为声道轴深度。
|
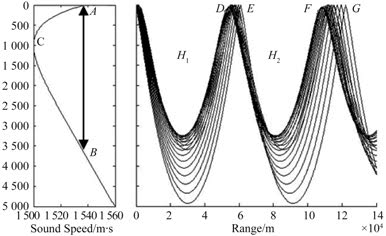
图 1 声源位于 75 m 时对会聚区有贡献的声线 Fig. 1 Rays contribute to the convergence zone when the sound source is located at 75 m |
要形成深海会聚区,首先要存在声速极小值,即C 点,只有这样从声源处发射的声线才能够经过折射在近海底处发生反转在远距离处聚焦。其次发射声线需要满足一定条件,将图 1 中声速分布分为n 层,每层深度为d,上界面声速为
| ${c_r} = c_1^ + /\cos \theta _1^ + = c_1^-/\cos \theta _1^-= \cdots \cdots c_n^-/\cos \theta _n^-{\text {。}}$ | (1) |
式中:
若
图 1 为利用 BELLHOP 模型[8] 仿真得到的对会聚区有贡献的声线分布,仿真采用 Munk 声速剖面[9],声源深度 75 m,仿真水深为 5 000 m,从图中可以看出,声道中有的区域声线不经过海面或海底反射,这样的结果是声道中有的部分出现声线密集区,如DE 区(第一会聚区)、FG 区(第二会聚区),有的部分只有有限的从海面和海底反射来的能量,如H1 和H2 区(声影区),从图 1 中可以明显看出,随着距离的增加,会聚区宽度也随之增加(第二会聚区宽度大于第一会聚区宽度)。
2 会聚区目标相对强度计算方法根据 Kraken 模型[8],频率为
| $\!p(r,z,{z_s}) \!=\!\! \frac{i}{{\rho ({z_s})\sqrt {8\pi r} }}{e^{-i\pi /4}}\sum\limits_{m = 1}^\infty {{Z_m}({z_s})} {Z_m}(z)\frac{{{e^{i{k_m}(\omega )r}}}}{{\sqrt {{k_m}(\omega )} }}{\text {。}}\!\!\!$ | (2) |
式中:
声压场
| $s\left( {r,{z_s},z,t} \right) = \frac{1}{{2\pi }}\int_{-\infty }^{ + \infty } {S\left( \omega \right)} p\left( {r,{z_s},z,\omega } \right){e^{-i\omega t}}{\rm d}\omega, $ | (3) |
若目标信号为单频时,
| $s\left( {r,{z_s},z,t} \right) = \frac{{\left| {S\left( \omega \right)} \right|}}{{2\pi }}p\left( {r,{z_s},z,\omega } \right){e^{-i\omega t}},$ | (4) |
其中
| $\bar I = \frac{1}{n}\sum\limits_{i = 1}^n {s\left( {r,{z_s},z,t} \right)} {s^*}\left( {r,{z_s},z,t} \right),$ | (5) |
式中:
| ${I_r}\left( {r,{z_s},z,t} \right) = 10\lg \left( {\frac{{\bar I}}{{{I_0}}}} \right){\text {。}}$ | (6) |
其中
仿真海区水深 5 000 m,水平范围取第一会聚区大致所处距离范围约为 5.1~6.3 km,采用图 1 中所示 Munk 声速剖面,声源频率取 1 000 Hz,仿真声源深度分别取 35 m,50 m,60 m,70 m,75 m,105 m,接收深度取 60 m,85 m,110 m,160 m。
|
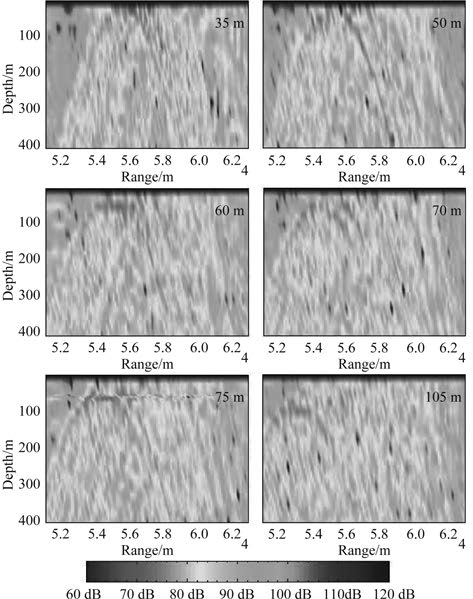
图 2 第一会聚区不同深度声源对应的传播损失 Fig. 2 TL corresponding to different sound source depths in the first convergence zone |
图 2 所示为第一会聚区不同深度声源对应的传播损失图,纵轴为水深,截取深度范围 0~400 m,横轴为距离,取第一会聚区范围,图中由上至下,由左至右依次对应声源深度 35 m,50 m,60 m,70 m,75 m,105 m 处的传播损失,从图中对比我们可以看出,随着声源深度的增加,会聚区宽度总体上也随之增加,整体声强逐渐减弱。
|
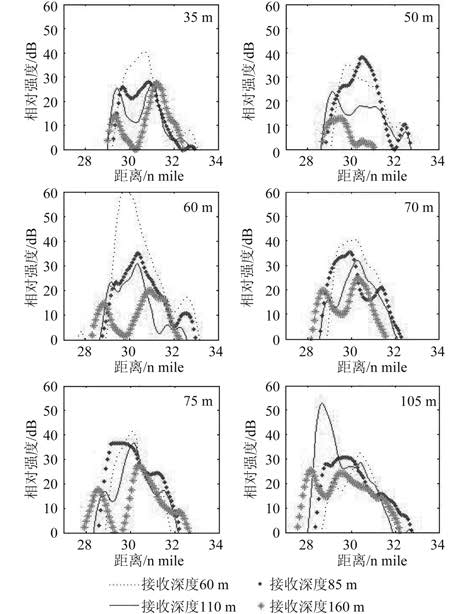
图 3 第一会聚区不同接收深度处的目标相对强度 Fig. 3 The relative sound intensity corresponding to different receiving depths in the first convergence zone |
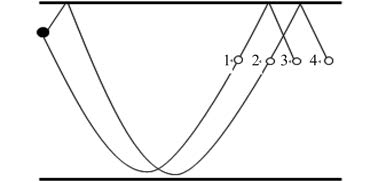
图 3 为第一会聚区声源深度为 35 m,50 m,60 m,70 m,75 m,105 m,对应接收 60 m,85 m,110 m,160 m 的目标相对声强的分布图。从图中可看出,相对强度随距离的分布总体存在 2 个峰值,这是由于声源形成会聚区将使会聚区中强度分布形成 4 个峰:第 1 个峰是由声源发出,向下在足够深处反转,到达接收点而形成的。第 2 个峰由声源发出,先经过海面反射,而后在水层深处反转,到达接收点而形成的。第 3,4 峰是由形成第 1,2 峰的声线,经过海面反射,而后到达接收点而形成的。形成 4 个峰的典型声线如图 4 所示,分别标以 1,2,3,4。由图 4 可看出,当声源深度确定时,第 1,3 峰和第 2,4 峰之间的间隔则决定于接收器的深度,当接收深度并不深时,第 1,2 峰及第 3,4 峰之间间隔很短,当第 1,3 峰刚刚下降的时候,第 2,4 峰已经开始出现,1,2 峰与 3,4 峰分别互相叠加,最终形成了 2 个峰值。
|
图 4 第一会聚区相对强度峰值形成示意图 Fig. 4 Forming principle of the peak of the relative sound intensity in the first convergence zone |
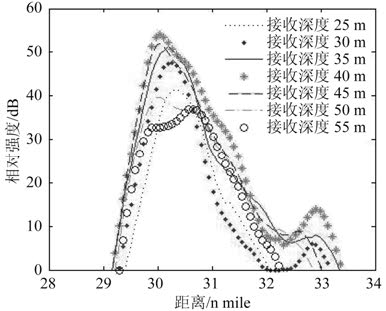
同时,从图 3 中可看出,当接收深度接近声源深度时,目标的相对强度相较于其他接收深度要高得多,为了进一步分析确定深度的目标相对声强与接收深度的关系,取一个个例,将接收深度的间隔取小,如图 5 所示,声源深度为 40 m,会聚区内接收深度依次为 25~55 m,间隔 5 m,从图 5 可看出,接收深度向声源深度靠拢时,相对强度增大,在声源深度处相对强度达到最大值,这样可通过分析声呐在不同深度接收到的声信号的相对声强,获取目标声源的深度信息。
|
图 5 声源深度为 40 m 时第一会聚区相对强度 Fig. 5 The relative sound intensity of the first convergence zone when the source depth is 40 m |
本文分析了深海会聚区的特性以及一定深度目标的相对强度在会聚区中的分布特征,得出了以下结论:
1)当存在声速极小值以及反转声线,且出射声线满足
2)会聚区目标相对强度分布具有双峰结构。
3)当接收深度与目标深度相同时,目标相对强度会出现峰值,这为通过会聚区实现目标深度判定提供了 1 种方法,具有重要的应用价值。
| [1] | 刘伯胜, 雷家煜. 水声学原理[M]. 哈尔滨: 哈尔滨工程大学出版社, 2006 . |
| [2] | HALE f E. Long-range sound propagation in the deep ocean[J]. The Journal of the Acoustical Society of America , 1961, 33 (4) :456–464. DOI:10.1121/1.1908691 |
| [3] | URICK R J. Principles of underwater sound[M]. New York: McGraw-Hill, 1983 . |
| [4] | WILLIAMS JR A O, HORNE W. Axial focusing of sound in the SOFAR channel[J]. The Journal of the Acoustical Society of America , 1967, 41 (1) :189–198. DOI:10.1121/1.1910316 |
| [5] | 范培勤, 笪良龙, 李玉阳. 深海会聚区特征参数计算方法研究[J]. 海洋技术 , 2012, 31 (4) :23–25. |
| [6] | 郭李, 宋志杰, 王良. 基于深海会聚区声强匹配处理的声源定位方法[J]. 声学技术 , 2012, 31 (3) :277–281. |
| [7] | 张仁和. 水下声道中的反转点会聚区(Ⅰ)简正波理论[J]. 声学学报 , 1980 (1) :28–42. |
| [8] | 汪德昭, 尚尔昌. 水声学[M]. 2版. 北京: 科学出版社, 2013 . |
| [9] | 艾特. 水声建模与仿真[M]. 蔡志明, 译. 3版. 北京: 电子工业出版社, 2005 . |
 2016, Vol. 38
2016, Vol. 38
