2. 吉宝(南通)重工有限公司工程部, 江苏 南通 226010
2. Keppel(Nantong) Industry Limited Company, Engineering Department, Nantong 226010, China
随着计算机技术的发展,各类先进的仿真软件如 Fluent,CFX 在船舶与海洋结构物概念设计优化过程中得到了广泛的应用和发展。然而,在优化设计过程中,很难将这些软件直接与优化器结合,因为优化设计过程中需要很多次迭代才能获得最优方案,而每进行一次仿真需要消耗大量的计算时间。近似建模技术成为解决上述问题的有效途径。李冬琴等[1]以海洋平台支持船操纵性为研究对象,采用多种试验分析方法进行取样,根据样本点及操纵响应值完成了近似模型的构建;肖振业等[2]以国际标模 KCS 为例,利用支持向量机理论建立船舶的总阻力近似模型,并与神经网络建立的近似模型进行对比,验证了支持向量理论建立近似模型的可行性;孙丽娜等[3]在三体船侧体布局及型线优化设计研究中建立总阻力的神经网络预测模型;常海超等[4]以国际标模 KCS 为例,建立了船舶阻力性能的神经网络近似模型,研究了样本点对近似模型精度的影响;程妍雪等[5]结合有限元方法和近似模型技术对其耐压特性进行分析,得到复合材料增强纤维的含量与耐压壳结构性能参数的关系。
在潜器概念设计优化过程中,潜器流体动力学性能参数的获取往往采用有限元方法,这样导致潜器外形优化仍然是一个漫长的过程。因此,本文研究了基于支持向量回归(Support Vector Regression,SVR)模型的潜器外形优化方法,包括拉丁超立方试验设计选取样本点、基于 ICEM 的潜器参数化建模和网格自动划分、基于 Fluent 的阻力计算及 SVR 模型的构造。采用改进的粒子群优化,获得了阻力性能优良的潜器外形。
1 SVR 近似模型支持向量回归(Support Vector Regression,SVR)模型是支持向量机(Support Vector Machine,SVM)在线性/非线性回归问题中的应用,最初由 Vapnick 在 20 世纪 90 年代提出。SVR 自提出以来,受到广泛关注,在多个领域取得良好的应用,成为解决“非线性和维度灾难问题”、“过拟合问题”和“多个局部极小值问题”等难题的强有力手段[6-8] 。
给定 1 组训练样本 $D = \{ ({x_1},{y_1}),({x_2},{y_2})...$$({x_i},{y_i})...({x_n},{y_n})\} {x_i} \in {R^N},{y_i} \in R,{\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2...n$,其中xi 为设计变量,yi 为xi 处对应的响应。ε-SVR 是常用的一种 SVR,它利用非线性映射φ(x)将样本转换到高维空间 $\varphi (x) = (\varphi ({x_1}),\varphi ({x_2}),...,\varphi ({x_n}))$,并找到一个线性函数f(x)最小化训练样本处的预测误差,使f(x)最多离训练样本处的响应有ε 的偏差,这样,原空间中的非线性拟合问题就变为高维空间的线性问题。该函数N 可以表示如下:
| $ f(x) = {{w}^{\rm T}}\varphi ({x}) + b $ | (1) |
式中:φ( x )为 1 组非线性转换; w 为权重向量, w 范值越小,SVR 模型的复杂度越小;b 为偏差量。
在式(1)中引入松弛变量ξi 和ξi *,ε-SVR 的优化问题可以转化为下式:
| $ \begin{array}{l} {\rm{min}}\;\;\frac{1}{2}{{w}^{\rm T}}{w} + C\sum\limits_{i = 1}^n {({\xi _i} + \xi _i^*)}, \\ {\rm s}.{\rm t}.\;\;\left\{ {\begin{array}{*{20}{c}} {{y_i}-{{w}^{\text{,}}}\varphi ({{x}_i})-b \leqslant \varepsilon + {\xi _i}},\\ {{{w}^{\text{T}}}\varphi ({{x}_i}) + b-{y_i} \leqslant \varepsilon + \xi _i^*},\\ {{\xi _i},\xi _i^* \geqslant 0}{\text {。}} \end{array}} \right. \end{array} $ | (2) |
其中C 为平衡模型复杂度和训练误差的正规化参数(也称为惩罚参数),合适的C 值能使模型具有较好的推广能力。
LSSVR 引入了线性最小二乘规则,上式中的不等式约束转化为了等式约束。LSSVR 可以用以下公式描述:
式中的前半部分的 $\frac{1}{2}{{w}^{\rm T}}{w}$ 用来归一化大的权重值和惩罚值。后半部分表示回归误差,由
| $ \begin{array}{l} {\rm{min }}\frac{1}{2}{{w}^{\text{T}}}{w} + \frac{1}{2}C\sum\limits_{i = 1}^n {e_i^2}, \\ {\rm s}.{\rm t}.{\rm{ }}{e_i} = {{\rm{y}}_i}-{{w}^{\text{T}}}\varphi ({{x}_i})-b,i = 1,2...n{\text {。}} \end{array} $ | (3) |
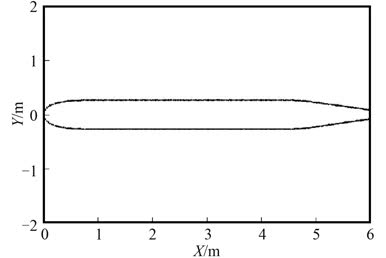
本文所采用的潜器属于流线形回转体型线表达式设计的线型(见图 1)。潜器线型几何参数:总长L = 6 m,头部曲线段长LM = 1 m,圆柱段长LH = 3.5 m,尾部总长LT = 1.5 m,最大直径D0 = 0.533 4 m,头尾部曲线段都采用双参数椭圆线型。
|
图 1 流线形回转体 Fig. 1 Streamline body of rotation |
潜器头部曲线段所采用的物理线型方程为:
| $ y = \frac{{{D_0}}}{2}{\left[ {1-{{\left( {1-\frac{X}{{{L_H}}}} \right)}^{{x_2}}}} \right]^{1/{x_1}}}, $ | (4) |
潜器尾部曲线段所采用的物理线型方程为:
| $ y = \frac{{{D_0}}}{2}{\left[ {1-{{\left( {X-{L_H}-{L_M}} \right)}^{{x_4}}}} \right]^{{x_3}}}{\text {。}} $ | (5) |
式中:x1 和x2 为头部椭圆线型的双参数;x3 和x4 为尾部椭圆线型的双参数。其取值范围:0 ≤x1 ≤ 1,0 ≤x2 ≤ 20,3 ≤x3 ≤ 11,0 ≤x4 ≤ 0.2。
2.2 基于 SVR 近似模型的潜器阻力模型构建常用的试验设计方法包括正交试验设计(Orthogonal Experiment Design),均匀试验设计(Uniform Experimental Design Method)、拉丁超立方试验设计方法(Latin Hypercube Designs)等。鉴于本文中存在 4 个设计变量,且每进行 1 次计算机仿真耗时 8 h,本文选取能以最少试验样本点达到设计空间均匀填充的优化拉丁超立方实验设计方法作为样本点的选取方法。该方法中,假设总设计样本点数目为N,那么每个设计变量将会被等分为N 份,每一个等分里面将填充一个样本点[9]。采用优化拉丁方生成 16 个样本点,如表 1 所示。
|
|
表 1 阻力系数计算结果 Tab.1 Calculations of drag coefficients |
为避免每次改变潜器外形,都需要重新建模,本文使用 Fortran 语言自编程自动生成不同参数下的线型型值。通过 jou 日志文件记录第 1 次 ICEM 网格划分流程,采样 Flunet 调用 ICEM 进行 16 组样本点的阻力系数计算。本文采用的仿真模型为三维模型,其中潜器附近进行网格加密(见图 2),以保证建立 SVR 模型的试验设计的顺利进行。Fluent 计算过程中采用有限体积法,即在控制体内进行积分,然后离散得到线性方程,以保证控制体内的物理量守恒。对流项使用二阶迎风差分,对于扩散项和源项也均采用二阶迎风差分,采用 SIMPLEC 法修正压力。各参数的残差值均为 10-4。

|
图 2 潜器网格模型 Fig. 2 Submersible grid model |
16组参数下的阻力系数计算结果的汇总见表 1。
为了评价 SVR 模型的拟合精度,选择均方误差(RMSE)和相关系数R2 作为精度评价准则[10],随机选择 6 个验证样本,比较了多元响应面(PRS)、BP 神经网络(BPNN)、径向基函数(RBF)及 Kriging 模型的拟合效果。结果列入表 2 中。由表 2 可得出,对于该近似建模问题,SVR 近似模型得到的均方误差最小,相关系数最大,拟合性能最佳。
|
|
表 2 近似性能比较结果 Tab.2 Approximate performance comparison results |
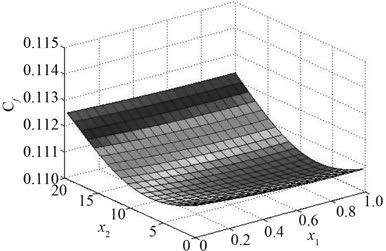
图 3 为仿真结果与 SVR 预测结果的关系。由精度评价准则值和图 3 可知,SVR 模型的近似程度很高。能用来替代仿真模型进行优化设计。图 4~图 7 分别为潜器阻力系数各个不同参数组合下构建的 SVR 近似模型。

|
图 3 仿真结果与预测结果的关系 Fig. 3 Relationship between simulation and prediction results |
|
图 4 x1,x2 与潜器阻力系数的近似关系 Fig. 4 Approximate relationship betweenx1,x2 and drag coefficients |
|
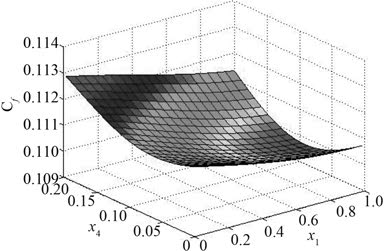
图 5 x1,x4 与潜器阻力系数的近似关系 Fig. 5 Approximate relationship betweenx1,x4 and drag coefficients |
|
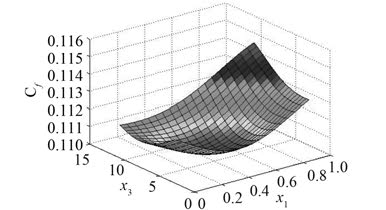
图 6 x1,x3 与潜器阻力系数的近似关系 Fig. 6 Approximate relationship betweenx1,x3 and drag coefficients |
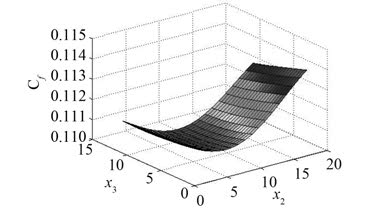
|
图 7 x2,x3 与潜器阻力系数的近似关系 Fig. 7 Approximate relationship betweenx2,x3 and drag coefficients |
粒子群算法是继遗传算法、禁忌搜索算法、模拟退火算法及蚁群优化算法后的又一种新的群智算法。PSO 通过模仿自然界中鸟类和鱼类群体觅食迁徙中,个体与群体协调一致的机理,通过群体最优方向、个体最优方向和惯性方向的协调来求解优化问题。然而,传统 PSO 在寻优过程中存在容易陷入局部极小、收敛速度慢等缺点。本文采用作者提出的改进的粒子群算法[11]进行全局最优解的搜寻。本文中潜器外形优化目标为总阻力系数最小,约束条件为头部丰满度不小于 89% 且尾部丰满度不小于 56%。改进粒子群算法优化迭代图如图 8 所示。最优结果为:
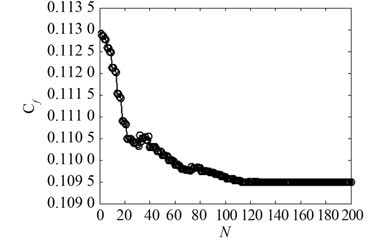
|
图 8 粒子群寻优迭代过程图 Fig. 8 Iterative process of PSO |
x1 = 0.441 6,x2 = 18.4,x3 = 7.353 2,x4 = 0.2,CR = 0.109 5。
3 结 语近似建模方法,通过采用少量的试验设计样本点来拟合输入参数与输出响应之间的关系,在优化设计过程中代替实际模型进行优化问题的分析,极大程度上减少了目标函数和约束函数评价的计算量。本文研究了基于 SVR 近似模型的潜器外形优化方法。研究内容包括拉丁超立方试验设计选取样本点、基于 ICEM 的潜器参数化建模和网格自动划分、基于 Fluent 的阻力计算及基于粒子群的潜器最小阻力外形优化。研究结果表明,基于 SVR 近似模型构建的潜器外形优化方法可以在保证获得优化方案的前提下,极大减少计算成本。
| [1] | 李冬琴, WILSONP A, 蒋志勇. 船舶操纵性能及其代理模型构建(英文)[J]. 船舶力学 , 2015, 19 (12) :1463–1474. |
| [2] | 孙丽娜, 詹成胜, 冯佰威, 等. 三体船侧体布局及型线优化设计研究[J]. 船舶工程 , 2015, 37 (5) :7–10. |
| [3] | 孙丽娜, 詹成胜, 冯佰威, 等. 三体船侧体布局及型线优化设计研究[J]. 船舶工程 , 2015, 37 (5) :7–10. |
| [4] | 常海超, 冯佰威, 刘祖源, 等. 船型优化中样本点选取方法对近似模型精度的影响研究[J]. 中国造船 , 2013, 54 (4) :84–93. |
| [5] | 程妍雪, 庞永杰, 杨卓懿, 等. 基于径向基神经网络模型的耐压壳6σ设计[J]. 上海交通大学学报 , 2014, 48 (4) :493–497. |
| [6] | AWAD M, KHANNA R. Support vector regression[M]//AWAD M, KHANNA R. Efficient learning machines:Theories, concepts, and applications for engineers and system designers. New York:Apress, 2015:67-80. |
| [7] | KAZEM A, SHARIFI E, HUSSAIN F K, et al. Support vector regression with chaos-based firefly algorithm for stock market price forecasting[J]. Applied Soft Computing , 2013, 13 (2) :947–958. DOI:10.1016/j.asoc.2012.09.024 |
| [8] | WEI Z, TAO T, DING Z S, et al. A dynamic particle filter-support vector regression method for reliability prediction[J]. Reliability Engineering&System Safety , 2013, 119 :109–116. |
| [9] | DONG H C, SONG B W, WANG P, et al. A kind of balance between exploitation and exploration on kriging for global optimization of expensive functions[J]. Journal of Mechanical Science and Technology , 2015, 29 (5) :2121–2133. DOI:10.1007/s12206-015-0434-1 |
| [10] | DONG H C, SONG B W, DONG Z M, et al. Multi-start Space Reduction (MSSR) surrogate-based global optimization method[J]. Structural and Multidisciplinary Optimization , 2016, 54 (4) :907–926. |
| [11] | 蔡厚平, 李明霞. 基于改进粒子群算法的大开口甲板板架轻量化设计[J]. 舰船科学技术 , 2015, 37 (5) :109–113. |
 2016, Vol. 38
2016, Vol. 38
