相比渐开线直齿轮,斜齿轮的重合度大,同时啮合的齿对数多,因而,斜齿轮传递动力时更加平稳,且承载能力更高,被广泛的应用在航空航天、船舶、冶金、风电等领域中。当斜齿轮运行在高速重载的工况下,会产生较大的振动和噪声,通过齿轮修形技术可以有效的降低齿轮的振动和噪声问题。
近年来,国内外学者采用各种方法,针对斜齿轮的修形技术进行广泛研究。吴永军等[1]利用接触有限元法计算了轮齿啮合线方向上的弹性变形量,作为斜齿轮齿廓修形的依据,并利用试验的方法验证了修形斜齿轮的减振效果。尚振国等[2]针对修形宽斜齿轮进行了有限元分析,研究了修形参数对轮齿齿面载荷分布和接触状态的影响。K Mao 等[3]通过非线性有限元接触分析,研究了齿面修鼓、齿顶修形和螺旋线修整对斜齿轮准静态传递误差的影响。J Bruyere 等[4]则建立了齿轮的动态分析模型,采用摄动法,确定了窄齿面斜齿轮的准静态传递误差;研究表明,斜齿轮修形后准静态传递误差有一定的减少。R Guilbault 等[5]提出利用有限条法进行仿真计算,研究了齿面修鼓和齿廓修形对斜齿轮齿面载荷分配和齿根应力的影响。P Wagaj 等[6]采用半解析半有限元的方法研究了齿廓修形对斜齿轮耐久性的影响。
目前,针对斜齿轮修形的研究主要集中在利用有限元法、有限条法等分析手段预测修形斜齿轮的准静态传递误差、齿面载荷分布和齿根应力等指标,这些手段没有考虑斜齿轮运行时的动态特性,特别是对于在高速工况下运行的斜齿轮,在修形时需要考虑其动态特性的影响;同时,一些研究建立的齿轮振动分析模型仅考虑齿轮的弯曲-扭转振动,没有综合考虑齿轮的弯曲振动、扭转振动和轴向振动的耦合影响;并且,对于高速运行下的斜齿轮,由于受到测试仪器精度的限制,采用试验测试啮合线方向振动加速度的研究很少。
基于上述问题,本文建立斜齿轮弯曲-扭转-轴向耦合振动分析模型,在模型中考虑了斜齿轮的修形参数;通过对该模型进行数值求解,得到了修形斜齿轮啮合线方向的振动加速度值;最后,建立斜齿轮振动测试功率封闭试验台,通过试验测试高速下斜齿轮啮合线振动加速度值的方法来验证振动分析模型的有效性。
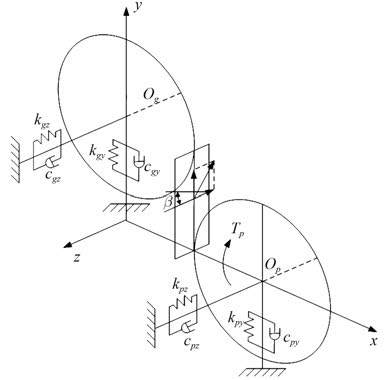
1 斜齿轮振动分析模型本节建立的斜齿轮弯曲-扭转-轴向耦合振动分析模型如图 1 所示。β 为主动齿轮螺旋角。根据几何关系,啮合点横向振动与轴向振动间的关系可用下式表示:
| $ z = y\tan \beta\text{。} $ | (1) |
|
图 1 斜齿轮弯曲-扭转-轴向耦合振动模型 Fig. 1 Bending-torsion-axial vibration model of helical gears |
不考虑齿面摩擦,系统的广义位移可表示为:
根据牛顿力学,两齿轮的动力学方程分别为:
| $ \left\{ \begin{array}{l} {m_p}{{\ddot y}_p} + {c_{py}}{{\dot y}_p} + {k_{py}}{y_p} =-{F_y}\text{,}\\ {m_p}{{\ddot z}_p} + {c_{pz}}{{\dot z}_p} + {k_{pz}}{z_p} =-{F_z}\text{,}\\ {I_p}{{\ddot \theta }_p} =-{F_y} \cdot {R_p} + {T_p}\text{。} \end{array} \right. $ | (2) |
| $ \left\{ \begin{array}{l} {m_g}{{\ddot y}_g} + {c_{gy}}{{\dot y}_g} + {k_{gy}}{y_g} = {F_y}\text{,}\\ {m_g}{{\ddot z}_g} + {c_{gz}}{{\dot z}_g} + {k_{gz}}{z_g} = {F_z}\text{,}\\ {I_g}{{\ddot \theta }_g} = {F_y} \cdot {R_g}-{T_g}\text{。} \end{array} \right. $ | (3) |
式中:下标p,g 分别为主、从动齿轮;下标y,z 分别为y 方向和z 方向;m 为齿轮的质量;I 为齿轮的转动惯量;R 为齿轮的分度圆半径;T 为齿轮的扭矩;c 为齿轮的阻尼;k 为齿轮的刚度;F 为动态啮合力。
将上式中的切向及轴向动态啮合力以参数形式(s,u)表达。并且,为了消除刚体位移,令
| $ q = {R_p}{\vartheta _p}-{R_g}{\vartheta _g}\text{,} $ | (4) |
通过联立方程(2)~(4),可以得到 5 自由度 {δ} = {ypzpygzgq}T 的动力学方程组:
| $ \left\{ \begin{aligned} & {m_p}{{\ddot y}_p} + {c_{py}}{{\dot y}_p} + {k_{py}}{y_p} + \cos \beta {c_m}({{\dot y}_p}-{{\dot y}_g} + \dot q) +\\ & \quad \quad \cos \beta {k_m}({y_p}-{y_g} + q) = {F_s} + {F_u}\text{,}\\ & {m_p}{{\ddot z}_p} + {c_{pz}}{{\dot z}_p} + {k_{pz}}{z_p} + \sin \beta {c_m}\tan \beta ({{\dot y}_p}-{{\dot y}_g} + \dot q) +\\ & \quad \quad \sin \beta {c_m}({{\dot z}_p}-{{\dot z}_g}) + \sin \beta {k_m}\tan \beta ({y_p}-{y_g} + q) +\\ & \quad \quad \sin \beta {k_m}({z_p}-{z_g}) = \tan \beta ({F_s} + {F_u})\text{,}\\ & {m_g}{{\ddot y}_g} + {c_{gy}}{{\dot y}_g} + {k_{gy}}{y_g} + \cos \beta {c_m}({{\dot y}_g}-{{\dot y}_p}-\dot q)+\\ & \quad \quad \cos \beta {k_m}({y_g}-{y_p}-q) =-{F_s}-{F_u}\text{,}\\ & {m_g}{{\ddot z}_g} + {c_{gz}}{{\dot z}_g} + {k_{gz}}{z_g}-\sin \beta {c_m}\tan \beta ({{\dot y}_p}-{{\dot y}_g} + \dot q) +\\ & \quad \quad \sin \beta {c_m}({{\dot z}_g}-{{\dot z}_p})-\sin \beta {k_m}\tan \beta ({y_p}-{y_g} + q) +\\ & \quad \quad \sin \beta {k_m}({z_g}-{z_p}) =-\tan \beta ({F_s} + {F_u})\text{,}\\ & ({m_t}\ddot q + {c_m}\cos \beta \dot q + {k_m}\cos \beta q + {c_m}\cos \beta ({{\dot y}_p}-{{\dot y}_g}) +\\ & \quad \quad {k_m}\cos \beta ({y_p}-{y_g}) = {T_p}/{R_p} + ({F_s} + {F_u})\text{。} \end{aligned} \right. $ | (5) |
式中:cm 为齿轮副法向啮合阻尼;km 为法向啮合刚度;cpy 和kpy 分别为传动轴、轴承的等效支撑阻尼和刚度,cpz 和kpz 分别为齿轮、轴的轴向等效平移振动阻尼和刚度;E为材料的弹性模量;mt 为等效质量,
本文选取 1 对未修形斜齿轮和 1 对修形斜齿轮作为计算算例,未修形主、从动斜齿轮的基本参数见表 1。其中,斜齿轮的螺旋角为 9.91°,传动比为 2.47。
|
|
表 1 斜齿轮参数 Tab.1 Parameters of helical gears |
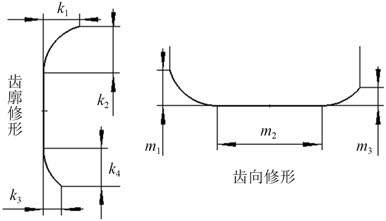
修形斜齿轮的基本参数和未修形斜齿轮基本参数一致,采用齿廓和齿向同时修形的方法,如图 2 所示。斜齿轮的齿廓修形和齿向修形的参数如表 2 所示。
|
图 2 齿廓修形和齿向修形示意图 Fig. 2 Schematic of profile modification and lead correction |
|
|
表 2 斜齿轮修形参数 Tab.2 Flank modification parameters of helical gears |
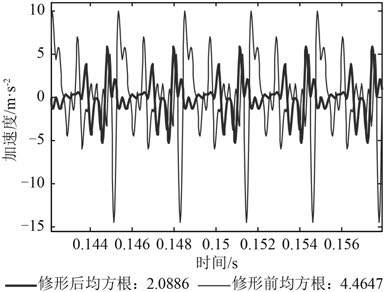
通过第 1 节建立的振动分析模型,对修形齿轮和未修形齿轮利用数值计算法进行数值求解,设定大齿轮扭矩为 865 Nm,小齿轮转速为 1 000 r/min。可以得到其啮合线方向上的振动加速度,如图 3 所示。图中发现修形前斜齿轮啮合线方向的振动加速度波动较大,振动加速度均方根值达到 4.46 m/s2;修形后,啮合线方向的振动加速度波动减小,计算得到的振动加速度均方根值较修形前降低了 53.2%。
|
图 3 修形前后斜齿轮仿真振动加速度 Fig. 3 Simulated vibration acceleration of helical gears before and after flank modification |
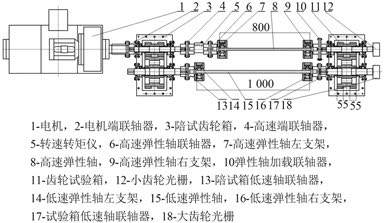
斜齿轮啮合线振动加速度测试试验台采用功率封闭结构,其组成如图 4 所示。传感器采用海德汉高速圆光栅 ROD280,其测试精度为 ± 5″;采样采用阿尔泰公司 4 通道 PCI8502H 数据采集卡,时钟频率为 40 MHz。
|
图 4 啮合线振动加速度测试试验台布置 Fig. 4 Vibration acceleration in line of action test rig arrangement |
通过高速圆光栅分别测得主动齿轮和从动齿轮的圆周角加速度
| $ \Delta \ddot x = {\ddot x_p}-{\ddot x_g} = {\ddot \varphi _p}{R_{{{bp}}}}-{\ddot \varphi _g}{R_{{{bg}}}}\text{。} $ | (6) |
式中:Rbp 和Rbg 分别为主动齿轮和从动齿轮的基圆半径。
振动加速度试验测试前,先检验修形前后斜齿轮的接触状态,来确定斜齿轮轴的安装状态。如图 5 所示,可以看到斜齿轮的接触状况良好,证明了试验安装良好,可以进行振动测试试验。

|
图 5 修形前后试验斜齿轮接触印痕 Fig. 5 Contact pattern of helical gears before and after flank modification |
设定大齿轮扭矩为 865 Nm,小齿轮转速为 1 000 r/min。通过试验测试修形和未修形斜齿轮的转角,经过信号处理后,通过式(6)计算得到修形和未修形斜齿轮的振动加速度,如图 6 所示。
|
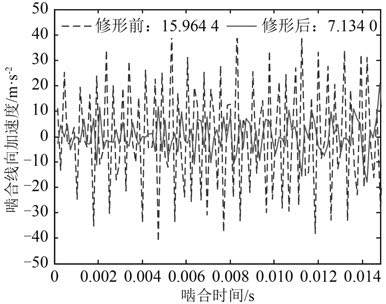
图 6 修形前后试验斜齿轮啮合线振动加速度 Fig. 6 Tested vibration acceleration in line of action of helical gears before and after modification |
可以发现,未修形试验斜齿轮的啮合线振动加速度波动较大,振动加速度均方根值为 15.96 m/s2;修形后,其波动明显减小,减小幅度为 55.3%。这个趋势和采用振动分析模型仿真计算的趋势基本一致,仿真结果减小了 53.2%。然而,仿真值和试验值两者的绝对值大小差别较大,这主要是因为,在通过振动分析模型计算时,考虑的是无安装制造误差的理想斜齿轮副;而在实际测试中,试验件由于受到加工精度、装配精度的影响,测试时会受到齿轮温升、润滑、齿面摩擦等因素的影响,试验测试值会比仿真计算值大。
4 结 语本文建立了考虑修形参数的斜齿轮弯曲-扭转-轴向耦合振动分析模型,计算了斜齿轮啮合线方向的振动加速度,并通过试验验证了该模型,得到如下的结论:
1)通过斜齿轮弯曲-扭转-轴向耦合振动分析模型进行计算,发现斜齿轮修形后,其啮合线振动加速度波动明显降低。
2)通过齿轮接触印痕试验证明了该试验件安装对中状态良好。
3)通过实验测试高速下修形斜齿轮啮合线振动加速度均方根,和仿真模型计算结果对比,发现两者修形后振动加速度均方根降低幅度基本一致,仿真结果降低了 53.2%,试验测试结果降低了 55.3%,证明了仿真模型的有效性。
| [1] |
吴勇军, 王建军, 韩勤锴, 等. 基于接触有限元分析的斜齿轮齿廓修形与实验[J]. 航空动力学报 , 2011, 26 (2) :409–415.
WU Yong-jun, WANG Jian-jun, HAN Qin-kai, et al. Tooth profile modification of helical gears and experimental study based on finite element contact analysis[J]. Journal of Aerospace Power , 2011, 26 (2) :409–415. |
| [2] |
尚振国, 王华. 宽斜齿轮修形有限元分析[J]. 农业机械学报 , 2009, 40 (2) :214–219.
SHANG Zhen-guo, WANG Hua. Finite element analysis of modified wide helical gears[J]. Transactions of the Chinese Society for Agricultural Machinery , 2009, 40 (2) :214–219. |
| [3] | MAO K. An approach for powertrain gear transmission error prediction using the non-linear finite element method[J]. Proceedings of the Institution of Mechanical Engineers, Part D:Journal of Automobile Engineering , 2006, 220 (10) :1455–1463. DOI:10.1243/09544070JAUTO251 |
| [4] | BRUYÈRE J, VELEX P. Derivation of optimum profile modifications in narrow-faced spur and helical gears using a perturbation method[J]. Journal of Mechanical Design , 2013, 135 (7) :071009. DOI:10.1115/1.4024374 |
| [5] | GUILBAULT R, GOSSELIN C, CLOUTIER L. Helical gears, effects of tooth deviations and tooth modifications on load sharing and fillet stresses[J]. Journal of Mechanical Design , 2006, 128 (2) :444–456. DOI:10.1115/1.2167650 |
| [6] | WAGAJ P, KAHRAMAN A. Influence of tooth profile modification on helical gear durability[J]. Journal of Mechanical Design , 2002, 124 (3) :501–510. DOI:10.1115/1.1485289 |
 2016, Vol. 38
2016, Vol. 38
