可倾瓦径向滑动轴承已经普遍应用于大型回转机械,经常运行于负荷较轻、高速等工况条件下[1-3]。可倾瓦轴承结构研究已有很多论文或专利文献发表,目前对于可倾瓦轴承的研究主要集中在特殊工况和对其支撑的转子动力学的研究[4-7]。针对高工况半速机、大型水轮发电机组等这类重载设备,其运行特点在于轴承轴颈几何尺寸很大、径向负荷较大、转速较低且工作偏心率较大,如何实现该类设备用可倾瓦轴承的润滑动力膜,是这类轴承研究的一个非常重要方面[2,6,8]。本文提出的非均布变包角可倾瓦轴承是指比一般轴承瓦块支点位置、包角设计固定不同,采取变化的包角设计思路、选择有较短长度的瓦面型线和不同支点位置的可倾瓦轴承。对于径向滑动轴承来说,如果采用的轴承瓦块瓦面型线为变包角短程型线,那么将会给轴承瓦块的周向空间位置分布、可倾瓦支点位置分布带来结构上的灵活性;将会使得润滑油运行历程变短继而影响油膜压力的分布情况、温度场分布情况、润滑油粘性或剪切耗散程度及轴承功耗、包括压缩变形或弯曲变形在内的瓦块弹性变形、瓦块热变形等[9]。此外,非均布变包角概念的提出,也为新结构轴承的设计带来可行性。基于此,本文提出并进行非均布瓦包角可倾瓦轴承研究,在给出此类可倾瓦轴承结构形式的基础上,将详细分析轴承动力润滑特性,包括建立考虑瓦块支点位置、油膜温粘效应、热弹变形等对轴承性能求解数学模型和实例分析。
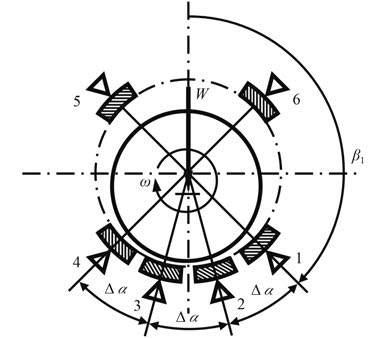
1 非均布变包角径向可倾瓦轴承润滑模型图 1 所示为非均布变包角径向可倾瓦轴承。这是一种采用较传统可倾瓦包角小的、且瓦块支点可密集布置于轴颈下方或载荷相对一方的一种轴承结构形式。对于大型低速重载轴承来说,其轴颈的几何尺寸比较大及转速较低,从考虑轴承制造、安装、承载能力、功耗和抵抗变形能力等出发,采用这种结构型式能否达到特定的润滑性能要求,还需要对它进行深入的研究分析,为正确设计和应用非均布变包角可倾瓦轴承奠定了理论基础。
|
图 1 非均布变包角可倾瓦轴承结构形式 Fig. 1 The structure of non-uniform change pad-angle tilting-pad bearing |
|
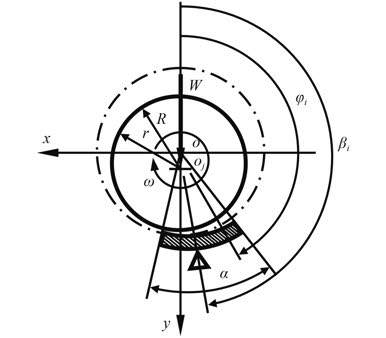
图 2 可倾瓦轴承坐标示意图 Fig. 2 ThePlotter ofTilting-pad bearing |
图 2 为可倾瓦轴承坐标示意图,考虑轴承瓦块弹性变形与热变形后的无量纲油膜厚度方程为[9]:
| $H = {H_0} + {{\pi}} \left( {{\varphi _i},{\lambda _i}} \right) + \vartheta \left( {{\varphi _i},{\lambda _i}} \right)\text{,}$ | (1) |
| $\begin{aligned} {H_0} = & 1-{\nu _i}\cos \left( {{\beta _i}-{\varphi _i}} \right) + {\varepsilon _i}\cos \left( {{\varphi _i}-\theta } \right)+\\ & {\delta _i}\sin \left( {{\beta _i}-{\varphi _i}} \right)\psi \text{。}\end{aligned}$ | (2) |
式中,H0 为不考虑瓦块弹性或热弹变形时无量纲油膜厚度,H0 =h0/c,c为轴承半径间隙;(φi,λi)为由油膜压力引起的无量纲瓦块内表面径向弹性位移;
对于图 2 所示的径向滑动轴承,假设润滑油为不可压缩牛顿流体、稳态层流流动且无滑移,其彻体力和惯性力忽略不计,润滑油的物性参数为常量,则油膜压力分布可由如下形式的雷诺方程表示[10]:
| $\frac{1}{{{r^2}}}\frac{\partial }{{\partial \phi }}(\frac{{{h^3}}}{{12\mu }}\frac{{\partial p}}{{\partial \phi }}) + \frac{\partial }{{\partial z}}(\frac{{{h^3}}}{{12\mu }}\frac{{\partial p}}{{\partial z}}) = \frac{\omega }{2}\frac{{\partial h}}{{\partial \phi }} + \frac{{\partial h}}{{\partial t}}{\text {。}}$ | (3) |
式中,p 为油膜压力;μ 为润滑油的动力粘度;ω 为轴承轴颈的转动角速度;t 为时间变量;z 为轴承瓦块瓦面上任意点的轴向坐标。
无量纲雷诺方程为:
| $\frac{\partial }{{\partial \phi }}\left( {\frac{{{H^3}}}{{\bar \mu }}\frac{{\partial P}}{{\partial \phi }}} \right) + {\left( {\frac{D}{L}} \right)^2}\frac{\partial }{{\partial \lambda }}\left( {\frac{{{H^3}}}{{\bar \mu }}\frac{{\partial P}}{{\partial \lambda }}} \right) = 3\frac{{\partial H}}{{\partial \phi }} + 6\frac{{\partial H}}{{\partial \tau }}{\text{。}}$ | (4) |
式(4)满足 Reynolds 边界条件和补充条件:在两侧边,λ = ± 1,P = 0;在进油边,φ =φi1,P =P0;在出油边Γa 上,φ =φi2,P = 0;在油膜破裂边Γb 上,φ =φib,
根据热力学第一定律,可得以油膜压力形式表示的油膜能量方程[11]:
| $\begin{aligned} & \left. {\rho {c_v}\left[ {\left( {\frac{{\omega rh}}{2}-\frac{{{h^3}}}{{12\mu r}}\frac{{\partial p}}{{\partial \phi }}} \right)} \right]\frac{1}{r}\frac{{\partial T}}{{\partial \phi }}-\frac{{{h^3}}}{{12\mu }}\frac{{\partial p}}{{\partial z}}\frac{{\partial T}}{{\partial z}}} \right]= \\ & \quad \frac{{\mu {r^2}{\omega ^2}}}{h} + \frac{{{h^3}}}{{12\mu }}\left[ {{{\left( {\frac{1}{r}\frac{{\partial p}}{{\partial \phi }}} \right)}^2} + {{\left( {\frac{{\partial p}}{{\partial z}}} \right)}^2}} \right]-{k_t}\left( {T-{T_s}} \right){\text{。}} \end{aligned}$ | (5) |
式中,T 为油膜温度;ρ 为润滑油密度;cv 为润滑油比热;kt 为轴承流体—固体分界面处的传热系数;Ts 为轴承瓦体表面上的温度。
无量纲能量方程为:
| $\begin{aligned} & \left( {H-\frac{1}{6}\frac{{{H^3}}}{{\bar \mu }}\frac{{\partial P}}{{\partial \phi }}} \right)\frac{{\partial \bar T}}{{\partial \phi }}-\frac{1}{6}{\left( {\frac{D}{L}} \right)^2}\frac{{{H^3}}}{{\bar \mu }}\frac{{\partial P}}{{\partial \lambda }}\frac{{\partial \bar T}}{{\partial \lambda }}= \\ & \!\!{T_c}\frac{{\bar \mu }}{H}\left\{ {1\!\! +\!\! \frac{{{H^4}}}{{12。{{\bar \mu }^2}}}\left[ {{{\left( {\frac{{\partial P}}{{\partial \phi }}} \right)}^2}\!\! +\!\! {{\left( {\frac{D}{L}} \right)}^2}{{\left( {\frac{{\partial P}}{{\partial \lambda }}} \right)}^2}} \right]} \right\} \!-\! {T_d}\left( {\bar T \!-\! {{\bar T}_s}} \right){\text{,}}\!\!\! \end{aligned}$ | (6) |
式中:
本文采用 Walther 的粘度温度关系式[12]:
| ${\rm{lglg}}\left( {\gamma + \alpha } \right){\rm{ }} = C-D{\rm{lg}}{K_t}\text{,}$ | (7) |
式中:γ 为润滑油运动粘度,γ =μ/ρ;α,C,D 为与润滑油种类有关的常数;Tk 为润滑油的绝对温度,Tk = 273.15 +T。
1.5 瓦块热传导方程及其无量纲方程当瓦体导热时,对于域内无热源且瓦体的物性参数为常量的稳态瓦体温度场分布可用如柱坐标形式的热传导方程表示[9]:
| $\frac{{{\partial ^2}{T_b}}}{{\partial r_b^2}} + \frac{1}{{{r_b}}}\frac{{\partial {T_b}}}{{\partial {r_b}}} + \frac{1}{{r_b^2}}\frac{{{\partial ^2}{T_b}}}{{\partial {\phi ^2}}} + \frac{{{\partial ^2}{T_b}}}{{\partial {z^2}}} = 0\text{,}$ | (8) |
式中:
无量纲传热方程为:
| $\frac{{{\partial ^2}{{\bar T}_b}}}{{\partial {{\bar r}^2}}} + \frac{1}{{\bar r}}\frac{{\partial {{\bar T}_b}}}{{\partial \bar r}} + \frac{1}{{{{\bar r}^2}}}\frac{{{\partial ^2}{{\bar T}_b}}}{{\partial {\phi ^2}}} + {\left( {\frac{D}{L}} \right)^2}\frac{{{\partial ^2}{{\bar T}_b}}}{{\partial {\lambda ^2}}} = 0\text{,}$ | (9) |
式中:
式(9)满足如下边界条件为[8]:
瓦块工作表面
| $\frac{{\partial {{\bar T}_b}}}{{\partial \bar r}}\left| {_{\bar r = 1}} \right. =-\frac{{{\kappa _1}}}{{{k_{exc}}}}R({\bar T_b}\left| {_{\bar r = 1}} \right.-\bar T)\text{,}$ |
瓦进油边界面
| $\frac{{\partial {{\bar T}_b}}}{{\partial \bar r}}\left| {_{\phi = {\phi _1}}} \right. =-\frac{{{\kappa _2}}}{{{k_{exc}}}}R\left( {{{\bar T}_b}\left| {_{\phi = {\phi _1}}} \right.-{{\bar T}_{bath}}} \right)\text{,} $ |
瓦出油边界面
| $\frac{{\partial {{\bar T}_b}}}{{\partial \bar r}}\left| {_{\phi = {\phi _2}}} \right. =-\frac{{{\kappa _3}}}{{{k_{exc}}}}R({\bar T_b}\left| {_{\phi = {\phi _2}}} \right.-{\bar T_{bath}})\text{,} $ |
对称面的边条
瓦侧边处界面
| $\frac{{\partial {{\bar T}_b}}}{{\partial \lambda }}\left| {_{\lambda = 1}} \right. =-\frac{{{\kappa _4}}}{{{k_{exc}}}}R({\bar T_b}\left| {_{\lambda = 1}} \right.-{\bar T_{bath}})\text{,} $ |
瓦背界面边条
| $\frac{{\partial {{\bar T}_b}}}{{\partial \bar r}}\left| {_{\bar r = {{\bar R}_{ep}}}} \right. =-\frac{{{\kappa _5}}}{{{k_{exc}}}}R({\bar T_b}\left| {_{\bar r = {{\bar R}_{ep}}}} \right.-{\bar T_{bath}})\text{,}$ |
式中:κi (i = 1~5)为对流换热系数;kexc 为瓦体的导热系数;
当不计各部分摩擦阻力和瓦块自重引起力矩时,瓦块的力矩平衡方程为:
| ${M_i} = \int_{-L/2}^{{\kern 1pt} L/2} {\int_{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\phi _{{\rm{i}}2}}}^{{\kern 1pt} {\kern 1pt} {\phi _{{\rm{i}}1}}} {p\sin ({\beta _i}-{\phi _i})} } {r^2}{\rm d}\phi {\rm d}z = 0\text{,}$ | (10) |
无量纲方程为:
| $\begin{aligned} {{\bar M}_i} =& \int_{-1}^{ 1} {\int_{{\phi _{i2}}}^{{\phi _{i1}}} {P\sin ({\beta _i}-{\phi _i})} } {\rm d}\phi {\rm d}\lambda= \\ & {M_i}/({\mu _0}\omega {r^2}L{\psi ^{-2}}) = 0 \text{。}\end{aligned}$ | (11) |
整个计算过程采用有限差分法和有限元相结合的方法实现,联立求解上述润滑分析式(1)~式(11),其具体的实现步骤为:
1)输入轴承结构的基本尺寸及运行工作参数;
2)对压力与温度求解区域进行有限差分网格划分,并确定差分网格节点坐标及有限元节点信息;
3)利用式(1)和式(2),根据给定偏心率ε0、轴承偏位角θ0 及瓦块摆角δ0 计算油膜厚度H;
4)初定油膜温度场,计算出油膜中各节点的粘度值;
5)求解雷诺方程式(3)获得压力分布;
6)初定瓦块瓦面温度分布,由解能量方程式(5)确定油膜温度分布;
7)判断温度是否满足收敛要求,重复步骤 4~步骤 6 过程,直至满足精度为止;
8)计算力矩,确定瓦块摆角,重复步骤 3~步骤 8 过程使得力矩满足一定的精度;
9)求承载能力,修正偏位角,重复步骤 3~步骤 9 过程直至满足载荷精度为止;
10)计算轴承静特性,包括无量纲最小油膜厚度Hmin、载荷系数ζ、流量、摩擦阻力系数、功耗等性能参数;
11)分别取位移与速度的小扰动,计算轴承的动力特性系数;
12)输出结果,并结束。
2 算例分析本文对一类六瓦非均布变包角径向可倾瓦轴承进行分析(结构如图 1 所示,图中β1 为标定第 1 块瓦支点角坐标;Δα 为支点间夹角),其长径比L/D 为 0.40,β1 = 135°,瓦包角α 为 22.5°,支点间夹角 Δα 分别为 30°,40°和 50°,转速为 100 r/min。本节主要分析该六瓦非均布变包角可倾瓦轴承支点位置分布和瓦块包角大小对轴承热弹流体动力润滑性能影响情况;限于篇幅本文只给出其对承载能力和油膜压力分布的影响结果。
2.1 瓦块支点位置分布对轴承性能影响1)承载能力
图 3 为不同支点间夹角 Δα 下轴承无量纲最小油膜厚Hmin 度随无量纲载荷系数ζ(=

|
图 3 最小油膜厚度随承载系数的变化关系 Fig. 3 The variation between minimum film thickness and load coefficient |
2)油膜压力分布
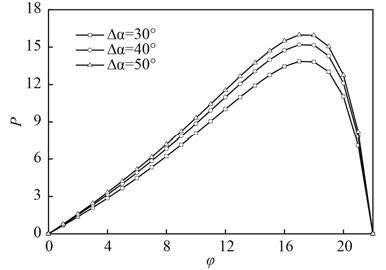
图 4 为轴承在同一承载系数ζ = 3.957 下主承载瓦 2 的无量纲周向油膜压力分布曲线。可见,随着小包角瓦块支点间夹角 Δα 减小,即支点的密集布置程度的提高,降低了主承载瓦 2 瓦面上的最大油膜压力P2max。当支点间夹角 Δα 为 30°时,瓦 2 瓦面最大油膜压力P2max 为 13.858 6,这比支点间夹角 Δα 为 40°(15.194 7)和 50°(15.980 7)时降低了 8.79% 和 13.28%。可见瓦块支点位置的改变对油膜压力分布有一定的影响,从而会引起轴承载荷的变化。
|
图 4 瓦 2 瓦周向油膜压力分布 Fig. 4 The circumferential film pressure distribution on Pad 2# |
图 5 为轴承在同一承载系数ζ = 3.957 下侧瓦 1 的无量纲周向油膜压力分布。与主承载瓦 2 相反,支点间夹角 Δα 的减小使得侧瓦 1 的油膜压力增加。当 Δα 为 30°时,最大油膜压力 P1max 为 2.477 7,比支间点间夹角 Δα 为 40°(1.198 4)和 50°(0.618 8)时的分别增大了 106.75% 和 300.40%。降低最大承载瓦 2 和提高下方侧瓦 1 的油膜压力有利于轴承各瓦承载均衡。

|
图 5 瓦 1 瓦面上的油膜压力分布 Fig. 5 The film pressure distribution on Pad 1# |

|
图 6 载荷系数随偏心率的变化关系 Fig. 6 The variation between load coefficient and eccentricity ratio |
本节采用对称布置且下方为二瓦及包角αt = 45°和四瓦及包角αt = 22.5°,并且位于下方瓦间间隙角αc = 8°的情况来研究瓦块包角大小对轴承热弹流体动力润滑性能的影响。
1)载荷系数与轴颈偏心率
图 6 为载荷系数随偏心率的变化曲线。在同一偏心率ε 下,采用较小包角瓦块的轴承载荷系数ζ 比采用较大包角的大,且随着偏心率的增大,两者具有较大的差别。当偏心率ε 为 0.800 时,包角αt 为 22.5°和 45°时所对应的载荷系数ζ 分别为 3.589 9 和 1.011 0;当偏心率ε 为 0.910 时,包角αt 为 22.5°和 45°时的所对应的载荷系数ζ 分别为 9.038 6 和 2.213 4。如要达到相近载荷系数就需要大包角的轴承具有较大的偏心率,那么这很容易导致轴瓦温升的进一步增大。
2)承载能力及最小油膜厚度
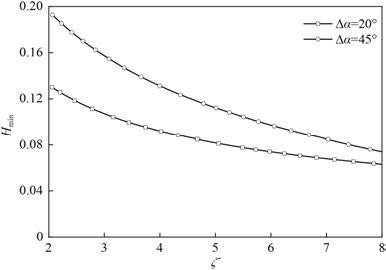
图 7 为无量纲最小油膜厚度随载荷系数的变化曲线。载荷系数ζ 在 2.0 到 8.0 时,具有小包角瓦块轴承的最小油膜厚度Hmin 比采用较大包角的小。随着载荷系数ζ 的增大,两者相差越来越小。载荷系数ζ 为 3.957 时,小包角可倾瓦轴承的最小油膜厚度Hmin 为 0.092 5;比较大包角(0.134)可倾瓦轴承的要小 30.97%;载荷系数ζ 为 7.852 时,小包角可倾瓦轴承的最小油膜厚度Hmin 为 0.063 6,比较大包角(0.074 4)可倾瓦轴承的要小 14.52%。
|
图 7 最小油膜厚度随载荷系数的变化关系 Fig. 7 The variation between minimum film thickness and load coefficient |

|
图 8 周向油膜压力的分布曲线 Fig. 8 The circumferential film pressure distribution curves |
3)压力分布
图 8为载荷系数ζ 为 7.852 时无量纲周向油膜压力分布。由于结构上的灵活性、瓦块密集布置、瓦块抗变形能力增强使得小包角瓦块结构轴承在同样承载条件下降低了最大油膜压力及瓦面温度。根据计算,瓦块包角αt 为 22.5°时的最大油膜压力发生在φ = 17°,其压力值为P2max = 17.327 6,这比αt 为 45°时且最大压力位于φ = 24.58°(22.276 1)的降低了 22.21%。
3 结 语1)提出了非均布变包角可倾瓦轴承结构,并构建了非均布变包角径向可倾瓦轴承的流体动力润滑模型,包括轴承油膜厚度方程、Reynolds 方程、能量方程、粘温方程以及瓦块热传导方程和瓦块力矩平衡方程。
2)采用数值方法,求解获得了一组非均布变包角径向可倾瓦轴承的静态特性,以此分析了瓦块支点位置分布和瓦块包角大小对轴承润滑性能影响。
3)研究结果表明瓦块支点位置的改变对油膜压力分布有一定的影响,轴承在较小的支点夹角下承载能力较高;小包角的可倾瓦轴承的最小油膜厚度较小,但油膜压力的最大值会有所降低。
| [1] |
刘宏, 宫晓春, 王晋麟. 基于主动润滑可倾瓦轴承转子系统的振动主动控制[J]. 强度与环境 , 2011, 38 (5) :8–17.
LIU Hong, GONG Xiao-chun, WANG Jin-lin. Vibration active control of tilting pad journal bearing rotor system based on the active lubrication[J]. Structure & Environment Engineering , 2011, 38 (5) :8–17. |
| [2] | YAN Z Y, WANG L P, QIAO G, et al. An analytical model for complete dynamical coefficients of a tilting-pad journal bearing[J]. Tribology International , 2010, 43 (1/2) :7–15. |
| [3] |
吕延军, 张永芳, 季丽芳, 等. 可倾瓦轴承-转子系统非线性动力行为[J]. 振动、测试与诊断 , 2010, 30 (5) :539–543.
LV Yan-jun, ZHANG Yong-fang, JI Li-fang, et al. Analysis of nonlinear dynamic behaviors of rotor system supported by tilting-pad journal bearings[J]. Journal of Vibration, Measurement & Diagnosis , 2010, 30 (5) :539–543. |
| [4] |
王丽萍, 乔广, 郑铁生. 可倾瓦轴承的完整动力分析模型及计算方法[J]. 机械工程学报 , 2008, 44 (1) :75–80.
WANG Li-ping, QIAO Guang, ZHENG Tie-sheng. Analysis and calculate model for the complete dynamical coefficients of tilting-pad bearings[J]. Chinese Journal of Mechanical Engineering , 2008, 44 (1) :75–80. DOI:10.3901/JME.2008.01.075 |
| [5] |
杨玉敏, 戴旭东, 马玥珺, 等. 考虑轴颈与轴瓦耦合运动的可倾瓦轴承完整动力学模型的研究[J]. 润滑与密封 , 2010, 35 (6) :45–49.
YANG Yu-min, DAI Xu-dong, MA Yue-jun, et al. Research on the full dynamical model of tilting-pad journal considering the coupling moving of shaft and pads[J]. Lubrication Engineering , 2010, 35 (6) :45–49. |
| [6] | ABU-MAHFOUZ I, ADAMS M L. Numerical study of some nonlinear dynamics of a rotor supported on a three-pad tilting pad journal bearing (TPJB)[J]. Journal of Vibration and Acoustics , 2005, 127 (3) :262–272. DOI:10.1115/1.1888593 |
| [7] |
王永亮, 刘占生, 钱大帅. 可倾瓦轴承瓦块摆动特性[J]. 哈尔滨工业大学学报 , 2011, 43 (9) :62–66.
WANG Yong-liang, LIU Zhan-sheng, QIAN Da-shuai. Swing characteristic of pads in tilting pad bearing[J]. Journal of Harbin Institute of Technology , 2011, 43 (9) :62–66. |
| [8] | DESBORDES H, FILLON M, FRÊNE J, et al. The effects of three-dimensional pad deformations on tilting-pad journal bearings under dynamic loading[J]. Journal of Tribology , 1995, 117 (3) :379–384. DOI:10.1115/1.2831262 |
| [9] | 朱均, 虞烈. 流体润滑理论[M]. 西安: 西安交通大学出版社, 1991 . |
| [10] | 张直明, 张言羊, 谢友柏, 等. 滑动轴承的流体动力润滑理论[M]. 北京: 高等教育出版社, 1986 . |
| [11] | PINKUS O, STERNLICHT B. Theory of hydrodynamic lubrication[M]. New York: McGraw-Hill, 1961 . |
| [12] | 孙大成. 润滑力学讲义[M]. 北京: 中国友谊出版社, 1991 . |
 2016, Vol. 38
2016, Vol. 38
