船舶在风浪中航行,会受到风浪流的影响,因而船舶将会产生各种摇荡运动,船舶的六自由度运动中,横摇对船舶的运动安全影响最大,较大幅度的横摇会产生很多不良影响,尤其是风浪中大幅度的横摇有可能会导致船舶倾覆,从而引发海难事故的发生。能精确高效地预测船舶横摇状态对于保证人员、船舶以及货物安全有着非常重要的实践应用意义。然而由于船舶的摇荡运动[1-2]具有非平稳性、非线性等特点,使用传统的静态线性预测模型对船舶横摇状态进行实时预报,一般难以得到比较实用的的结果,很多文献[3-4]也论证了这一点。近年来,蓬勃发展的人工神经网络,其较强的非线性映射和自学习自适应能力使得其在工程计算领域得到了广泛的应用。因而人工神经网络能够进行复杂的、非线性的、非平稳性的系统仿真预测,BP 神经网络(Back Propagation,BP)是一种多层前馈神经网络,是当今最常用的一种神经网络模型。然而,BP 神经网络本身尚有一些缺陷[5-6]:网络模型参数的选择随机性比较大;优化过程可能陷入局部最优;对网络参数的选择比较敏感,训练的收敛速度相对较难控制等。研究者将粒子群优化算法与 BP 网络结合起来[7],以改进 BP 网络的非线性映射能力,但仍易出现早熟收敛,搜索效率较低等现象。而加入自适应变异算子的粒子群优化算法(self-adapting particle swarm optimization algorithm,SAPSO)结合了 PSO 算法的全局搜索寻优能力和自适应变异算法的跳出局部最优解的能力,使得 BP 网络模型能够迅速跳出局部最优并能快速找到全局最优解。本文使用自适应粒子群优化算法建立 SAPSO-BP 混合预报模型,采用该混合预报模型对船舶横摇运动状态进行实时预测[8],经仿真试验训练,与传统单一的 BP 网络预测模型进行对比,可以得出结论:SAPSO-BP 预测模型具有更精确的预测结果。
1 船舶横摇运动根据 Conolly 理论分析,得出船舶在波浪中的横摇运动方程式:
| $ {I'}_{xx}\ddot \varphi + 2N\dot \varphi + Dh\varphi = Dh{a_m}\sin \omega t{\text{。}} $ | (1) |
式中:2N 为船舶的横摇阻尼力矩的比例系数;D 为船舶的排水量;h 为船舶的横稳心高度;φ,
使用不同的推导方法可以导出不同的预测模型。首先t 时刻的船舶横摇角度φt 可由方程
| $ {\varphi _t} = f({\varphi _{t-1}},{\varphi _{t-2}}){\text{。}} $ | (2) |
此非线性方程式表明,船舶在不同时刻的横摇角度值可以由船舶的横摇时间序列进行预测。
2 SAPSO-BP 算法的实现 2.1 BP 神经网络算法BP 算法本质是将样本仿真的输入输出映射为非线性优化问题,也就是将网络的连接权值作为变量,将网络训练的误差函数作为目标函数的多元变量求极值问题,传统的 BP 网络模型通常由输入层、输出层和隐含层 3 层构成,网络的仿真实验使用选定的训练样本进行学习训练,从而确定训练模型的模型参数。BP 网络模型仿真训练过程包括输入信息正向传播和误差信息反向传播,在一定的迭代循环条件下,2 个过程反复执行,直到模型结果收敛。输入数据经输入层进入隐含层,经隐含层节点激活函数计算进入输出层,得到正向传播结果。网络模型的第j 个神经元的输出可表示为:
| $ y_j^k = \left( {f\sum\limits_{i = 1}^{k-1} {w_{ij}^{k-1}y_j^{k-1}-\theta _j^k} } \right){\text{。}} $ | (3) |
式中:j = 1,2,…,n,k = 1,2,…,m;f(x)为隐含层的激活函数;
| $ w(k + 1) = w(k)-\eta \partial E/\partial W(k) + \alpha \Delta w(k){\text{。}} $ | (4) |
式中:η 为学习效率;α 为动量项系数。
网络模型使用训练样本进行学习训练,使得模型的权值阈值与训练样本之间匹配,经误差信息反向传播调整后的权值阈值也为非线性函数的隐含形式。经过一定次数的迭代仿真训练学习得到与样本匹配的网络模型即可用于进行预测。BP 网络具有很好的非线性映射能力,但收敛速度较慢,如果初始的网络参数选择不当,BP 模型的仿真训练将会陷入局部最优;
2.2 粒子群优化算法粒子群优化算法(particle swarm optimization,PSO)[9]的理论源于对鸟群捕食的行为研究:鸟群在寻找食物的过程中,每只鸟通过搜寻当前距离食物最近的鸟的周围高效地获取食物。PSO 算法便是从鸟群捕食行为中获得启发而产生的。PSO 求解时,问题的解就是种群空间中每只鸟的位置,每只鸟称为一个“粒子”。首先随机初始化一群粒子(随机解),每个粒子在搜寻空间中初始化自己位置和速度,且每个粒子都有一个适应度函数值,适应度函数由所优化的问题决定。每一次迭代循环过程中,每个粒子以一定的速度通过跟踪个体极值和群体极值来更新自身的位置,个体极值是粒子在寻优过程中自身所寻找到的最优值,而群体极值则是整个种群在寻优过程中获得的最优值(也称为全局最优值)。
设搜寻空间中有d 个粒子,其中第i 个粒子可用一个D 维向量表示,第i 个粒子的位置表示为Xi =(Xi1,Xi2,…,XiD),i = 1,2,…,d,速度为Vi = (Vi1,Vi2,…,ViD) 。记第i 个粒子搜索到的最优位置为Pi =(Pi1,Pi2,…,PiD),整个粒子群搜索到的最优位置为Pg =(Pg1,Pg2,…,PgD)。粒子状态更新操作如下:
| $ {V_{{i_d}}} = w{V_{{i_d}}} + {c_1}{r_1}({P_{{i_d}}}-{X_{{i_d}}}) + {c_2}r{}_2({P_{{g_d}}}-{X_{{i_d}}}){\text{,}} $ | (5) |
| $ {X_{{i_d}}} = {X_{{i_d}}} + {V_{{i_d}}}{\text{。}} $ | (6) |
式中,i = 1,2,…,m,d = 1,2,…,D;w 为惯性因子;学习因子c1 和c2 是非负常数,通常c1 =c2 = 2;r1 和r2 为介于 [0,1] 之间的随机数。
PSO 优化算法是一种全局迭代寻优的工具,寻优开始时,算法将每个粒子初始化为一组初始随机解,根据优化问题选择适应度函数,设定迭代寻优次数,根据适应度函数计算每个粒子的适应度值从而进行迭代寻优,搜寻到最优粒子(即最优解)。
2.3 SAPSO 优化算法PSO 算法的寻优收敛速度较快,但也存在着在寻优过程中容易早熟收敛、搜索准确度低、循环后期迭代效率较低等缺点。仿照遗传算法(Genetic Algorithm,GA)中的变异操作,在 PSO 算法中加入变异算子,对初始随机变量再一次重新随机初始化。引入的变异算子将初始随机变量再次随机初始化,扩展了在寻优中不断缩小的种群搜寻空间,使得已寻优得到的粒子跳出之前寻优得到最优位置,从而在更大的搜寻空间中进行迭代寻优,增加了算法寻找到更优值的概率。因此,在传统 PSO 算法的基础上加入变异算子,实质就是在每次粒子迭代更新之后,将迭代更新后的粒子再以一定的概率随机初始化。其中自适应变异算子公式为:
| $ pop(j,pos) = \lambda \times rands(1,1){\text{,}}\;\;{\text{if}}\;\;rand > c{\text{。}} $ | (7) |
式中:j 为粒子种群规模;pos 为一个离散的均匀随机正整数;λ 为粒子种群位置最大值;C 为一个正的常数,通常小于 1。
种群迭代进化过程中最优个体适应度函数值变化如图 1 所示。由图可知,SAPSO-BP 混合预测模型的适应度函数值明显小于 PSO-BP 模型,而且其误差递减速率更快。也就是说,SAPSO-BP 模型可以自适应的跳出局部极小值点并能快速的搜索到一个更优的结果。其中适应度函数的方程如下:

|
图 1 SAPSO-BP 模型和 PSO-BP 模型之间的适应度函数曲线比较 Fig. 1 The comparison of fitness function curve between SAPSO-BP model and PSO-BP model |
| $ error = \left| {{Y_k}-{O_k}} \right|{\text{。}} $ | (8) |
式中,Yk 为网络模型的预测输出值;Ok 为网络模型的实际输出值。
2.4 SAPSO 优化算法训练 BP 神经网络采用 SAPSO 算法对 BP 神经网络模型的权值和阈值进行优化,以提高神经网络预测模型的收敛性。将整个网络预测模型设置为 5 个输入节点,1 个输出节点。该算法的实现步骤如下:
1)载入并初始化船舶的实测横摇数据,创建 BP 神经网络并设置 SAPSO 算法的参数:c1 = 1.5,c2 = 1.494 45,种群迭代次数为 100,种群规模数量为 10。并将每个粒子的速度和位置进行限定。
2)将 BP 神经网络的权值和阈值作为 SAPSO 算法的粒子种群位置进行随机初始化,根据选定的适应度函数计算每 1 个粒子种群的适应度函数值。
3)通过方程(5)和(6)更新每个粒子的速度和位置,然后计算粒子更新之后的适应度函数值并通过方程(7)更新粒子搜寻到的个体最优值Pi 和全局最优值Pg。
4)判断每个粒子的适应度函数值是否满足误差要求,或者算法是否达到最大迭代次数。如果满足要求,算法执行下一步,否则将返回上一步继续迭代循环寻优。
5)结束 SAPSO 算法的迭代寻优,进而将算法寻优得到的最优权值阈值赋给 BP 神经网络以便行仿真实验。
6)BP 神经网络模型的参数设置如下:迭代次数为 100,学习率为 0.1,训练目标为 0.000 01。然后将 SAPSO 优化算法寻优得到的权值和阈值赋给 BP 神经网络进行船舶横摇运动预测仿真。
3 仿真结果与讨论 3.1 BP,SAPSO-BP 模型的仿真实验在本项研究中,均方根误差(root mean square error,RMSE)用来计算不同预测模型的精确度,RMSE 公式为:
| $ RMSE = \sqrt {\frac{{\sum\limits_{k = 1}^n {{{\left( {{y_k}-{{\hat y}_k}} \right)}^2}} }}{N}} {\text{。}} $ | (9) |
式中:n 为预测数据的个数;yk 为实测船舶横摇数据;
本文所使用的船舶横摇[10]数据均来自于“育鲲”轮的海上直航实验。“育鲲”轮是 1 艘隶属于大连海事大学的现代化科研教学实习船,“育鲲”轮的船舶参数如表 1 所示。舰船航向、航速、位置、横摇及纵摇等航行信息都由船舶的航行记录仪 VDR(Voyage Data Record,VDR)进行记录。从“育鲲”轮的 VDR 中选取一定周期的实测横摇数据进行仿真实验。数据的采样时间为等间隔采样,采样间隔均为 1 s,总共选取 1 500 组横摇数据。仿真实验为单步仿真,在试验中,所选数据的前 1 000 组数据用于网络模型的训练学习,剩余的 500 组数据用于网络模型的预测输出。
|
|
表 1 育鲲轮船舶参数 Tab.1 Ship parameters of Yukun |
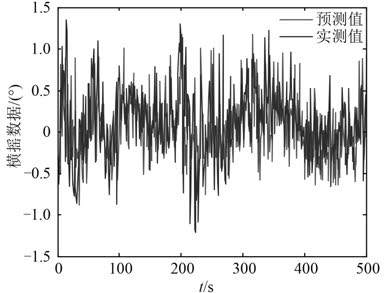
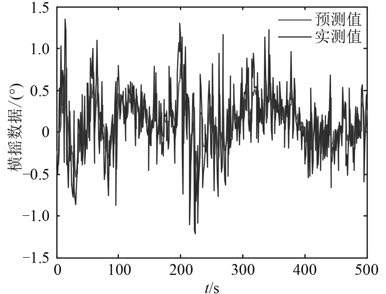
图 2和图 3 分别为 BP 网络模型,SAPSO-BP 网络模型的预测结果与实测结果的对比图。从图中可看出,SAPSO-BP 混合预测模型的预测结果比传统的 BP 网络模型预测结果要好,且当船舶的横摇角度在短时间内急剧变化时,SAPSO-BP 预测模型相也有着更好的自我辨识、自我适应和自我纠错能力。图 4 同时表明 SAPSO-BP 模型有着瞬间修正较大预测误差的能力。
|
图 2 BP 网络模型的仿真实验结果 Fig. 2 Simulation results of BP network model |
|
图 3 SAPSO-BP 网络模型的仿真实验结果 Fig. 3 Simulation results of SAPSO-BP network model |

|
图 4 BP 网络模型的预测误差曲线 Fig. 4 Prediction error curve of BP network model |
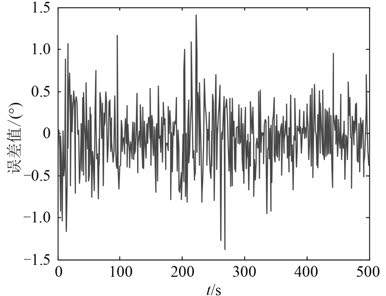
为了更准确描述 2 种模型的预测结果以及模型的不同之处,将传统的 BP 预测模型与改进的自适应变异 PSO-BP 预测模型的船舶横摇实时预测误差进行比较,其误差曲线图如图 4 和图 5 所示。
|
图 5 SAPSO-BP 网络模型的预测误差曲线 Fig. 5 Prediction error curve of SAPSO-BP network model |
通过对比图 4 和图 5可分析出:传统的 BP 网络模型的预测误差变动幅度较大,而且误差数值的变化也比较明显,当船舶横摇角度发生急剧变化时,BP 网络模型会产生较大的误差。而 SAPO-BP 模型相对于传统的 BP 模型来说,它们的误差曲线幅度较为平缓,且变化幅度也稳定在了一定的范围之内。经过改进的 PSO-BP 网络模型,即加入自适应变异算子的 PSO-BP 网络模型相对于 BP 网络模型来说,其误差曲线幅度更加平缓,误差曲线的变化幅度也稳定在了更小的范围之内。从而说明 SAPSO-BP 网络模型有着更好的自适应和自纠错能力。为了更准确描述出网络模型的预测误差,使用均方根误差(RMSE)来进行比较。BP 以及 SAPSO-BP 网络模型预测结果的 RMSE 分别为 0.616 9°,0.375 2°。从而说明 SAPSO-BP 网络模型相对于 BP 模型有着更高的预测精度。
3.3 预测模型的对比分析为了进一步研究分析,使用另外几种不同的神经网络预测模型对“育鲲”轮的横摇运动进行实时预报仿真实验,仿真实验均使用相同的数据并在相同的仿真环境下进,所有模型均设置为 5 个输入节点和 1 个输出节点且仿真模型参数不变。这几种网络模型分别包括:RBF(Radical Basis Function)神经网络、WNN(Wavelet Neural Network)神经网络、传统 BP 神经网络、PSO-BP 神经网络以及 SAPSO-BP 神经网络。仿真实验的结果如表 2 所示。
|
|
表 2 仿真实验结果 Tab.2 Simulation results |
经过表 2 实验结果的对比可知,SAPSO-BP 网络预测模型的预测精度比另外几种模型的预测精度更高。而且 SAPSO-BP 预测模型的单步仿真时间比传统的其他模型更短一些。
4 结 语本文将 SAPSO-PB 算法应用于传统 BP 神经网络模型的网络参数优化中,克服了传统 BP 网络模型的对初始权值阈值敏感,容易陷入局部极小值的缺点,同时也克服了传统 PSO 算法的容易早熟收敛、搜索准确度低、迭代效率较低等缺点。提高了 PSO 算法的全局搜索能力,拓展了种群搜索的空间范围。并将 SAPAO-B 混合预测模型应用于船舶横摇运动的实时预报,仿真实验将该混合算法预测模型与传统的 BP 预测模型进行比较,验证了 SAPSO-BP 混合预测模型预测精度较高,收敛速度也相对较快,同时也具有良好的泛化性能。它为船舶横摇运动的实时预报提供了一种有效途径。但是本文仅仅使用 SAPSO-BP 模型进行了船舶横摇运动的较短期预报,因此使用该模型进行横摇运动的长期预报将是接下来的主要研究工作。
| [1] | FOSSEN T I. Handbook of marine craft hydrodynamics and motion control[M]. Hoboken N.J, USA:John Wiley & Sons Ltd., 2011:20-80. |
| [2] | FOSSEN T I. Guidance and control of ocean vehicles[M]. Chichester, New York, USA:John Wiley & Sons Ltd., 1994:10-100. |
| [3] | 郑丽颖. 混沌神经网络及模糊混沌神经网络的研究与应用[D]. 哈尔滨:哈尔滨工程大学, 2002. |
| [4] | 席剑辉. 混沌时间序列的长期预测方法研究[D]. 大连:大连理工大学, 2005. |
| [5] | LIN Y J. Prevention of transient instability employing rules based on back propagation based ANN for series compensation[J]. International Journal of Electrical Power & Energy Systems , 2011, 33 (10) :1776–1783. |
| [6] | BASERI H, BAKHSHI-JOOYBARI M, RAHMANI B. Modeling of spring-back in V-die bending process by using fuzzy learning back-propagation algorithm[J]. Expert Systems with Applications , 2011, 38 (7) :8894–8900. DOI:10.1016/j.eswa.2011.01.102 |
| [7] | 贾嵘, 薛建辉, 张文宇, 等. 基于邻域粒子群优化神经网络的异步电动机振动故障诊断[J]. 西安石油大学学报(自然科学版) , 2010, 25 (2) :73–75. |
| [8] | YIN J C, ZOU Z J, XU F, et al. Online ship roll motion prediction based on grey sequential extreme learning machine[J]. Journal of Neurocomputing , 2014, 129 :168–174. DOI:10.1016/j.neucom.2013.09.043 |
| [9] | KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of IEEE international conference on neural networks. Perth, WA, Australia:IEEE, 1995(4):1942-1948. |
| [10] |
刘永清, 孙江龙, 王嘉俊, 等. LNG船运动响应数值计算与试验研究[J]. 舰船科学技术 , 2016, 38 (3) :25–30.
LIU Yong-qing, SUN Jiang-long, WANG Jia-jun, et al. Numerical and experimental study of LNG ship motion response[J]. Ship Science and Technology , 2016, 38 (3) :25–30. |
| [11] |
刘胜, 邢博闻, 陈潇. 船舶信息系统数据流设计方案研究[J]. 舰船科学技术 , 2016, 38 (4) :110–115.
LIU Sheng, XING Bo-wen, CHEN Xiao. Design of data flow for ship information system[J]. Ship Science and Technology , 2016, 38 (4) :110–115. |
 2016, Vol. 38
2016, Vol. 38
