2. 船舶与海洋工程水动力湖北省重点实验室, 湖北 武汉 430074 ;
3. 高新船舶与深海开发装备协同创新中心, 上海 200240
2. Hubei Key Laboratory of Naval Architecture & Ocean Engineering Hydrodynamics, Wuhan 430074, China ;
3. Collaboration Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
随着全球气候变暖和 IMO 国际海事组织对于环保更严格的要求,节能减排已经成为船舶运营商不得不考虑的重要因素。纵倾调节在不改变船舶载重和航速的前提下,仅改变船舶航行过程中的纵倾角,进而减少其航行阻力,起到节能减排的功效。与其他节能减排方式相比,船舶纵倾调节具有易于实现、成本低廉、效果明显等优点。
Subramani 和 Paterson 等[1]在考虑船舶航态变化的前提下,对 FF1052 和 S60 采用 CFD 求解船舶阻力、姿态,将计算所得结果与实验值对比,整体变化趋势一致,幅值吻合良好。Yang 等[2]采用有限元法求解 Euler 方程,对比了自由模和拘束模的阻力,对 Wigley 和 S60 船的阻力和姿态采用非结构网格计算,结果与试验吻合良好。Gorski,Hino 等[3-4]使用了 RANS 方法计算船舶黏性流场,用于新型舰船的设计和分析,其中数值计算提供了各种球首变化的流场信息以及螺旋桨进流的流动信息,为设计提供了指导。高高等[5]用 Rankine 源面元法数值计算某内河大方形系数双尾船的浅水下沉量及纵倾,计算得出船体纵倾值随航速的变化趋势,并用试验验证计算结果。董文才等[6-7]提出滑行艇纵向运动的基本假设;建立计及浮性和滑行力、滑行力矩影响的滑行艇纵向运动基本方程,提出预报滑行艇纵向运动的实用计算方法(滑航法)并编制了理论预报程序。吴明等[8]同时求解 RANS 和刚体运动方程,计算 S60 躶船模在浅水中的流场,得出其下沉与纵倾值,并用试验验证,结果吻合。
然而,航行姿态对于肥大排水型船舶阻力的影响并没有太多研究。本文以 180 000 DWT 散货船为模型,使船舶处于不同倾角,通过 Fluent 选用k-ε 和k-ω 湍流模型计算得出不同倾角对应的阻力,并通过模型试验与计算值的对比,得出适合本船型的湍流模型。在这过程中,对比模型试验在不同纵倾角下阻力,探究纵倾调节对船舶阻力的影响,并得出船舶设计航速的最佳纵倾角。
1 控制方程采用 RANS 控制方程组,包括连续性方程和动量守恒方程,分别如下:
连续性方程:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial (\rho {u_i})}}{{\partial {x_i}}}{\rm{ = }}0\text{;} $ | (1) |
动量守恒方程:
| $ \begin{aligned} & \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}{u_j}} \right)}}{{\partial {x_j}}} =-\frac{{\partial \rho }}{{\partial {x_i}}} + \\ & \quad \quad \left. {\frac{\partial }{{\partial {x_i}}}\left[ {\mu (\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}})-} \right.\frac{2}{3}\mu \frac{{\partial {u_l}}}{{\partial {x_l}}}{\delta _{ij}}} \right] + \\ & \quad \quad \frac{\partial }{{\partial {x_j}}}\left( {-p\overline {{u_{i'}}{u_{j'}}} } \right) + \rho {f_i}\text{。} \end{aligned} $ | (2) |
式中:ui 为流体时均速度分量;p 为流体压强;fi 为流体体积力分量;ρ 为流体密度;μ 为流体的粘性系数;附加应力记为
| $ \begin{aligned} & \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho k{u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {{\alpha _k}{\mu _{eff}}\frac{{\partial k}}{{\partial {x_j}}}} \right] + \\ & \quad \quad \,\, \quad {G_k} + {G_b}-\rho \varepsilon \text{,} \end{aligned} $ | (3) |
| $ \begin{aligned} & \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho k{u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {{\alpha _k}{\mu _{eff}}\frac{{\partial k}}{{\partial {x_j}}}} \right] + \\ & \quad \quad \,\, {C_{1\varepsilon }}\frac{\varepsilon }{k}({G_k} + {C_{3\varepsilon }}{G_b}){G_k}-{C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k}-{R_\varepsilon }\text{。} \end{aligned} $ | (4) |
| $ \begin{aligned} {\text{式中:}}\ \ \ \quad\quad\quad\quad\quad\quad\quad& \varepsilon = \frac{\mu }{\rho }\left( {\frac{{\partial {\mu _i}}}{{\partial {x_k}}}} \right)\left( {\frac{{\partial {\mu _i}}} {{\partial {x_k}}}} \right)\text{,}\\ & {\mu _t} = \rho {C_\mu }\frac{{{k^2}}}{\varepsilon }\text{,}\\ & {\mu _{eff}} = \mu + {\mu _t}\text{。} \quad\quad\quad\quad \end{aligned} $ |
Gk 为平均速度梯度引起的湍流能k 的产生项;Gb 为浮力引起的湍动能k 的产生项;C1ε,C2ε,C3ε 为经验常数。
| $ \begin{aligned} & {G_k} = {\mu _t}\left( {\frac{{\partial {\mu _i}}}{{\partial {x_j}}} + \frac{{\partial {\mu _j}}}{{\partial {x_i}}}} \right)\frac{{\partial {\mu _i}}}{{\partial {x_j}}}\text{,}\\ & {G_b} = \beta {g_i}\frac{{{\mu _t}}}{{P{r_t}}}\frac{{\partial T}}{{\partial {x_i}}}\text{。} \end{aligned} $ |
在k-ε 模型中,根据 Launder 等的推荐值及后来的实验验证值,模型常数C1ε = 1.45,C2ε = 1.92,Cμ = 0.09。
2 数值计算计算模型按照缩尺比 λ = 1:55 换算,换算后主尺度如表 1 所示。
|
|
表 1 船舶主尺度 Tab.1 Principal parameter of ship modle |
计算模型在 UG NX 中完成。整个数值模拟区域约为 4 倍船长,空气和水的入口在船首上游L(1 倍船长)处,出口在尾部下游 2L 处,计算域侧面在距离船表面L 以外,底部在距离船底表面L/2 处。计算域模型如图 1 所示。

|
图 1 模型计算域 Fig. 1 The model of computational domain |
计算域的离散通过 ICEM 网格划分工具来完成,全部采用六面体网格,全局采用 H 型网格,船体附近采用 C 型网格。船体表面曲线变化较大,需要将船体分成多个 block 来进行网格划分,船体中间部分线型比较平缓,分成几个大的 block 形成质量高的六面体网格;而首尾曲线变化较大,需要分成多个小的 block 来形成六面体网格,这样不会出现扭曲率太大的网格。网格划分如图 2 所示。

|
图 2 船体表面网格 Fig. 2 Grid of ship surface |
自由面需要捕捉波形,靠近自由面附近网格较密,流场底部网格较稀。物面附近参数变化梯度大,网格太稀则误差较大;离物体很远处参数变化小,网格太密则浪费计算时间。在船体中部曲线较平缓,结构网格均匀分布;船体首尾曲线变化大,网格应该较密。网格线尽量正交,曲线光滑,尽量与流动方向一致。在所有的网格中,不能出现负体积,网格质量要满足计算要求。

|
图 3 船舶模型首尾部网格 Fig. 3 The grid of bow and stern |
计算过程中边界条件的设置如下:空气入口为速度入口,湍流强度为 0.1%,湍动粘度比为 1;水的入口为速度入口,湍流强度为 1%,湍动粘度比为 1。为了避免出口处回流的产生,给定其与入口相同的边界条件,计算区域的上面和空气入口条件相同,底面与侧面设定为壁面边界条件,船体表面为壁面边界条件,中间给定对称面条件,水流速度、密度、粘度与模型试验条件相同。
自由表面的求解选用了欧拉隐式 VOF 方法,它可用于定常和非定常计算。由于所关心的问题是最终的自由面情况,因此对于船的自由液面计算可以使用定常欧拉隐式 VOF 方法。为了能够较好的收敛,刚开始时间步长取为 0.001 s,当快要收敛的时候,时间步长取为 0.005 s,每个时间步长内迭代 20 次,对于不同的网格,不同的湍流模型,经过大概 100 s 左右的迭代后可以得到稳定的残差收敛曲线(见图 4)和阻力收敛曲线(见图 5)。
|
图 4 残差收敛曲线 Fig. 4 The residual convergence curve |
|
图 5 阻力收敛曲线 Fig. 5 The convergence curves of resistance |
压力的插值方法采用 PRESTO(Pressure Staggering Option),其他项都用 2 阶迎风格式进行离散,包括体积分数,选择求解自由面相对准确的几何重构等方法。速度压力的耦合方法为 SIMPLE(Semi-Implicit Method for Pressure-Linked Equations)方法。为了加快算法的收敛性,Fluent 软件采用了多重网格技术来加速收敛,即对网格进行粗细划分,先消除高频脉动的误差,再消除低频脉动的误差,直到收敛。
2.4 基于 RNGk-ε 湍流模型各倾角下阻力计算结果对计算结果重点需要观察船舶改变纵倾状态前后阻力值的变化,因此用纵倾阻力增减比能更好反映结果,如下:
| $\begin{aligned} & \text{纵倾阻力}\\ & \text{增减比}{\rm{ = }}\frac{{\text{改变纵倾后阻力}{\rm{-}}\text{平浮阻力}}}{\text{平浮阻力}} \times 100{\rm{\% }}\text{。} \end{aligned}$ |
表 2 为设计吃水D = 16.5 m 状态下,在航速为Vs = 15 kn 时,不同纵倾状态下选用 RNGk-ε湍流模型在 Fluent 中计算的阻力结果。
|
|
表 2 RNGk-ε 湍流模型不同倾角下 CFD 计算结果 Tab.2 The CFD calculation results of different trim underk-ε |
通过阻力增减百分比可看出,在设计吃水D = 16.5 m 的 5 个纵倾状态下,首倾角为 0.301 6° 时,阻力性能最优,相对平浮状态阻力减小 4.67%;其次是首倾角为 0.603 1° 时,相对平浮状态阻力减小 3.97%;而尾倾角为 0.603 1° 时,阻力性能最差,相对平浮状态阻力增大 2.93%;尾倾角为 0.301 6° 时,其阻力相对平浮状态阻力相差比较小。
2.5 基于 SSTk-ω 湍流模型各倾角下阻力计算结果表 3 为设计吃水D = 16.5 m 状态下,在航速为Vs = 15 kn 时,不同纵倾状态下选用 SSTk-ω湍流模型在 Fluent 中计算的阻力结果:
|
|
表 3 SSTk-ω 湍流模型不同倾角下 CFD 计算结果 Tab.3 The CFD calculation results of different trim underk-ω |
通过纵倾百分比曲线可看出,在设计吃水D = 16.5 m 的 5 个纵倾状态下,首倾角为 0.603 1° 时,阻力性能最优,相对平浮状态阻力减小 3.63%;其次是首倾角为 0.301 6° 时,相对平浮状态阻力减小 2.92%;而尾倾角为 0.603 1° 时,阻力性能最差,相对平浮状态阻力增大 2.49%;尾倾角为 0.301 6° 时,其阻力相对平浮状态阻力增大 0.63%。
2.6 各倾角下船体表面动压力分布图 6 ~图 10 展示的是设计吃水为D = 16.5 m,设计航速为Vs = 15 kn 时,在各倾角状态下,船体表面的动压力分布云图。

|
图 6 首倾为 0.603 1° 船体表面动压力分布云图 Fig. 6 Hydrodynamic pressure distribution under 0.603 1° trim angle |

|
图 7 首倾为 0.301 6° 船体表面动压力分布云图 Fig. 7 Hydrodynamic pressure distribution under 0.301 6° trim angle |

|
图 8 平浮船体表面动压力分布云图 Fig. 8 Hydrodynamic pressure distribution under 0° trim angle |

|
图 9 尾倾为 0.603 1° 船体表面动压力分布云图 Fig. 9 Hydrodynamic pressure distribution under-0.3016° trim angle |

|
图 10 尾倾为 0.603 1° 船体表面动压力分布云图 Fig. 10 Hydrodynamic pressure distribution under-0.6031° trim angle |
从上述云图可看出,D = 16.5 m,Vs = 15 kn 时,首倾状态下船体表面的动压力分布要明显优于尾倾状态下的船体表面压力分布。
3 模型试验模型试验按照缩尺比 λ = 1:55 制作船模,主尺度见表 1,试验拖曳形式为模型内拖,模型拖点高度在首尾平均吃水线上。模型如图 11 所示。

|
图 11 船舶模型 Fig. 11 Ship modle |

|
图 12 船模试验过程 Fig. 12 Ship modle test |
模型试验所得数据如表 4 所示。
|
|
表 4 模型试验测量结果 Tab.4 The modle test result |
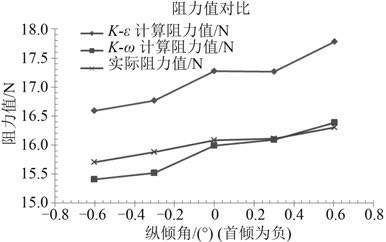
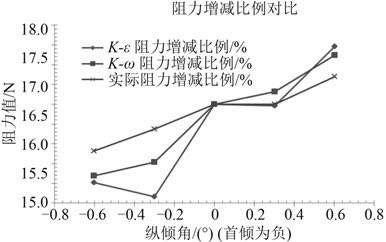
将模型试验所得出的数据与 CFD 计算得出的结果汇总并对比,得出该船舶在不同倾角过程中阻力对比曲线,如表 4所示。
|
图 13 不同倾角阻力值对比 Fig. 13 Resistance comparison of different trim angl |
|
图 14 不同倾角阻力值增减比 Fig. 14 Resistance increase or decrease ration comparison of different trim angl |
通过对比,可以看出计算结果与实验结果基本吻合,其增减趋势相同,且使用k-ω 湍流模型计算结果精度更高。
4 结 语本文以 180 000 DWT 散货船设计状态为基础,在 Fluent 中用k-ε 和k-ω 两种湍流模型分别求解不同倾角下阻力,并通过船舶模型试验验证,得出如下结论:
1)针对本散货船在不改变船舶航速、载重量的前提下,通过纵倾调节可以减少船舶阻力,达到节能减排的作用。
2)针对本散货船设计吃水、设计航速而言,使船舶首倾可以减少船舶行驶的阻力。首倾角在 0.301 6° 时可以减少 1.25% 的阻力,首倾角在 0.603 1° 时可以减少 2.36% 阻力。由此可看出,在设计载重设计航速下,对于节能减阻而言平浮不是最优航态,使船舶首倾能够提高阻力性能。
3)通过k-ε 和k-ω 两种湍流模型的结果与模型试验结果的对比,可以得出对于本肥大型散货船而言,选取k-ω 湍流模型计算更加合理的结论。
| [1] | SUBRAMANI A K, PATERSON E G, STERN F. CFD calculation of sinkage and trim[J]. Journal of Ship Research , 2000, 44 (1) :59–82. |
| [2] | YANG C, LÖHNER R. Calculation of ship sinkage and trim using a finite element method and unstructured grids[J]. International Journal of Computational Fluid Dynamics , 2002, 16 (3) :217–227. DOI:10.1080/10618560290034690 |
| [3] | GORSKI J J, HAUSSLING H J, PERCIVAL A S, et al. The use of a RANS code in the design and analysis of a naval combatant[C]//Proceedings of the 24th ONR Symposium on Naval Hydrodynamics. Fukuoka, Japan, 2002. |
| [4] | HINO T. Shape optimization of practical ship hull forms using navier-stokes analysis[C]//Proceedings of the 7th International Conference on Numerical Ship Hydrodynamics. Nantes, France:Ecole Centrale de Nantes, 1999. |
| [5] |
高高, 邹璐. 大方形系数双尾船浅水下沉量与纵倾计算[J]. 船海工程 , 2007, 36 (6) :15–17.
GAO Gao, ZOU Lu. Numerical calculation of sinkage and trim for high-block ships with twin-skeg navigating in shallow water[J]. Ship & Ocean Engineering , 2007, 36 (6) :15–17. |
| [6] |
董文才, 刘志华, 吴晓光, 等. 滑行艇波浪中纵向运动理论预报的新方法[J]. 船舶力学 , 2007, 11 (1) :55–61.
DONG Wen-cai, LIU Zhi-hua, WU Xiao-guang, et al. A new theoretical method on longitudinal motion of planing craft in wave[J]. Journal of Ship Mechanics , 2007, 11 (1) :55–61. |
| [7] |
董文才, 岳国强. 深V型滑行艇纵向运动试验研究[J]. 船舶工程 , 2004, 26 (2) :14–16.
DONG Wen-cai, YUE Guo-qiang. Experimental study on longitudinal motion of deep-V-shaped planning craft[J]. Ship Engineering , 2004, 26 (2) :14–16. |
| [8] | 吴明, 王骁, 杨波, 等. 舰船任意吃水——纵倾组合浮态阻力计算的CFD方法[C]//中国航海学会海洋船舶驾驶专业委员会2009年度学术研讨会论文集. 大连:中国航海学会, 2009. |
| [9] | 王福军. 计算流体动力学分析:CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004 : 124 . |
| [10] | 邵世明, 赵连恩, 朱念昌. 船舶阻力[M]. 北京: 国防工业出版社, 1995 . |
 2016, Vol. 38
2016, Vol. 38
