船体总振动固有频率是描述船体结构性能的一个重要参数,不良的振动会造成船体结构的严重损坏,影响舰船的经济性与战斗能力[1-2]。国军标规定[3]:第 1 阶总振动固有频率必须与主要激励的频率错开 8%~10%,第 2 阶总振动固有频率与主要激励的频率错开为 10%~12%。
舰船设计与建造是一个较长期的、庞大的、耗资巨大的工程,舰船设计一般分为方案设计、初步设计、技术设计和施工设计 4 个阶段。为保证舰船设计与建造的成功,在方案设计阶段就必须有正在设计舰船的船体总振动固有频率数据,使之与外界干扰力的频率错开一定范围[4]。
国军标规定了适用于舰船各个设计阶段的船体总振动固有频率近似计算方法[5],这些近似计算方法是基于船体梁弯曲振动基本振动特性和已有船的固有频率的统计规律而得出[6],经验公式中的统计系数来源于国外的舰船数据,所以这些公式估算出的固有频率值往往与实际的舰船总振动固有频率值差异较大。为解决这种情况,在编制大型舰船的总振动设计规范时,有关方面采用我国舰船的实际数据,对国外资料中的经验公式进行修正,进一步提高了大型舰船总振动固有频率近算方法的精确程度。
目前对于船体总振动低阶固有频率的估算,采用一维梁模型并计入附连水质量,是比较成熟的方法[7],并且在工程应用上能够获得足够准确的结果。本文以某舰船为母船,根据我国舰船设计规律设计出 177~200 m 船长范围的、利用船体等值梁法振动分析输入数据,并建立一维船体梁模型进行仿真计算,与现有船体二节点振动固有频率经验公式计算结果进行比较,分析了现有经验公式的差异,并提出修正系数,进一步完善固有频率的经验公式供设计师参考。
1 船体固有频率数学模型及近似计算公式大型舰船是庞大的水上建筑物。宏观上,主船体结构具有“瘦”、“长”的几何特点,对其进行总振动和总强度分析时,一般是将其抽象成一根“船体等值梁”的力学模型。抽象而成的“船体等值梁”是 1 根漂浮在水面的全自由梁,船体总振动,即是这根等值梁的弯曲振动。对于长度为l、截面积为A、弯曲刚度为EI、密度为ρ 的全自由弯曲振动梁,其 2 节点振动固有频率为[6]:
| $ f = {\left( {\frac{{4.730}}{{2\pi }}} \right)^2}\sqrt {\frac{{EI}}{{\rho A{l^4}}}} \text{,}$ | (1) |
如令
| $ \left. \begin{array}{l} \Delta = {C_1}\rho Al\\ B{H^3} = {C_2}EI\\ {L_{pp}} = l \end{array} \right\} \text{,}$ | (2) |
式中:∆ 为舰船排水量;B 为舰船型宽;H 为舰船型深;Lpp 为船长;
| $ \left. \begin{aligned} & {f_{v2}} = {C_3}\sqrt {\frac{B}{\Delta }} \sqrt {\frac{{{H^3}}}{{L_{pp}^3}}} \\ & {f_{h2}} = {C_4}\sqrt {\frac{B}{\Delta }} \sqrt {\frac{{{H^3}}}{{L_{pp}^3}}} \end{aligned} \right\} \text{,}$ | (3) |
式中
| $ \left. \begin{aligned} & {f_{v2}} = 0.94 \times {10^3}\sqrt {\frac{B}{\Delta }} \sqrt {\frac{{{H^3}}}{{L_{pp}^3}}} \\ & {f_{h2}} = 1.74 \times {10^3}\sqrt {\frac{B}{\Delta }} \sqrt {\frac{{{H^3}}}{{L_{pp}^3}}} \end{aligned} \right\}{\text{,}} $ | (4) |
式中fv2 和fh2 为船体垂向、水平向 2 节点振动固有频率,Hz。
在深化方案设计阶段,由于船体的中剖面惯性矩、浸水船宽、吃水深度为已知,故应利用这些数据,此时给出的大型舰船 2 节点总振动固有频率近似公式为:
| $ \left. \begin{aligned} & {f_{v2}} = \frac{{3.45}}{{\sqrt {1.2 + \frac{{{B_w}}}{{3D}}} }} \times \sqrt {\frac{{EI_{mid}^V}}{{L_{pp}^3}}} \\ & {f_{h2}} = \frac{{2.65}}{{\sqrt {1.2 + \frac{{{B_w}}}{{3D}}} }} \times \sqrt {\frac{{EI_{mid}^H}}{{L_{pp}^3}}} \end{aligned} \right\} \text{,}$ | (5) |
式中:
新准则在此基础上,进一步提出了大型舰船总振动固有频率近似计算公式。方案设计阶段计算船体 2 节点总振动固有频率的近似计算公式为:
| $ \left. \begin{aligned} & {f_{v2}} = {\rm{1}}.{\rm{03}}4 \times {10^3}\sqrt {\displaystyle\frac{B}{\Delta }} \sqrt {\frac{{{H^3}}}{{L_{pp}^3}}} \\ & {f_{h2}} = 1.{\rm{91}}4 \times {10^3}\sqrt {\displaystyle\frac{B}{\Delta }} \sqrt {\frac{{{H^3}}}{{L_{pp}^3}}} \end{aligned} \right\} \text{,}$ | (6) |
深化方案设计阶段船体 2 节点总振动固有频率近似公式为:
| $ \left. \begin{aligned} & {f_{v2}} = \displaystyle\frac{{3.{\rm{968}}}}{{\sqrt {1.2 + \frac{{{B_w}}}{{3D}}} }} \times \sqrt {\frac{{EI_{mid}^V}}{{L_{pp}^3}}} \\ & {f_{h2}} = \displaystyle\frac{{{\rm{3}}.{\rm{44}}5}}{{\sqrt {1.2 + \frac{{{D_w}}}{{3B}}} }} \times \sqrt {\frac{{EI_{mid}^H}}{{L_{pp}^3}}} \end{aligned} \right\} \text{。}$ | (7) |
为提高近似方法的准确性,最好的方法是依据实船数据得出式(3)的统计系数。式(6)和式(7)中的统计系数,是依据我国当时现有舰船数据而得出,而当时我国舰船的排水量均小于 8 000 t,其统计数据难以准确地反映大型舰船固有频率的变化规律。在该类型大型舰船的设计方面,我国的设计实践并不多,没有其他更多可用资料,该船的数据是建立大型舰船近似公式的重要基础。以现有某型舰船为母型船,根据我国舰船设计规律虚拟设计出 177~200 m 长的船体数据,用这些数据进行精确的总振动固有频率计算,用精确计算的结果得出式(3)的统计数据,从而得到适合我国大型舰船初步设计阶段的固有频率计算近似公式。
以母型船长度为起点,在 160~200 m 范围内按规律设定模拟船体的系列长度,设计扩展型的船长分别为 177 m(船型 1),189 m(船型 2),200 m(船型 3)。基于与母型船相同主尺度比(L/B,B/T,D/T 等)与方型系数,分别确定扩展型的船宽、吃水、型深与排水量,表 1 所示的主尺度符合我国舰船设计规律及主尺度之间的统计关系[8-9]。
|
|
表 1 虚拟船型船体主尺度参数 Tab.1 The virtual hull principal dimension parameters |
为了使固有频率的精确算法能在虚拟船型上使用,按母型船的剖面半宽、各段重量、剖面浸水、剖面型深、水下半横剖面积分布规律确定出各虚拟船型 21 个站位的上述剖面参数;利用各站剖面参数,按式(8)求出虚拟船的附连水质量分布和总附连水质量,其中浸没剖面面积系数β 根据母型船取值,表 2 和表 3 给出了各虚拟船 1~5 阶的垂向与水平向附连水质量。
| $ \begin{aligned} {m_v}(x) = \frac{\pi }{2}{\alpha _v}{k_i}{C_v}\rho {b^2}\text{,}\\ {m_h}(x) = \frac{2}{\pi }{\alpha _h}{k_i}{C_h}\rho {d^2}\text{。} \end{aligned} $ | (8) |
|
|
表 2 虚拟船型船体垂向总振动附连水质量 Tab.2 The added water mass of vertical vibration of the virtual hull |
|
|
表 3 虚拟船型船体水平总振动附连水质量 Tab.3 The added water mass of horizontal vibration of the virtual hull |
当所选择的母型船的船型与新设计的船型相同、结构形式和装载工况相似、且船长相差不超过 10% 时,在新设计船与母型船之间存在式(9)所示的关系[10]。
| $ \frac{{{N_{\rm{n}}}}}{{\sqrt {\frac{{{I_{\rm{n}}}}}{{{\Delta _{\rm{n}}}L_{\rm{n}}^3}}} }}({\text{新设计船}}){\rm{ = }}\frac{{{N_0}}}{{\sqrt {\frac{{{I_0}}}{{{\Delta _0}L_0^3}}} }}(\text{母型船}) \text{。}$ | (9) |
式中:Nn,In,∆n,Ln 分别为新设计船的总振动频率、中剖面惯性矩、总振动质量及设计水线长;N0,I0,∆0,L0 分别为母型船的总振动频率、中剖面惯性矩及总振动质量及设计水线长。
利用表 1 的数据,使用式(6)为各虚拟船设定一个总振动的首阶固有频率值。再利用表 2 和表 3 的数据,分别以表 1 船长序列中的、位于前面的船为母型,按式(9)求出紧邻的后面的1条虚拟船的中剖面惯性矩,如表 4 所示。
|
|
表 4 虚拟船型船体船舯剖面处惯性矩 Tab.4 The moment of intertia of the virtual hull midship section |
按母型船的剖面弯曲惯性矩分布规律确定各虚拟舰船船体各站剖面弯曲惯性矩,这样即获得了在技术设计阶段才能获得的、进行总振动固有频率精确计算所需的全部数据输入。国军标规定:总振动固有频率的精确计算采用船体等值梁力学模型,必须考虑舷外附连水质量。此方法所建立的大型舰船虚拟船体数据符合我国大型舰船的设计规律,且和实际设计计算用模型在所用参数、计算方法上均一致,可以保证研究结论的可靠、可用。
3 大型舰船船体总振动频率近似计算方法 3.1 船体梁模型仿真分析采用一维梁模型[6,11],即等效船体梁。船体总振动是在主船体结构层面上观察的一种振动,单体结构型式舰艇的主船体结构,其船长与宽度的比值、船长与型深的比值均比较大,特点是“细”、“长”,于是宏观上可把主船体结构视为“梁”,因而常以梁理论为基础建立舰艇总振动计算分析模型,即“船体梁”。等效船体梁是 1 根变截面梁,梁模型的惯性特性和刚度特性与实船结构等效,长度和边界条件与实船相等:1)船长与质量依据舰船的设计图纸和资料获得;2)采用附加质量法,将附连水质量的计算结果与干模态质量叠加;3)每一梁段的剖面惯性矩取为该梁段两端剖面惯性矩的平均值。因此由等效船体梁计算出的低阶振动特性即为实船的低阶振动特性;图 1 和图2 分别为虚拟船型 1(177 m)船体梁第 1 阶总振动示意图。
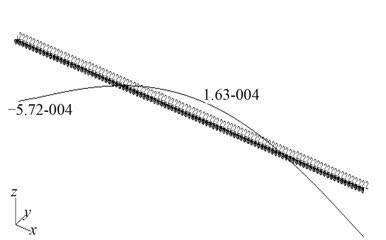
|
图 1 第 1 阶垂向总振动 Fig. 1 The hull vertical vibration |
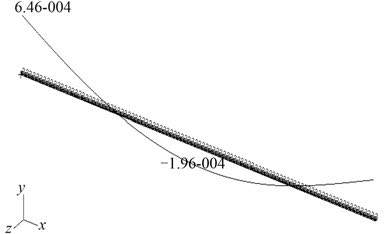
|
图 2 第 2 阶水平总振动 Fig. 2 The hull horizontal vibration |
利用式(6)和式(7)对船体 2 阶段的 2 节点振动固有频率进行估算。估算时用水线长代替垂线间长,用型宽代替浸水船宽。以下为母型船与虚拟船船体梁 2 节点总振动固有频率仿真计算结果与经验公式计算结果对比分析。船体梁计算结果与经验公式计算结果如表 5 和表 6 所示,图 3 和图 4 是船体梁计算结果与经验公式计算结果对比。
|
|
表 5 各船体垂向总振动固有频率 Tab.5 The hull vertical vibration natural frequency |
|
|
表 6 各船体水平总振动固有频率 Tab.6 The hull horizontal vibration natural frequency |
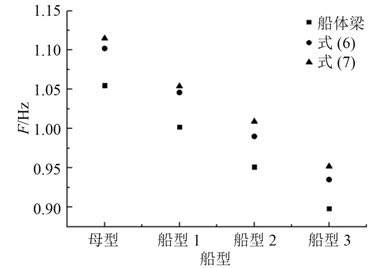
|
图 3 各船体垂向总振动固有频率 Fig. 3 The hull vertical vibrationnatural frequency |
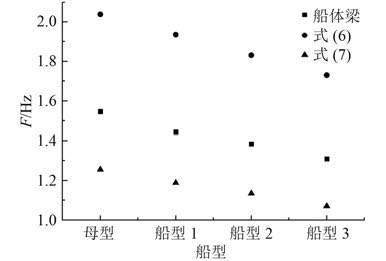
|
图 4 各船体水平向总振动固有频率 Fig. 4 The hull vertical vibration natural frequency |
分析以上数据可以得到:
1)随着船长的增大,其固有频率值逐步变小;
2)按母型船设计规律设计出的 177~200 m 船长范围内大型舰船的垂直向总振动固有频率计算值,与新准则中所推荐的设计阶段固有频率经验公式的垂直向总振动计算值符合良好,相互误差在 6% 左右;而水平向总振动计算值相互误差较大,达到 18%~30%;
3)虽然实船水平向总振动固有计算值与新准则中所推荐的设计阶段固有频率经验公式中水平向总振动计算值相互误差较大,但 2 种公式的估算结果误差波动幅值仅有
式(6)和式(7)主要是依据现有舰船(船长小于 160 m、排水量小于 8 000 t)数据资料对式(4)和式(5)进行修正而得出,在母型船实践的结果证明:其垂直向振动频率的估算较为准确、水平向固有频率值的估算误差较大,这由统计样本数据的局限性所造成,本文将统计样本数据扩展到 177~200 m 的范围,可以克服上述局限,提高近似公式的精度。依据本文的样本扩展数据,对式(6)和式(7)中的水平向固有频率近似公式提出进一步的修正系数η,即
| $ f_{h2}'{\rm{ = }}\eta {f_{h2}} \text{,}$ | (10) |
η 以本文的样本扩展数据为基础、按文献[12]的数据拟合方法而得出:
| $ \left\{ \begin{aligned} & {\eta _1} = 0.75\text{,}\text{方案设计阶段}\text{,}\\ & {\eta _2} = 1.2\text{,} \text{深化方案设计阶段}\text{。}\end{aligned} \right. $ | (11) |
修正后的两阶段水平向固有频率估算表达式分别为:
方案设计阶段
| $ \left. \begin{aligned} {f_{v2}} = {\rm{1}}.{\rm{03}}4 \times {10^3}\sqrt {\frac{B}{\Delta }} \sqrt {\frac{{{H^3}}}{{L_{pp}^3}}} \\ f_{h2}' = 1.436 \times {10^3}\sqrt {\frac{B}{\Delta }} \sqrt {\frac{{{H^3}}}{{L_{pp}^3}}} \end{aligned} \right\} \text{;}$ | (12) |
深化方案设计阶段
| $ \left. \begin{aligned} & {f_{v2}} = \frac{{3.{\rm{968}}}}{{\sqrt {1.2 + \frac{{{B_w}}}{{3D}}} }} \times \sqrt {\frac{{EI_{mid}^V}}{{L_{pp}^3}}} \\ & f_{h2}' = \frac{{4.134}}{{\sqrt {1.2 + \frac{{{D_w}}}{{3B}}} }} \times \sqrt {\frac{{EI_{mid}^H}}{{L_{pp}^3}}} \end{aligned} \right\} \text{。}$ | (13) |
通过以上研究,可以得出以下结论:
1)经验式(6)和式(7)基本符合固有频率变化规律,垂直向总振动固有频率估算值与精确方法计算结果具有较好的一致性,但水平向固有频率估算值与精确方法计算结果存在较大误差;
2)式(12)和式(13)可以提高方案设计阶段与深化方案设计阶段对舰船船体水平向总振动固有频率计算值的精度;
3)基于舰船设计规律设计出虚拟船型进行固有频率的精确计算可行,可将船长扩展到关注的任意船长范围。
| [1] |
王显正, 赵德有, 孙超, 等. 船舶总振动固有频率实用算法[J]. 中国舰船研究 , 2007, 2 (1) :56–58.
WANG Xian-zheng, ZHAO De-you, SUN Chao, et al. Improved algorithm for the natural frequencies of ship vibration[J]. Chinese Journal of Ship Research , 2007, 2 (1) :56–58. |
| [2] | 翁长俭, 张保玉. 船舶设计时振动的预防[J]. 武汉造船 , 1979 (1) :25–42. |
| [3] | 解放军总装备部军标出版发行部. 舰船通用规范:GJB 4000-2000[S]. 北京:总装备部军标出版发行部, 2000. |
| [4] |
陈翔, 夏利娟, 丁金鸿, 等. 散货船的总振动模态计算和动力响应预报[J]. 舰船科学技术 , 2013, 35 (3) :115–120.
CHEN Xiang, XIA Li-juan, DING Jin-hong, et al. The global vibration and dynamic response evaluation of a bulk carrier[J]. Ship Science and Technology , 2013, 35 (3) :115–120. |
| [5] | 水面舰艇结构设计计算方法:GJB/Z 119-99[S]. 北京:总装部军标出版发行部, 1999. |
| [6] | 陈志坚. 舰艇振动学[M]. 北京: 国防工业出版社, 2010 : 225 -226. |
| [7] | JOHANNESSEN H, SKAAR K T. Guidelines for prevention of excessive ship vibration[J]. SNAME Transaction , 1980, 88 :319–356. |
| [8] | 唐志拔. 水面舰艇设计[M]. 北京: 国防工业出版社, 1993 : 88 -99. |
| [9] | 邵开文, 马运义. 舰船技术与设计概论[M]. 北京: 国防工业出版社, 2005 . |
| [10] |
王晓宇, 伍友军. 某型测量船的船体总振动固有频率预报方法分析[J]. 船舶 , 2008, 19 (4) :18–26.
WANG Xiao-yu, WU You-jun. Prediction methods for global vibration natural frequency of a survey ship[J]. Ship & Boat , 2008, 19 (4) :18–26. |
| [11] | 郭日修, 索志强. 我国船舶振动研究的回顾与展望(下)[J]. 振动与冲击 , 1989 (2) :66–69. |
| [12] | 程正兴. 数据拟合[M]. 西安: 西安交通大学出版社, 1986 : 1 -97. |
 2016, Vol. 38
2016, Vol. 38
