2. 海军装备部驻上海沪东中华造船(集团)有限公司军事代表室, 上海 200000
2. Naval Military Representative Office in Hudong-zhonghua Shipbuilding(group) Co., Ltd., Shanghai 200000, China
空泡(亦称空化)是一种由于液体局部压力低于汽化压力而产生的液体汽化现象,它包括气穴(或者是气泡)的形成和溃灭[1]。空泡一般产生于螺旋桨、水翼和舵上,造成较为严重的水动力损失、噪声、剥蚀和振动等结果[2-3]。因此,研究空泡现象对于水动力研究至关重要。
片空泡作为一种主要的空泡形式,对升力的损失有着重要影响。同时,片空泡周期性的脱落还导致了流动的不稳定性,片空泡的溃灭也造成了振动和噪声等现象[4]。尽管试验观测在空泡的研究中依然有着不可取代的作用,但随着计算能力的飞跃式进步,通过数值计算的方式研究空泡现象得到越来越多人的认可。数值计算能提供试验难以测量的流场细节,方便学者进行深入研究。无论是试验观测还是数值模拟,尺度效应都是不可避免的问题。对实尺度的初始空泡数进行预报时,一般会先测量计算出尺寸较小模型的初始空泡数,再利用尺度效应公式推导出实尺度的初始空泡数。试验中模型尺度的雷诺数远小于实尺度,在模型尺度与实尺度的尺度换算中,尺度效应的影响不可忽略。
本文以翼剖面为 NACA0009 翼型的扭曲水翼为研究对象,通过建立在 LES 湍流模型上的 Zwart et al 空泡模型计算一定空泡数下的流动状态,并与实验值进行对比。在此基础上,分别计算出不同尺寸和速度下的初始空泡数,分析速度和尺寸变化对片初始空泡数的影响,回归出相应的函数曲线,提出新的片空泡尺度效应公式。
1 数值方法 1.1 LES 湍流模型湍流流动中包含着各种尺度的湍流结构,大尺度涡主要指尺寸大于平均流动(注:剪切层厚度)的湍流结构。与大尺度涡相比,小尺度涡主要起着耗散湍流能量的作用。基于该基本现象,LES 使用直接数值求解的方法计算大尺度涡,建立模型求解小尺度涡。模型中分离大小尺度涡的分界尺度称为过滤尺度,用 ∆ 表示。它相较于普通的 RANS 模型要求更细致的网格分布和更多的计算资源[5]。
进行大涡模拟一般有以下 3 个步骤:首先将流动的物理量分解为可解尺度和不可解尺度,常用的方法为低通过滤;其次,要给出大尺度涡的控制方程;最后,还需要小尺度脉动对大尺度脉动的封闭模型。
LES 的控制方程为:
| $ \frac{{\partial \overline {{u_i}} }}{{\partial t}} + \frac{{\partial \overline {{u_i}{u_j}} }}{{{x_i}}} =-\frac{1}{\rho }\frac{{\partial \overline p }}{{\partial {x_i}}} + \nu \frac{{{\partial ^2}\overline {{u_i}} }}{{\partial {x_i}\partial {x_j}}} + \frac{{\partial \overline {{\tau _{ij}}} }}{{\partial {x_j}}}, $ | (1) |
其中
| $ \overline {{\tau _{ij}}} = {L_{ij}} + {C_{ij}} + {R_{ij}}, $ | (2) |
其中Lij,Cij 和Rij 分别为:
| $ {L_{ij}} = (\overline {{u_i}} \overline {{u_j}}-\overline {\overline {{u_i}} \overline {{u_j}} } ), $ | (3) |
| $ {C_{ij}} = (\overline {\overline {{u_i}} u_j^{''}}-\overline {\overline {{u_j}} u_i^{''}} ), $ | (4) |
| $ {R_{ij}} =-\overline {u_i^{''}u_j^{''}} {\text {。}} $ | (5) |
式中:Lij 为 Leonard 应力,表示大尺度涡之间的相互作用;Cij 为交互应力,表示大尺度涡和小尺度涡之间的相互作用;Rij 为亚网格雷诺应力,表示小尺度涡之间的相互作用。
1.2 Zwart et al 空泡模型通过假设系统内所有气泡具有相同的尺寸,Zwart 提出使用气泡密度(n)来计算整个单位体积内汽液相间质量传输率(R),单个气泡的质量传输率为:
| $ R = n \times \left( {4\pi R_B^2{\rho _v}\frac{{D{R_B}}}{{Dt}}} \right), $ | (6) |
代入n 的值,可以得到净质量传输的表达式:
| $ R = \frac{{3\alpha {\rho _v}}}{{{R_B}}}\sqrt {\frac{2}{3}\frac{{{P_B}-P}}{{{\rho _l}}}}, $ | (7) |
从式(1)可以得到,单位体积内的质量传输率仅仅与气相密度(ρv)有关,在该模型中,R 与液相以及混合密度无关。最终的空泡模型如下:
当P ≤Pv 时:
| $ {R_e} = {F_{vap}}\frac{{3{\alpha _{nuc}}(1-{\alpha _v}){\rho _v}}}{{{R_B}}}\sqrt {\frac{2}{3}\frac{{{P_B}-P}}{{{\rho _l}}}}\text{,} $ | (8) |
当P >Pv 时:
| $ {R_c} = {F_{cond}}\frac{{3{\alpha _v}{\alpha _v}{\rho _v}}}{{{R_B}}}\sqrt {\frac{2}{3}\frac{{{P_B}-P}}{{{\rho _l}}}} {\text {。}} $ | (9) |
式中:RB = 10-6 m 为气泡半径;αnuc = 5 × 10-4 为气核体积分数 ;Fvap = 50 为汽化系数;Fcond = 0.01 为凝结系数 。
2 计算模型和网格划分计算模型为矩形翼的扭曲水翼,弦长 0.15 m,展长 0.3 m,剖面为 NACA0009 翼型,其中,攻角α($\overline z$)为关于无因次距离 $\overline z$ 的三次多项式函数,具体表达式为:
| $ \alpha (\overline z ) = {\alpha _{\max }}\left( {2{{\left| {\overline z } \right|}^3}-3{{\overline z }^2} + 1} \right) + {\alpha _{wall}}{\text {。}} $ | (10) |
其中
|
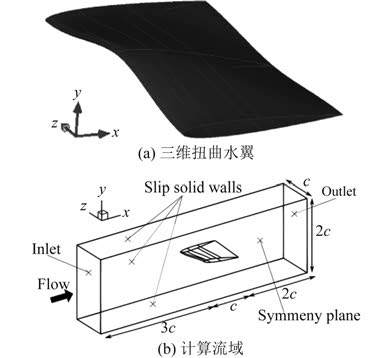
图 1 三维扭曲水翼和计算流域 Fig. 1 Geometry of 3D twisted hydrofoil and domain used in computations |
根据计算域的几何形状,主要使用 O-H 型网格对计算域进行整体网格划分,第 1 层网格尺度y+ 在 1-30 之间,网格数量为 700 万。图 2 所示为 LES 模型的网格划分。

|
图 2 计算网格图 Fig. 2 Overall view of computational domain grid |
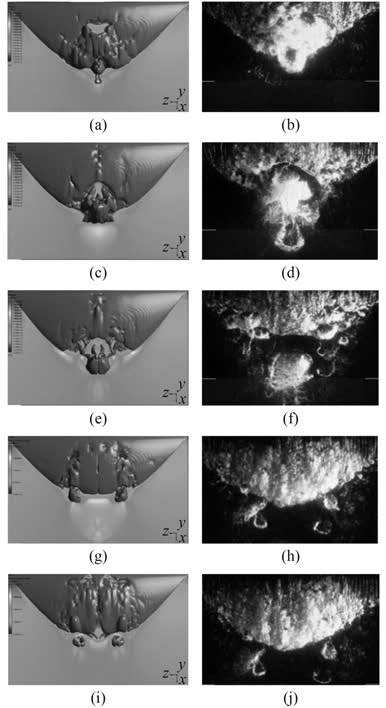
为与试验条件保持一致,设定空泡数为 1.07,出口处压力设置为 29 484 Pa,使用建立在 LES 湍流模型上的 Zwart et al 空泡模型计算水翼流场。图 3 给出了一个周期内片空泡生成和脱落的 CFD 计算结果和试验结果[6]。CFD 显示结果为αV = 0.1 的等值面。其中,αV 为蒸汽体积分数。
|
图 3 (a),(c),(e),(g),(i)为单周期内LES计算结果;(b),(d),(f),(h),(j)为试验结果 Fig. 3 (a), (c), (e), (g), (i) are LES results of one shedding cycle, (b), (d), (f), (h), (j) are videos of image |
如图 3 所示,LES 湍流模型的计算结果与实验结果吻合较好,不仅能模拟出空泡形成的准确区域,还清楚完整显示了片空泡的脱落过程,包括初次脱落、二次脱落及空泡雾化等具体细节。这显示了 LES 湍流模型在模拟空泡方面的显著优势。片空泡的脱落周期分以下几个步骤:
1)第 1 阶段(图 3(a)和图 3(b))。此时片空泡以达到最大尺寸,空泡边线处出现许多微小气泡(由于网格密度的问题,CFD 模拟中不能捕捉到该气泡),同时,在片空泡的尾端处已出现小范围空隙,该空隙在 LES 计算结果中也有清楚的显示。
2)第 2 阶段(图 3(c)~图 3(f))。此时由于回射流的影响,完整的片空泡被逐渐分割开来,尾端小块的空泡开始聚集起来并发生初次脱落。一般认为回射流位于气穴下方,在空泡体积未达到最大时便已出现,是导致空泡脱落的重要原因[7]。脱落的空泡因压力原因逐渐稀释变为雾状空泡并慢慢消失。
3)第 3 阶段(图 3(g)~图 3(j)。当初次脱落完成后,附着片空泡在尾端的左右两侧开始发生二次脱落,脱落过程与初次脱落相似,但脱落的空泡体积较小。在二次脱落完成以后,片空泡的体积开始逐渐增大,开始进入下一脱落周期。
4 片空泡尺度效应研究 4.1 速度影响研究一般研究认为,同一尺寸模型在保证空泡数不变的情况下改变来流速度,应该有相同的空泡形态:随着流速的改变,空泡发展的面积没有明显的变化[8]。表 1 给出了不同来流速度下水翼初始空泡数的大小。从中分析发现,不同来流速度下初始片空泡数σ 的变化幅度小于 2%,且初始片空泡数与来流速度的相关性较差。虽然来流速度的变化显著的影响着片空泡生成的临界压力值,但从总体上来说,空泡数保持在一个相对稳定的范围内,可以得出结论:来流速度对初始片空泡数基本无影响。这也进一步印证了经典空泡理论的相关结论(注:在这里认为总蒸汽体积分数Vvap 介于 1.2 × 10-8~1.4 × 10-8 时空泡处于初生状态)。Vvap 的表达式为:
|
|
表 1 不同流速下初始空泡数 Tab.1 The cavitation inception number at different velocity |
| $ {V_{vap}} = \sum\limits_{i = 1}^N {{\alpha _i}} {V_i}{\text {。}} $ | (11) |
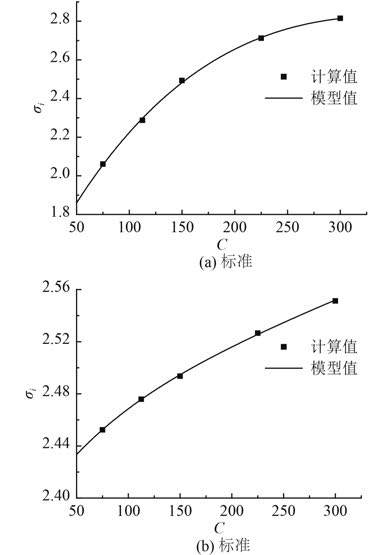
一般来讲,尺寸差异带来的影响是尺度效应研究的主要内容。与速度影响相同,随着尺度增大,空泡发展的绝对面积越大。因此,为保证水翼处于空泡初生状态,在增大尺寸的同时,必须同时提高环境压力,也就是增大初始空泡数。对于不同尺寸的空泡初生状态,可以从以下 2 个标准进行判断:一是设定总蒸汽体积分数Vvap 为一定值;二是设定Vvap 为随着尺度变化的变量。标准 1 只考虑了环境中水蒸汽含量,认为水蒸汽含量达到一定便判定空泡初始;标准 2 则认为在判定空泡初始时,各尺寸应具有相同的空泡发展情况。图 4 给出了不同尺寸在 2 个标准下下水翼初始空泡数的大小。
|
图 4 初始片空泡数尺度效应图 Fig. 4 Size scale effect of sheet cavitation inception number |
使用 Matlab 对离散点作曲线回归,得到相应的函数表达式,其中x 为三维水翼的弦长:
| $ {\sigma _i} = a \cdot {e^{bx}} + c \cdot {e^{dx}}{\text {。}} $ | (12) |
a,b,c,d 的具体值如表 2 所示。
|
|
表 2 函数变量值 Tab.2 The varible value of function |
图 4 显示了模型尺度对初始片空泡数的影响。从中分析发现,标准 1 下,初始片空泡数的变化幅度较大(介于 1.9~2.8 之间),且随尺度增大呈相关变化;而标准 2 下尺度变化对初始片空泡数有影响,但影响较小(介于 2.43~2.56 之间)。从以上分析可以得出结论,除对产生水蒸汽的含量有较高要求的领域外,尺寸的改变对片空泡的形成和发展有影响,但该影响并不大。图 5 显示了在相同空泡数,不同尺寸下三维水翼片空泡的计算结果。从中可发现,三维水翼空泡发展的相对面积有差别,但该差别很小,这也印证了标准 2 的计算结果:在片空泡具有相同发展面积的情况下,各尺寸模型的空泡数相差不大。从对图 5 的分析中也可进一步得出结论:不同尺寸下片空泡发展的相对面积相差不大,也可以说明片空泡的尺度效应影响较小。

|
图 5 片空泡尺度效应图 Fig. 5 Size scale effect of sheet cavitation |
在对初始片空泡数尺度效应公式的运用中,当涉及的具体工况对产生水蒸汽的含量有较高要求时,建议采用标准 1 的尺度效应公式;除此之外,建议使用标准 2 的尺度效应公式。
5 结 语本文应用 LES 模型计算了翼剖面为 NACA0009 翼型的扭曲水翼片空泡,并研究了来流速度和模型尺寸对片空泡初生和发展的影响,得到了以下结论:
1)LES 湍流模型的计算结果与实验结果吻合较好,不仅能模拟出空泡形成的准确区域,还清楚完整的显示了片空泡的脱落过程,包括初次脱落、二次脱落以及空泡雾化等具体细节。
2)虽然来流速度的变化显著的影响着片空泡生成的临界压力值,但从总体上来说,空泡数保持在一个相对稳定的范围内,可以得出结论:来流速度对初始片空泡数基本无影响。
3)除对产生水蒸汽的含量有较高要求的领域外,尺寸的改变对片空泡的形成和发展有影响,但该影响并不大。总的来说,片空泡的尺度效应影响较小。
| [1] | BRENNEN C E. Cavitation and bubble dynamics[M]. Cambridge: Cambridge University Press, 2013 . |
| [2] | GHORBANI M, ALCAN G, YILMAZ D, et al. Visualization and image processing of spray structure under the effect of cavitation phenomenon[J]. Journal of Physics:Conference Series , 2015, 656 (1) :012115. |
| [3] | WU J Y, WANG G Y, SHYY W. Time-dependent turbulent cavitating flow computations with interfacial transport and filter-based models[J]. International Journal for Numerical Methods in Fluids , 2005, 49 (7) :739–761. DOI:10.1002/(ISSN)1097-0363 |
| [4] | WU J Y, UTTURKAR Y, SENOCAK I, et al. Impact of turbulence and compressibility modeling on three-dimensional cavitating flow computations[C]//Proceedings of the 33rd AIAA fluid dynamics conference and exhibit. Orlando, Florida:AIAA, 2003. |
| [5] | DEHGHAN M, TABRIZI H B. Turbulence effects on the granular model of particle motion in a boundary layer flow[J]. The Canadian Journal of Chemical Engineering , 2014, 92 (1) :189–195. DOI:10.1002/cjce.v92.1 |
| [6] | FOETH E J, VAN TERWISGA T. The structure of unsteady cavitation. Part I:observations of an attached cavity on a three-dimensional hydrofoil[C]//Proceedings of the 6th international symposium on cavitation. Wageningen, The Netherlands:CAV, 2006. |
| [7] | DULAR M, KHLIFA I, FUZIER S, et al. Scale effect on unsteady cloud cavitation[J]. Experiments in Fluids , 2012, 53 (5) :1233–1250. DOI:10.1007/s00348-012-1356-7 |
| [8] | YANG Q F, WANG Y S, ZHANG Z H. Scale effects on propeller cavitating hydrodynamic and hydroacoustic performances with non-uniform inflow[J]. Chinese Journal of Mechanical Engineering , 2013, 26 (2) :414–426. DOI:10.3901/CJME.2013.02.414 |
 2016, Vol. 38
2016, Vol. 38
