众所周知,运动体在水中所受的阻力远远大于其在空气中所受的阻力,因此传统的水下武器的速度很难超过 35 m/s[1]。超空泡技术的出现克服了这一限制水下运动体发展的瓶颈。它的原理是:当水中航行体速度不断增大时,根据伯努利效应,其承受的水压力减小,当水压力减小到可以让常温的水变成水蒸气的程度时,水蒸气构成的气泡进而均匀地覆盖在航行体上,将航行体与水分开,水的阻力就变为由水蒸气构成的气泡的阻力,实现了航行体在水中飞行[2]。然而,在超空泡航行体高速运动的同时,由于航行体的尾部与空泡壁的接触会产生复杂的非线性滑行力,所以超空泡航行体系统为非线性动力学系统。
非线性系统的拓扑结构会随着系统参数的变化而发生定性变化,即出现分叉现象。因此,非线性系统中的一些失稳、颤振等现象就可能与系统产生分叉、混沌等动态有关,从而研究参变非线性系统中分叉的控制,以保证系统当参数在某一给定的范围内变化时仍工作在稳定状态,既有理论意义,又有应用价值[3-4]。Lin等[5]提出超空泡航行体系统随参数变化会产生分叉现象;白涛等[6]运用分叉法对超空泡航行体的运动稳定性进行了分析。本文运用非线性科学中的分叉理论系统地分析超空泡航行体的运动特性,通过分叉研究,揭示非线性的影响,并通过调整控制项来扩大系统稳定运动的参数范围。
本文基于 Dzielski 和 Kurdila[7]的超空泡航行体动力学模型,分叉分析系统随空化数变化产生的非线性动力学现象,基于分叉理论探讨不同空化数下航行体运动特性,并运用二维分岔图揭示空化数与控制律同时变化时对航行体稳定性的影响。
1 水下超空泡航行体的动力学模型 1.1 空化数的描述空泡在起始与发展过程中具有不同的形态,不同条件下发生的空泡也有不同的形状,按照空泡流型空泡可分为瞬态孤立空泡、附着空泡和空化涡[8]。为研究一般情况下的空泡形态,引用反映空泡的无量纲空化数,其表达式为:
| $ \sigma = \frac{{2\left( {{p_\infty }-{p_c}} \right)}}{{\rho {V^2}}}\text{。} $ | (1) |
式中:P∞ 为外压;Pc 为空泡内压;ρ 为水的密度;V 为航行体总速度[8]。
1.2 水下超空泡航行体动力学建模如图 1 所示,本文研究航行体在纵平面内的运动,当超空泡航行体在水下高速运动时,受到的力主要有空化器上的升力 Fcavitator、尾翼上的升力 Ffins、航行体质心位置的重力 Fgravity 及滑行力 Fplaning。

|
图 1 超空泡航行体示意图 Fig. 1 The schematic diagram of supercavitating vehicles |
超空泡航行体动力学建模的体坐标系原点位于航行体头部圆盘形空化器顶端面的圆心,把地面系当作惯性系,X 轴与航行体对称轴重合指向前,Z 轴垂直于 X 轴指向下。航行体 Z 轴方向的速度 w,方向与航行体轴线垂直;V 代表纵平面内航行体头部空化器的合速度,方向与航行体轴线平行;θ 是航行体俯仰角,q 是体坐标系下的俯仰角速度,z 是航行体的深度,建模采用 z,w,θ,q 作为 4 个状态变量来描述超空泡航行体的动力学。此外,该系统有 2 个控制输入,1 个是空化器偏转角 δc,另 1 个是尾翼偏转角 δe。上述变量有如下关系[5]:
| $ \begin{aligned} & \left( {\begin{array}{*{20}{l}} {\dot z}\\ {\dot w}\\ {\dot \theta }\\ {\dot q} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0&1&{-V}&0\\ 0&{{a_{22}}}&0&{{a_{24}}}\\ 0&0&0&1\\ 0&{{a_{42}}}&0&{{a_{44}}} \end{array}} \right)\left( {\begin{array}{*{20}{l}} z\\ w\\ \theta \\ q \end{array}} \right) + \\ & \quad \left( {\begin{array}{*{20}{l}} 0&0\\ {{b_{21}}}&{{b_{22}}}\\ 0&0\\ {{b_{41}}}&{{b_{42}}} \end{array}} \right)\left( {\begin{array}{*{20}{l}} {{\delta _e}}\\ {{\delta _c}} \end{array}} \right) + \left( {\begin{array}{*{20}{l}} 0\\ {{c_2}}\\ 0\\ 0 \end{array}} \right) + \left( {\begin{array}{*{20}{l}} 0\\ {{d_2}}\\ 0\\ {{d_4}} \end{array}} \right){F_{\rm planing}}\text{。} \end{aligned} $ | (2) |
式中 c2 为重力加速度。aij,bij,dij 的表达式如下[5]:
| $\begin{align} & {{a}_{22}}=\frac{CVT}{m}(\frac{-1-n}{L})S+\frac{17}{36}nL\text{,} \\ & {{a}_{24}}=VTS(C\frac{-n}{m}+\frac{7}{9})-VT(C\frac{-n}{m}+\frac{17}{36})\frac{17}{36}{{L}^{2}}\text{,} \\ & {{a}_{42}}=\frac{CVT}{m}(\frac{17}{36}-\frac{11n}{36})\text{,} \\ & {{a}_{44}}=\frac{-11CVTL}{36m}\text{,} \\ & {{b}_{21}}=\frac{C{{V}^{2}}Tn}{36m}(\frac{-S}{L}+\frac{17L}{36})\text{,} \\ & {{b}_{22}}=\frac{-C{{V}^{2}}TS}{mL}\text{,} \\ & {{b}_{41}}=\frac{-11C{{V}^{2}}Tn}{36m}\text{,} \\ & {{b}_{42}}=\frac{17C{{V}^{2}}T}{36m} \\ \end{align}$ |
| $ \begin{aligned} {c_2} = & g,{d_2} = \frac{T}{m}(\frac{{-17L}}{{36}} + \frac{S}{L}) \text{,}\\ {d_4} = & \frac{{11T}}{{36m}} \text{,}\\ S = & \frac{{11}}{{60}}{R^2} + \frac{{133}}{{405}}{L^2} \text{,}\\ T = &\frac{1}{{7S/9-289{L^2}/1296}} \text{,}\\ {C_x} = & {C_{x0}}(1 + \sigma ) \text{,}\\ C = & 0.5{C_x}\frac{{R{{_n^2}^{}}_{}}}{{{R^2}}} \text{,}\\ {R_c} = & {R_n}\sqrt {0.82\frac{{1 + \sigma }}{\sigma }} {K_2} \text{,}\\ {K_1} = &\frac{L}{{{R_n}(\frac{{1.92}}{\sigma }-3)}}-1 \text{,}\\ {K_2} = & \sqrt {1-(1-\frac{{4.5\sigma }}{{1 + \sigma }})} K_1^{40/17} \text{,}\\ {{\dot R}_c} = & {\frac{{\frac{{-20}}{{17}}(0.82\frac{{1 + \sigma }}{\sigma })}}{{{K_2}(\frac{{1.92}}{\sigma }-3)}}^{0.5}} \text{,}\\ V(1-& \frac{{4.5\sigma }}{{1 + \sigma }}){({K_1})^{23/17}}\text{。} \end{aligned} $ |
式中:L 为航行体长度;n 为尾翼效率,即航行体尾翼浸入水中的长度与总长度之比;m 为航行体对水的密度比;g 为重力加速度;Cx0 为空化器升力系数;Rn 为空化器半径;Rc 为空泡半径;R 为航行体半径;

|
图 2 浸没深度 Fig. 2 Immersion length |
模型考虑了复杂的非线性滑行力 Fplaning,该力由于航行体尾部与空泡壁接触时产生。其表达式为[5]:
| $ {F_{\rm planing}} =-{V^2}[1-{(\frac{{{R_c}-R}}{{h'R + {R_c}-R}})^2}](\frac{{1 + h'}}{{1 + 2h'}})\alpha \text{。} $ | (3) |
非线性滑行力的出现不仅会增加航行体的摩擦阻力,还会给航行体造成振动与冲击,产生分岔、混沌等复杂的非线性现象[4-5]。如何有效控制超空泡航行体的姿态,避免滑行力出现、减少航行体与空泡壁碰撞产生的冲击,是保证航行体在水下稳定运动的关键。
如图 3 所示,超空泡航行体尾部浸入水中的深度称为浸没深度,浸没深度 h′ 和航行体浸没角 α 的表达式为[5]:
| $ h' = \left\{ \begin{aligned} & 0,\;\;\left| w \right| < {w_{th}} = \frac{{\left( {{R_c}-R} \right)V}}{L}\text{,}\\ & \frac{{L\left| w \right|}}{{RV}}-\frac{{{R_C}-R}}{R},\;\;\;{\rm otherwise}\text{;} \end{aligned} \right. $ | (4) |
| $ \alpha = \left\{ \begin{aligned} & \frac{{w-{{\dot R}_c}}}{V},\;\;\;\frac{w}{V} > 0\text{,}\\ & \frac{{w-{{\dot R}_c}}}{V},\;\;\;\;{\rm otherwise}\text{;} \end{aligned} \right. $ | (5) |
在式(4)中,当 |w| > wth 时,浸没深度 h′ > 0;当 |w| < wth 时,浸没深度 h′ = 0,wth 为临界分界点。
2 水下超空泡航行体运动状态分析 2.1 分叉理论设超空泡航行体的动力学微分方程可以用如下非线性动力学系统的一般形式来描述,即
| $ {\dot x} = {f}({x},{\mu })\text{。} $ | (6) |
式中:x =(x1 x2 … xn)T∈Rn 为状态变量,对应于超空泡航行体动力学微分方程组中的深度、垂直速度、俯仰角和俯仰角速度(即 z,w,θ,q);μ=(μ1 μ2 … μm)T∈Rm 为控制变量,对应于超空泡航行体的空化数 σ、空化器偏转角 δc 和尾翼偏转角 δe;f=(f1 f2 … fn)T:Rn × Rm→Rn,对应于 z,w,θ,q 对时间 t 的变化率函数。
根据分岔理论,首先进行奇异性分析。奇异点由如下方程得到[9]:
| $ {f}({x},{\mu }) = 0\text{,} $ | (7) |
| $ det{{D}_x}{f}({x},{\mu }) = 0\text{。} $ | (8) |
式中 Dxf(x,μ)为 f(x,μ)对 x 的 Jacobi 矩阵,即 Dxf(x,μ)=(
| $ x(t) = A(\mu )x(t) + F(x(t),\mu )\text{。} $ | (9) |
式中:
1)若 A(μ)的特征根均存在负实部,可判定系统稳定;
2)若 A(μ)的特征根中有 1 对共轭纯虚特征根,而其他特征根均有负实部,可利用中心流形定理对系统进行降维约化后分析其稳定性;
3)若 A(μ)的特征根有 1 对纯虚特征根,则说明系统在此处发生 hopf 分叉,开始从平衡态失稳并产生周期振荡。
2.2 超空泡航行体分叉分析根据所建立的超空泡航行体系统的四维动力学方程(2),分析水下航行体动力学特性。超空泡航行体的系统参数值为:重力加速度 g = 9.81 m/s2,密度比 m = 2;尾翼效率 n = 0.5;空化器半径 Rn = 0.019 1 m;航行体半径 R = 0.050 8 m;航行体长度 L = 1.8 m;空化数的有效范围是 σ∈[0.019 8,0.036 8]。升力系数 Cx0 = 0.82。
超空泡航行体设有反馈控制器,Dzielski 和 Kurdila[7]提出了经典的反馈控制律,分别为 δe = 0 和 δc = 15z-30θ-0.3q。基于此控制律,系统状态变量 w 随空化数 σ 变化的分叉图如图 3 所示。
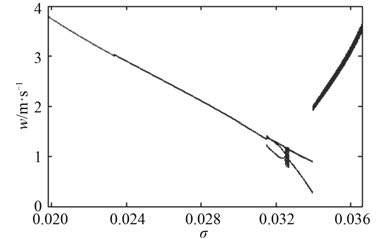
|
图 3 系统随空化数 σ 变化的分岔图 Fig. 3 Bifurcation diagram of system for σ |
如图 3 示,在经典反馈控制率的条件下,当系统处于小空化数 σ∈[0.019 8,0.024 2]时,图中左上细黑线段稳定平衡点说明航行体处于稳定运动的状态;σ = 0.242 5 时,系统发生 hopf 分岔,系统由稳定的有界点突变到极限环,空化数 σ∈[0.024 25,0.031 78] 时,极限环的出现将使航行体平衡态失稳并产生周期振荡[5];经过一系列倍周期分岔,空化数 σ∈[0.031 78,0.036 8] 时,系统进入混沌状态,航行体将剧烈振荡甚至倾覆。
2.3 不同空化数下航行体运动状态分析根据超空泡航行体分叉分析,在超空泡航行体稳定运动范围 [0.019 8,0.024 2] 内任取 σ = 0.021 0,以该点为代表分析航行体的运动状态。
令系统方程(2)的
在平衡点处求系统方程(2)的近似线性化形式,得到 Jacobi 矩阵为:
| $ { { J{ s}}_1}\!\!=\!\!\left[\! {\begin{array}{*{20}{c}} {239.92}\!\! & \!\!{495.62}\!\! & \!\!{40011.91}\!\! & \!\!{-20005.95}\!\!\\ \!\!{-276.88}\!\! & \!\!{-326.42}\!\! & \!\!{-3195.02}\! & \!\!{15975.10}\!\!\\ 0 & 1 & 0 & 0\\ 1 & 0 & \!\!{-89.64}\!\! & 0 \end{array}}\! \right]\text{,} $ |
根据其特征方程:
| $ \det \left( {1\lambda-{{J}_S}} \right) = 0\text{,} $ |
可解得特征根为 λ1,2 =-27.860 ± j327.339,λ3,4 =-15.761 ± j34.334。由分叉理论可知,系统在平衡点处所有特征根均存在负实部,故系统处于稳定状态。
取初始状态为 [0,0,0,0],σ = 0.021 0 时得到系统仿真结果如图 4 所示。由图 4(a)~图 4(d)可知:系统各个状态变量初始时刻的值较大,在反馈控制律的作用下系统的各个变量都逐渐吸引到稳定平衡点 S1 上。图 4(e)~图 4(f)显示尾部伸出空泡长度 h′ 以及滑行力 Fplaning 也都恒定在确定值上。不难看出,航行体在小空化数下高速航行时,尾部一直处于穿过空泡浸入水中的状态,此时由头部的空化器和尾翼升力以及尾部的滑行力共同维持航行体的平衡,航行体处于稳定航行状态,由此也验证了上节分叉理论对系统稳定性的判定。
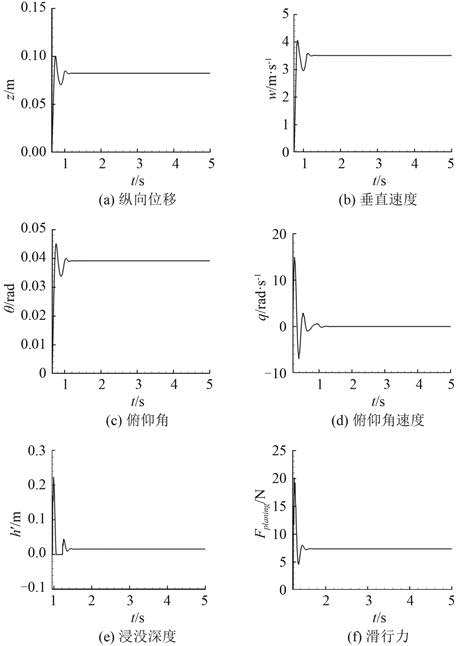
|
图 4 σ = 0.021 0 时系统响应示意图 Fig. 4 Time response for σ = 0.021 0 |
由分叉分析可知,当空化数 σ 增大时,超空泡航行体将不能保持稳定航行的运动状态,出现周期振荡。在空化数 σ∈[0.024 25,0.031 78] 内任取 σ = 0.027,经计算得系统的平衡点 S2:[2.271 6,0,0.028 7,0.061 3]。在平衡点处获得系统(2)的 Jacobi 矩阵:
| $ { J{ s}_2}\!\!=\!\!\left[ \!{\begin{array}{*{20}{c}} \!\!\!{353.88}\!\!\! & \!\!\!{397.28}\!\!\! & \!\!\!{31303.26}\!\!\! & \!\!\!{-15651.63}\\ \!\!\!{-413.03}\!\! & \!\!{-256.10}\!\! & \!\!\!{-24996.18}\!\!\! & \!\!\!{12498.10}\!\!\\ 0 & 1 & 0 & 0\\ 1 & 0 & {-79.06} & 0 \end{array}} \!\!\right]\text{。} $ |
计算得到 4 个特征根为:λ1,2 = 67.159 ± j336.361,λ3,4 =-18.271 ± j32.222,其中特征根 λ1,2 是实部为正的共轭虚根,根据分叉理论,此时系统已经历 hopf 分叉,致使上述平衡态失稳,产生周期振荡。
相轨图是系统运动轨迹的记录,反映系统状态的变化情况,是观察系统中动力学行为的最直接的方法[10]。图 5 给出了系统(2)的一些典型的周期轨道,由图所示,极限环的出现说明系统发生了周期性振荡,极限环与临界切换分界线 w = wth 相交,航行体的垂直速度 w 时而大于 wth,时而小于 wth,由式(4)可知,航行体尾翼相应地不时摆动与空泡碰触,引起航行体滑行力周期性的变化,称为“尾击现象”[5]。表明系统映射从一个有界点逐步形成了不稳定的闭合极限环。
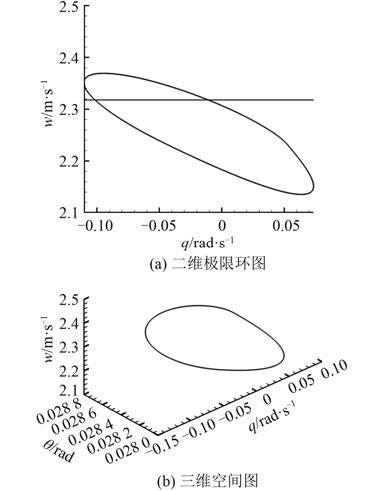
|
图 5 σ = 0.027 0 时系统相轨图 Fig. 5 Phase track diagram for σ = 0.027 0 |
由图 6 可知,航行体的 4 个状态变量水中深度 z、纵向速度 w、俯仰攻角 θ 以及角速度 q 均围绕平衡点 S2 位置发生周期性的微幅振荡。航行体尾部伸出空泡的长度 h′ 约在 [0,0.06] m 之间作周期振荡,表明此时航行体尾部不断与空泡壁面发生碰撞,尾翼时而处于空泡内部,不与空泡接触,滑行力为 0;时而穿过空泡深入水中,产生滑行力,相应的滑行力 Fplaning 在 [0,37] N 之间作周期振荡。由此也表明,此时航行体处于不稳定的周期运动状态,验证了上节对系统运动状态分析的正确性。系统持续的振荡不仅会影响控制设备的使用寿命,也会使控制精度下降,因此必须对航行体进行有效的控制避免周期振荡的发生。
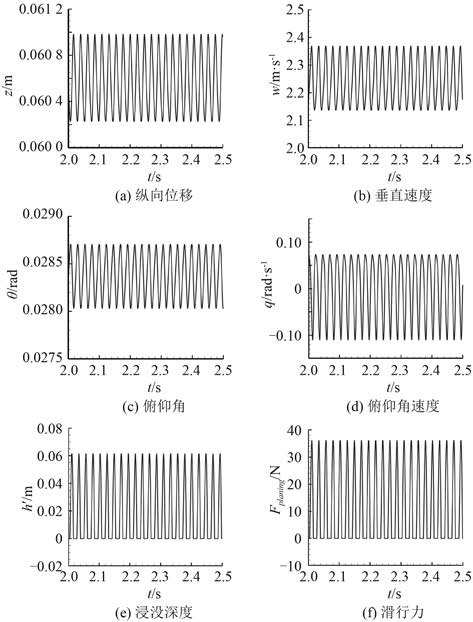
|
图 6 σ = 0.027 0 时系统响应示意图 Fig. 6 Time response for σ = 0.027 0 |
在随着 σ 逐步增大,系统历经一系列的倍周期分岔突变到混沌状态,在空化数范围 [0.031 78,0.036 0] 内任取 σ = 0.032 5,获得系统的平衡点 S3:[1.138 9,0,0.015 8,0.035 0],此时系统的 Jacobi 矩阵为:
| $ { J{ s}_3}\!\!=\!\!\left[ \!{\begin{array}{*{20}{c}} \!\!\!{902.74}\!\!\! & \!\!\!{338.27}\!\!\! & \!\!\!{26145.05}\!\!\! & \!\!\!{-13072.53}\!\!\!\!\\ \!\!\!{-1061.92}\!\!\! & \!\!\!{-214.40}\!\!\! & \!\!\!{-20877.27}\!\! & \!\!\!{10438.64}\!\!\!\\ 0 & 1 & 0 & 0\\ 1 & 0 & {-72.06} & 0 \end{array}} \right]\!\text{。} $ |
解得相对应的 4 个特征根为:λ1,2 = 365.839 ± j306.982,λ3,4 =-21.666 ± j30.46,这里,λ1,2 为实部为正共轭虚根,故平衡点 S3 为不稳定鞍焦点,即指数 2 平衡点,满足形成混沌吸引子的必要条件[10]。
图 7 给出了 σ = 0.032 5 系统相轨图在二维空间和三维平面上的投影.由图可知,此时系统的极限环演变形成了混沌吸引子,出现了混沌现象,此时航行体运动具有复杂的非线性动力学行为。
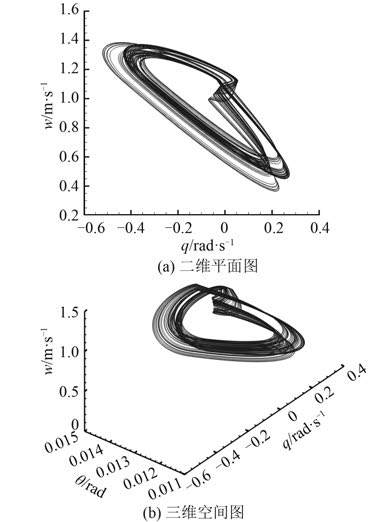
|
图 7 σ = 0.032 5 时系统相轨图 Fig. 7 Phase track diagram for σ = 0.032 5 |
由图 8(a)~图 8(d)可知,系统的 4 个状态变量 z,w,θ,q 随着时间的变化发生了剧烈的非周期震荡。同时,由图 8(e)~图 8(f)可看出,航行体尾部伸出空泡长度 h′ 与滑行力 Fplaning 也在随时间不断变化,浸没深度最高达到了 0.16 m,该长度超过了航行体的直径,对应的滑行力接近 300 N,显然,这种现象在实际运动中不可能出现,航行体已失去稳定进而倾覆,因此必须对航行体进行有效的控制以避免这种状况的发生。
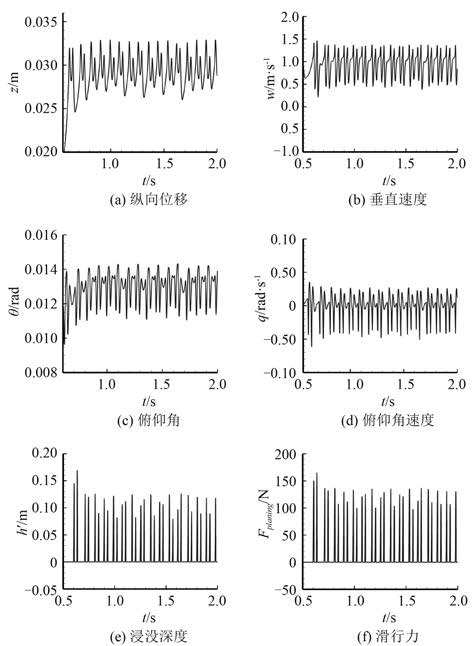
|
图 8 σ = 0.032 5 时系统响应示意图 Fig. 8 Time response for σ = 0.032 5 |
由上述分析可知,当超空泡航行体在经典控制率 δe = 0、δc = 15z-30θ-0.3q 下稳定航行的范围是空化数 σ∈[0.020,0.024 2],而在空化数的有效范围 σ∈[0.024 2,0.036 8] 下无法实现稳定航行,这是由于尾翼偏转角 δe = 0,往往会使航行体缺乏尾翼提供的支持力,不能平衡航行体的重力,从而导致航行体在重力的作用下浸入空泡而失稳,很大程度上限制了航行体的可控性以及稳定性。
为实现超空泡航行体稳定运动,保持空化器偏转角 δc 不变,调整尾翼偏转角 δe = kθ,其中 k 为俯仰角 θ 的反馈增益。依照分叉理论,图 9 给出了(σ,k)二维分岔图,揭示了在整个空化数有效范围内,反馈增益 k 的变化对航行体运动状态的影响。

|
图 9 系统动力学行为分布图 Fig. 9 Regions of different dynamical behaviors in the space of the bifurcation parameters σ and k |
参数 σ、k 同时变化时,在(σ,k)相空间上,其动力学行为分布情况如图 9 所示,水平切面是空化数 σ 变化时系统的分岔图,竖直切面是参数 k 变化时系统的分岔图。图中白色部分表示航行体稳定运动区域,在此区域内任意选取一点(σ, k),其空化数下对应的控制增益能够实现航行体的稳定航行;灰色部分则表示航行体不稳定运动区域,在此范围内航行体则会出现振动与冲击,处于不稳定状态。利用二维分岔图能够确定航行体稳定运动条件和参数取值范围,由此不难看出,空化数 σ∈[0.019 8,0.035 6] 时,在 [-7.5,31.5] 范围内调节控制增益 k 的取值,均能够有效实现超空泡航行体的稳定航行,大大地拓宽了系统稳定运动的范围,对航行体的稳定性控制具有指导意义。
4 结 语为研究水下超空泡航行体的运动特性,本文基于超空泡航行体的四维动力学模型,分析了不同空化数下航行体的运动状态,揭示了尾翼偏转角反馈控制增益的变化对航行体稳定性的影响,得到以下结论:
1)运用分叉理论可以确定超空泡航行体在任一参数下的运动稳定性,为探讨求解超空泡的非线性问题,提供了分析途径;
2)随着空化数的变化,超空泡航行体的运动具有稳定、周期和混沌 3 种状态;相轨图揭示了极限环和混沌吸引子的出现,说明超空泡航行体的纵向运动具有非线性动力学特性;
3)二维分岔图能够确定航行体稳定运动条件和参数范围,根据航行体的运动速度,可以对应设置恰当的控制率,从而有效抑制航行体的振动与冲击,实现超空泡航行体的稳定航行。
| [1] |
熊天红, 易文俊, 吴军基, 等. 小攻角下水下高速航行体超空泡流特性研究[J]. 舰船科学技术 , 2009, 31 (5) :27–30.
XIONG Tian-hong, YI Wen-jun, WU Jun-ji, et al. Investigation on characteristic of supercaviting flow around underwater highspeed vehicle at small angle of attack[J]. Ship Science and Technology , 2009, 31 (5) :27–30. |
| [2] | SAVCHENKO Y N. Supercavitation-problems and perspectives[C]//Proceedings of the fourth international symposium on cavitation. Pasadena, California:California Institute of Technology, 2001:1-8. |
| [3] |
朱新坚, 邵惠鹤, 张钟俊. 一类非线性系统Hopf分叉的控制[J]. 上海交通大学学报 , 1997, 31 (6) :52–55.
ZHU Xin-jian, SHAO Hui-he, ZHANG Zhong-jun. Control of Hopf bifurcation in a certain nonlinear system[J]. Journal of Shanghai Jiaotong University , 1997, 31 (6) :52–55. |
| [4] |
魏英杰, 王京华, 张嘉钟, 等. 水下超空泡航行体非线性动力学与控制[J]. 振动与冲击 , 2009, 28 (6) :179–182.
WEI Ying-jie, WANG Jing-hua, ZHANG Jia-zhong, et al. Nonlinear dynamics and control of underwater supercavitating vehicle[J]. Journal of Vibration and Shock , 2009, 28 (6) :179–182. |
| [5] | LIN G J, BALACHANDRAN B, ABED E H. Bifurcation behavior of a supercavitating vehicle[C]//Proceedings of the 2006 ASME international mechanical engineering congress and exposition. Chicago, Illinois, USA:ASME, 2006. |
| [6] |
白涛, 孙尧, 莫宏伟. 分叉分析在水下高速运动体稳定控制中的应用[J]. 哈尔滨工程大学学报 , 2008, 29 (10) :1067–1075.
BAI Tao, SUN Yao, MO Hong-wei. Application of bifurcation analysis to the stability control of underwater high-speed vehicles[J]. Journal of Harbin Engineering University , 2008, 29 (10) :1067–1075. |
| [7] | DZIELSKI J, KURDILA A. A benchmark control problem for supercavitating vehicles and an initial investigation of solutions[J]. Journal of Vibration and Control , 2003, 9 (7) :791–804. DOI:10.1177/1077546303009007004 |
| [8] | 张宇文, 袁绪龙, 邓飞. 超空泡航行体流体动力学[M]. 北京: 国防工业出版社, 2014 : 3 -25. |
| [9] |
许多生, 陆启韶. 飞机滚转时惯性耦合运动的分岔分析[J]. 航空学报 , 2001, 22 (2) :144–147.
XU Duo-sheng, LU Qi-shao. Bifurcation analysis of inertia cross coupling in aircraft rolling[J]. Acta Aeronautica et Astronautica Sinica , 2001, 22 (2) :144–147. |
| [10] | 包伯成. 混沌电路导论[M]. 北京: 科学出版社, 2013 : 3 -39. |
| [11] | LIN G J, BALACHANDRAN B, ABED E H. Dynamics and control of supercavitating vehicles[J]. Journal of Dynamic Systems, Measurement, and Control , 2008, 130 (2) :021003. DOI:10.1115/1.2837307 |
| [12] |
易文俊, 熊天红, 刘怡昕. 水下高速射弹超空泡形态特性的数值模拟研究[J]. 舰船科学技术 , 2008, 30 (4) :117–121.
YI Wen-jun, XIONG Tian-hong, LIU Yi-xin. Numerical simulated research on characteristic of supercavity form around underwater high-speed projectile[J]. Ship Science and Technology , 2008, 30 (4) :117–121. |
 2016, Vol. 38
2016, Vol. 38
