0 引言

进入21世纪，随着舰船装备复杂程度的不断提高，与装备测试和诊断能力息息相关的测试性设计要求日益增加，测试性设计已被提高到与可靠性、维修性设计同等重要的地位^[1-2]。近几年，在我国舰船装备的研制过程中就明确提出了故障检测率、故障隔离率以及诊断策略等测试性设计要求，而开展测试性建模与分析则是进行诊断策略设计分析以及测试性指标预计的有效手段^[3-4]。目前，装备的测试性建模理论层出不穷，建模方法日新月异，如测试性定量模型、测试性定性模型、功能角色图模型、有向图模型、键合图模型、混合诊断模型、行为以太网模型、贝叶斯网络模型等^[5-7]。这些模型虽然在理论上均可用于产品的故障诊断，但对于复杂舰船产品的测试性建模与分析指导性不强，因为对于复杂舰船产品来说不仅要求明确其每个组成单元的每个故障都能被何种测试所检测，同时也要求明确每个测试都能检测到哪些组成单元的哪些故障，因此能够同时满足上述要求的最简单测试性模型只有信息流模型^[8-9]。信息流模型的概念是由美国人De Paul于20世纪60年代提出，并将其应用于美军武器装备的测试性设计、诊断策略设计、可靠性维修性设计等领域，为美军装备的诊断策略和指标预计等工作提供了较好的技术基础^[10]。

本文提出一种以信息流为表征的基于任务的测试性建模与分析方法，并结合某舰船电力系统的典型任务进行测试性建模、诊断树建立及测试性预计的举例研究，为舰船装备测试性建模与分析应用研究提供新思路。

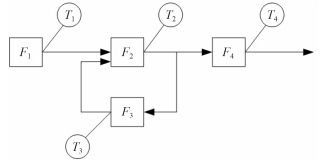
1 基于任务的测试性建模 1.1 信息流建模理论

信息流模型是在产品的任务和结构合理划分之后，在产品任务模型的基础上，清晰表明任务信息流方向和各功能部件相互连接关系，并以此表明各功能部件与各测试点关系的一种测试性模型^[11]，具有内在的简单化特点。信息流模型分为图示模型和数学模型2种，其中图示模型的作用是用有向图来表示测试与测试、测试与诊断结果之间的连接关系，如图 1所示，其中方框代表测试单元（功能部件），圆圈代表测试点，箭头表明了功能信息传递的方向。

数学模型的作用是在图示模型的基础上用矩阵形式来描述单元与测试之间的相关性，以分析出系统中哪些故障不可测、哪些测试冗余、哪些故障构成了模糊组，进而可建立故障诊断树和生成诊断策略。信息流数学模型可用下述矩阵来表示：

$ {{\boldsymbol D}_{m\times n}}=\left[ \begin{align} & {{d}_{11}}\text{ }{{d}_{12}}\text{ }\cdots \text{ }{{d}_{1n}} \\ & {{d}_{21}}\text{ }{{d}_{22}}\text{ }\cdots \text{ }{{d}_{2n}} \\ & \text{ }\vdots \text{ }\vdots \text{ }\vdots \\ & {{d}_{m1}}\text{ }{{d}_{m2}}\text{ }\cdots \text{ }{{d}_{mn}} \\ \end{align} \right] \text{，} $

(1)

其中第i行矩阵

$ {{F}_{i}}=[{{d}_{i1}}{{d}_{i2}}\cdots {{d}_{in}}] \text{，} $

(2)

表示第i个测试单元（功能部件）的故障在各个测试点上的反应信息，它表明了F_i和测试点T_j（j=1，2，…，n）的相关性。而第j列矩阵

$ {{T}_{j}}={{[{{d}_{1j}}{{d}_{2j}}\cdots {{d}_{mj}}]}^{\rm T}}\text{，} $

(3)

则表示第j个测试点可测得的各测试单元（功能部件）的故障信息。它表明了T_j与各测试单元（功能部件）F_i（i=1，2，…，m）的相关性。其中，当T_j可测得F_i故障信息时（即T_j与F_i相关），d_ij=1；当T_j不能测得F_i故障信息时（即T_j与F_i不相关），d_ij=0。信息流数学模型也称为产品D矩阵模型，采用直接分析法或一阶相关性列矢量法可基于图 1所示的信息流图示模型转化为式（4）所示的数学模型。

$ \begin{array}{l} \begin{array}{*{20}{c}} {{{\begin{array}{*{20}{c}} {}&T \end{array}}_1}}&{{T_2}}&{{T_3}}&{{T_4}} \end{array}\\ \begin{array}{*{20}{c}} {{F_1}}\\ {{F_2}}\\ {{F_3}}\\ {{F_4}} \end{array}\left[ {\begin{array}{*{20}{c}} 1&1&1&1\\ 0&1&1&1\\ 0&1&1&1\\ 0&0&0&1 \end{array}} \right]. \end{array} $

(4)

1.2 基于任务的测试性建模

基于任务的测试性模型是一种以信息流模型为表征的产品测试性建模与方法，已广泛应用于武器装备的测试与故障诊断、系统工程、可靠性设计等领域^[12]。基于任务的测试性建模主要流程包括产品功能框图建立、以故障分析为引导的模型精简和细化、基于信息流的图示模型建立、产品D矩阵模型（信息流数学模型）建立、D矩阵模型简化、优化测试点、诊断树建立和测试性预计等，如图 2所示。其中基于任务的图示模型是建立D矩阵模型的基础，它是在以故障分析为引导的产品精细化任务模型基础上建立的，清晰表明了产品功能信息流的方向和各设备之间的相互连接关系，并清晰标注了产品初选测试点的位置和编号，以此标识各设备与测试点的相互关系；而简化后的D矩阵模型则是建立故障诊断树的基础，它是根据基于任务的图示模型采用直接分析法或通过一阶相关性列矢量法求解，并通过矩阵的行列对比进行简化后得到的，对于故障诊断结果有着直接影响。

需要说明的是，为便于基于任务的信息流图示模型建立，通常应对被测产品做如下假设：

1）被测产品中的各功能部件只有正常和故障2种状态，处于故障状态时功能部件不能工作；

2）当被测产品中某个功能部件处于故障状态时，设定其发生的为单故障；

3）被测产品的状态完全取决于其各功能部件的状态，即某一功能部件处于故障状态时，在模型信息流可以到达的产品内部各个测试点上，其测量的有效性都一样。

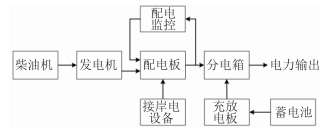
2 舰船电力系统测试性建模与分析举例 2.1 建立任务模型

电力系统是舰船装备的重要一级系统，可为全船提供航行、训练、作战以及设备日常所需的全部电力载荷。假设某水面舰船的电力系统包括电站（柴油机、发电机）、配电板、配电监控、分电箱、蓄电池、充放电板、接岸电设备等，根据其运行特点可建立典型任务模型如图 3所示。

2.2 以故障分析为引导精简和细化模型

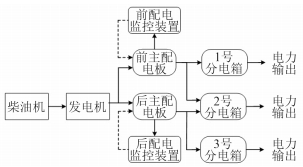
故障模式影响分析（FMEA）是进行产品任务模型精简和细化的有效途径，通过对产品各功能部件进行功能故障分析，可剔除重要程度相对较低的部件，并可对重要程度较高的部件组成或功能模式进行细化，以获得更加准确的产品典型任务模型。由于某舰船电力系统的典型任务中包括电站供电、岸电供电和应急供电3种任务模式，对其进行FMEA后可知电站供电为其中最重要的任务模式，因而根据此分析结果可对典型任务模型进行精简和细化，将重要程度相对较低的接岸电设备、充放电板和蓄电池等剔除，同时根据系统实际组成细化配电板、配电监控和分电箱等重要单元部件，可得精简和细化后的电力系统典型任务模型如图 4所示。

同时，可将电力系统典型任务描述如下：柴油机带动发电机运转产生电流，并同时将电力供应给前、后主配电板，而前、后主配电板又将电力供应分配至1，2，3号分电箱，通过分电箱将电力供应输送给舰上的用电设备。此外，前、后配电监控装置分别由前、后主配电板供电并对其进行监控。

2.3 建立信息流模型

根据精简和细化后的电力系统典型任务模型所表示的设备连接关系和信号传输方向，分别用F₁，F₂，F₃，F₄，F₅，F₆，F₇，F₈，F₉来标识柴油机、发电机、前主配电板、前配电监控装置、后主配电板、后配电监控装置和1，2，3号分电箱，可得此时电力系统基于任务的信息流图示模型如图 5所示，图中T₁，T₂，T₃…T₁₀等代表初选测试点的位置。

由于该电力系统的信息流图示模型相对简单，可采用直接分析法对其进行分析，建立电力系统的信息流数学模型（以下简称“D矩阵模型”）如表 1所示，其中测试点输出正常用“0”表示，不正常用“1”表示。

由表 1可见，列T₂和T₃、列T₄和T₅列、T₆和T₇两两相同，表明在图示模型中测试点3，5，7的测试功能与2，4，6相同，因而说明测试点3，5，7属于冗余设置，可以去掉；而行F₃和F₄、行F₅和F₆两两相同，说明F₃和F₄、F₅和F₆在各自的反馈回路内是1个模糊组，在此条件下不能区分是谁的故障，因此合并表中相同的行和列，可得简化后的D矩阵模型如表 2所示。

2.4 优选测试点 2.4.1 选择检测用测试点

由于简化后的电力系统D矩阵模型为D=[d_ij]_{m ×n}形式，因而第j个测试点的故障检测权值W_FDj（提供故障检测有用信息多少的相对度量）可用式（5）计算，并可将计算结果列于表 2的最后一行：

$ {W_{FDj}} = \sum\limits_{i = 1}^m {{d_{ij}}} \quad \text{，} \quad \quad m = 7,{\rm{ }}j = 1,2, \cdots ,10 \text{，} $

(5)

计算出各测试点的W_FD之后，选用W_FD值最大的测试点T₉作为第1个检测用测试点，并选取其对应的列矩阵为T₉，如式（6）所示。而再用T₉分割D矩阵后，可得${\boldsymbol D}_{1}^{0}$、${\boldsymbol D}_{1}^{1}$两个子矩阵如式（7）和式（8）所示。

$ {T_9} = {[1\,\,{\rm{ 1 \,\, 1 \,\, 1 \,\, 0 \,\, 1 \,\, 0}}]^{\rm T}} \text{，} $

(6)

$ {\boldsymbol D}_1^0 = \left[ {\begin{array}{*{20}{c}} 0& 0 & 0 & 0 & 1 & 0 & 0\\ 0& 0 & 0 & 0 & 0 & 0 & 1 \end{array}} \right] = \left[ \begin{array}{l} {F_7}\\ {F_9} \end{array} \right] \text{，} $

(7)

$ {\boldsymbol D}_1^1 = \left[ {\begin{array}{*{20}{c}} 1 & 1 & 1 & 1& 1 & 1 & 1\\ 0 & 1 & 1 & 1& 1 & 1 & 1\\ 0 & 0 & 1 & 0& 1 & 1 & 0\\ 0 & 0 & 0 & 1& 0 & 1 & 1\\ 0 & 0 & 0 & 0& 0 & 1 & 0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{F_1}}\\ {{F_2}}\\ {{F_3}\text{，}\!\!{F_4}}\\ {{F_5}\text{，}\!\!{F_6}}\\ {{F_8}} \end{array}} \right] \text{。} $

(8)

由式（7）和式（8）可见，${\boldsymbol D}_{1}^{1}$有5行，而${\boldsymbol D}_{1}^{0}$只有2行，且${\boldsymbol D}_{1}^{0}={{\left[ \begin{matrix} {{F}_{7}} & {{F}_{9}} \\ \end{matrix} \right]}^{\text{ }{\rm T}}}$。由此可以表明，在对电力系统进行故障检测时，首先检测T₉，即可判断是F₇或F₉发生的故障还是除此2个单元之外部分的故障。又由于${{\left[ \begin{matrix} {{F}_{7}} & {{F}_{9}} \\ \end{matrix} \right]}^{\rm T}}$中W_FD值最大者均为1，即T₈和T₁₀的W_FD值均为1，若在测出T₉无故障的情况下，再分别测得T₈和T₁₀也无故障，则可表明整个电力系统无故障。

2.4.2 选择隔离用测试点

由于简化后的电力系统D矩阵模型为D=[d_ij]_{m ×n}形式，因而第j个测试点的故障隔离权值W_FIj（提供故障隔离有用信息多少的相对度量）可用式（9）计算，并可将计算结果列于表 3的最后一行：

$ {W_{FIj}} = \sum\limits_{i = 1}^Z {(N_j^1N_j^0)} \text{，}\quad \quad {{j = 1}},{\rm{2}}, \cdots ,{\rm{10}} \text{。} $

(9)

式中：$N_{j}^{1}$为列矩阵T_j中元素为1的个数；$N_{j}^{0}$为T_j中元素为0的个数；Z为分割后的矩阵数。

根据前述内容已知，W_FD值最大的测试点为T₉，因此选择第1个隔离用测试点为T₉，其列矩阵分割出来的${\boldsymbol D}_{1}^{0}$，${\boldsymbol D}_{1}^{1}$如表 3所示，且可计算出第1次分割后的W_FI值，并选择W_FI值最大者为第2个隔离用测试点。由于此时${\boldsymbol D}_{1}^{0}={{\left[ \begin{matrix} {{F}_{7}} & {{F}_{9}} \\ \end{matrix} \right]}^{\rm T}}$，仅有2行，且有2个W_FI值最大者，即T₈和T₁₀，任取其中之一，即可隔离出是F₇还是F₉故障。本文取T₈作为第2个隔离用测试点，对${\boldsymbol D}_{1}^{1}$进行分割，将其分割为${\boldsymbol D}_{2}^{0}$、${\boldsymbol D}_{2}^{1}$并计算得到第2次分割后的W_FI值。而第2次分割后的W_FI值最大者为T₆和T₁₀，则任取其中之一T₁₀为第3个隔离用测试点。由于此时${\boldsymbol D}_{2}^{0}$只有2行，再进行1次分割即可成为单行，因而通过T₁₀即可隔离出其故障，而${\boldsymbol D}_{2}^{1}$则可被分割为${\boldsymbol D}_{3}^{0}$，${\boldsymbol D}_{3}^{1}$，并可得到第3次分割后的W_FI值。由于此时${\boldsymbol D}_{3}^{0}$=F₃F₄，只有1行，不用考虑；而${\boldsymbol D}_{3}^{1}$只有2行，利用第3次分割后W_FI值最大者T₁即可隔离出其故障。综上所述，T₉、T₈、T₆和T₁即为电力系统依次选用的故障隔离用测试点，如表 3所示。

2.5 建立诊断树

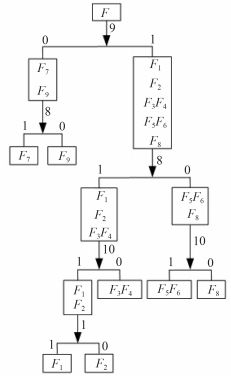
根据表 3所示D矩阵模型和隔离用测试点的优选结果，当第1个隔离用测试点T₉的测试结果为0时，说明系统故障发生在F₇或F₉；为1时，说明故障发生在F₁，F₂，F₃F₄，F₅ F₆和F₈之中。再用第2个隔离用测试点T₈测试，如结果为1，则故障发生在F₇或者F₁，F₂和F₃F₄之中。再用第3个隔离用测试点T₁₀测试，如结果为0，则可判断为F₃F₄故障；如结果为1，则故障在F₁，F₂之中。同理，再用第4个隔离用测试点用T₁测试，如结果为0，则可判断为F₂故障；如结果为1，则可判断为F₁故障。同理，若在刚才的测试中T₈的结果为0，则故障在F₉或者F₅F₆、F₈之中。再用T₁₀测试，如结果为0，则可判断为F₈故障；如结果为1，则可判断为F₅F₆故障。把上述分析过程用图形表示出来，即可得到电力系统的故障诊断树如图 6所示。

2.6 测试性预计

故障诊断树可用于确定产品的诊断策略，也可用于初步预计产品的故障检测率、故障隔离率等测试性指标，其计算公式如下：

$ {\gamma _{{ }_{FD}}} = \frac{{{U_{{ }_{FD}}}}} {{{U_{{ }_{T}}}}} \times 100\% \text{，} $

(10)

$ {\gamma _{{ }_{FI}}} = \frac{{{U_{{ }_{FI}}}}}{{{U_{{ }_{FD}}}}} \times 100\% \text{，} $

(11)

式中：γ_FD为故障检测率；γ_FI为故障隔离率；U_FD为测试点能够检测到的组成单元数量；U_FI为测试点能够隔离出的组成单元（或模糊组）数量；U_T为系统组成单元总数。

将表 3和图 5结果代入式（10）和式（11），可初步预计该典型任务下的电力系统故障检测和隔离能力为：

$ {\gamma _{{ }_{FD}}} = \frac{9}{9} \times 100\% = 100\% \text{，} $

(12)

$ {\gamma _{{ }_{FI}}} = \frac{7}{9} \times 100\% = 78\% \text{。} $

(13)

3 结语

测试性建模与分析是进行诊断策略设计和测试性指标预计的有效手段，本文提出一种基于任务的舰船产品测试性建模与分析方法，通过建立产品基于任务的图示信息流模型求解产品的D矩阵模型，进而建立产品诊断树和进行测试性预计，并为确定诊断策略提供依据。同时，选取某舰船电力系统，建立其典型任务模型，并在此基础上进行了基于任务的测试性建模、诊断树建立及测试性预计举例，结果表明该方法具有直观、高效的建模和预计功能，为舰船装备的测试性建模、分析和诊断策略研究提供了新思路。