2. 江苏科技大学, 江苏 镇江 212003
2. Jiangsu University of Science and Technology, Zhenjiang 212003, China
导弹等水下航行体从水下一定深度的发射筒内,利用燃气向水面垂直发射。航行体出筒后发射筒内高温高压的燃气会涌出发射筒,在海水中形成脉动压力场,并与筒盖结构以及航行体尾部交互耦合作用。这种脉动的筒口压力场将会对发射筒盖等结构强度形成不利影响[1, 2]。
针对筒口气泡脉动形态和压力预示,目前常采用理论计算和数值CFD模拟2种方法开展研究。在理论计算方面,王诚等[3]采用一维非定常气流场模型和轴对称理想水流场模型,对水下发射导弹的尾部非定常燃气泡内外流场进行耦合数值求解,计算了燃气泡发展对导弹所受水动力的影响。李杰等[4]采用Rayleigh-Plesset方法,建立压球状尾空泡模型,研究了空泡对弹道的影响。程少华等[5]结合空泡独立膨胀原理和Rayleigh-Plesset方程,建立了导弹尾空泡非定长发展数学模型,对弹尾空泡和压力进行预示。
在数值CFD模拟方面,王汉平等[6-7]基于VOF模型和动网格技术对潜射导弹出筒筒口压力场特性进行了二维和三维仿真分析。邱海强、王亚东等[8-9]利用Mixture多项流模型和动网格技术,对导弹弹射出筒筒口气泡的发展情况进行研究,并重点关注了筒口气泡对发射艇表面压力脉动的影响。
本文采取刚体Lagrange结构网格和Euler流场网格(L/E)耦合的方法[10-11]开展筒口压力场三维数值仿真计算。计算模型考虑航行体出筒过程对筒口流场的扰动和横向来流对筒口压力场的影响。
1 控制方程及数值方法 1.1 控制方程流体运动采用Euler方法模拟,建立流体欧拉域。控制方程包括质量、动量和能量守恒。
质量守恒:
| $ \frac{\partial }{{\partial t}}\iiint\limits_{vol} {\rho {\rm d}V} = - \iint\limits_{surf} {\rho (u \cdot n){\rm d}A} \text{;} $ |
动量守恒:
| $ \begin{array}{l} \displaystyle\int \!\!\!{\int\limits_{vol}\!\!\! {\int {\rho {u_i}{\rm d}V} } } + \int \!\!\! {\int\limits_{surf} {\rho {u_i}(u \cdot n){\rm d}A = - } } \\ \quad \quad \quad \quad \quad \displaystyle\int\!\!\! {\int\limits_{surf} {p{n_i}{\rm d}A + \int \!\!\! {\int\limits_{surf} {{s_{ij}}{n_i}{\rm d}A} } } } \text{;} \end{array} $ |
能量守恒:
| $ \frac{\partial }{{\partial t}}\iiint\limits_{vol} {\rho e{\rm d}V} + \iint\limits_{surf} {\rho e(u \cdot n)} {\rm d}A = - \iint\limits_{surf} {{u_i}p{n_i}} {\rm d}A\text{。} $ |
式中:ρ为材料密度;ui为速度分量;p为压力;sij为粘性偏应力张量;e为比内能。
1.2 状态方程状态方程定义各种不同状态下的压力和密度以及比内能之间的函数关系。对于海水,采用多项式状态方程。
压缩状态(μ > 0):
| $ p \!=\! {a_1}\mu \!+\! {a_2}{\mu ^2} \!+\! {a_3}{\mu ^3} \!+\! ({b_0} + {b_1}\mu \!+\! {b_2}{\mu ^2} \!+\! {b_3}{\mu ^3}){\rho _0}e\text{,} $ | (1) |
拉伸状态(μ < 0):
| $ p = {a_1}\mu + ({b_0} + {b_1}\mu ){\rho _0}e\text{。} $ | (2) |
其中
对于燃气采用Gamma状态方程:
| $ p = (\gamma - 1)\rho e\text{。} $ | (3) |
式中:e为燃气比内能;ρ为燃气密度;比热比γ=1.2。
1.3 耦合算法本计算中包括固体域和流体域2个计算域。固体域主要模拟航行体,采用Lagrange方法模拟,Lagrange网格设置为刚体模拟航行体运动,但不发生变形。流体域包括海水和燃气所填充的Euler网格区域,采用Euler方法模拟。2个计算域相互重叠。为了使固体域和流体域间产生相互作用,在Lagrange网格结构外部定义一封闭耦合面,用于传递2种解算器之间的力。此耦合面对Euler网格来说是一种流动边界,材料在Euler网格中流动产生的压力通过耦合面传到Lagrange结构上,使结构发生运动或变形;Lagrange结构运动或变形也反过来影响Euler材料的流动和压力值。
2 计算模型 2.1 航行体模型航行体沿轴线建立一半对称模型,头部采用双曲线头型,如图 1所示。航行体设置为刚体,除了垂直向上的运动外,其余5个自由度固定。航行体筒内和出筒运动的轨迹已有较为精确的计算数据,直接加载到航行体上。航行体圆柱段直径为Dm,总长为7Dm。

|
图 1 航行体模型 Fig. 1 Model of vehicle |
由于流体域相对于过轴线的海水横向流流动方向对称,为减小计算量,建立对称流体域计算模型。取发射筒口中心为坐标原点,海水流场区域为半圆柱,半径5.6Dm,深22Dm。海水区域下为发射筒流场,按照航行体尺寸建立。
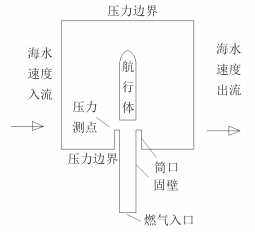
计算区域及边界条件如图 2所示。流场区域上下为压力边界,左右为海水速度入口和出口边界,最底部为燃气入口边界,其他为固体边界。
|
图 2 计算域及边界条件 Fig. 2 An outline of the computational domain with boundary conditions |
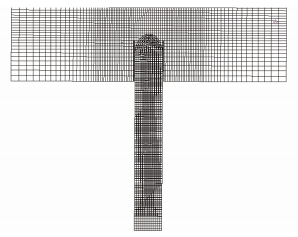
计算流场区域网格如图 3所示。对航行体运动区域和筒口压力场作用区域网格进行加密。初始时刻模拟航行体的Lagrange计算网格与发射筒流场区域的Euler网格重叠(见图 4)。Lagrange固体网格表面为流体-固体耦合面,计算中耦合面内重叠区域Euler网格材料自动为空。

|
图 3 流场计算网格 Fig. 3 Mesh of fluid field |
|
图 4 耦合计算固体与流体重叠网格 Fig. 4 Overlap mesh of solid and fluid field in coupling simulation |
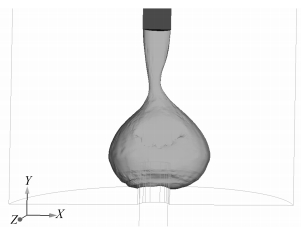
航行体离开发射筒前,发射筒内燃气封闭于发射筒与航行体组成的空腔内,压力高于周围海水压力。航行体尾部离开发射筒后,由于受压力及惯性等作用,筒内燃气向外扩张(见图 5),形成第1个压力峰。随着燃气在海水中的膨胀,燃气泡内的压力不断下降。由于惯性作用,在到达压力与外界压力平衡时,燃气泡将继续膨胀,气泡内的压力将小于气泡外界压力(见图 6),直到燃气泡压力达到最小极值停止膨胀。随后,由于燃气泡内外压力不平衡,燃气泡开始收缩。

|
图 5 航行体出筒燃气压力膨胀 Fig. 5 Gas bubble inflate after the vehicle leave the canister |
|
图 6 筒口燃气过膨胀 Fig. 6 Gas bubble over inflate |
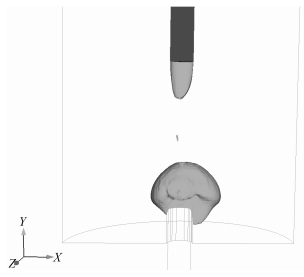
由于惯性作用,燃气泡压力将超越与海水环境压力等值点继续升高,直到达到第2个压力峰值,在此过程中部分燃气随航行体尾部与主脉动气泡分离(见图 7)。此后燃气泡持续脉动,一部分能量在海水环境中耗散,一部分能量随燃气泡上升过程带走。此过程与水下爆炸压力场脉动特征相近。由计算结果可以看出,由于计算中考虑了横向海流,筒口气泡在脉动过程中出现了向X正向的飘移。
|
图 7 筒口燃气泡航行体尾部气泡分离 Fig. 7 Vehicle bottom bubble separate from the canister outlet gas bubble |
将海水速度入口和海水速度出口边界条件改为压力边界条件,并将海水初始速度赋值为0,开展无横向流筒口压力场计算。在此工况下,筒口气泡在脉动过程中没有出现向X正向的飘移(见图 8)。
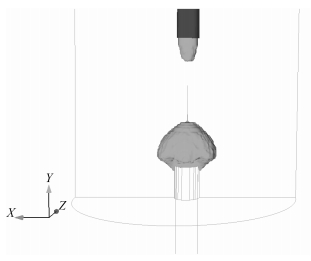
|
图 8 筒口燃气泡航行体尾部气泡分离(无横流) Fig. 8 Vehicle bottom bubble separate from the canister outlet gas bubble (no lateral flow) |
图 9给出了试验与含横向流计算的筒口压力曲线。图 10为试验与无横向流计算的筒口压力曲线。曲线X时间轴从航行体尾部出筒时刻开始。Y轴为测点压力与航行体出筒时刻筒内燃气压力的比值。由2组对比曲线可知,计算筒口压力曲线和试验压力曲线均呈现剧烈的压力脉动,随着时间推移压力脉动快速衰减。试验与计算的2个主要压力波峰曲线形状基本一致。
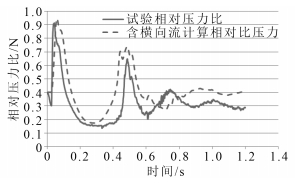
|
图 9 试验与含横向流计算筒口压力曲线对比 Fig. 9 Comparison between simulation curve (consider lateral flow) and test curve |
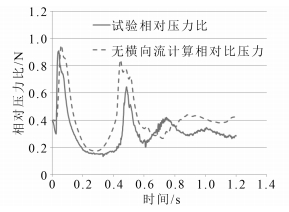
|
图 10 试验与无横向流计算筒口压力曲线对比 Fig. 10 Comparison between simulation curve (no lateral flow) and test curve |
取2个主要压力波峰极值作为特征点,对比计算与试验结果偏差(见表 1)。由表 1可知,计算结果相对于试验值均略为偏高。其中含横向流工况2个特征点的计算偏差为3.81%和14.3%,无横向流工况2个特征点的计算偏差为4.59%和30.1%。含横向流计算压力波峰值的偏差明显小于无横向流计算,特别是第2个波峰计算偏差减小至0.5倍以下。说明计算中考虑横向流作用可以有效减少筒口压力场计算偏差。
|
|
表 1 特征点计算值与试验值偏差统计 Tab.1 Statistics of characteristic value between simulation and test |
本文采用Lagrange结构网格和Euler流场网格耦合的方法,对潜射航行器出筒后筒口压力场进行三维数值仿真分析。由于计算模型考虑了海水的横向来流,筒口气泡在脉动中出现了随来流偏转的特征。试验与计算的2个主要压力波峰曲线形状基本一致。2个主要压力峰值特征点的计算偏差为3.81%和14.3%,可以满足工程研制需要。含横向流工况和无横向流工况计算偏差对比表明,计算中考虑横向流作用可以有效减少筒口压力场计算偏差。本文的建模方法和仿真结果对潜射航行器筒盖系统的受载分析以及筒盖系统结构设计,具有工程参考价值。
| [1] |
曾强.潜载导弹发射装置筒盖系统CAE研究[D].北京:北京理工大学, 1997.
ZENG Qiang. An CAE study on the cover system of submarine-borne missile launcher[D]. Beijing: Beijing Institute of Technology, 1997. |
| [2] |
王汉平, 余文辉, 赵恒, 等. 导弹筒盖系统的故障复现及结构改进[J]. 北京理工大学学报 , 2006, 26 (2) :107–111.
WANG Han-ping, YU Wen-hui, ZHAO Heng, et al. Fault replay and design modification of missile cover system[J]. Transactions of Beijing Institute of Technology , 2006, 26 (2) :107–111. |
| [3] |
王诚, 叶取源, 何友声. 导弹水下发射燃气泡计算[J]. 应用力学学报 , 1997, 14 (3) :1–7.
WANG Cheng, YE Qu-yuan, HE You-sheng. Calculation of an exhausted gas cavity behind an under-water launched missile[J]. Chinese Journal of Applied Mechanics , 1997, 14 (3) :1–7. |
| [4] |
李杰, 鲁传敬. 潜射导弹尾部燃气后效建模及数值模拟[J]. 弹道学报 , 2009, 21 (4) :6–8.
LI Jie, LU Chuan-jing. The model of combustion gas bubble of submarine-launched missile and numerical simulation[J]. Journal of Ballistics , 2009, 21 (4) :6–8. |
| [5] |
程少华, 权晓波, 王占莹, 等. 水下航行体垂直发射尾部空泡形态与压力预示方法研究[J]. 水动力学研究与进展A辑 , 2015, 30 (3) :299–305.
CHENG Shao-hua, QUAN Xiao-bo, WANG Zhan-ying, et al. Prediction method on trailing cavity shape and pressure of the underwater vehicle in vertical launching[J]. Chinese Journal of Hydrodynamics , 2015, 30 (3) :299–305. |
| [6] |
王汉平, 吴菊华. 基于CFD的潜射导弹筒口压力场预测[J]. 弹道学报 , 2008, 20 (4) :73–76.
WANG Han-ping, WU Ju-hua. Forecast of pressure field near launch canister outlet for underwater-launched missile based on CFD[J]. Journal of Ballistics , 2008, 20 (4) :73–76. |
| [7] |
王汉平, 余文辉, 魏建峰. 潜射模拟弹筒口压力场仿真[J]. 兵工学报 , 2009, 30 (8) :1009–1013.
WANG Han-ping, YU Wen-hui, WEI Jian-feng. Simulation of pressure field near canister outlet for underwater-launched emulated missile[J]. Acta Armamentarii , 2009, 30 (8) :1009–1013. |
| [8] |
邱海强, 袁绪龙, 王亚东, 等. 潜射导弹筒口气泡发展规律研究[J]. 兵工学报 , 2014, 35 (9) :1510–1514.
QIU Hai-qiang, YUAN Xu-long, WANG Ya-dong, et al. Research on the law of development of outlet cavity during the launch of submarine launched missile[J]. Acta Armamentarii , 2014, 35 (9) :1510–1514. |
| [9] |
王亚东, 袁绪龙, 覃东升. 导弹水下发射筒口气泡特性研究[J]. 兵工学报 , 2011, 32 (8) :991–995.
WANG Ya-dong, YUAN Xu-long, QIN Dong-sheng. Research on the outlet cavity features during the launch of submarine launched missile[J]. Acta Armamentarii , 2011, 32 (8) :991–995. |
| [10] |
吴国民, 周心桃, 李俊. 水下爆炸作用下固支平板动态响应分析[J]. 舰船科学技术 , 2013, 35 (4) :25–28.
WU Guo-min, ZHOU Xin-tao, LI Jun. Dynamical response of flat plates subjected to underwater explosion[J]. Ship Science and Technology , 2013, 35 (4) :25–28. |
| [11] |
张振华, 朱锡, 白雪飞. 水下爆炸冲击波的数值模拟研究[J]. 爆炸与冲击 , 2004, 24 (2) :182–188.
ZHANG Zhen-hua, ZHU Xi, BAI Xue-fei. The study on numerical simulation of underwater blast wave[J]. Explosion and Shock Waves , 2004, 24 (2) :182–188. |
 2016, Vol. 38
2016, Vol. 38
