UUV推进电机在前几年由于电子元器件的发展不成熟,影响了控制的精度,多采用直流电机,而直流电机在结构上有换向器和电刷,该部分使得电机的结构庞大,电机使用时影响整个控制系统效率低。随着电子元器件的发展成熟,控制算法也同样发展,使得永磁同步电机替代直流电机作为动力输入成为了一种趋势[1]。目前还没有人把这种和永磁同步电机结合的控制方法运用在水下航行体中,这一领域只是进行算法的理论研究,考虑电机的效率由电机本身的结构设计和控制器的控制算法所影响,所以需要注意2个方面:一是如何确定电机的结构设计达到了最优;二是设计出的电机需要和相应的控制器进行合理的匹配,以使整个驱动系统总的效率最大[2]。
1 系统控制策略本文不以电机的结构设计为主,重点关注控制算法的实现。永磁同步电机控制系统由TMS320F 28335作为主控部分,选用IPM为主驱动模块,光电隔离电路部分,电流检测和信号处理电路,保护电路构成。软件算法程序通过CCS实现,TMS320F28335控制芯片是目前已经使用比较成熟的2812芯片的升级。
2 PMSM驱动系统控制策略实现在Matlab 2010a中建立Foc控制系统(磁场定向控制)的simulink仿真模型,对控制算法的可能性进行验证,在算法得到验证的基础上再进行代码部分的编写。
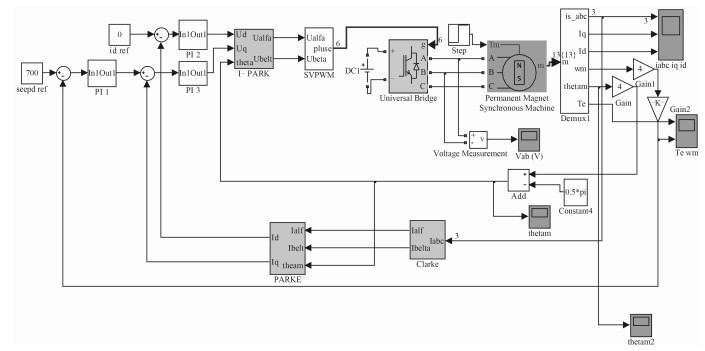
从图 1可看出,该控制系统采用双闭环控制,给定的参考转速是900 rpm;速度通过PI调节模块,实现转速的闭环控制策略,该调节采用输出限幅。接电流PI调节器模块构成电流的闭环控制,输出定子的电压dq轴分量ud 和uq ;I-park逆变器模块将两相旋转直角坐标系(dq)下的值向两相静止坐标系(αβ)下变化,它的输出是αβ轴的定子电压分量参考值Uα和Uβ;SVPWM和逆变模块用于实现参考电压逆变及其调制,从而可以直接通给电机;PMSM是永磁同步电机模块,负载转矩是模块Tm 。反馈通道模块为:Clark变换模块:实现三相坐标系(ABC)向两相静止坐标系(αβ)的转换,Parke变换模块:把两相静止坐标系(αβ)向两相旋转坐标系转换(dq),从而实现复杂电机参数的解耦。所谓的磁场定向控制就是把电机的三相电流转换为相互垂直的电流,而使其中一个电流为0[3]。这样通过控制另一个电流而控制电机的转矩,用传统直流电机的方法来控制交流电机,使得控制方法简单。
|
图 1 调速系统图 Fig. 1 Speed control system diagram |
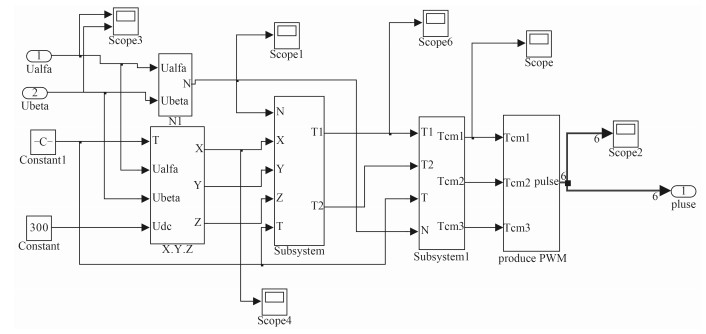
永磁同步电机中的相电流值呈现正弦波,所以相应的控制系统要求相电流也是正弦波,通过SVPWM来控制逆变器的6个功率管开合和关闭进而达到变频的目的。相应的构成模块有:扇区判断、XYZ计算、基本矢量时间分配、赋值模块及PWM波形产生(见图 2)。
|
图 2 SVPWM模块仿真图 Fig. 2 Simulation diagram of SVPWM module |
SVPWM模块通过Ipark变化输出值Ua ,Uβ 对逆变桥的6个功率管进行导通或者关闭来使得永磁同步电机的定子合成磁场与转子磁场相互作用[4]。
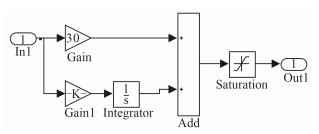
PID模块的结构如图 3所示:PID控制器工作机制是对闭环控制中误差信号进行响应,尝试对控制量进行调节,从而获得期望的系统响应。被控参数可以是任何可测量系统量,本系统中的被控参数是转速id 和iq 值[5],而实际使用时,由于考虑系统的相应速度在比例和积分参数介入的情况下已经满足要求,所以设计微分参数为0。
|
图 3 PI控制算法原理结构图 Fig. 3 Structure chart of conventional digital PI control algorithm |
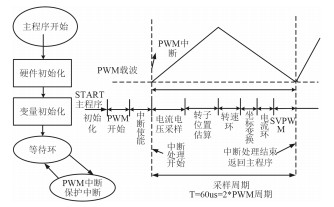
通过辅助工具ccs3.3,采用c代码编写控制程序,软件计时和总体框图如图 4所示。
|
图 4 软件总体流程图及计时时序 Fig. 4 Flow chart of software design and timing order |
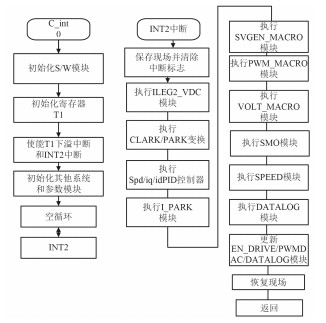
电动机控制的中断子程序是利用ePWM1作为中断源,时基是由一个PWM下溢中断的等待环(TBCTR=0x0000时产生事件),当定时器达到预设定时就会向CPU提出中断请求[6],当CPU响应中断时,对永磁同步电机控制的一系列程序就会执行[7]。在此程序中采用以速度环为外环、电流环为内环的双闭环控制系统,对电流和速度进行控制[8],其软件流程如图 5所示。
|
图 5 软件流程图(TMS320F281X系列) Fig. 5 Software flowchart (TMS320F281x series) |
解决的几个重要难点如下:
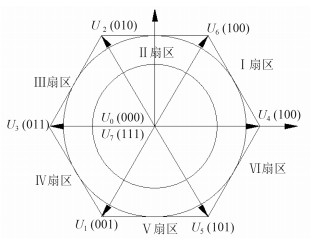
1)在SVPWM算法中把电机划分成6个扇区,并在算法中给了1个参数n,通过参数n就能知道电机合成磁场所在的扇区(见图 6)。参数n与扇区之间的关系见表 1 。
|
图 6 基本空间电压矢量图 Fig. 6 Basic voltage space vector |
|
|
表 1 SVPWM 计算的参数 n 与扇区关系 Tab.1 relationship between n and sector in SVPWM |
用手去旋转电机,会发现参数的变化是3,1,5,4,6,2依次重复,可以对应U3,U1,U5,U4,U6,U2。当电机在各种扇区时,会出现相应的比较值Ta ,Tb ,Tc 大于该比较值输出高电平,然后通过此来判断相应矢量的作用长度。动作输出高电平还是低电平由AQCTLA寄存器相应位来决定相应动作。在控制系统中取7500为计数器的最大值,TBCLK =2 × 7 500 × 1/150 μs=100 μs,f=10 kHz,其中150是dsp的频率PWM波形采用递增与递减格式,10 μs是isr这个中断进入的时间[9]。
| $ {T_1}{\rm{ }} = f \times 1 \; 000 \; 000 \times T/2{\text{,}} $ | (1) |
式中:T1为pwm.periodmax;T为周期,10 μs;f=10 kHz为时钟频率。
| $ {T_2}{\rm{ }} = {\rm{ }}\left( {f \times 200/\left( {30 \times 2} \right)} \right) \times 5\text{,} $ | (2) |
式中T2 为SYSTEM_FREQUENCY寄存器时间,用的是系统寄存器计时时间,当计数到0时,发生中断进入,时间是按照150 × 5 000/150 μs=5 000 μs,约为0.005 s时间。
2)电机初始角度即寻找电角度
如果多次实验证明电机的初始角度有问题,电机就无法平稳运行。控制系统采用12位的旋变,精度为1/4 096=0.000 244 140 6。由此可知该精度完全可以达到推进系统的要求。360°对应4 096,一个周期是6个sector,19对极电机1个电气周期对应的编码器是360/19=18.947°,属于一个扇区18.947/6=3.157 89°,对应的编码器是360°/4 096 × 3.157 89=36。电机的初始角度在36个编码器数值内变动,即:19对极,1个电气周期占的机械角360/19=18.95,1个sector占3.157 89°,对应12 bit为36。机械角度是P1-P0,P1是旋变反馈的当前位置数,P0是初始角度对应的编码,360°对应4 096输出,令X=(P1 -P0)/4 096,P3是电机当前编码器输出值,
| $ \begin{array}{l} P{\rm{ }} = \left( {{P_3} - {P_4}} \right) \times 0.00 024 414 06 \times 19{\text{,}}\\[5pt] 0.00 024 414 06 = 1/4096{\text{,}} \end{array} $ | (3) |
| $ \text{或} \quad P{\rm{ }} = {\rm{ }}\left( {4096 + {P_1} - {P_0}} \right) \times 0.00 024 414 06 \times 19{\text{。}} $ | (4) |
式(3)是电机正传时的值,式(4)是电机反转时的采样计算值。
电机初始角的确定方法,在SVPWMISR(void)中断函数中设置:
| $ \left\{ {\begin{array}{*{20}{c}} {{\rm{pwm1}}{.{\rm Mfunc} {C_1} = 1}}{\text{,}}\\[5pt] {{\rm{pwm1}}{{.{\rm Mfunc}} {C_2} = 0}{\rm{.5}}}{\text{,}}\\[5pt] {{\rm{pwm1}}{.{\rm Mfunc} {C_3} = 0}{\rm{.5}}}{\text{。}} \end{array}} \right. $ | (5) |
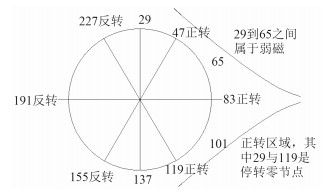
这样设定以后,给磁场一个固定的方向,让电机的电流从u相流进,vw相流出,此时给电机一个不大的电流,电机会被锁定在一个固定的位置,电流给定后用手去旋转电机的转轴[6],找出19个固定位置并读出相应的位置(19对极电机有19个初始角度),电机相应的会被锁定在19个位置,每个位置之间相隔36个编码数。通过实验发现电机的初始角如图 7所示:
|
图 7 电机初始角图 Fig. 7 initial angle of motor |
由图 7可知,1个电气周期对应的数是4 096/19=215.57,由6个扇区构成,一个扇区为35.929 8,首先看哪个扇区是正转,哪个扇区反转。再在正转的扇区,找稳定的初始角度。初始实验值从电机锁定的几个值对应的编码器值来选取[10]。选取不同的角度作为初始角,进行对比后最终选择出最合适的角度作初始角。
3)通过角度计算电机转速
| $ {{N_{speed}} = 200 \times 60n/360 = 33.333n}{\text{,}} $ | (6) |
在CCS中的程序是:
| $ {{{N}}_{{{Speed}}}}{\rm{ = DiffRotorAngle}} \times {\rm{33}}{\rm{.3}} {\rm{333}}{\text{,}} $ | (7) |
对电机转速进行滤波后:
| $ {{{N}}_{{{Speed}}}}{\rm{ = }}{{{N}}_{{{Speed}}}} \times 0.85 + {{{N}}_{{{Speed}}}} \times 0.15{\text{。}} $ | (8) |
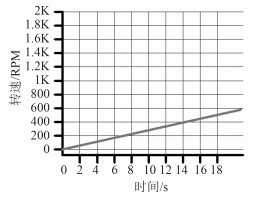
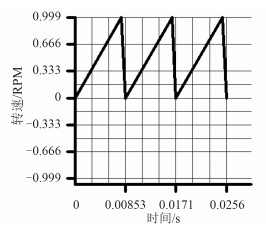
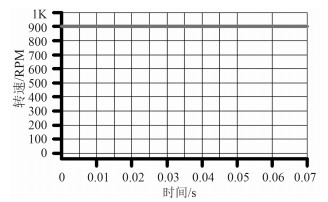
图 8是电机从零速启动, 图 9是电机的角度图,通过CCS中的DATALOG模块设置,就可以直接在CCS中绘图,图 10电机在900 rpm时的转速曲线,图 8~图11是通过实际的物理实验得到的真实数据,对相应电机进行Simulink仿真得到的数据进行对比。
|
图 8 电机零速启动图 Fig. 8 Motor starting speed wave |
|
图 9 电机角度图 Fig. 9 Motor angle wave |
|
图 10 电机900 rpm时的转速曲线 Fig. 10 Speed wave on 900 rpm |
|
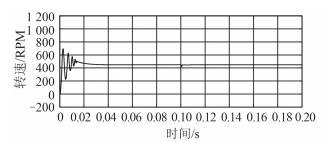
图 11 电机450 rpm的转速曲线 Fig. 11 Speed wave on 450 rpm |
|
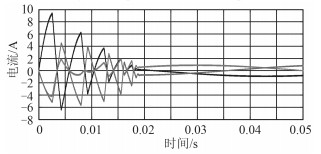
图 12 电机静止三相电流 Fig. 12 Motor's stator three phase current |
|
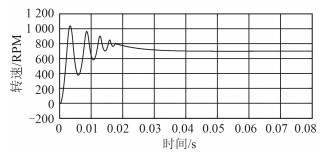
图 13 电机的速度曲线 Fig. 13 Motor's speed curve |
通过实验和Simulink仿真分析可知,电机有较好的动态性能,稳态运行波动小,对于UUV推进电机而言完全满足使用要求。
把工业中的控制方法运用在水下航行器同时用永磁同步电机提到直流电机做动力输入是本文的创新点,用更简单的方法寻找电机的初始角度并计算电机的转速,节省了编写复杂代码的时间,对于处理器而言节省了程序的存储空间,使得效率更高。
| [1] | 李刚. 数字信号微处理器的原理及其开发应用[M]. 天津: 天津大学出版社, 2000 : 239 . |
| [2] | 唐任远. 现代永磁电机--理论与设计[M]. 北京: 机械工业出版社, 1997 . |
| [3] | 李志民, 张遇杰. 同步电动机调速系统[M]. 北京: 机械工业出版社, 1996 . |
| [4] | 程善美, 蔡凯, 龚博. DSP在电气传动系统中的应用[M]. 北京: 机械工业出版社, 2009 . |
| [5] | MATSUI N. Sensorless PM brushless DC motor drives[J]. IEEE Transactions on Industrial Electronics , 1996, 43 (2) :300–308. DOI:10.1109/41.491354 |
| [6] | VAS P. Sensorless vector and direct torque control[M]. Oxford: Oxford University Press, 1998 : 122 -154. |
| [7] | LI L Y, CUI S M, ZHENG P, et al. Experimental study on a novel linear electromagnetic pumping unit[J]. IEEE Transactions on Magnetics , 2001, 37 (1) :219–222. DOI:10.1109/20.911825 |
| [8] | LI L Y, CUI S M, ZHENG P, et al. Experimental study on a novel linear electromagnetic pumping unit[J]. IEEE Transactions on Magnetics , 2001, 37 (1) :219–222. DOI:10.1109/20.911825 |
| [9] | HENKE M, GROTSTOLLEN H. Control of the NBP linear drive system[J]. Control Engineering Practice , 2002, 10 (9) :1029–1035. DOI:10.1016/S0967-0661(02)00039-4 |
| [10] | KANG D H, CHUN Y H, WEH H. Analysis and optimal design of transverse flux linear motor with PM excitation for railway traction[J]. IEE Proceedings-Electric Power Applications , 2003, 150 (4) :493–499. DOI:10.1049/ip-epa:20030191 |
 2016, Vol. 38
2016, Vol. 38
